形容朴素意在思维

●叶兴炎 (柯桥中学 浙江绍兴 312030)

形容朴素意在思维

●叶兴炎 (柯桥中学 浙江绍兴 312030)

2015年浙江省数学高考理科第18题考查函数的单调性与最值、不等式的性质.本题给人的第一感觉是抽象程度高、难度不小，但一经思考，就会发现其实只需讨论函数在区间［－1，1］的端点及对称轴处的取值情况，问题没有想象中的复杂;再仔细考虑，我们会发现该题解法很多，不同层次的学生都能找到适合自己的方法，不禁让人拍案叫绝.

题目已知函数f(x)=x2+ax+b(其中a，b∈R)，记M(a，b)是|f(x)|在区间［－1，1］上的最大值.

1)证明:当|a|≥2时，M(a，b)≥2;

2)当a，b满足M(a，b)≤2时，求|a|+|b|的最大值.

1 第1)小题的解法

1.1 分类讨论，最基础

当问题不能直接得到解决时，我们可以将问题分解成几个部分，然后对每一部分进行分析，从而得到整个问题的解决.这样处理从过程上看比较繁琐，但本质上是分类讨论的数学思想方法的运用，是学生应该掌握的基本解题方法.

解法1若a≥2，则，函数y=f(x)在x∈［－1，1］上单调递增.

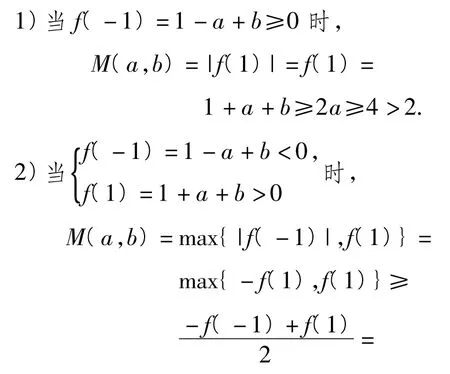
解法2由题意，得，从而|f(x)|在 x=－1或x=1处取到最大值，于是

1.2 几何意义，要掌握

|a|的几何意义是:数轴上表示a的点到原点的距离.解题时灵活地应用绝对值的几何意义，往往能使过程直观简洁，事半功倍.

解法3由题意，得，从而|f(x)|在 x=－1或x=1处取到最大值，于是

根据绝对值的几何意义，|b+1－a|+|b+1+a|表示数轴上的一点到－a和a的距离之和，则当这一点在－a和a之间取值时，|b+1－a|+|b+1+a|有最小值2|a|，因此

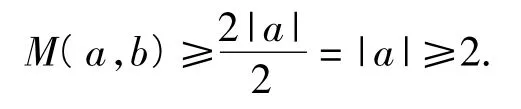
1.3 不等式性质，好想法

本题用不等式的相关性质就能解决.

解法4由题意，得，从而|f(x)|在 x=－1或x=1处取到最大值，于是

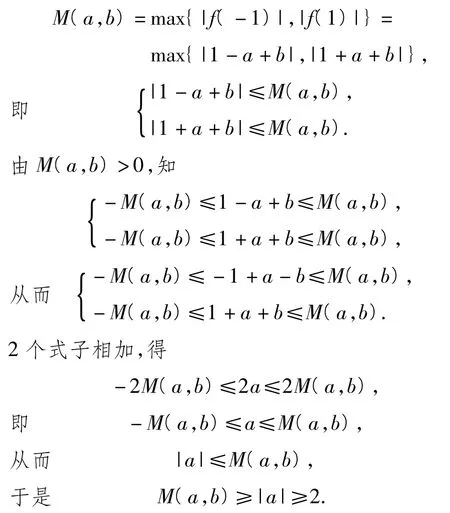
1.4 逆向考虑，新思路

根据题意，要证明的不等式“M(a，b)≥2”右边的“2”满足“2≤|a|”，a可以用f(1)，f(－1)表示，而f(1)，f(－1)与M(a，b)之间存在联系.

解法5由f(1)=1+a+b，f(－1)=1－a+ b，得

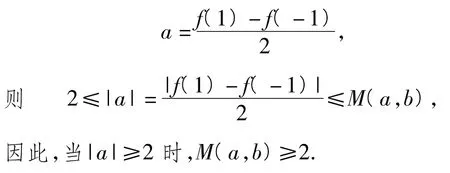
1.5 定理应用，很直接

应用绝对值不等式:若a，b∈R，则

本题可“秒杀”.

解法6由题意，得，从而|f(x)|在 x=－1或x=1处取到最大值，于是

2 第2)小题的解法

2.1 常规解法:线性规划

由M(a，b)≤2，可知|a|≤2，则|f(x)|在区间［－1，1］上的最大值在x=－1，x=1或处取到，从而

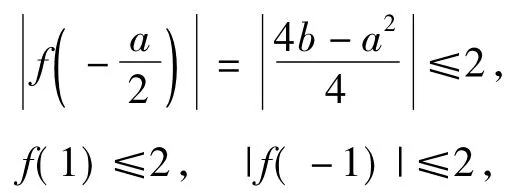
由此可画出可行域，原题转化为关于a，b的线性规划问题.从考后学生的反馈得知，这应该是最为普遍的做法.

解法1由M(a，b)≤2，可知|a|≤2，由题意可知|f(x)|在x=－1，x=1或处取到最大值，从而可行域为如图 1所示区域ABCD及其内部.令t=|a|+ |b|，则

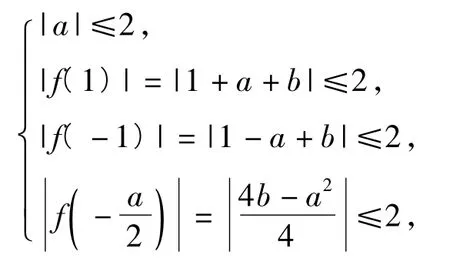
当b≥0时，b=－|a|+t，可行域为△AEF及其内部，从而当点(a，b)=(0，0)时，tmin=0，当点(a，b)=(0，1)时，tmax=1.

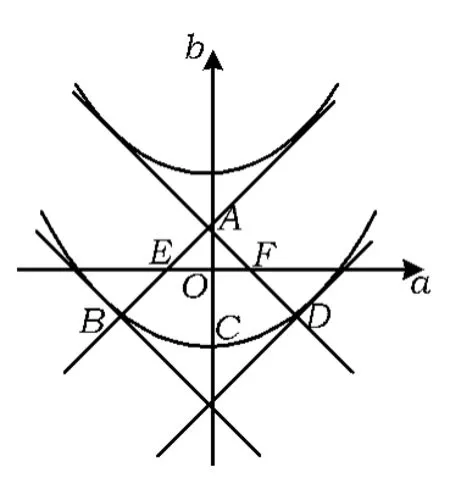
图1

当b≤0时，b=|a|－t，可行域为区域BCDFE及其内部，当点(a，b)=(0，0)时，tmin=0，当点(a，b)=(±2，－1)时，tmax=3.

综上所述，当a=±2，b=－1时，|a|+|b|的最大值为3.

2.2 巧妙手段:反解a，b

含绝对值的函数问题，我们可以对函数赋值，然后反解，用若干函数值表示a，b，转化为考虑函数性质的问题.

解法2由f(1)=1+a+b，f(－1)=1－a+ b，知

综上所述，当a=±2，b=－1时，|a|+|b|的最大值为3.

本题的命题背景简单、考查基础，从解法来看，第1)小题的解法除了绝对值不等式不作要求外，其他解法是常规的;而第2)小题的解法，也是学生应该掌握的，如果利用一些特殊的结论，过程就更简洁了.但为什么许多学生直呼被难倒了呢?笔者认为还是因为在教学中我们已习惯于把学生作为纯粹的解题机器，只顾着对学生进行知识的传授和灌输，忽视了对学生分析能力、钻研能力的培养，导致学生会解“面熟”的题目，但思维品质不高.高考试题恰有独创、新颖的特点，于是在考场上学生变得手足无措、无法快速找到问题的突破口.因此教师要理解新课改的理念，培养学生对数学学习的兴趣，教学中坚持以思维为本，辅以必要的教学指导和训练，使学生获得对高中数学知识本质和规律的掌握，提高高中数学教学的有效性.