管中窥豹可见一斑——2015年浙江省数学高考理科试题空间向量方法的启示

●沈国根 (湖州中学 浙江湖州 313000)

管中窥豹可见一斑
——2015年浙江省数学高考理科试题空间向量方法的启示

●沈国根 (湖州中学 浙江湖州 313000)

空间向量一直是中学数学的重要内容之一，历来是备考的重点复习对象.笔者通过对2015年浙江省数学高考理科试卷的深刻体验，发现有好几题都可以用空间向量的方法来进行求解、证明.这或许正是命题者从中想要贯彻的意图，以体现空间向量作为工具解决问题的重要性.下面笔者将自己的理解整理出来，以供参考.

1 例题赏析

例1如图1，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A'CD，所成二面角A'-CD-B的平面角为α，则

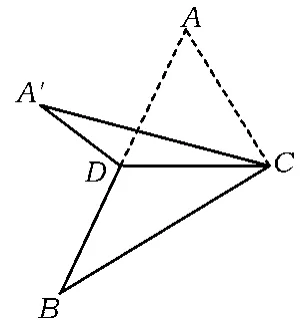
图1

( )

A.∠A'DB≤α

B.∠A'DB≥α

C.∠A'CB≤α D.∠A'CB≥α

(2015年浙江省数学高考理科试题第8题)

图2

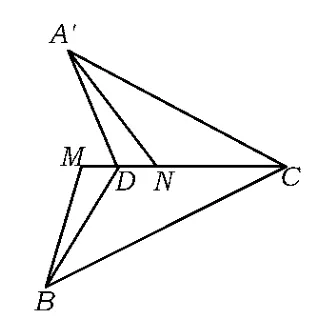
图3

解如图2，设∠ADC=β，∠CDB=γ，则β+ γ=π.如图3，设∠A'DB=θ，DA'=DB=t，DC=d.作A'N⊥DC于点N，BM⊥DC于点M，则

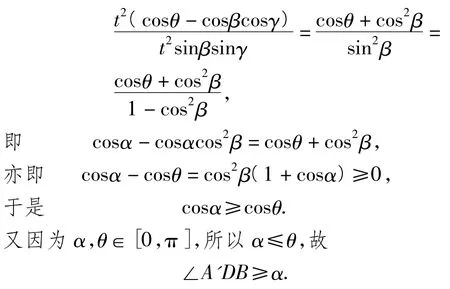
点评学生在实际解题过程中可能通过2个极端位置(2个半平面摊平和重合)来判断该题的答案.但只能做到知其然，不知其所以然.通过引入空间向量，可以很好地诠释这一动态过程.而且笔者发现，当D不是中点时，该结论也成立.

例2如图 4，三棱锥A-BCD中，AB=AC=BD= CD=3，AD=BC=2，点M，N分别是AD，BC的中点，则异面直线AN，CM所成角的余弦值是______.

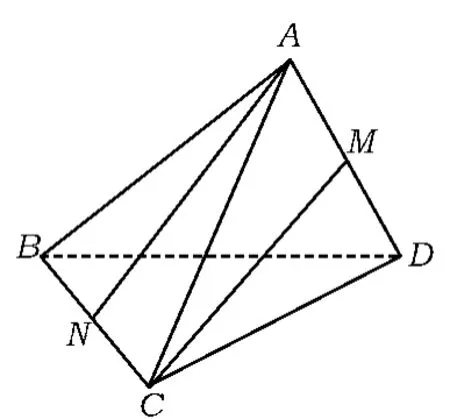
图4

(2015年浙江省数学高考理科试题第13题)

点评对于异面直线所成角的一般求法，都是通过空间问题平面化的思想，转化到某个三角形内进行求解.本题通过空间中2个向量所成角的思想，引入基底，不失为一种好方法.在基底的选择上，并不需要建构空间直角坐标系，而是选择了一组已知大小、夹角的基底.

例3已知e1，e2是空间单位向量，，若空间向量b满足b·e1=2，，且对于任意x，y∈R，|b－(xe1+ye2)|≥|b－(x0e1+ y0e2)|=1(其中x0，y0∈R)，则x0= ______，y0= ______，|b|=______.

(2015年浙江省数学高考理科试题第15题)

解如图5，把向量e1，e2，b共起点，记起点为O.对于任意x，y∈R，

(其中x0，y0∈R)，可得向量b的终点到 e1，e2确定的平面的距离为1，引入单位向量e3.记

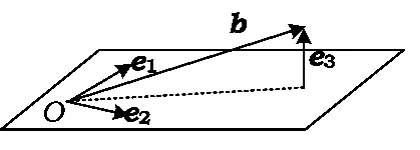
图5

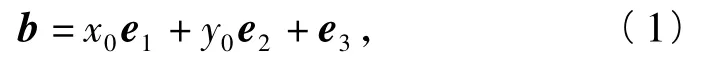
对式(1)的2边分别和e1，e2作数量积，可得方程组

点评对于该题的解法，笔者看到过好多种.但通过引入空间向量，却是最简单的解法.该题中，对于条件|b－(xe1+ye2)|≥|b－(x0e1+y0e2)|= 1(其中x0，y0∈R)的理解和把握是一个难点，这需要学生对向量加减法的几何含义有充分的认识.

例4如图 6，在三棱柱 ABC-A1B1C1中，∠BAC=90°，AB=AC=2，A1A=4，点A1在底面ABC的射影为BC的中点，D为B1C1的中点.

1)证明:A1D⊥平面A1BC;

2)求二面角A1-BD-B1的平面角的余弦值.

(2015年浙江省数学高考理科试题第17题)

1)略.

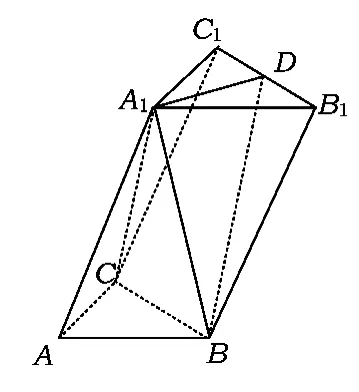
图6

图7

2)解以CB的中点E为原点，分别以射线EA，EB为x，y轴的正半轴，建立空间直角坐标系E-xyz(如图7所示).由题意知各点的坐标如下:

点评该题在解法上主要分2种:一种是传统意义上的点、线、面之间的位置关系;另一种就是用空间向量.但是对于空间向量，相当多的学生都是通过选择单位正交基底进行解题.其实，对于基底的选择并没有那么苛刻，只要满足通常意义上的有大小、夹角，都是不错的基底.例如，本题还可以选择为基底求解证明.

2 教学启示

高考试卷不但是对当年考生数学能力的考查，而且在一定层面上，也成为一线教师，特别是高三教师在数学复习过程中的一种导向.笔者认为，2015年浙江理科卷中的上述4道题，都能通过空间向量的方法来解决.这应该不是一种巧合，而是凸显了向量的思想、向量的方法在数学问题解决中的重要性.笔者有2点启示如下:

2.1 改变学生对空间向量方法的认识

在用空间向量解决立体几何问题的教学中，笔者深有体会:大多数教师都把墙角模式看得太重，高喊着“有墙角就用墙角，没墙角就挖墙脚“的口号，固化了学生的思维，使得学生一碰到立体几何的问题，就想方设法地建立空间直角坐标系，久而久之，把立体几何的教学变成了“解析几何”.其实，空间直角坐标系只是一组特殊的基底(单位正交基底)，而在基底的选择上，只要满足有大小、夹角，都可以构建起整个问题的向量计算体系.因此，要改变学生对空间向量体系的认识，不能是“我的眼里只有你”——单位正交基底.

2.2 重视教材中的课后习题

命题者与学生的共同财富是数学课本，试题以课本为基础，源于课本又高于课本.因此，在平时的教学复习中，应充分认识课本及课后习题的重要性，对于空间向量在立体几何中的应用，其实课本的课后练习及配套的《作业本》都有大量的空间向量方法，而且在习题的选择上，都凸显了对于一般化基底的应用.好好利用这部分练习，可以更好地提升学生在空间向量上的应用能力.