稳中求变体现创新——2015年浙江数学高考理科数列试题评析

●卢 明 (元济高级中学 浙江海盐 314300)

稳中求变体现创新
——2015年浙江数学高考理科数列试题评析

●卢 明 (元济高级中学 浙江海盐 314300)

2015年浙江省数学高考理科试题与前2年一样，考了一道数列解答题，分值为15分.不同的地方有2点:一是2015年理科数列增加了一个小题——选择题第3题，分值为5分，主要考查等差(等比)数列的概念、前n项和，解题思路常规，难度不高;二是数列解答题放在了第20题压轴题的位置，形式新颖，难度较大，学生普遍上手困难.这也是体现命题理念的一种创新——压轴题的第1)小题不再轻易送分，这一理念在2014年的压轴题上已经开始渗透.因为理科数列题的以上“新动向”，所以它自然成为大家关注和议论的热点之一.

2009年以来，浙江省数学高考理科试题都是以函数题压轴，多数是考导数知识，2014年考了带绝对值的函数.2015届高三是浙江省普通高中深化课程改革的第1届毕业生，数学教学内容有所调整，导数内容从“必修”变为“选修”，列入ⅠB范围.为此，高考前大家都在猜想:2015年浙江省数学高考理科压轴题将考什么?是延续2014年的考法?还是另辟蹊径?后来，坊间有传说，2015年理科数学可能会以数列题压轴.于是，“作为压轴题的数列又将会考什么?怎么考?”一线教师、教研员议论纷纷.各地模拟卷数列压轴题蜂拥而上，形式、内容、技巧各抒己见.为了让试题体现创新，凸显能力，命题者积极尝试与递推数列、不等式放缩等知识挂钩，各种题型层出不穷.

高考试题真的会是这样出吗?怎样做才能既达到“压轴”的目的，又不超越“课标”要求，还能坚守“宽入口、深展开、重通法、淡技巧”的浙江命题风格呢?这对命题者来说的确是一场严峻的挑战.然而，最终亮相的高考真题，还是较好地回答了以上问题.

1 试题再现，立意分析

例1 已知数列{an}满足，且(其中n∈N*).

(2015年浙江省数学高考理科试题第20题)

从试题表述看，它继续保持了简洁明了、通俗易懂的浙江风格，不让考生在审题上耗费过多的时间和精力.回顾2011～2014年的浙江省高考理科数列试题，不难发现，2015年的数列题与前几年相比，最明显的差异在于已知条件发生了质的变化:条件给出的数列{an}既不是等差数列，也不是等比数列，而是一个递推数列，并且它的递推关系也不是学生常见的;从求解的结论看，摆脱了以往求通项、求和之类的常规设问，而是将数列与不等式证明结合起来，后面的“尾巴”翘得也比较高，压轴压得很稳当.要说继承，2011年考过2个数列的和比大小，2014年考过不等式恒成立问题，因此2015年考不等式证明，不是空穴来风，而是一种继承和发展.用数列题代替函数题压轴，是2015年命题布局上的一种创新.

2 解法探讨，智慧碰撞

例1入口虽宽，但门槛较高，加上条件表述方式比较新颖、隐蔽，导致考生难以上手.首先，许多考生对递推关系中的，没有读懂所蕴含的意思，从而没有想到判断数列{an}的单调性.有的考生证明了{an}单调递减，但是没有意识到需要证明an＞0，或者无法证明，导致解题漏洞.下面解答例1.

先证例1的第1)小题.

证法1由题意，知数列{an}单调递减，且

由式(1)得

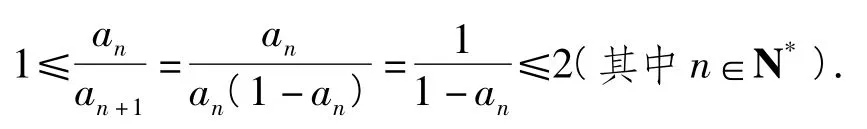
(注:以上是命题组给出的证法.)

证法2先证.数列{an}的单调性及an＞ 0(其中n∈N*)的证明同“证法1”.由式(1)得an+1≤ an，所以.

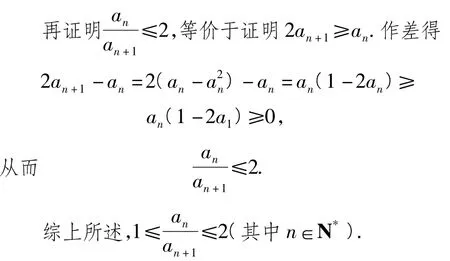
点评“解法1”中证明数列{an}单调递减用的是作差比较法，即先证an+1－an≤0.也可以直接用放缩法来证，即，进而有.

以上证明中，由式(1)得不出an＞0，因此要往下证，必须先证明an＞0，否则，在不等式an+1≤an的2边同除以an+1时就会有问题，这一点考生往往容易疏忽.有多位学生在第1)小题的证明中产生了类似错误，如:

证明an≠0还可以使用反证法.证法如下:

假设an=0.由已知得，因为，所以an－1=0.由递推式得an－1=an－2=…=a1=0，矛盾，从而an≠0.

点评例1第1)小题考查的知识点和思想方法主要有递推数列、数列的单调性、不等式的基本性质、作差比较法以及等价转换的数学思想.

下面证明例1的第2)小题.

证法1由条件得

点评以上证明使用了迭代法、分析综合法和放缩法，不少学生用了以上方法，有的教师认为本题有“超纲”的嫌疑.

再来看看命题组给出的解法.

证法2式(3)之前的证明同“证法1”.式(3)之后的证明如下:

命题组的证法没有使用放缩法，只是利用了第1)小题的结论和递推关系，然后使用“同向不等式相加”等不等式基本性质.关于本题所考查的知识点，命题组的说法是:“主要考查数列的递推公式与单调性、不等式性质等基础知识，同时考查推理论证能力.”

此题还可以用数学归纳法来证明.

3 命题反思，观点探讨

3.1 标准研读

鉴于有不少教师认为例1超纲，笔者仔细研读了《2015年浙江省普通高中考试说明》(下称《考试说明》).《考试说明》中对“不等式”的考试要求是:会从实际情境中抽象出一元二次不等式模型;了解一元二次不等式与相应的二次函数、一元二次方程的联系;会解一元二次不等式.会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组;会从实际情境中抽象出一些简单的二元线性规划问题，并能解决.会用基本不等式(其中a≥0，b≥0)解决简单的最大(小)值问题.《考试说明》中确实没有提及“不等式的基本性质”.笔者又查了适合2015届学生的《浙江省普通高中学科教学指导意见》(2012版)(下称《学科指导意见》)，对不等式的基本性质的要求是:理解并掌握不等式的基本性质，能利用不等式的性质比较两数(式)的大小，并证明一些简单的不等式.对不等式证明的要求是:了解比较法、综合法、分析法、反证法和放缩法，并能利用它们证明不等式.

3.2 “两度”追思

所谓“两度”，即试卷的“效度”与“信度”.“效度”是指所测量到的结果反映所想要检测内容的程度.“信度”是指测验得到的结果的一致性、稳定性及可靠性.简单地说，“效度”要靠试题所考查的知识点来保证，“信度”要靠考查相同知识点的试题的数量来保证.

数列应该考什么?《考试说明》对数列的考试要求是:理解等差数列、等比数列的概念;掌握等差数列、等比数列的通项公式与前n项和公式;了解等差数列与一次函数、等比数列与指数函数的关系;能利用等差、等比数列前n项和公式及其性质求一些特殊数列的和;能运用数列的等差关系或等比关系解决实际问题.回顾近5年的浙江理科数学卷，数列题所考查的知识点都能紧扣《考试说明》的要求.2015年的理科数列题有一大、一小2道题，共计19分.其中第3题考查的是数列的核心知识，符合《考试说明》，但试题简单，区分度较低;第20题真正考查《考试说明》要求的数列核心知识的只有第2)小题中“求和”一步，分值为3分，与第3题合计分值为8分，其他分值是在考查《考试说明》以外的数列与不等式知识.尽管高考强调在知识的交汇处命题，但是，笔者认为这种交汇应该限定在《考试说明》的范围之内.

3.3 试题赏析

下面的试题来自2015年有关地市模考试卷的压轴题，让我们一起来鉴赏一下.

例2已知数列{an}的前n项和为Sn，且满足3Sn=an－1(其中n∈N*).

1)求数列{an}的通项公式;

分析1)由条件推得

点评本题主要考查数列“和与项”的关系，等比数列的通项、前n项和以及指数运算.通项变形时有涉及到放缩，但是放缩的目的明确，技巧要求合理，放缩后可将数列转化为等比数列求和.一般情况下，若经过简单放缩能将一个复杂的求和问题转化为“等比数列求和”或“裂项求和”，则属于通性通法.笔者认为，本题还是符合“课标”要求的.

本题通项bn还可以采用以下放缩方法，实现异曲同工的效果.

点评本题主要考查数列“和与项”的关系，等差数列的定义及通项、放缩法、裂项求和法，同时考查学生的分析、综合和预见能力.本题的放缩虽然不是一步到位，但是入口较宽，学生经过尝试，容易找到突破口.本题的难点是形如的分式如何“裂项”，这需要经验的积累，也需要有一定的预见性，要求比较高.

以上试题的共同特点:第1)小题起点适中，尽管每题的第2)小题都有放缩，但是对放缩的技巧要求掌控较好，更重要的是每题对数列核心知识的考查都能紧扣《考试说明》的要求，而且分值占比合理，也能体现在知识的交汇处命题的特点.

4 启迪感悟，教学建议

毋庸置疑，《考试说明》对高中教学起着重要的导向作用.但是高中教育也不仅仅是为了高考，不能太功利，不要忘了基础教育是为学生的人生奠基这一神圣的使命.

4.1 基于“标准”教学

所谓“标准”，即高中数学课程标准，它是国家高中数学课程教学的指导性文件，关系到高中数学课程育人的价值取向和学科三维目标的落实.对浙江省来说，“标准”就是基于《国家高中数学课程标准》制定的《浙江省高中数学学科教学指导意见》.只有坚持基于“标准”教学，才能夯实基础，培养能力;才能优化育人模式，让学生感受学习的快乐.这是对学生负责，也是深化课程改革之必须.

4.2 把握“核心知识”

要想把握“核心知识”，必须对“标准”进行认真解读.“解读”的要义不在“读”，而在“解”.何谓“解”?就是要读懂文字背后的意思，即“标准”所述的“核心知识”的外延.鉴于数学学科的特点，数学核心知识包括基础知识、基本技能、基本方法和基本数学思想.高考命题就是考《考试说明》要求的“核心知识”.教师还要把握“标准”难点，即把握它的“外延”，不断地学习，不断地积累，不断地“悟得”.

4.3 提高解题能力

解题能力是数学教学应该着力培养的一种能力.一名学生数学知识会不会，思维水平高不高，数学能力强不强，都可以通过解题来反映.数学高考就是通过多个数学题的解答来检测学生对基础知识、基本技能的掌握情况，同时检测学生的思维能力和学科思想的运用能力.当下的数学高考，许多试题还强调在知识的交汇处命题，以考查学生的迁移能力、分析综合能力和解决实际问题的能力.因此，提高学生的解题能力，在平时教学中要注意加强知识的纵横联系，帮助学生构建合理的知识结构与知识系统，提高学生在新问题情境下准确把握核心知识、形成解题决策的能力.要切实解决好学生“假懂、疑似懂、似懂非懂”的问题，即“懂而不会”、“会而不懂”.所谓“懂而不会”是指能够听懂教师所讲的内容，但是不会灵活应用，表现在解题时没有思路、不会做，或做不对、做不全.“会而不懂”是指表面上会做相关的题目，但是本质上没有理解和掌握，具体表现在2个方面:一是客观题结果正确，但是思维过程错误;有的正确结果是用特殊代替一般，连猜带蒙得到的.二是解答题过程和结果虽然正确，但是只停留在简单模仿的层次上，没有真正理解解题的思路和方法，不能实现有效的迁移.要解决以上问题，教学中应尽量让学生多交流，从个人的表达与对话中发现他们在解题过程中出现“懂而不会”和“会而不懂”现象的原因，对症下药，采取措施，逐步消除上述现象，提高他们的解题能力.

总之，学得会，考得好，是每一个教师、学生的共同愿望，如果能坚持做到以上几点，那么我们的愿望就能成为现实.