识得棱锥真面目 只缘身在立体中——利用长方体视角解决几类常见的棱锥模型

●顾予恒 朱成万 (杭州第十四中学 浙江杭州 310006)

识得棱锥真面目 只缘身在立体中
——利用长方体视角解决几类常见的棱锥模型

●顾予恒 朱成万 (杭州第十四中学 浙江杭州 310006)

2015年的高考大幕徐徐落下，纵观各地数学高考试题，立体几何的相关问题大都有三小一大，分值占到了卷面的，特别是立体几何的小题往往成为学生眼中最惧怕且失分最多的问题之一.究其原因，立体几何对于学生空间想象能力的要求较高，对几何思维考查的难度较大.空间向量工具的引入，一度使得立体几何空间想象能力较弱的学生看到了解题的曙光.立体几何大题一般比较容易通过建系转化为坐标代数运算解决，但小题的建系就比较困难或者费时费力，因此让学生熟练掌握几类常见模型，能在第一时间洞穿题中的几何体来自何方，是解决立体几何问题的有效途径.

本文结合各地数学高考真题与模拟题，为大家介绍“全等体”、“三截棍体”、“鳖臑体”、“墙角体”等几种常见棱锥模型，供大家参考.

1 引子

在作业本中有这样的一道习题:

例1在正方体上任意选择4个顶点，它们可能是如下各种几何体的4个顶点，这些几何体可以是______(写出所有正确结论的序号).

①每个面都是全等三角形的四面体;

②每个面都是直角三角形的四面体;

③有3个面为直角三角形的四面体.

图1

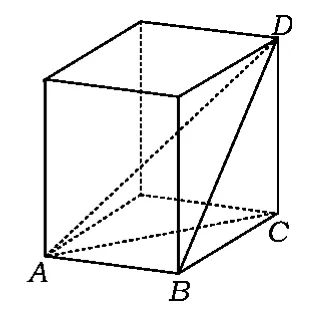
图2

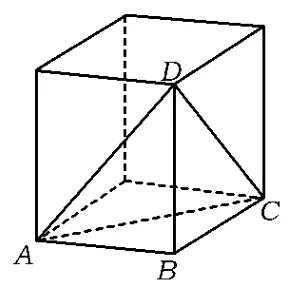
图3

图4

分析本题的答案是①②③，如图1～4所示.这里将4种常见的三棱锥放入到了外接的立方体中，有助于在立方体中更好地探寻棱锥的性质.

立体几何问题总是以各种棱锥(柱)作为载体，考查线线、线面与面面的位置关系及角度、长度、面积、体积的计算.而各种棱锥(柱)都可以由一个外接的长方体切割而成，因此找到对应的外接长方体(立方体)，就犹如搭好了脚手架，让问题的解决变得一目了然，正所谓“识得棱锥真面目，只缘身在立体中”.

2 全等体——每个面全等的四面体

如图1，将四面体放入长方体中，注意到三棱锥是由长方体的6条面对角线组成，可以很容易发现它具有以下性质:

性质1)四面体的3组对棱分别相等，即AB=CD，AC=BD，AD=BC;

2)四面体的4个面全等;

3)从四面体ABCD每个顶点出发的3条棱两两夹角之和为定值;

4)从四面体ABCD每个顶点出发的3条棱的长可作为一个三角形的3条边长;

5)连接四面体ABCD每组对棱中点的线段相互垂直平分.

分析1)将四面体ABCD放入长方体中，它的3组对棱恰好为长方体的3组面对角线，因为长方体对棱相等，所以性质1)显然成立.特别地，当所有棱都相等时，就是放在正方体内的正四面体.

2)我们还可以发现，这个四面体每个面的三角形都由长方体不同的3条面对角线构成，因此根据“SSS”全等的判定法则，性质2)也成立.

3)由性质2)可知，从四面体ABCD每个顶点出发的3条棱两两夹角恰好是四面体一个面三角形的3个内角，和为定值.

性质4)和性质5)利用长方体的视角来审视，也是显而易见的.

这些性质恰好是由2012年安徽省数学高考试题第15题演变而来，同时提供了一个非常有用的模型——全等体.凡遇到描述为对棱相等、四面全等、正四面体的四面体都可以放入长方体内，在长方体内重新解读题目的含义.

例2如图5，在三棱锥A-BCD中，AB=AC= BD=CD=3，AD=BC=2，若M，N分别为AD，BC的中点，则异面直线AN，CN 所成角的余弦值为______.

(2015年浙江省数学高考理科试题第13题)

分析本题可以有多种解法，但若注意到三棱锥3组对边两两相等，就可以将其放入长方体内，构造长方体模型“秒杀”.

如图5所示，根据题中条件AB=AC=BD=CD=3，AD=BC=2，可得构造的长方体长、宽、高分别为.

图5

解法2如图6构建了长方体，用几何法解决也是易如反掌.联结 ME，显然ME∥AN，故所求角即为∠CME.因为

图6

本题与2015年浙江省杭州市高三二模理科第13题有异曲同工之妙.

例3在正四面体ABCD中，M是AB的中点，N是棱CD上的一个动点.若直线MN与BD所成角为α，则cosα的取值范围是______.

(2015年浙江省杭州市高三二模理科试题第13题)

分析因为ABCD是正四面体，所以可以构建如图7所示的外接正方体.

以O为原点、OD为x轴、OC为y轴、OA为z轴建立坐标系，则A(0，0，2)，B(2，2，2)，C(0，2，0)，D(2，0，0)，M(1，1，2)，N(x，2－x，0)，故

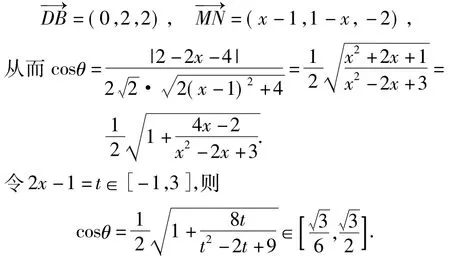
图7

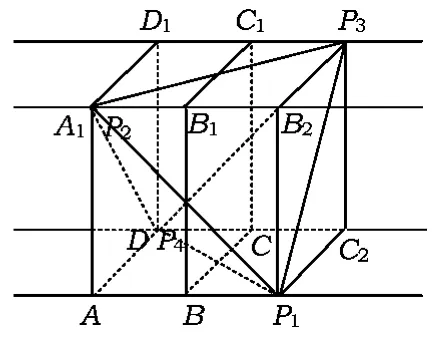
图8

浙江省历年高考题中也多次出现这一模型，例如:

例4在长方体 ABCD-A1B1C1D1中，AB=1，AD=2.若存在各棱长均相等的四面体P1P2P3P4，其中P1，P2，P3，P4分别在直线AB，A1B1，C1D1，CD上，则此长方体的体积为______.

(2014年浙江省数学高考样卷第17题)

分析本题可以理解为在一个截面为AA1D1D，且2端延伸的长方体通道内找一个内接正四面体P1P2P3P4，故只需保证长方体通道内能够放入一个棱长为2的内接正方体即可.如图8，取点P1，P2，P3，P4，可知长方体的高为AA1=AD=2，故长方体的体积为1×2×2=4.

3 三截棍体、鳖臑体——有4个面为直角三角形的四面体

如图2，我们注意到三棱锥D-ABC的4个面全是直角三角形，且3条棱DC，CB，BA首尾相接，两两垂直，恰好为外接立方体中对应长、宽、高的3条棱，故可以将“4个面都是直角三角形的三棱锥”形象地称为“三截棍体”(如图9).笔者上课讲解时联系周杰伦的成名曲《双截棍》，有助于学生的理解与记忆.

2015年湖北省数学高考卷中有一段摘自《九章算术》的文字，“将四个面都为直角三角形的四面体称之为鳖臑(拼音biē nào)”，这一个与“别闹”同音的词一时成为新闻媒体的热点词汇，大家都在调侃数学原来可以这么有文化.相信这一趣闻对学生的记忆会很有帮助，将来也可以称为“鳖臑体”.

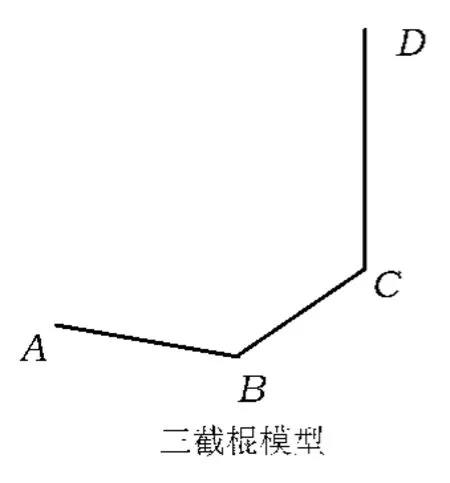
图9

图10

例5《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将4个面都为直角三角形的四面体称之为鳖臑.

如图10，在阳马P-ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，联结DE，DF，BD，BE.

1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑?若是，写出每个面的直角(只需写出结论);若不是，说明理由.

(2015年湖北省数学高考理科试题第19题)

分析本题首先证明“DE⊥平面PBC”，目标指向明确，只要找到2组线线垂直即可，同时也为第2)小题提供铺垫.判断四面体EBCD是否为鳖臑，即判断四面体EBCD的4个面是否全是直角三角形.如果从三截棍体的角度出发，只要找到首尾相接的3段两两垂直的线段即可.显然图10中DE，EC，CB首尾相接且两两垂直，故四面体EBCD是鳖臑，其中∠DEC=∠DEB=∠ECB=∠DCB=90°.

例6如图11，三棱锥P-ABC中，PA⊥平面ABC，PA=1，AB=1，AC=2，∠BAC=60°.

1)求三棱锥P-ABC的体积;

(2015年安徽省数学高考文科试题第19题)

分析本题中由AB=1，AC=2，∠BAC=60°可得AB⊥BC，又由PA⊥平面ABC，可知三棱锥P-ABC是一个三截棍体，可以放入长方体内，便于建立坐标系设点，同时几何方法也更容易发现添辅助线的方法.

图11

图12

本方法的辅助线添法实际是过点B作AC的垂面BMN与PC的交点即为所要求的点M.

例7已知球O的面上有4个点A，B，C，D，DA⊥平面ABC，AB⊥BC，，则球O的体积等于______.

(2008年浙江省数学高考理科试题第14题)

分析由题意可知，三棱锥D-ABC是一个“鳖臑体”.如图13，以DA，AB，BC为棱长构造正方体，设正方体的外接球球O的半径为R，则正方体的体对角线长即为球O的直径，从而，于是，故球O的体积.

图13

4 墙角体——有3个面为直角三角形的四面体

如图3，三棱锥D-ABC的3个面是直角三角形，点B处恰好是一个3条棱两两垂直的墙角，故这样的三棱锥可称为“墙角三棱锥”.墙角体是立体几何用向量方法解决问题的根本模型，有了墙角也就有了直角坐标系，因此遇到描述为“3个面为直角三角形”的四面体就可以放入长方体(即直角坐标系)内(如图3和图4)研究问题了.

例8已知三棱锥A-BCD的外接球为球O，△ABC与△ACD都是以AC为斜边的直角三角形，△BCD是以BD为斜边的等腰直角三角形，且，向量的夹角为，则球O的表面积为______.

分析因为这个三棱锥有3个直角三角形，所以可以将其放入如图4所示的长方体内，则由，可知BC=CD=1.又由于，从而△ABD是正三角形，长方体的高为1，即这是一个正方体.故三棱锥的外接球与正方体的外接球相同，从而正方体的体对角线就是球O的直径，故球O的表面积为3π.

例9有2块直角三角板:一块三角板的2条直角边的长分别为;另一块三角板的2条直角边的长分别为.这2块三角板有2对顶点重合，且成90°的二面角，则不重合的2个顶点间的距离等于______.

分析这里有众多的直角三角形，故考虑2块直角三角板拼成的三棱锥可能有2种拼接方式:一种拼成墙角三棱锥，一种拼成“三截棍体”三棱锥.

若是墙角三棱锥，则

从而△PAQ为直角三角形，于是

若是三截棍体三棱锥，则

例10如图14，某人在垂直水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角)，若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值为______.

(2014年浙江省数学高考理科试题第17题)

分析本题的常规做法是将仰角正切值表示成为函数求值域.但是若将三棱锥P-ABC放入长方体内，则可以“秒杀”这个问题.

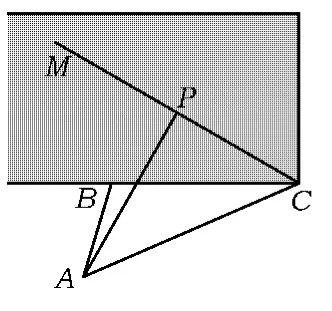
图14

图15

如图15，构造长方体，则AP和面ABC所成最大的角即为面ACD和面ABC所成二面角.易知面ACD和面ABC所成二面角的平面角为∠DFB，故

在日常教学中我们发现，学生惧怕立体几何问题，其主要原因往往是因为无法将题中所给的抽象条件转变为直观图像.因此为各式各样的棱锥构建外接长方体的脚手架，可以使得这些棱锥更有“大局观”，更易于学生亲近和熟悉.例如2条异面直线垂直未必人人都能一眼望穿，但如果这2条异面直线恰好能作为正方体的面对角线，那么学生对于垂直这一性质的敏感度就会大大提升.因此作为一线教师，在讲授立体几何内容时，应注意和学生一起发现、探究立体几何图形的出处，这样既有助于学生空间位置感觉的提升，也能加强学生的建模化归能力，真正收到“解一题，通一类”的效果，帮助学生看穿这纷扰的立体世界.

［1］吴文尧.活跃在立体几何高考题中的明星四面体［J］.中学教研(数学)，2014(8):32-34.