能力立意呼唤教学回归——2015年浙江省数学高考试卷评析

●郑日锋 (学军中学 浙江杭州 310012)

能力立意呼唤教学回归
——2015年浙江省数学高考试卷评析

●郑日锋 (学军中学 浙江杭州 310012)

为了有利于高校选拔合格新生，有利于中学数学教学改革，高考命题实现从知识立意到能力立意的转变，而真正贯彻这一原则的数学高考试卷却凤毛麟角.我们欣喜地看到了2015年浙江省数学高考试题，命题专家为我们设计了一份“清新自然”、“立意高远”、体现能力立意的试卷，其中许多题目“余音绕梁，回味无穷”.然而考后考生、教师一片异议，认为这是浙江省高考史上最难的试卷，这究竟是什么原因呢?高考与教学有着怎样的关联?本文阐述2015年浙江省数学高考试题中的各种类型问题的特点及教学导向.

1 基础题——注重理解

试题立足教材而不拘泥于教材，平和朴实，内涵深刻，给人以“题在书外、根在书中”的感觉，如理科卷第1，2，3，4，9，10，11，12道题(占42分)，文科卷第1，2，3，4，9，10，11，12道题(占44分)都是基础题，考查基础知识和基本技能.这些题目起点较低，考查的知识点比较单一.解决这些题目需要理解教材中的相关概念，掌握基本技能.

2 常规题——注重方法

试卷注重通性通法，注重对数学思想方法的考查，如理科卷第5，13，16，17，19题(占53分)，文科卷第5，15，16，17，18题和第20题第1)小题(占60分)都是常规题.这些题目考查主干知识，考查多个知识点，题型熟悉，方法常规，入口易、宽，往往有多种方法.个别题目用不同方法解决问题所用的时间有较大的差异，考查多个知识点，在知识网络的交汇处命题，往往以知识为载体，考查数学思想方法及计算能力.解决这些题目需要认真审题，把握问题特征，合理选择方法.

例1如图1，已知椭圆上2个不同的点A，B关于直线对称.

图1

1)求实数 m的取值范围;

2)求△AOB面积的最大值(O为坐标原点).

(2015年浙江省数学高考理科试题第19题)

本题紧紧围绕用代数方法解决几何问题的核心思想，设计的问题也是解析几何中常规的弦长计算、垂直关系、求面积最值等常规问题，求解方法是解析几何中的常规方法，不在技巧上作文章，考查了数形结合思想、转化思想、函数与方程思想.

对于第1)小题，有以下2种解法.

解法1由题意知m≠0，可用韦达定理或“点差法”求出AB的中点P的坐标为，再由点P在椭圆内，得，从而实数m的取值范围为.

解法2由题意知m≠0，可用韦达定理或“点差法”求出AB的中点P的坐标为.直线AB的方程为

代入椭圆方程x2+2y2=2，得

因为直线AB与椭圆交于2个不同的点，所以

解法1技巧性较强，有些学生难以掌握，解法2属于通性通法，虽然它比解法1简便，但在解决第2)小题时，解法2显得苍白无力，而解法1却顺理成章.

应对常规题，在教学中做到以下几点是必要的:一是整合，归纳并总结各主干知识块的问题特征、解题策略、易错点、解题的误区.编织各内容的知识网络结构，按照知识、策略进行归纳，突出知识、策略间的联系及适用范围，这样做的目的是让知识与方法条理化、有序化、结构化，实现知识从厚到薄，达到“拎起来成条线，撒下来铺满地”的较高境界.二是突破，找准难点、重点、及薄弱环节，进行有针对性的训练，切忌盲目操练，重复操练.对于不太熟悉的方法，需引导学生有意识地运用它尝试解决相关问题.三是优化，引导学生学会从不同角度思考问题，从而开拓思路，优化思维.在复习课课堂上，教师要营造课堂氛围，给学生思考问题的时间与空间，培养学生的思维能力.

3 新颖题，注重本质

设计试题应尽可能多地从现实问题或几何背景出发，构造出素材朴实、内蕴丰富的试题，充分体现数学的内在实质.试卷中的题目处处闪现着问题解决的智慧.这样的试题，加强了对数学本质的考查，突出了对学生能力的考查.如理科卷第6，7，8，14，15，18，20题(占55分)，文科卷第6，7，8，13，14，19题和第20题第2)小题(占46分)，这些题目设计新颖，意蕴深邃，突出本质，考查考生的能力及数学素养.这类题目的比例比往年增加了不少，体现以能力立意的命题原则，通过不同的新颖题，比较全面地考查学生的能力.

1)阅读理解题.如理科卷第6题，这是一道阅读理解题，给出一种新的运算，然后研究此新运算的性质，判断2个命题的真假.解题时，需要考生理解新概念，然后在此基础上进行逻辑推理，利用数形结合思想解决问题，这样的考题真正考查了学生对数学问题的分析和理解能力，也说明了命题者匠心独运的价值取向.

2)形式化问题.如理科卷第15题，以长方体为背景，以空间向量为载体，问题给出了含有2个参数、2个独立变量及3个向量的不等式，实际上解决该问题可转化为点到平面的距离，利用2个向量垂直关系得到解决.文科卷第8题也属于此类问题.

3)应用型问题.如文科卷第7题:求粉刷房间的最低总费用问题，需要在6个代数式中找出最小值，实质上是排序不等式问题.

4)概念问题.彰显“数学在根本上是玩概念而不是玩技巧的”.

例2存在函数f(x)满足，对任意x∈R都有

( )

A.f(sin2x)=sinx B.f(sin2x)=x2+x

C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|

(2015年浙江省数学高考理科试题第7题)

本题考查函数的概念，函数是从定义域到值域的单值对应.对于选项A，取，得，取，得，不符合函数的定义，故排除选项A;同样可排除选项B和C;对于选项D，取函数，符合条件.

2015年浙江省数学高考文科试题第7题考查“圆、椭圆、双曲线、抛物线是圆锥面被不同位置的平面所截得的”这一知识点，需要考生具有较强的理解与转化的能力.

5)动态问题.

例3如图2，已知△ABC，D是AB的中点，沿直线 CD将△ACD折成△A'CD，所成二面角A'-CD-B的平面角为α，则 ( )

A.∠A'DB≤α B.∠A'DB≥α

C.∠A'CB≤α D.∠A'CB≥α

(2015年浙江省数学高考理科试题第8题)

图3

本题探索动态图形的不变性质，设置了一个弱条件(D是AB的中点)，其实点D可以是AB的其他分点.解决此问题可以利用特殊化思想，取锐角△ABC，当α=180°时，选项D不成立;当α=0°时，选项A，C均不成立.故选B.

选项B的正确性只要作出二面角的平面角，为此只需在原平面图形中，在CD取一点O作CD的垂线，变成空间图形后便成为二面角A'-CD-B的平面角α，归结为如下的数学模型:如图3，在四面体D-OA'B'中，DO⊥平面OA'B'，且OA'=OB'，则∠A'DB'≤∠A'OB'.

6)综合性问题.

例4设函数f(x)=x2+ax+b(其中a，b∈R).

2)已知函数f(x)在［－1，1］上存在零点，0≤b－2a≤1，求b的取值范围.

(2015年浙江省数学高考文科试题第20题)

本题是函数、方程、不等式的综合问题，第1)小题属常规题，解决第2)小题需要考生有灵活机智的解题策略及分析问题与解决问题的能力.下面仅给出第2)小题的解法.

解法1设s，t为方程f(x)=0的根，且－1≤t≤1，则

解法2由方程f(x)=0在［－1，1］上有实根及已知，得

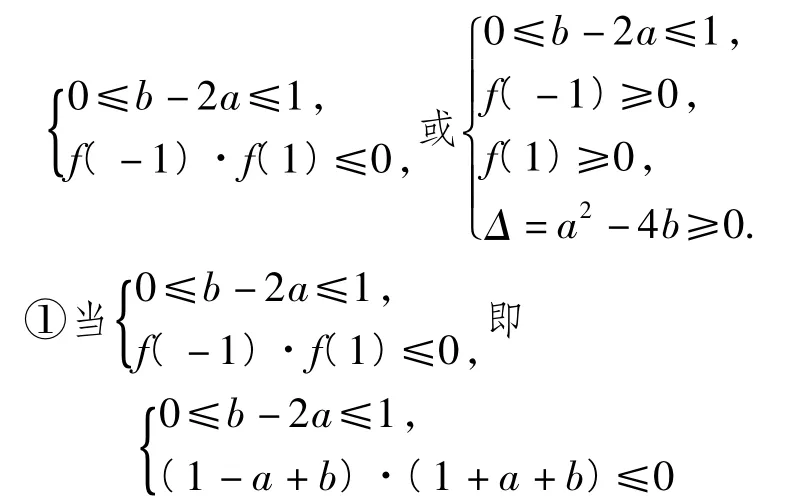
时，在坐标系aOb中作出点(a，b)的可行域如图4所示.由，D(－2，－3)，得.

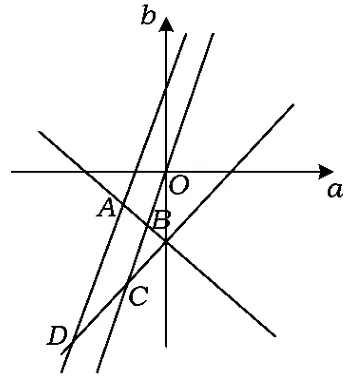
图4

图5

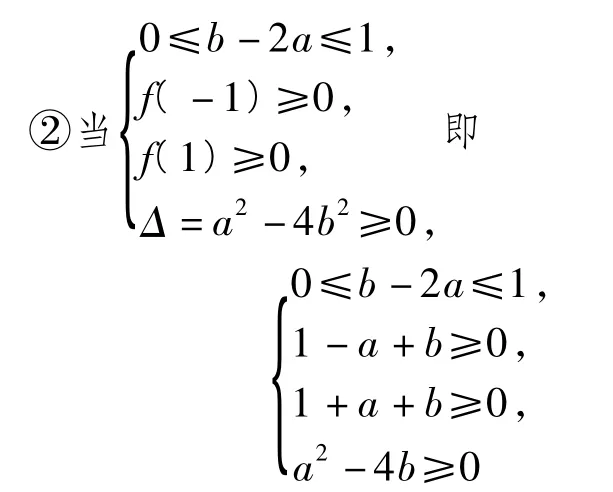
时，在坐标系aOb中作出点(a，b)的可行域如图5所示.由，得.

解法1为试卷提供的标准答案，在解题过程中，需要分别计算当0≤t≤1及 －1≤t＜0时，的取值范围，比较繁琐，而且忽略了方程有解对a，b的约束条件，有可能导致错误，欠严谨.解法2从形的角度出发，过程简洁，而且解法自然.分析与综合、归纳与演绎、具体与抽象等数学思想及基本逻辑方法在此题中均有很好地体现.此外理科卷第18，20题也属于此类问题.

从现实问题或几何背景出发，构造出素材朴实、内蕴丰富的新颖题，充分体现了数学的内在实质，试卷中的题目处处闪现着问题解决的智慧.只有会思考、具有良好思维品质与数学素养的考生才能得心应手.教师在教学中应重视一题多解和一题多变，在做中领悟，在做中提升，在做中研究，这样才能让学生在遇到新颖问题时运用所学知识去合理地展开联想、转换、探究.在复习中做适量的习题是必不可少的，但千万不能过量，依靠“题型+技巧 +大运动量训练”的教学应对新颖题是力不从心的;在复习中切实掌握数学思想方法，以不变应万变;开展探究式教学，引导学生建立数学模型，运用数学模型解题，提高学生的数学素养.

在2015届高三复习阶段，许多教师给学生做过如下题目:

例5已知函数f(x)=x2+ax+b(其中a，b∈R)的定义域为［－1，1］，记M为|f(x)|的最大值.

例6数列{an}满足(其中n∈N*)，则的整数部分是 ( )

A.1 B.2 C.3 D.4

例6为笔者所任教学校2015届高三最后一次适应性考试的选择压轴题，也是镇海中学的2013届高三最后一次适应性考试的选择压轴题.

例5以及2015年1月浙江省学业水平考试压轴题与理科卷的第18题是相关题，例6与理科卷的第20题是相关题，而且解题方法相类似.理科卷第18，20题是2015年理科试卷中师生评价最难的2道题，我们需要探讨的问题是:为什么学生做了例5、例6后，还是拿不下理科卷第18、20题?若教师能引导学生领悟这2道题的解题策略，尝试用多种方法解决，并且布置相关题目供学生练习，应该会有更多的学生做出这2道题.

结语高考试题总是在沿袭原来的命题风格的基础上适度创新，可谓稳中渐变，如果不改变教学策略，必然难以适应高考.我们的教学需要合理定位，应该清楚并不是所有的学生在高考中都可以拿高分，让不同层次的学生发挥出应有的较高水平，这才是我们的目标;搞“题海战术”不仅透支了学生未来对学习的兴趣，在高考中也不能取得理想的成绩，能力立意的高考试题呼唤教学回归教材，回归本质，回归学生.

［1］郑日锋，沈新权，蒋荣清.平淡中见灵动 细微处显意蕴——2012年浙江省高考数学试卷评析［J］.数学通报，2013(2):17-19.