团队断裂带计算理论综述

崔超，肖明，常乐

（北京科技大学东凌经济管理学院，北京 100083）

团队断裂带计算理论综述

崔超，肖明，常乐

（北京科技大学东凌经济管理学院，北京 100083）

团队断裂带是一条基于团队成员多个特征变量的虚拟的分割线，它将团体分割为内部均质、彼此异质的子团体。由于团队断裂带与团队绩效紧密相关，因此成为了研究高层管理团队绩效影响因素的新思路。本文回顾了多种断裂带计算方法，总结了各种方法的优势和局限性，并对未来断裂带研究的发展进行了展望。

团队断裂带；子团体；断裂带强度；断裂距离

1 引言

团队多样性研究一直以来都是人力资源领域的研究重点。虽然组织行为学界对团队多样性与绩效的关系以及影响机制进行了大量研究，但是并没得出一致性的结论。为此，学者提出研究多个特征变量同时作用对团队水平产出的影响。基于这种观点，Lau和Murnighan（1998）最先提出了断裂带（Team Faultlines）的概念。断裂带被定义为一条基于团队成员多个特征组合的虚拟的分割线，它将团队分割为内部相对同质、彼此异质的子团体，并对团队绩效产生影响。与多样性研究主要方法不同，断裂带是对多个多样性变量的组合同时进行研究。Lau和Murnighan（1998）提出的断裂带（Team Faultlines）概念是对团队成员特征多样性研究的深化，开辟了团队多样性研究新的领域。

团队断裂带普遍存在于社会各个团体中，其对团队绩效的影响也成为学者们研究的重点。Li和Hambrick（2005）和Knippenberg等（2011）的研究结果都显示，断裂带会对团队绩效产生消极的影响。为了对断裂带进行量化，学者们基于不同的断裂带理念，提出了多种衡量断裂带的方法，本文将对计算断裂带的主要方法进行总结与评述。

2 团队断裂带的研究方法综述

断裂带受团队成员个人特征的影响。这些特征一般可分为人口统计学特征和认知层面特征，前者包括性别、年龄、种族等特征，后者包括个性、价值观等特征。学者们围绕断裂带的检测和强度计算提出了不同的理论与方法。

2.1 Thatcher等（2003）的Fau值理论

Thatcher等（2003）提出了确定团队断裂带的方法，并给出了计算数值型断裂带强度Fau值的公式。假设某团队人数为n，将团队分割为两个子团体的所有可能方法数为杂=2n-1-1，对于分割方法早=1，2，…，S，Thatcher等使用特征变量子团体方差与总体方差的比值作为该断裂带的强度，用Faug表示，其计算公式为：

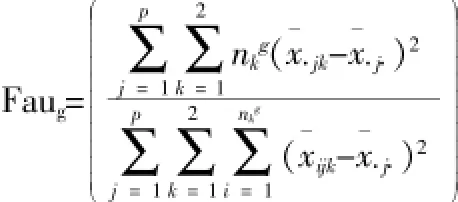
式中，p表示特征变量的数量，ngk表示第g中分割方法产生的子团体k中成员的数量，x·jk表示子团体k中特征变量j的均值，x·j·表示团k队总体特征变量j的均值，xijk表示子团体k中成员i特征变量j的值。在所有g种分割方法中，将计算得到的Faug的最大值作为该团体的断裂带强度，即Fau值。这种方法可以被看作是基于方差分析并强制分为两类的聚类分析方法。

Thatcher等（2003）的Fau值理论奠定了断裂带计算的基础，是使用最广泛的断裂带计算方法。Fau值理论使用数值型变量进行计算，得到数值型断裂带强度，方便了不同团体间断裂带强度的比较；通过计算能够确定团队成员与子团体的所属关系。为降低计算量，该方法将内部子团体数量限定为2个。

2.2 Gibson和Vermeulen（2003）的子团体强度理论

Gibson和Vermeulen（2003）提出了与断裂带概念相类似的子团体强度（Subgroup Strength）计算方法。他们认为，当团队内某些成员具有重叠而又与其他成员不同的人口统计学特征时，团队内部就会产生子团体。在这些子团体中内部成员的个人特征存在重叠，而在不同子团体成员之间个人特征很少或不存在重叠。子团体强度的计算公式如下：

式中，k是属性的数量，重叠度overlap载k，ij表示任意两个成员i和j之间属性k的重叠度。子团体强度为团队内任意两个人属性重叠度的标准差。重叠度可以通过使用连续变量和分类变量计算得到。例如，成员i和j均为中国人，则成员i和j的种族重叠度为1；若成员i为韩国人，成员j为日本人，则成员i和j的种族重叠度为0。对于连续变量，则使用两个成员属性的较小值与较大值的比值作为两成员该属性的重叠度。例如，若成员i年龄为40岁，工作经验为20年，成员j年龄为30岁，工作经验为10年，则二人的年龄重叠度为0.75，工作经验重叠度为0.5。因此，一般的分类变量的重叠度取值为0或1，连续变量的重叠度取值范围为0至1之间。

Gibson和Vermeulen（2003）的子团体强度理论使用数值变量进行计算，能够得到数值型的断裂带强度，并且适合子团体数量超过两个的情况，但是这种方法没有给出成员与子团体之间的所属关系。此外，由于重叠度不存在特定的取值范围，受所选取的特征变量的值的大小影响较大。

2.3 Shaw（2004）的FLS理论

Shaw（2004）测量了子团体内部分类变量的一致程度和子团体之间的差异。Shaw认为团队成员由于基于某一特定属性而形成子团体。Shaw将子团体内部成员在除特定属性外其他属性上的一致性变量称为内部一致性IA（the Internal Subgroup Alignment），与其他子团体在除特定属性外其他属性上的一致性称为跨团体一致性指数CGAI（The Cross-subgroup Alignment Index）。IA和CGAI指数取值范围均为0至1之间，断裂带强度数值FLS（Faultline Strength）的计算公式为：

FLS=IA×（1-CGAI）

由FLS的计算公式可知，断裂带强度FLS与IA指数呈正相关关系，与CGAI指数呈负相关关系。该方法使用分类数据进行计算，因此需要对连续性变量进行分类处理。例如按年龄将成员分为青年、中年和老年。但是在确定特征变量分类的数量和边界时，容易产生误差，例如青年、中年和老年的年龄划分边界是模糊的。计算得到的断裂带的强度FLS也会因对连续变量和认知层面的特征变量的分类数量和边界而产生误差。

Shaw（2004）的FLS方法是依据某个单一属性对团队成员进行分类的，因此每一属性下子团体的数量是由该属性类别的数量决定的。对计算中所涉及的所有特征变量，FLS方法无法确定成员与子团体固定的所属关系。

2.4 Li和Hambrick（2005）的派系断裂带理论

Li和Hambrick（2005）假设某一特定属性导致团队中产生派系，为研究该派系产生的断裂带强度，使用派系断裂带（Factional Faultlines）强度来衡量。Li和Hambrick按国籍将一家由美国公司和中国公司合并后的公司分割成美国派系和中国派系，然后计算了每个派系其他数值特征属性（如年龄、任期）的均值，并对团队内不同派系之间的差异进行了量化。Li和Hambrick计算得到了每个团队除国籍以外的其他人口统计学特征的d值。这些d值的和决定了给定团队派系断裂带的大小。

Li和Hambrick（2005）的派系断裂带理论研究了某一特定属性所导致的断裂带的强度，与Lau和Murnighan（1998）提出的断裂带概念有所不同。由于基于派系特征变量产生的断裂带的强度不一定是该团队内强度最大的断裂带，因此使用该方法计算得到的断裂带强度不能够完全代表团队内的断裂带情况。

2.5 Bezrukova等（2009）的断裂带距离理论

Bezrukova等（2009）认为在检测到最强断裂带后，断裂带的测量不仅应该反映团队成员特征变量的一致性程度（即断裂带强度），而且要反映子团体之间的距离，即断裂带距离（Faultline Distance）。他们认为断裂带的影响是断裂带强度和断裂带距离相互作用的结果。他们在文章中都提出使用Fau值理论检测最强的断裂带，在确定子团体划分后，将Fau值乘以子团体几何中心载和再的欧式距离阅e。

式中，xi表示一个子团体第i个多样性特征变量的均值，yi为另一子团体对应的特征变量的均值。团队内多个子团队的断裂带距离也可以通过计算得到，例如可以计算晕个子团体之间晕（晕-1）/2段距离的平均值。

2.6 Van Knippenberg等（2011）的多重相关系数方法

Van Knippenberg等（2011）提出了一种通过每一变量与其他变量的相关系数计算断裂带的方法。其计算断裂带强度Fk的公式为：

式中，k为选取的特征变量，Rxi，｛Allx≠xi｝为变量xi与其他变量的多重相关系数。

Van Knippenberg等（2011）的多重相关系数方法适合计算连续变化的属性变量且计算量较小。这种方法没有给出子团体的数量和成员与子团体的所属关系。此外，由于在计算各特征变量的相关系数时Rxi，｛Allx≠xi｝每个特征变量都作为回归方程的因变量，因此无法有效计算某一属性完全相同的团体的断裂带强度。例如在研究涉及学历的断裂带时，若团体内所有成员学历相同，即使团队中存在一些重叠的其他属性特征，计算得到的断裂带强度仍然为0。

2.7 Lawrence等（2011）的潜聚类模型

Lawrence等（2011）使用潜聚类方法对断裂带进行了计算。每个团队成员通过其归属某一特定类的后验概率来决定其所归属的子团体。由于在均质的类中其后验概率较高，因此团队所有成员后验概率的同质性可以被用来衡量断裂带强度。由于使用不同的聚类方法对团体内成员进行聚类，得到的子团体数量是不同的，因此之后需要使用贝叶斯信息准则（BIC）确定最佳分割方法。

3 分析与展望

目前应用最广泛的断裂带计算方法是Thatcher等（2003）的Fau值理论，结合Bezrukova等（2009）的断裂带距离理论，能够得到比较客观的断裂带强度值。但是断裂带距离理论是基于断裂带强度和距离正交的基础之上的，而计算Fau值时断裂带强度和距离存在一定相关性，所以将Fau值与阅e值相乘的计算结果与真实值存在一定偏差。

此外，常用的方法还有FLS理论和潜聚类方法。FLS理论计算断裂带强度需要把连续变量转变为分类变量，结果受特征变量数量和它们的分类数量影响较大。潜聚类方法是一种使用较晚但是潜力巨大的计算断裂带的方法。它降低了Fau值理论在不限制子团体数量时巨大的计算量，能够识别两个以上的子团体，并能够得到成员与子团体之间的所属关系。

对于团队中产生的断裂带，众多学者从多个角度对其强度进行了计算，同时也拓展了断裂带的内涵。为提高断裂带强度计算的有效性，对未来断裂带计算方法本文提出如下几点建议：

（1）降低特征变量的相关性对断裂带强度的影响。用来计算断裂带强度的特征变量可能存在一定的相关性，如果不考虑该因素的影响，会过分放大或忽视团队内部的断裂带。

（2）考虑断裂带的动态变化。由于人类情感因素对其归属感的影响，团队内断裂带也处于不断变化中，因此基于团队成员固定人口统计学特征的计算方法存在一定局限性。即使在计算断裂带过程中考虑人的情感因素，也只是得到团队在某一时间截面的断裂带情况，难以体现子团体之间成员的变动情况。

（3）引入断裂带激活因子。相同的断裂带在激活和休眠状态下其对团体绩效的影响是不同的，因此不同状态下的断裂带强度也应有所差别。引入断裂带激活因子可以使计算得到的断裂带强度更加符合实际，但是确定有效的断裂带激活因子还有待进一步探索。

［1］Lau D C，Murnighan J K.Demographic Diversity and Faultlines：The Compositional Dynamics of Organizational Groups［J］.Academy of ManagementReview，1998，23（2）：325-340.

［2］Thatcher SM，Jehn K A，Zanutto E.Cracks in Diversity Research：The Effects of Diversity Faultlines on Conflict and Performance［J］.Group Decision and Negotiation，2003，12（3）：217-241.

［3］Gibson C，Vermeulen F.A Healthy Divide：Subgroups as a Stimulus for Team Learning Behavior［J］.Administrative ScienceQuarterly，2003，48（2）：202-239.

［4］Shaw JB.TheDevelopmentand AnalysisofaMeasureofGroup Faultlines［J］.OrganizationalResearchMethods，2004，7（1）：66-100.

［5］Li J，Hambrick D C.Factional Groups：A New Vantage on Demographic Faultlines，Conflict，and Disintegration in Work Teams［J］.Academy of Management Journal，2005，48（5）：794-813.

［6］Bezrukova K，Jehn K A，Zanutto E L，et al.Do Workgroup Faultlines Help or Hurt？A Moderated Model of Faultlines，Team Identification， and Group Performance［J］.Organization Science，2009，20（1）：35-50.

［7］Van Knippenberg D，Dawson JF，WestM A，etal.Diversity Faultlines，Shared Objectives，and Top Management Team Performance［J］.Human Relations，2011，64（3）：307-336.

［8］Lawrence B S，Zyphur M J.Identifying Organizational Faultlines with Latent Class Cluster Analysis［J］.Organizational Research Methods，2011，14（1）：32-57.

10.3969/j.issn.1673-0194.2015.01.058

F270

A

1673-0194（2015）01-0115-03

2014-07-06

肖明（1963-），男（蒙古族），内蒙古通辽人，北京科技大学东凌经济管理学院教授，博士生导师，主要研究方向：公司投融资决策。