软弱地层锚索预应力蠕变损失研究

吴明雷,李禄(济南市勘察测绘研究院,山东济南 250013)

软弱地层锚索预应力蠕变损失研究

吴明雷∗,李禄
(济南市勘察测绘研究院,山东济南 250013)

摘 要:多个工程实例表明:岩土体蠕变易引起锚固工程支护结构加固频繁、锚索重新张拉等工程病害,严重者导致锚固力失效,锚固工程失稳,如若处理不当,将直接危及施工人员的生命财产安全；本文以济南市某深基坑工程案例为依托,将岩土体由经典的广义Kelvin体代替,推导了其本构方程、蠕变方程、松弛方程,从理论上分析了锚索蠕变变形对预应力损失的贡献大小；并结合现场测试数据对比可知:该模型能够较好的反映蠕变变形引起的损失趋势,由数据软件拟合公式可知,理论计算结果与测试数据偏差不大,论证了上述分析的可靠性,为今后锚固工程的设计、施工提供了理论依据和技术支持。

关键词:软弱地层；蠕变变形；预应力损失；本构方程

1　引 言

近年来,虽然预应力锚固工程作为一种新的结构形式已被广泛的应用于边坡和深基坑工程的支护结构中,但由于蠕变损失引起锚固力失效,导致工程失稳现象却屡见不鲜[1～3];这是由于锚固机理的模糊性和影响因素的多样性,使得蠕变引起的锚固力损失具有一定的区域性,在短时间内难以形成理论上通解;研究发现:现有锚固工程中,岩土体蠕变引起的预应力损失多为半经验半理论解,因此,开展区域性研究,针对特定工程进行蠕变损失进行分析具有重要的经济价值和工程意义。

目前,岩土体蠕变引起的预应力损失的理论研究成果很多;比如:孙钧、韩光、王渭明、丁多文[4～7]等通过对锚索预应力损失影响因素进行分类,将锚索自由段和锚固段分开考虑,对锚固段蠕变损失进行了定量分析,并给出了相应的计算公式;张发明、景峰、王清标[8～10]等依据不同的蠕变模型对锚索预应力损失进行了理论计算,并结合实际工程进行了工程应用;张金龙、陈安敏、龚寒梅[11～13]等基于蠕变试验,对不同的加载方式、张拉荷载及张拉次数下蠕变预应力损失进行了理论计算分析,并结合室内试验测试结果进行了探讨。

研究认为:蠕变变形对锚索预应力损失贡献率较大,约占预应力总损失的15%～25%[4～6],是预应力损失的重要组成部分;本文在参考相关文献的基础之上,以济南市某深基坑工程为工程依托,将岩土体以经典的广义Kelvin体代替,从理论上对岩土体蠕变变形引起的锚索预应力损失进行了计算分析;并结合现场为期60天的锚固力测试结果对比发现:该蠕变计算模型能够较好的反映锚索预应力损失变化趋势,3道锚索蠕变损失率分别16%、19%、18%;经数据拟合可知:理论计算值与现场测试数据误差相差不大,论证了上述分析的可靠性,从而为今后同类工程的设计、施工提供了有利的理论依据和技术支持。

2　岩土体蠕变损失机理分析

岩土体是一种力学性质非常复杂的介质,在不同工况下表现出不同的粘弹塑性特征;其自身的不连续性和各向异性使得受荷区内部结构和单元在外荷载下产生塑性压缩和相对变位,这是蠕变变形的根本原因[3];当其受力状态改变时,所表现出来的弹粘塑性属性也不同;工程实例表明:任何工况下的岩土体介质属性均属于弹粘塑性的组合;当岩土体越密实完整,其蠕变性质就越差;反之,岩土体越破碎松散,则压缩产生变形越大,蠕变越显著。

预应力工程锚固技术是指通过注浆技术,将锚固段与周围岩土体整合成一个整体,形成共同的工作体系,一起承担开挖面滑移产生的拉力;假定锚固体与围岩不发生相对滑移错动,则当岩土体发生蠕变变形△L,从AB→A′B′时,其锚索也随之发生相对应的位移,进而引起锚索相应的预应力损失;反之,当锚固力变化时,也会造成锚固体蠕变变形产生相对位移。如图1所示:

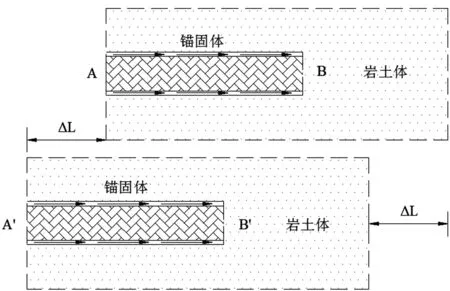
图1　锚固体蠕变损失示意图

3　蠕变效应的损失计算

3．1蠕变模型的提出

岩土体不同的介质属性是弹粘塑性的不同组合,而由文献[6]可知:不同的蠕变模型可描述不同的蠕变阶段,代表着不同的属性组合;因此,当岩土体蠕变计算模型表现出不同的属性组合时,其计算模型也应是常见流变模型组合而成的复合流变模型。

岩土体蠕变计算模型是通过不同的弹性、黏性元件的串并联组合来共同描述其蠕变不同阶段;已知Maxwell体和Kelvin体仅可描述岩土体蠕变三阶段中某一阶段,而不能描述其完整的蠕变过程;而广义开尔文体综合了上述两模型的共同特点,可以描述蠕变的第一第二阶段,弥补了上述两计算模型的不足,是现有理论中比较理想的反映岩土体蠕变的复合简化模型如图2所示。

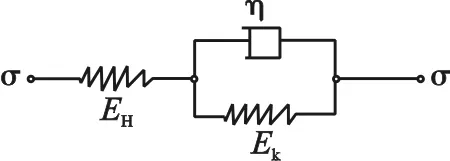
图2　蠕变损失计算模型

3．2特征方程的推导

该模型是由一个Kelvin体和一个胡克体串联而成的三元件模型,弥补了Kelvin体的不足,既可以描述瞬时弹性变形,同时具有松弛特性。

(1)本构方程

已知Kelvin体本构方程:

σk=Ekεk+ηk.εk (1)

由静力平衡条件得:

则推导其本构方程为:

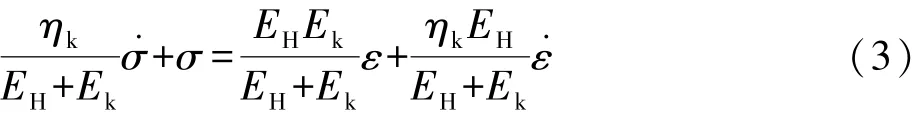
(2)蠕变方程

当σ=σc=A,t＞0时,.σ=0,式(3)可化为:

一元一次微分方程初始条件:t=0,ε=σc

EH

;

而当考虑在时间t=t1时全部卸载,则弹性体变形在卸载瞬间恢复,式(3)可化为:

ηk.ε+Ekε=0(6)

初始条件:当t=t1时,

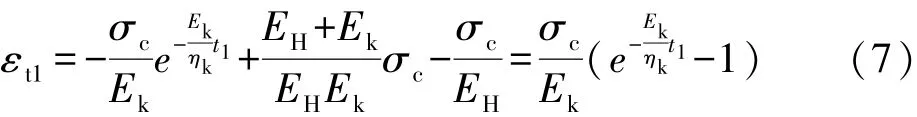
则蠕变方程可由下式表示:

已知当t=∞时,式(8)中ε→0,可见其只可描述弹性后效,无黏性流动现象。

(3)松弛方程

当ε=εc=C时,式(3)可化为:

则卸载后蠕变方程的解为:

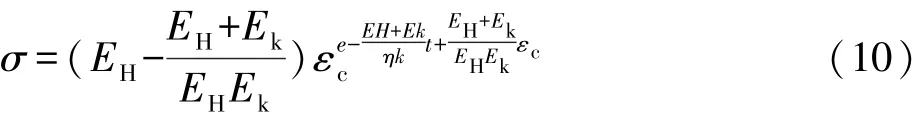
由式(10)可知:σ随着时间t的增加而减少,因此其只可描述松弛特性。图中Eh、Ek、ηk则表示为岩土体等效的弹性、黏性参数。

已知当t=0时,σ=EHεc,则松弛方程为:

4　算例

4．1工程概况

济南市某深基坑工程位于西客站附近,地层上部以黄河、小清河冲积而成的黏性土、粉土为主,下部主要为山前冲洪积而成的黏性土、砂土、卵石土;相应土层及物理力学参数如表1所示。

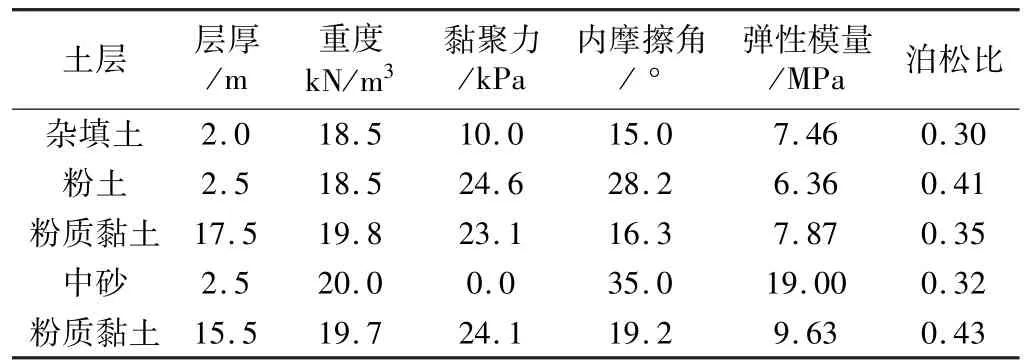
土层物理力学参数 表1

基底相对标高为-19．500 m,基坑上部采用1∶3放坡开挖,三道土钉墙支护:下部采用桩锚支护结构:其中桩结构采用长23 m,Φ800 mm@3 m的钻孔灌注桩;桩顶-7．5 m处设置800 mm×1 000 mm的冠梁,下部基坑在-12．0 m、-16．0 m处设置2[28a型槽钢做腰梁,三道锚索均采用4根7Φ15．24高强度低松弛钢绞线,自上而下分别设置在冠梁和两道腰梁上,其长度分别为25 m、30 m、25 m;其中锚固段长16 m、21 m、20 m;自由段长度分别为9 m、7 m、5 m;设计预应力值依次是自150 kN、200 kN、180 kN,灌浆材料采用C20水泥砂浆;垫板采用20 mm×240 mm ×240 mm的钢板,锁具采用M15-9圆塔形多孔翻锚及配套夹片;后张法施工,采用两台张拉机具从槽钢两端向中间同时张拉,减弱了群锚效应产生的预应力损失,如图3所示。

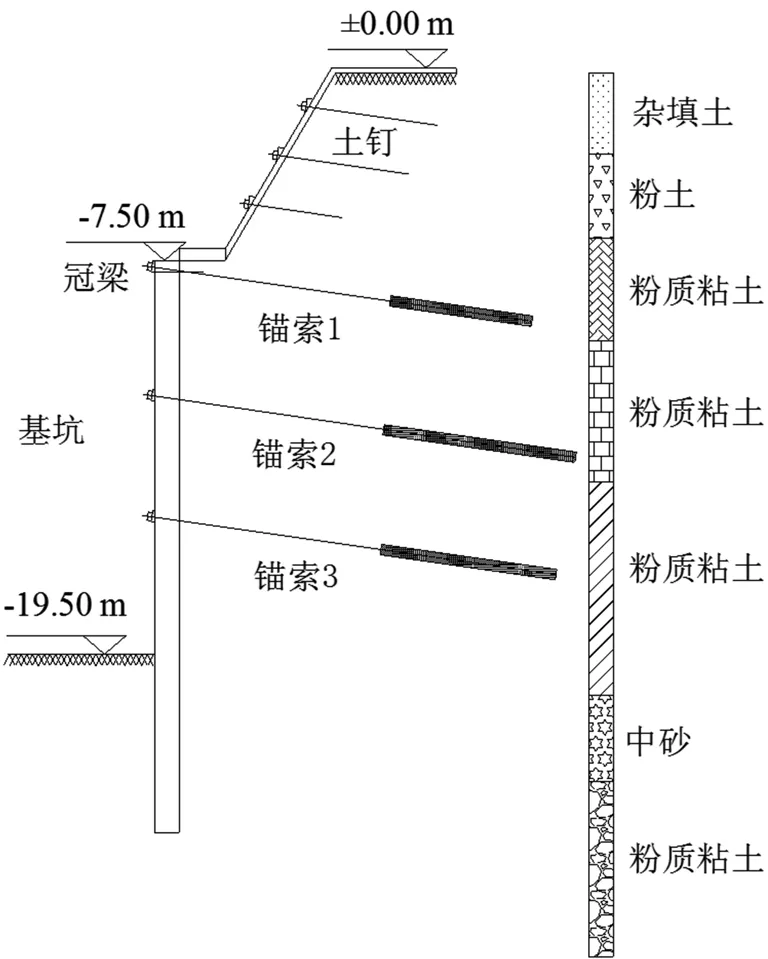
图3　基坑支护结构图

4．2预应力锚索测力计的布置及安装

轴力检测计则采用灵敏度高、稳定性好的MSJ-201钢弦式锚索应力计;传感器的测试原理是利用张紧的钢弦在不同张力情况下其自振频率不同,通过数模转换器测试其钢弦的频率,通过反算得到实际的压力值。如图4所示:

4．3理论计算

锚固段周围锚索张拉力作用下发生蠕变变形,则上述蠕变公式可改写成下式表示:

当采用超张拉时,则近似考虑在蠕变变形完成时(t→∞),岩土体蠕变变形可用下式表示:

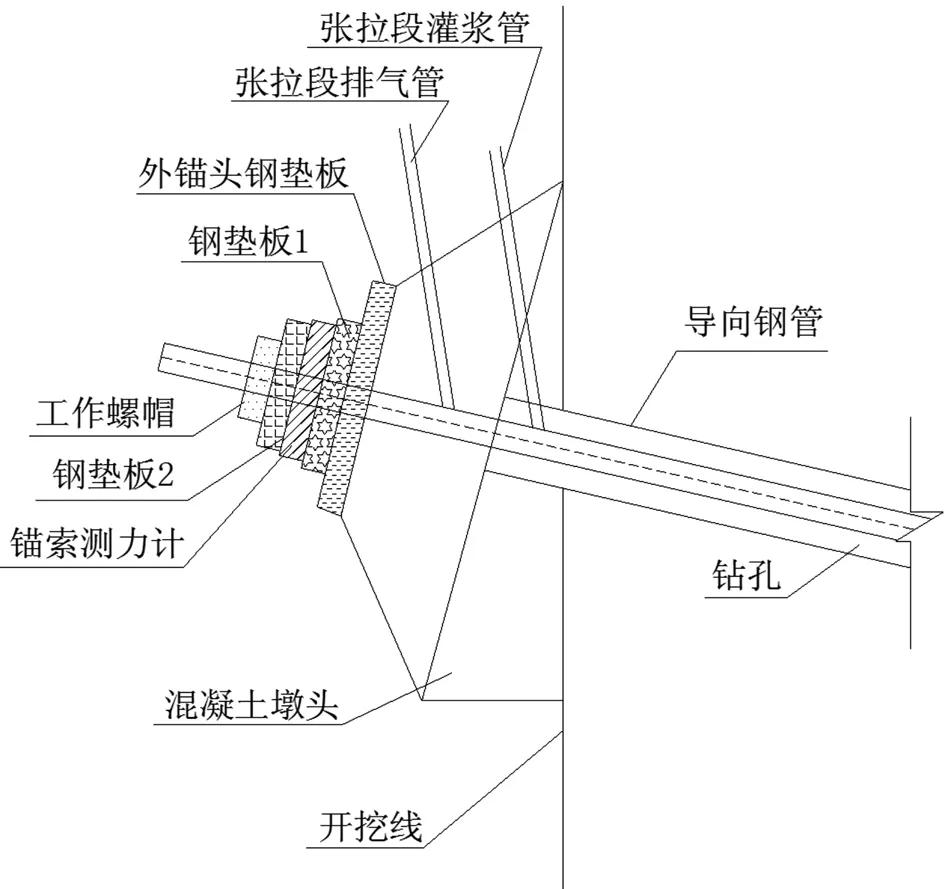
图4　锚索轴力计安装示意图

式中:Ek为锚索锚固段的回弹模量,EH为锚索自由段的回弹模量,取200 GPa;明显可知:蠕变变形可以看成是锚索自由段和锚固段的变形叠加;假定锚固体蠕变变形满足小变形假设,σc为锁定后锚索预应力初值,则在正应力作用下锚固体瞬时弹性变形可由下式表示:

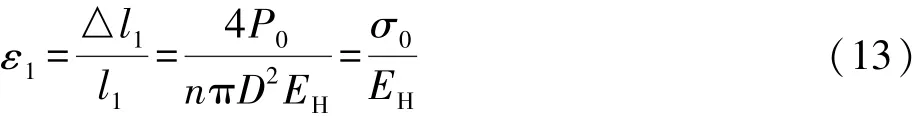
明显可知:求解蠕变变形引起的应变值,只需求解锚固体弹性参数即可;已知蠕变试验参数是指土体在逐级加载下达到破坏的极限系数,而实际中锚固体周围土体未达到极限状态,因此蠕变试验参数不能直接应用于实际工程。文献[6]中依据土体蠕变最终变形与压缩变形相同,同时结合Kelvin体延迟时间td的表达式,求得锚固体弹性模量Ek及低应力状态黏性模量η,取得了良好的工程实践效果。

式中E为土的弹性模量,Es为压缩模量。取富水黏性土td=100 h,则求得η=9．72×1012Pa·S,与蠕变试验测得数值η=1．14×1013Pa·S相近。

由式(11)～式(14)可知:3道锚索蠕变变形量△l=△l1+△l2=11．383 mm、16．875 mm、12．723 mm;则相应预应力损失为△P =51 kN、63 kN、57 kN。可以看出,蠕变变形引起的预应力损失较大,约占预应力总损失的30%,是预应力损失的重要组成部分。

5　现场测试结果对比

为掌握岩土体蠕变变形对锚索预应力损失的贡献率,进行了专项锚索轴力监测方案,通过对张拉后试验锚索为期60天的锚固力测试,以期准确掌握3道锚索预应力损失变化规律,如图5所示;研究发现:经典的广义Kelvin体蠕变计算模型可较好的反映锚索预应力损失的变化趋势;依据工程经验结合理论分析,当3道锚索进行超张拉率分别为33%、30%、31%时,锚索长期预应力可维持在设计值150 kN、200 kN、180 kN,保证了锚固效果的安全可靠;当锚索张拉后60天后,锚固力基本保持在设计值附近不变,这说明:低拉应力作用下,蠕变变形在第20天时已完成80%,在历时60天时,蠕变变形已基本完成,后期引起的蠕变损失可忽略。

图5　锚索预应力损失特征

由数据处理软件origin进行公式拟合可知:锚索实测轴力值均可用下式表示:x

与式(11)锚索蠕变变形计算公式形式相符,其中对三道锚索数据汇总于表2如下:

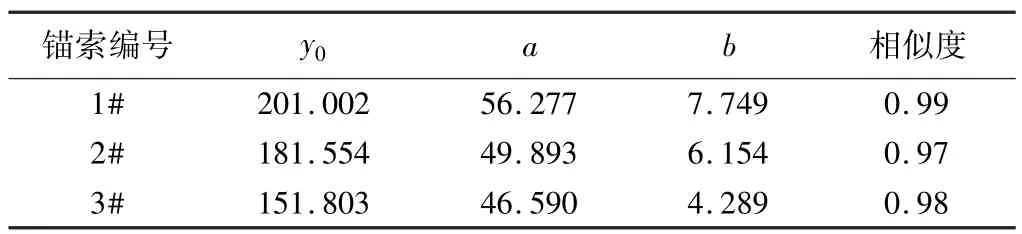
数据拟合参数汇总 表2

研究发现:上述为瞬时损失和蠕变损失的总和,为研究岩土体蠕变变形对锚索预应力损失的影响,我们专门针对三道锚索张拉后2 h内进行了轴力测试试验如图6所示,可知:3道锚索的短期损失量分别为14 kN、22 kN、18 kN;为预应力设计值的9%～11%;因此,岩土体蠕变变形引起的锚索预应力损失率为19%～24%,与相关文献[14～16]中相符。

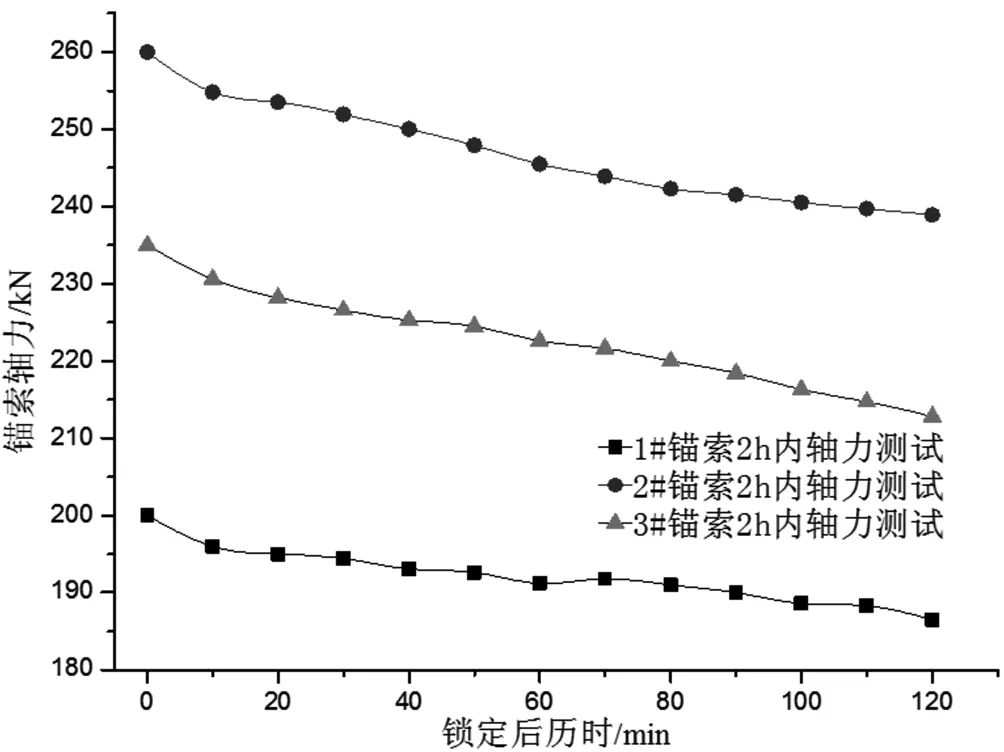
图6　张拉锁定2h内轴力-时间曲线

6　结 语

(1)根据济南地质特点,以经典的广义Kelvin体计算模型描述了岩土体蠕变特征,并推导了其相应的本构方程、蠕变方程、松弛方程;从理论上分析了岩土体蠕变变形对预应力损失的贡献大小。

(2)通过对3道试验锚索进行了为期60天的现场测试结果发现:测试结果与理论计算结果相近,其相应1#、2#、3#锚索蠕变损失率分别为21%、23%、21%和24%、19%、21%;论证了上述分析的可靠性。

(3)通过origin对现场测试数据进行拟合分析,总结了锚索长期蠕变损失的经验预测公式可由:

y=y0+ae-x

b 表示;其中:y0、a、b均为参数;为今后同类工程的施工、设计提供了一定的理论依据和技术支持。

参考文献

[1] 江权,陈建林,冯夏庭等．大型地下洞室对穿预应力锚索失效形式与耦合模型[J]．岩土力学,2013,34(8):2271 ～2278．

[2] 徐明,张琴,唐树名等．锚索失效对边坡稳定性影响的数值研究[J]．地下空间与工程学报,2008,4(5):865～869．

[3] 李英勇,张顶立,张宏博等．边坡加固中预应力锚索失效机制与失效效应研究[J]．岩土力学,2010,32(1):144～150．

[4] 孙钧．岩石流变力学及其工程应用研究的若干进展[J]．岩石力学与工程学报,2007,26(6):1081～1106．

[5] 韩光,朱训国,王大国．锚索预应力损失的影响因素分析及其补偿措施[J]．辽宁工程技术大学,2008,27(2):176～179．

[6] 王渭明,曹正龙,王刚刚等．厚冲击层锚索预应力损失研究[J]．岩土工程学报,2014,36(9),1607～1673．

[7] 丁多文,白世伟,罗国煜．预应力锚索加固岩体的应力损失分析[J]．工程地质学报,1995,3(1):65～69．

[8] 张发明,赵维炳,刘宁等．预应力锚索锚固荷载的变化规律及预测模型[J]．岩石力学与工程学报,2004,23(1): 39～43．

[9] 景峰,余美万,边智华等．预应力锚索预应力损失特征及模型研究[J]．长江科学院院报,2007,24(5):52～55．

[10] 王清标,张聪,王辉等．预应力锚索锚固力损失与岩土体蠕变耦合效应研究[J]．岩土力学,2014,35(8):2150 ～2162．

[11] 张金龙,徐卫亚,徐飞等．深卸荷变形拉裂岩体锚索预应力损失规律研究[J]．岩石力学与工程学报,2009,28 (2):3965～3970．

[12] 陈安敏,顾金才,沈俊．软岩加固中锚索张拉吨位随时间变化规律的模型试验研究[J]．岩石力学与工程学报, 2002,21(2):251～256．

[13] 龚寒梅．群锚预应力损失分析[D]．昆明:昆明理工大学,2013．

[14] 李英勇,王梦恕,张顶立．锚索预应力变化影响因素及模型研究[J]．岩石力学与工程学报,2008,27(S1):3140 ～3146．

[15] 周永江,何思明,杨雪莲．预应力锚索的预应力损失机理研究[J]．岩土力学,2006,27(8):1353～1356．

[16] 唐孟雄．基坑工程预应力锚索锚固力实验研究[J]．岩石力学与工程学报,2007,26(6):1158～1163．

[17] 叶海林,郑颖人,李安洪等．地震作用下边坡预应力锚索振动台试验研究[J]．岩石力学与工程学报,2012,31 (S1):2847～2854．

[18] 丁秀丽,盛谦,韩军．预应力锚索锚固机理的数值模拟实验研究[J]．岩石力学与工程学报,2002,21(7):980～988．

[19] 张发明,陈祖煜,刘宁．岩体与锚固体间粘结强度的确定[J]．岩土力学,2001,22(4):470～473．

[20] 叶惠飞．锚索预应力损失变化规律分析[D]．杭州:浙江大学,2004．

Creep Loss Research of Anchor Prestressing in Soft Ground

Wu Minglei,Li Lu
(Jinan Geotechnical Investigation and Surveying Research Institute,Jinan 250013,China)

Abstract:Through collating and analyzing the existing data of engineering examples,rock creep can lead the anchorage support re-tensioned and repaired frequently,which could further result in the failure of the anchoring force and the instability of the anchor project;If it should not be handled properly,the life and property safety of construction workers were endangered;One deep pit of Jinan City was taken as an example,the creep calculation model was replaced as general Kelvin,the corresponding constitutive equations,creep equation,relaxation equation were deduced;The theoretical calculation of the anchor prestressing loss which result of creep deformation was analyzed;Comparison of theoretical calculation result and field test data shows that:the creep calculation model can better reflect the cable prestressing loss trends; the fitting formula demonstrated the reliability of the above analysis;it provided a theoretical basic and technical support for the design and construction of similar anchor project in the future．

Key words:soft ground;creep deformation;prestressing loss;constitutive equations

文章编号:1672-8262(2015)05-167-05中图分类号:TU472．3

文献标识码:A

收稿日期:∗2015—06—20

作者简介:吴明雷(1986—),男,助理工程师,主要从事岩土工程的勘察、设计工作。