基于参数增量的地质储量增量近似劈分方法

孙立春 蒋百召 何 娟 倪军娥 汪洪强 郭丽娜 王 龙

（中海油研究总院 北京 100028）

基于参数增量的地质储量增量近似劈分方法

孙立春 蒋百召 何 娟 倪军娥 汪洪强 郭丽娜 王 龙

（中海油研究总院 北京 100028）

孙立春，蒋百召，何娟，等.基于参数增量的地质储量增量近似劈分方法［J］.中国海上油气，2015，27（2）：48－52.

Sun Lichun，Jiang Baizhao，He Juan，et al.An approximate method to breakdown the OOIP based on the OOIP－estimate parameter increments［J］.China Offshore Oil and Gas，2015，27（2）：48－52.

剖析了目前业内广泛应用的地质储量变化增量劈分方法的不足，即简单地将各储量参数变量引起的储量增量平均化，不能客观反映各储量参数的变化对储量变化值的影响。在储量参数与储量无量纲化基础之上，提出了考虑各储量参数增量对储量增量的差异化影响的观点，推导出了新的地质储量增量近似劈分公式，分析对比了不同劈分方法的应用效果，并简要探讨了储量参数敏感性分析及储量不确定性分析的思路。本文提出的方法可以应用于其他类似的基于参数增量的增量劈分，具有较广泛的实际应用价值。

地质储量；储量参数；增量；近似劈分

1 问题的提出

地质油藏研究在任何阶段都会存在不确定性，因而导致了每个特定阶段的储量研究结果与此前的认识都会有差异［1－2］。以往针对储量变化的研究，一方面集中于储量参数敏感性、储量结果的不确定性及储量变化原因等［3－6］；另一方面集中于尝试解决储量各参数变化对储量差异的定量贡献，以期知道某些参数变化引起的地质储量变化量［1，7］。然而，不同评估点评估时，对于同一储量单元，多个储量计算参数可能同时发生变化，因此储量差异是多个参数共同作用的结果。对于储量评价而言，如何评价各个参数的变化引起的储量变化大小以及确定哪些参数是储量变化的最敏感参数是必要的，因此基于储量计算参数的地质储量增量劈分方法的选择及劈分结果分析十分重要［7－10］。

就2个不同储量评估点而言，分析导致储量评估差异（增量）的因素及各因素对储量增量贡献率的大小十分重要，但目前很少有此方面的研究。以往基于单因素分析的储量变化存在2个方面的不足，一方面是各个单因素引起的储量增量与全油气田的储量增量变化并不一定闭合，另一方面是因为储量变化是多个因素共同作用的结果，所以基于单因素分析不足以反映真实的储量变化原因。针对这一问题，范尚炯 等［7］以石油地质储量计算公式为例，提出了考虑多个参数共同作用引起储量变化的思路，并进行了贡献量的定量劈分研究。目前文献［7］方法已被国内储量工作者广泛借鉴引用，其研究思路如下。

设复算前的储量为

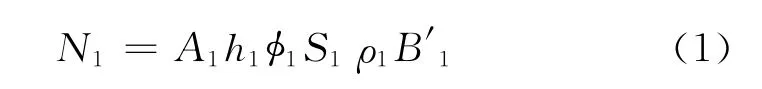
复算后的储量为

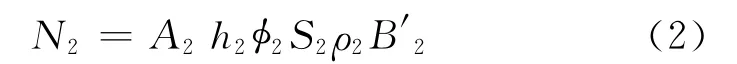
式（1）、（2）中：N为地质储量；A为含油面积；h为有效厚度；为有效孔隙度；S为原始含油饱和度；ρ为地面原油密度；B′为地层原油体积系数的倒数；下标1、2分别代表复算前后。

若2次储量计算的参数增量和储量增量都用Δ表示，则

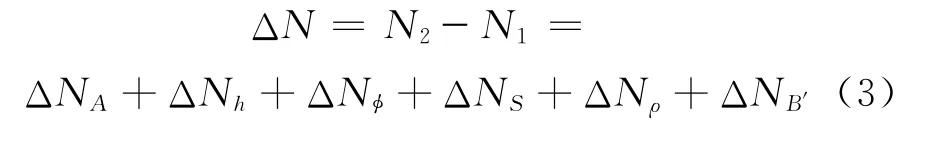
即

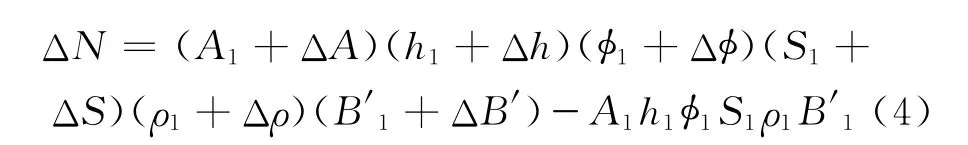
式（4）展开后，将每项依次分配给6个储量参数对应的储量增量，其分配方法如下：仅带有1个参数增量的项就将对应的储量增量分配给这一个参数；带有2个、3个、…、6个参数增量的，分别以1/2、1/3、…、1/6将储量增量分配给相应的参数增量；之后，分别累加各参数增量所对应的储量增量，即可得到各参数变量所引起的储量增量。

笔者认为，上述方法的主要思路是可以借鉴的，即将前后两次的储量增量分别劈分到各个相关储量参数增量所引起的变化量，从而分析出每个参数增量对油气田储量增量（变化量）的贡献值。但上述方法的缺陷在于得到各个展开项后，带有Δ参数项（即参数增量）的分配采用了等权的分配，并没有考虑各个储量参数增量之间相对大小的关系。因此，笔者针对这一问题进行了研究，在储量参数和储量无量纲化的基础上，提出了考虑各储量参数变化对储量增量差异化影响的观点，推导出了新的地质储量增量近似劈分公式，分析对比了不同劈分方法的应用效果，并简要探讨了储量参数敏感性分析及储量不确定性分析的思路。

2 基于参数增量的地质储量增量近似劈分方法

2.1 公式推导

如果将式（4）展开，共26－1＝63项，可以写成

笔者认为应考虑以下2个方面的修正：

1）根据不同储量参数增量之间的相对大小进行分配；

2）由于每个储量参数增量都是有量纲的，如果直接根据参数增量数值的绝对大小进行分配，则所对应的储量增量之间的相对大小受到所用量纲的影响，因此不能直接采用式（5）进行分配，须先进行无因次化。

设

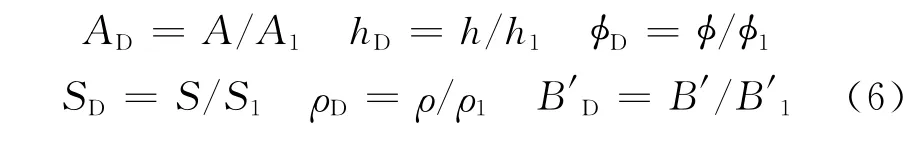
则复算前后储量，即式（1）、（2）经无因次化后分别变为

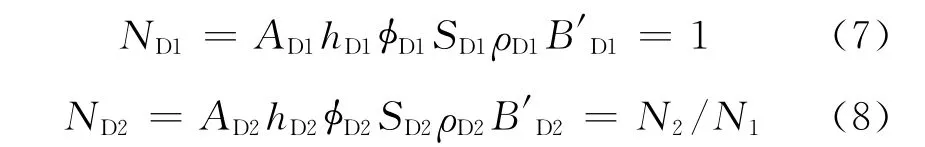
此时无因次的储量增量ΔND可表示为参数增量（无因次）所引起的储量增量（无因次）：

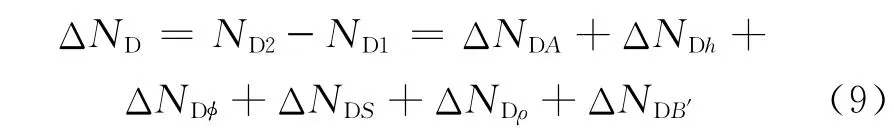
即

将式（10）展开，可以写成

也就是说，ΔND实际上是由这63项组成的。通过与式（9）对比，可认为这63项对应于ΔNDA、ΔNDh、ΔND、ΔNDS、ΔNDρ及ΔNDB′储量增量（无因次）。

由于式（11）中与每个参数增量有关的项都是32项，因此研为原始含油饱和度将32项中包含有ΔAD、ΔhD、ΔD、ΔSD、ΔρD、ΔB′D中一个或多个储量参数增量的项进行合理劈分，从而分别得到对应于每个储量参数增量（无因次）的储量增量（无因次）。

以ΔNDA为例，它表示的储量增量仅是ΔAD引起的，因此凡是式（11）中包括ΔAD的项都须进行合理劈分，以得到仅是ΔAD引起的无因次储量增量，即

式（12）中：ΔNDA－i为式（11）中包括ΔAD的某一项。为了便于理解，分别以式（11）中与储量增量ΔNDA有关的包括1个、2个及6个储量参数增量的部分项为例，分析如何进行劈分（其他项的劈分原则与之相同）。

1）式（11）中第一项只包括ΔAD这一个参数增量，因此认为该项引起的储量增量（无因次）都是ΔAD的贡献量。

2）式（11）中ΔADΔhD项只包含2个参数增量ΔAD、ΔhD，因此认为该项的计算值应是2个参数变量共同作用的效果。

设

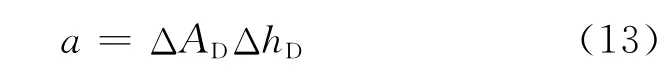
若2个变量所做的贡献分别为a1、a2，显然

对于a而言，无论结果是正还是负，在式（13）右边的连乘因子中只有2个变量对结果的贡献与绝对值的相对大小有关，可将其作为“权重”来理解，则

由式（13）～（15）可得参数在此项中储量无因次增量的贡献量

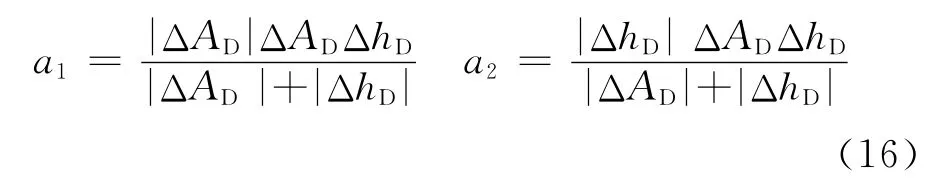
3）式（11）中最后一项ΔADΔhDΔDΔSDΔρDΔB′D包含6个参数增量。同理，对于其中某一参数而言（仍以ΔAD为例），容易得到它在此项中的储量无因次增量的贡献量为

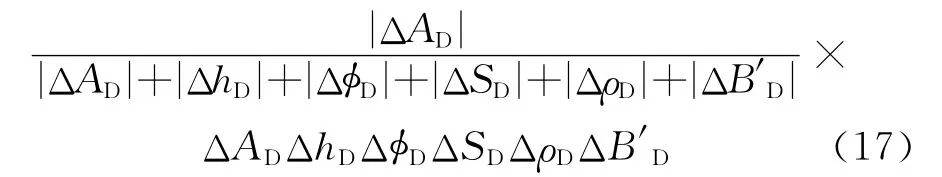
而实际的储量增量贡献量应为各增量（无因次）再乘以N1，即

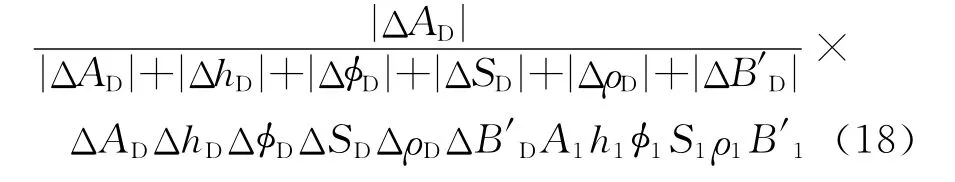
2.2 结果比较

根据修正后的公式，对文献［7］中的案例进行重新计算，并与之前的计算结果进行了比较（表1）。

表1 某区块储量复算前后参数变化及储量劈分比较Table 1 Parameters change and comparison of original oil in place before and after recalculating original oil in place of a block

从表1可以看出，2种方法计算结果有一定的差异，但不明显，分析认为主要是由于该案例的特殊性导致了2种方法的近似，使得文献［7］方法的不合理性没有完全反映出来。为更好地反映本文方法的特点及文献［7］方法的不足，将某一个储量参数的变化量（本文中选取含油面积）进行差异化处理，特将表1中的复算前后的含油面积设计了2种替换方案，并分别采用文献［7］方法及本文方法进行试算，结果分别见表2、3。

表2 储量参数变换后的储量劈分结果（方案1）Table 2 Results of original oil in place after parameter change（case 1）

表3 储量参数变换后的储量劈分结果（方案2）Table 3 Results of original oil in place after parameter change（case 2）

表2中复算前后含油面积分别为5、15 km2，而表3中复算前后含油面积分别为5、50 km2，其他参数在两方案中保持相同。从表2、3可知，2种方法劈分结果差异较大：表2中含油面积增量与有效厚度增量倍数分别为2.00及0.82，文献［7］方法所估算的含油面积与有效厚度这2个参数对应的储量增量之比为2.05，本文方法所估算的储量增量之比为3.70；而表3中仅含油面积发生了明显变化，含油面积增量与有效厚度增量倍数变为9.00及0.82，2种方法对应的含油面积增量与有效厚度增量的储量增量之比分别为2.78、11.10。

值得注意的是，在方案2中复算后含油面积由原来的3倍增大到原来的10倍，而其他参数增量倍数保持与方案1一致的情况下，使用文献［7］方法所得含油面积增量与有效厚度增量所对应的储量增量之比仍不到3（试算结果表明，即使含油面积增加到原来的100倍，储量增量之比仍为3左右），显然不太合理。这主要是因为文献［7］方法在储量劈分时仅考虑了参数变化的个数，对于参数增量之间的相互大小并没有考虑；而本文方法既考虑了参数变化的个数，也考虑了各个参数变化量的相对大小。由此可见，本文方法既解决了各储量参数增量所对应的储量增量劈分的闭合问题，也解决了各储量参数增量之间相对大小的一致性，即采用无因次化的处理方式实现了各储量参数之间可比较性。相对而言，本文方法更为客观。

3 几点讨论

1）参数变量的敏感性，即确定储量参数对地质储量的相对影响大小，除了采用上述方法来确定之外，还可以直接比较参数增量之间的大小，即在不须弄清储量参数对储量增量的实际贡献，只是了解储量参数变化对储量变化结果的敏感性时，可以采用储量参数增量的倍数变化来进行推导。

复算前的储量计算可用式（1），复算后的储量为

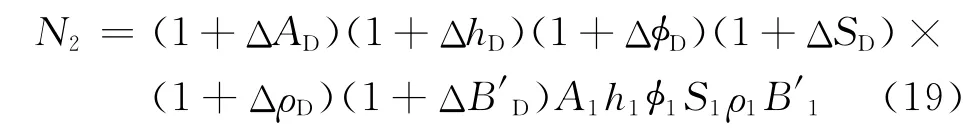
直接比较ΔAD、ΔhD、ΔD、ΔSD、ΔρD、ΔB′D这几个参数的大小（即参数增加倍数），就可以判断哪个参数的变化相对影响较大。但须注意，这只是确定储量参数对地质储量影响的相对大小，而不能利用其进行储量增量的劈分。

2）本文提出的储量增量近似劈分是基于参数变量增量引起的储量增量，针对式（11）中展开的某一项中，各参数增量（无量纲化后）引起的储量增量（无因次）与参数增量（无因次）之间的比例关系是一致的。也就是说，对于式（11）某一展开项而言，如果含油面积增加了1倍，而有效厚度变为之前的0.5倍，则认为这2个变量引起的储量增量应是4∶1的关系。但值得注意的是，对于所有项而言，实际的储量增量并不一定是这个关系。

3）尽管本文提出了这种近似的储量增量劈分方法，但实际上对于一个同时受多个因素共同控制的实体而言，由于因素之间的互相依赖、相互作用，决定了它们共同作用效果劈分的不易性。从严格意义上来讲，只有时间上有先后、成因上有主次的才能进行劈分，这也是多因素分析所要求的，如果进行作用效果的劈分，这是一种单因素的分析。因此，笔者认为，任何一种对受多因素影响的对象进行单因素的劈分都是一种近似，但近似的方法也需要在理论上可行、实践上可操作。

4）不能采用本文方法开展基于参数变化范围的敏感性和地质储量的不确定性研究，建议采用基于概率法模拟的不确定性研究方法，以便更好地得到敏感性参数及不确定性的分布范围［11－15］。

4 结论

1）本文推导的储量增量近似劈分方法体现了每个储量参数的差异及其对地质储量增量的不同贡献。除了实现储量增量的闭合之外，在进行储量变化量的劈分时既考虑了参数增量的个数，也考虑了参数自身在变化前后的相对大小，同时还考虑了各个参数增量之间的相对大小。

2）对于一个同时受多个因素共同控制的实体而言，基于参数变量对结果的劈分都是一种近似结果，但劈分方法应尽量体现变量之间的相关关系及其地质意义。

3）本文提出了储量参数敏感性研究的不同处理方式。在只须确定性了解储量参数对储量增量的相对大小时，可以采用参数“倍数”变化的方式直接得知；但在每个储量参数存在一定变化范围时，建议采用概率法模拟的方式研究它们对储量增量的敏感性及其地质储量的不确定性。

［1］胡允栋，关涛.储量参数误差对储量精度的影响［J］.石油勘探与开发，1998，25（6）：70－73.

Hu Yundong，Guan Tao.The influence of errors in volumetric parameters on OIP/GIP estimation［J］.Petroleum Exploration and Development，1998，25（6）：70－73.

［2］毕海滨，查全衡，王永卓.提高储量评估水平的三大地质要素［J］.石油学报，2004，25（1）：25－29.

Bi Haibin，Zha Quanheng，Wang Yongzhuo.Three geological factors for improving estimation quality of original oil in place［J］.Acta Petrolei Sinaca，2004，25（1）：25－29.

［3］王亚青，高博禹，孙立春.提高地质储量计算精度需注意的几个问题［J］.西南石油大学学报：自然科学版，2011，33（5）：63－67.

Wang Yaqing，Gao Boyu，Sun Lichun.Some problems in improving caculation precision OOIP［J］.Journal of Southwest Petroleum University：Science ＆Technology Edition，2011，33（5）：63－67.

［4］鲁国明.油藏评价阶段造成探明储量计算偏差的主要因素分析［J］.油气地质与采收率，2010，17（6）：30－34.

Lu Guoming.Analysis on calculation errors of reserve estimation during the reservoir evaluation stage［J］.Petroleum Geology and Recovery Efficiency，2010，17（6）：30－34.

［5］张文昭.提高油气储量精度的关键［J］.勘探家，1998，3（1）：9－10.

Zhang Wenzhao.Improving accuracy of hydrocarbon reserve estimation［J］.Petroleum Explorationist，1998，3（1）：9－10.

［6］王允洪，邬庆良，马建德.东海P油气田储层储集参数估算再认识［J］.海洋石油，2000，（1）：15－21.

Wang Yunhong，Wu Qingliang，Ma Jiande.Re－recognition of reservoir parameters estimation in P oil field，the East China Sea［J］.Offshore Oil，2000，（1）：15－21.

［7］杨通佑，范尚炯，陈元千，等.石油及天然气储量计算方法［M］.2版.北京：石油工业出版社，1998：114－116.

Yang Tongyou，Fan Shangjiong，Chen Yuanqian，et al.Methods of oil and gas geologic reserves calculation［M］.2nd ed.Beijing：Petroleum Industry Perss，1998：114－116.

［8］陈军，张烈辉，冯国庆，等.低渗透气藏III类储层对产能的贡献研究［J］.天然气工业，2004，24（10）：108－110.

Chen Jun，Zhang Liehui，Feng Guoqing，et al.Contribution of third class reservoirs to productivity of low permeable gas pools［J］.Natural Gas Industry，2004，24（10）：108－110.

［9］吕靖，宋保全，刘吉余.高含水期地质储量劈分方法［J］.大庆石油学院学报，2007，31（6）：22－23.

Lyu Jing，Song Baoquan，Liu Jiyu.Method of geologic reserves division at the high water－cut stage［J］.Journal of Daqing Petroleum Institute，2007，31（6）：22－23.

［10］徐春华，范小秦，池建萍，等.面积权衡劈分方法计算单井地质储量［J］.特种油气藏，2005，12（2）：45－47.

Xu Chunhua，Fan Xiaoqin，Chi Jianping，et al.Calculate single well geological reserve by areal weigh split method［J］.Special Oil ＆Gas Reservoirs，2005，12（2）：45－47.

［11］霍春亮，刘松，古莉，等.一种定量评价储集层地质模型不确定性的方法［J］.石油勘探与开发，2007，34（5）：574－579.

Huo Chunliang，Liu Song，Gu Li，et al.A quantitative method for appraising reservoir geological model uncertainty［J］.Petroleum Exploration and Development，2007，34（5）：574－579.

［12］孙立春，高博禹，李敬功.储层地质建模参数不确定性研究方法探讨［J］.中国海上油气，2009，21（1）：35－38.

Sun Lichun，Gao Boyu，Li Jinggong.A discussion on the method to study uncertainty of geologic modeling parameters［J］.China Offshore Oil and Gas，2009，21（1）：35－38.

［13］薛艳霞，廖新武，赵春明，等.基于随机建模技术的油田开发初期河流相储层不确定性分析方法：以渤海A油田为例［J］.岩性油气藏，2012，24（1）：80－83.

Xue Yanxia，Liao Xinwu，Zhao Chunming，et al.Uncertainty analysis of fluvial reservoir in oilfield early development period based on stochastic modeling：a case study from A oilfield in Bohai Bay［J］.Lithologic Reservoirs，2012，24（1）：80－83.

［14］AKSHAY S.Case studies of uncertainty analysis in the seismic to reservoir simulation workflow［C］.SPE84188，2003.

［15］FRIEDMANN F，CHAWATHA，LARUE D K.Assessing uncertainty in channelized reservoirs using experimental designs［C］.SPE71622，2001.

An approximate method to breakdown the OOIP based on the OOIP－estimate parameter increments

Sun Lichun Jiang Baizhao He Juan Ni Jun’e Wang Hongqiang Guo Lina Wang Long
（CNOOC Research Institute，Beijing100028，China）

An analysis has been conducted on the pros and cons of the presently prevailing method to breakdown the OOIP increments（or changes）due to the variation of the OOIP－estimate parameters.The OOIP increments are estimated simply，and the contributions of all increments of relevant OOIP－estimate parameters are taken equally in the method，which is，shown in this study，not reasonable.The different impacts of the OOIP－estimate parameters on the OOIP increments should be fully regarded.So，a new approach is proposed with regard to this issue in which the nondimensionalization of the OOIP－estimate equation as well as all parameters is a prerequisite.Comparisons between these two approaches are conducted.The proposed approximate method is much more acceptable compared with the prevailing.The principle for the sensitivity and uncertainty studies is briefly discussed.The breakdown method for OOIP increments proposed in this study is much more practical and can be referenced in similar studies.

original oil in place（OOIP）；OOIP parameter；increment；approximate breakdown

TE155

A

2014－06－27改回日期：2014－10－13

（编辑：杨 滨）

1673－1506（2015）02－0048－05

10.11935/j.issn.1673－1506.2015.02.008

孙立春，1999年毕业于原成都理工学院，获油气田开发工程博士学位，现主要从事油气田开发地质、沉积学、油藏描述与储层地质建模、油气储量等方面的研究。地址：北京市朝阳区太阳宫南街6号院中海油大厦（邮编：100028）。电话：010－84522236。E－mail：sunlch＠cnooc.com.cn。