某火箭炮底架结构的拓扑优化设计

刘 晴，李 军，张 震，鲁霄光，丛龙腾

(1.南京理工大学 机械工程学院，南京 210094;2.湖北江山重工责任有限公司 研发中心，湖北 襄樊 441057)

远程多管火箭炮的底架是其功能结构的重要组成部分，目前各国对自己的装备部队都要求其具有快速性、应急性。因此在不降低武器系统使用性能的基础上，通过科学合理的技术手段来减轻其质量将是未来武器设计的一个重要发展趋势［1］。对该火箭炮底架进行结构设计，在保证其刚强度符合设计要求的前提下，以质量最轻为设计目标对其进行设计优化［2］，为该结构的减重研究提供了一套较为完整的优化设计方法。

1 底架结构与有限元建模

底架是火箭炮的重要组成部分，作为提供支撑的重要部件，其刚强度直接影响了火箭炮的性能。为了对底架结构进行新的设计，需要建立一个基底架三维模型。

在HyperMesh 中，采用的单位制为:mm、s、N、MPa、t(吨)。底架使用的材料的弹性模量为E=210 000 MPa、泊松比为min:f(x)=f(x1，x2，…，xn)

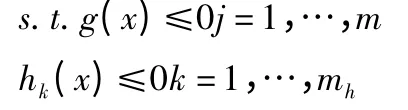
在底架的有限元分析中，由于简化后的有限元模型中，螺栓孔处的施力方式对整体优化结果影响不大［3-5］，因此在优化过程中将螺栓孔上的载荷按照等效节点载荷的形式施加在其内壁上。各支架采用刚性(RBE2)单元连接，其中主节点为孔中心面圆心，从节点为孔表面上所有网格单元节点。在前3 个工况下直接将力加载在各刚性单元连接的主节点上;由于工况4 所加为真实载荷故在工况4 下释放前支架刚性单元主节点的Y 轴转动自由度，约束其他自由度，同时释放左(右)支架刚性单元主节点的X 轴转动自由度，约束其他自由度。作用载荷是通过立轴止推轴承作用在座圈上传递给底架的，故在优化分析中将座圈上表面圆心作为载荷加载点，设置座圈上表面的所有节点与座圈上表面圆心的中点为柔性(RBE3)单元连接，其中主节点为座圈上表面的所有单元网格节点，从节点为座圈上表面圆心。在前3 个工况下约束柔性单元从节点的全部自由度，工况4 下在柔性单元从节点上施加座圈力。其中底架的有限元模型与各个工况的载荷及约束条件如图1 所示。

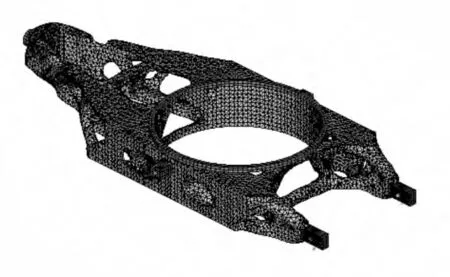
图1 底架有限元模型及各个工况下边界条件约束与载荷

2 底架结构初步拓扑优化

在HyperMesh 中的Optistruct 模块下，通过变密度法对底架在多工况下进行拓扑优化。设置的应力约束为150 MPa。所有工况的加权系数均为1［6］。体积分数上限为0.15。经过35 步迭代完成了该优化分析，优化后的底架质量为2.42 t，优化后底架在各工况下的最大位移与最大应力值情况见表1。对得到的优化模型进行OSSmooth 处理［7］，保留密度阙值为0.3 以上的单元，得到的优化结果有限元模型如图2 所示。

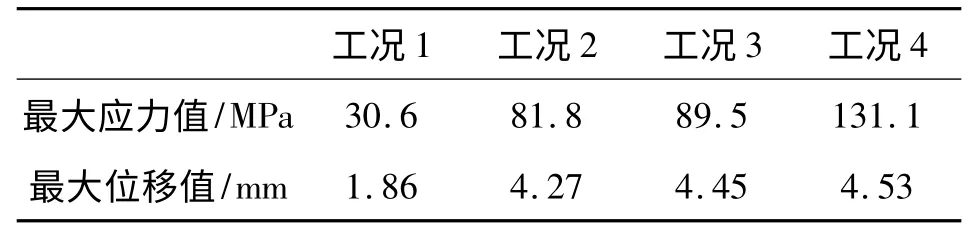
表1 初步拓扑优化后最大应力与最大位移值

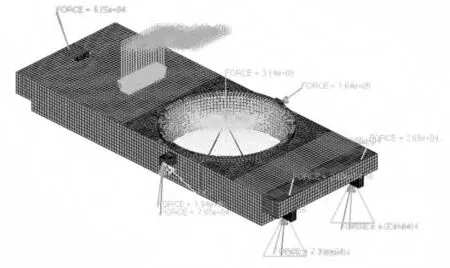
图2 初步拓扑优化结果有限元模型

3 底架结构二次拓扑优化

由于底架模型较为复杂，故还需进行二次优化。底架二次建模、网格划分好的有限元模型如图3 所示。此模型的边界条件、加载形式及优化设计参数均与初次优化模型相同，经过46 步迭代分析结束。表2 为优化后底架在各个工况下最大应力和最大位移的情况。

图3 二次拓扑优化有限元模型

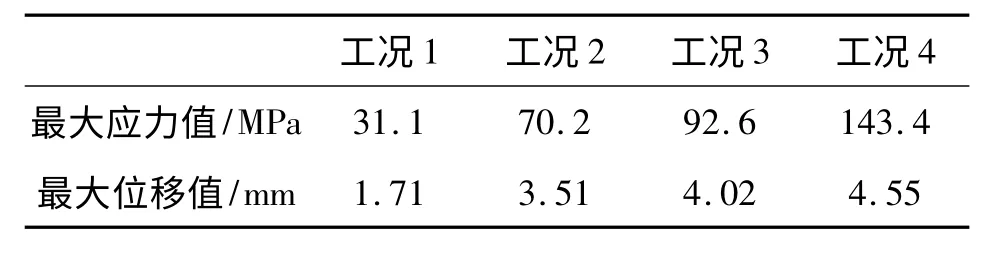
表2 二次拓扑优化后最大应力与最大位移值

二次优化后底架的质量由2.42 t 减小到1.62 t，下降幅度为34%，二次优化后底架前端结构类似于槽型梁结构，与底架的真实形状更为类似。保留密度阙值为0.3 以上的单元，对得到的优化模型进行OSSmooth 处理，得到的优化结果如图4 所示。

4 优化改进后底架性能分析

拓扑优化结果对底架结构进行整合与新设计，得到新的结构为薄板焊接结构，厚度均为6 mm。座圈与各支架的位置与优化模型所在位置相同，这里只对底架的主体结构重新进行了设计，整合拓扑优化结果得到的新模型如图5 所示。

图4 二次拓扑优化结果

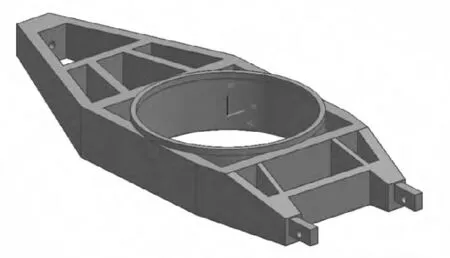
图5 新底架的三维模型

对模型进行有限元划分时，将其简化为2D 板壳单元［8］。新模型的边界条件、载荷加载与原始模型相同。新模型的质量为0.88t，较原始底架结构的1.15t 下降了29%，需要验证其结构是否符合性能要求。底架所用板材能承受的最大应力值为470 MPa，加上一定的安全系数，要求最大许用应力值不超过235 MPa［9-10］。这里仍然取4 个极限工况对模型进行静力分析，可知在前3 个工况下除了在个支撑部位即2D单元与3D 单元的连接处发生塑性变形，存在少量的应力集中，超过许用应力值以外，其余部位均符合设计要求;工况4下安装行军固定器的位置处的应力值较大，超出许用应力值，说明此部分设计有待加强。根据之前的设计经验底架最大变形量控制在30 mm 以内即满足设计要求，各工况下的最大变形量如表3 所示。

经过对底架的性能分析可以看出，底架质量在产生了明显下降后除了底架与支架的部位存在局部应力集中外，其余的底架变形量与最大应力均在许用范围之内。

表3 新底架各工况下的最大变形量

5 结论

综上所述，对某型火箭炮的底架进行了结构建模与优化设计，采用了两次拓扑优化的方法获得了底架的全新设计结构，比较了优化前后底架的使用性能，最终在不影响使用性能的前提下，又一次达到了轻量化的目的，为结构的优化改进工作提供了方向性的指导。

［1］杨树凯，朱启昕.基丁有限元技术的汽车支架拓扑优化设计研究［J］.汽车技术，2006(3):31-34.

［2］江爱川. 结构优化设计［M］. 北京:清华大学出版社，1986.

［3］周传月，腾万秀，张俊堂.工程有限元与优化分析实用实例教程［M］.北京:科学出社，2005.

［4］吕东升，王东方.基于HyperWorks 的某客车车架有限元分析［J］.机械设计与制造，2011(3):11-12.

［5］冯国胜，刘玉杰.基于神经网络的客车车身结构参数优化［J］.系统仿真学报，2006(2):54-59.

［6］M.Zhou，GIN.Rozvany.On the Validity of ESO Type Methods in Topology optimi zation［J］.Structure and Multidisciplinary Optimization，2001(21):80-83.

［7］董宇航.用HyperWorks 实现汽车车门的优化设计［D］.长春:吉林大学，2007:10-13.

［8］陈国华.基于有限元的汽车车门结构分析与研究［D］.南京:东南大学，2006:8-10.

［9］于开平，周传月，谭惠丰.HyperMesh 从入门到精通［M］.北京:科学出版社，2005.

［10］邹琳，于海昌，景俊鸿.6X4 自卸车车架有限元分析［J］.合肥工业大学学报，2007(12):44-47.