基于高阶非线性模型的铅酸蓄电池SOC估计

钟国彬，何 耀，刘新天，冯真得，苏 伟

（1. 广东电网公司电力科学研究院，广东 广州 510080；2. 合肥工业大学新能源汽车工程研究院，安徽 合肥 230009）

基于高阶非线性模型的铅酸蓄电池SOC估计

钟国彬1，何 耀2*，刘新天2，冯真得2，苏 伟1

（1. 广东电网公司电力科学研究院，广东 广州 510080；
2. 合肥工业大学新能源汽车工程研究院，安徽 合肥 230009）

摘要：铅酸蓄电池在电动汽车和蓄电池储能系统等领域有着广泛的应用，提高铅酸蓄电池荷电状态 (SOC) 估算的精度具有重要的意义。本文针对目前 SOC 估算方法中电池等效模型复杂、相关参数难以确定等问题，提出了一种新型高阶非线性拟合开路电压的 SOC 估计方法，通过拟合恒流充放电工况下的开路电压 (OCV)–SOC 曲线，建立适用于变电流充放电工况下的铅酸蓄电池模型，并结合扩展卡尔曼滤波算法 (EKF) 对电池的 SOC 进行估算。仿真和实验结果表明该方法能够实现铅酸蓄电池的高精度 SOC 估算。

关键词：铅酸蓄电池；充放电工况；荷电状态；开路电压；扩展卡尔曼滤波法；电动汽车；储能系统；高阶非线性

0　 引言

铅酸蓄电池的荷电状态 (SOC) 是反映其可持续供电能力的主要指标[1]。电池的充放电过程包含多种工况[2]，因此，进行适用于不同工况的电池 SOC精确估计算法的研究，对确保蓄电池稳定供电，延长电池的使用寿命具有重要意义[3]。扩展卡尔曼滤波算法 (EKF) 用 SOC 表征电池状态，将安时积分公式作为系统的状态方程[4]，其计算结果即为 SOC估算值；建立电池模型作为系统的观测方程，通过自动调节卡尔曼增益的方式降低观测变量的误差对系统状态的影响，达到滤波的效果，使状态方程的计算结果逼近实际的电池 SOC[5]。目前常用的电池模型结构复杂，需要通过对不同工况下的电池充放电曲线进行检测以确定相关参数，算法耗费时间较长，在实际工程应用中存在一定的局限性[6]。本文提出一种新型铅酸蓄电池 SOC 估算方法，通过拟合恒流充放电工况下的开路电压 (OCV)–SOC 曲线，建立适用于变电流充放电工况下的铅酸蓄电池模型，并结合 EKF 算法，对电池初始 SOC 估算误差和测量误差进行修正，从而精确估算电池的SOC，该方法所需参数变量易于采集，计算量较少，占用系统资源较少且不影响蓄电池的正常运行。

1　 适用于不同工况的统一铅酸蓄电池模型

1.1 恒流充放电模式下 OCV-SOC 高阶非线性拟合

根据 Mohamed Daowd 等提出的铅酸电池 PNGV模型，铅酸蓄电池开路电压与 SOC 存在着对应关系，可近似地通过高阶非线性方程进行拟合[7]，即

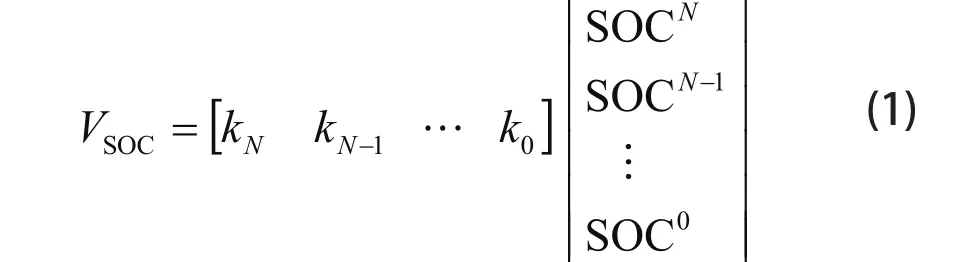
其中 N 为拟合的最高阶数，kN、kN-1…k0为拟合系数， Vsoc为测量到的电池实时开路电压，该模型的精确度与拟合的最高阶数 N 有关。

图 1 给出了 DJ100 铅酸电池 (2 V/100 Ah) 以0.1C 倍率放电各采样时间点的 OCV–SOC 曲线，其中曲线 1 为实测 OCV–SOC 曲线，曲线 2 为三阶拟合曲线，曲线 3 为五阶拟合曲线。可见，随着曲线拟合阶次的增加，放电曲线越来越接近电池的测量数据，但由于测量存在误差，拟合出的高阶曲线并不一定能反映电池的真实数值，而且随着拟合阶次的提高，系统运算量增加，不利于算法的实现[8]，不符合工程应用中的实时需求。因此本方法选择更精确的五阶模型，在保证估计精度的前提下较易实现。可得出该型号电池的五阶非线性 OCV–SOC 曲线的表达式（2）。由此可以确定拟合系数 k5、k4…k0的具体数值，通过恒流充放电下测得的 OCV–SOC 曲线建立适合复杂工况的电池模型。

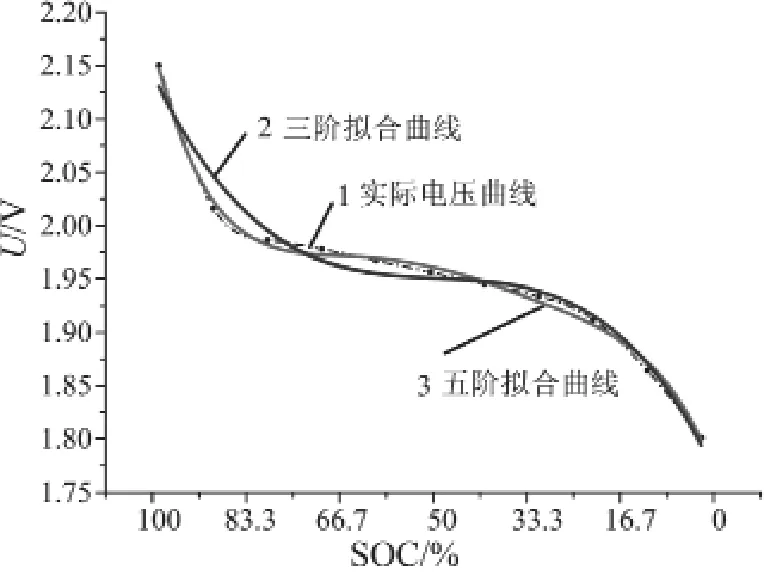
图 1 铅酸电池 OCV–SOC 曲线

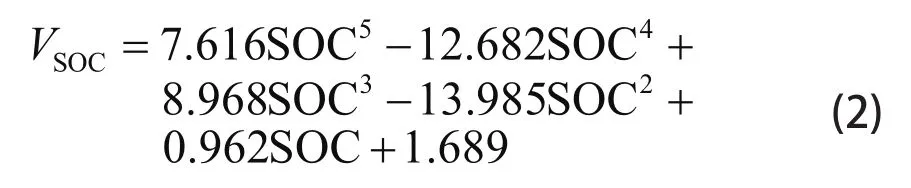
1.2 基于 OCV–SOC 曲线的铅酸电池建模

如果对铅酸蓄电池进行核对性放电，放电电流为 It，电池放电初始荷电状态为 SOC(t0)，则当前电池的荷电状态 SOC(t) 可由安时积分公式求得，即：

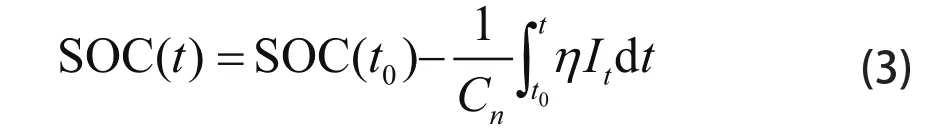
其中 Cn为电池额定容量， η 为库伦效率，放电时 η = 1，充电时 η ≤ 1。对上式进行欧拉逼近离散化处理得到电池 SOC 的状态方程为：

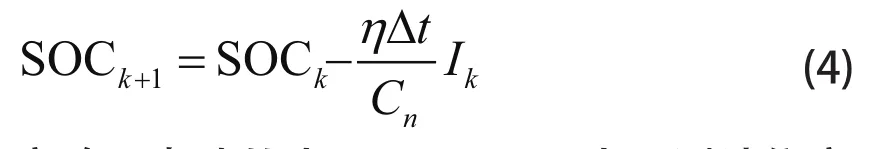
实验用电池的内阻用 HIOKI 内阻测试仪实时测量，初始电池内阻为 0.804 mΩ，放电末期的电池内阻为 0.816 mΩ。正常电池的整个放电过程的内阻变化范围不大，对 SOC 的影响可忽略不计，因此设定实验电池的内阻值 r 恒定，从而建立起电池系统非线性状态空间模型的观测方程：

2　 基于 EKF 滤波算法的电池 SOC 在线估计

铅酸蓄电池系统为典型的非线性系统[9]，基于上述的 OCV–SOC 模型，采用扩展卡尔曼滤波算法对设定的模型状态量进行迭代估算，算法模型的输入方程为

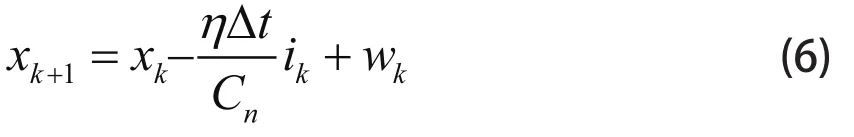
根据式 (3) 和 (5)，系统输出方程为

其中 xk表示第 k 次检测对应的 SOC ，yk为对应的电池端电压， ik为对应的充放电电流。设定系统先验估计均方误差为 Pk-，最优估计均方误差为Pk+，激励噪声 wk协方差矩阵为 Q，量测噪声 vk协方差矩阵为 R。定义系统状态矩阵 Ak为：

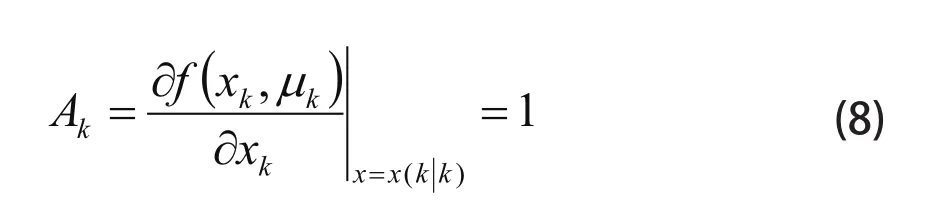
系统测量矩阵 Ck为：

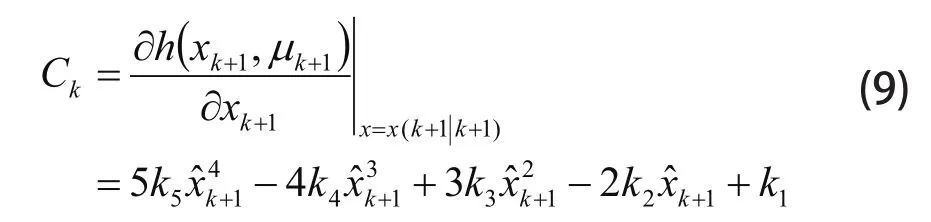
迭代过程如下：首先进行状态量、估计误差初始赋值，见式（10）；接着更新估计值时间、误差均方差时间，见式（11）；然后计算卡尔曼滤波增益，见式（12）；最后计算最优估计值、最优估计均方差，见式（13）。

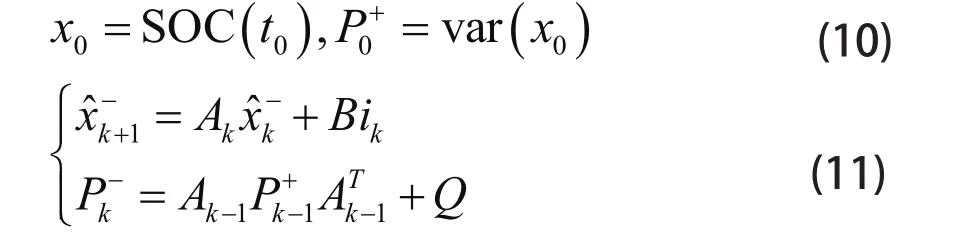
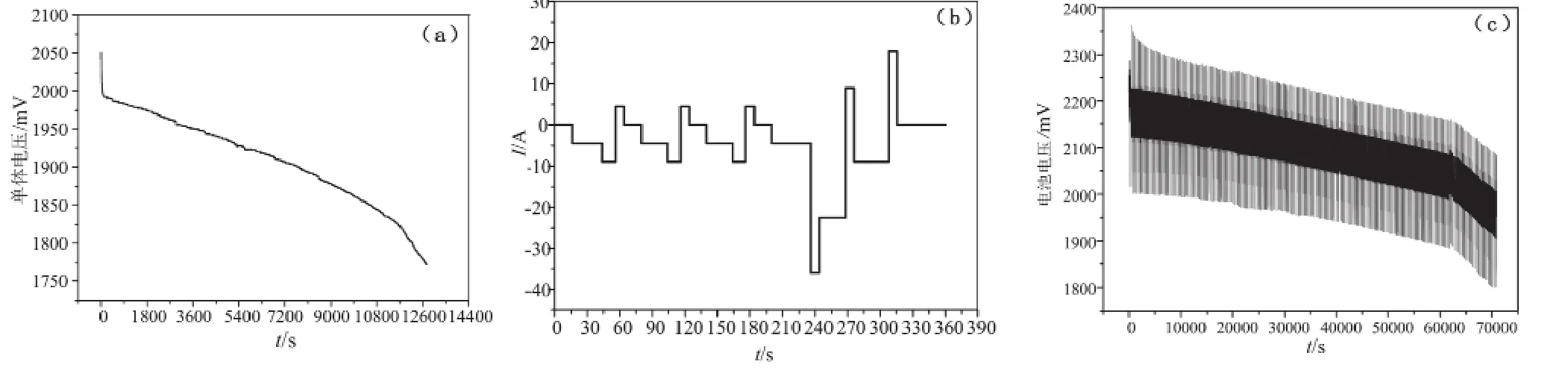
图 2 不同工况下的电池关键参数曲线

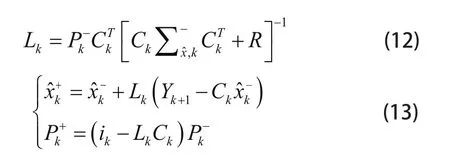
系统状态量的初始值 SOC(t0) 可根据当前电池开路电压值和前一次电池充放电的剩余电量得到。采用 EKF 算法来估算电池 SOC 值，实质上是用安时积分法来计算电池 SOC 的同时不断用检测的电池开路电压值 VSOC来对安时积分法算得的电池SOC 值进行修正[10]。当电池的初始 SOC 误差较大时，滤波增益矩阵 Lk的权值也大，对 SOC 的修正作用就强。反之，若电池的初始 SOC 误差较小，则 Lk的权值就小，对 SOC 的修正作用也就较弱。该方法可以有效地滤除系统噪声的影响，提升了电池 SOC 估计的精度。

3　 实验验证

3.1 实验条件及初始化参数设定

实验选用两只 2 V/100 Ah 铅酸电池串联，在25 ℃ 下，采用充放电机对电池组进行模拟实际工况试验，包括 0.2C 恒流脉冲放电试验和动态工况试验 (DST)。实验平台包括：电池组、充放电机、数据采集模块、BMS 系统及系统人机操作界面、电池测试系统上位机等。电池组充放电电流及电压数据由电池测试系统上位机实时监测保存，单体电压由 BMS 系统实时监测并实时显示。

将实验中保存的电池电流、电压等数据进行整理，采用数据分析软件得到不同工况下的电池关键参数曲线，如图 2 所示。其中图 2(a) 为 0.2C 恒流脉冲放电工况下的铅酸电池开路电压，图 2(b) 为DST 工况下电池电流波形，图 2(c) 为 DST 工况下的铅酸电池开路电压。从图中可以看出，DST 工况下的电池电压电流波形远比恒流工况下的复杂，采用所提出的模型进行 SOC 估算仅需要在恒流工况下进行测量，进而推广至复杂的工况，能够大幅度地减小测量工作和计算量。实验用铅酸电池通过恒流–恒压充电，计算得到电池初始 SOC(t0) 值为0.886，采样时间为 2 s，电池初始电压值为 2.051 V，误差协方差 P0= 1，系统噪声方差 Q = 0.1，量测噪声方差 R = 0.005。

3.2 估算结果验证

通过计算电池在某一段采样周期内释放的电量，基于构建的电池 OCV–SOC 模型。图 3 给出了0.2C 恒流工况下的基于构建的五阶电池 OCV–SOC模型和传统的三阶模型的 SOC 估计对比结果以及估计误差。由图中可以看出，针对恒流工况，本文提出的算法误差在 ±2 % 以内，而传统的三阶模型的误差接近 ± 5%，并呈发散趋势。

图 4 给出了 DST 工况下的基于构建的五阶电池OCV–SOC 模型和传统的三阶模型的 SOC 估计对比结果以及估计误差。由图中可以看出，针对 DST 工况，本文提出的五阶模型算法误差在 ±2 % 以内，而传统的三阶模型的误差超过 ±3 %，并呈发散趋势。

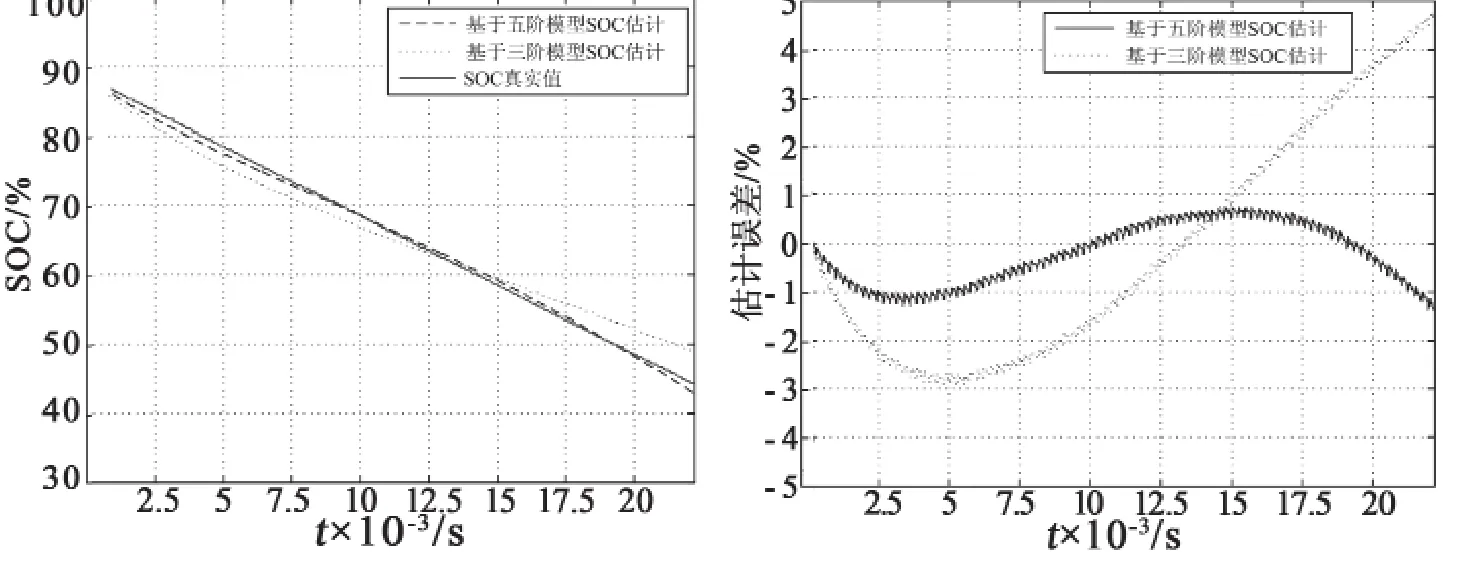
图 3 恒流工况下的电池 SOC 验证结果

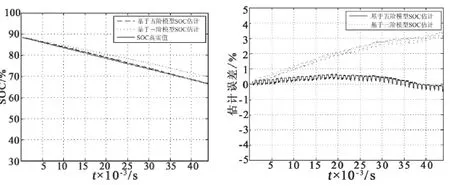
图 4 DST 工况下的电池 SOC 验证结果

4　 结论

本文在分析已有铅酸电池模型的优缺点基础上，提出采用高阶五次 OCV–SOC 模型来实现铅酸电池 SOC 估计，并采用扩展卡尔曼滤波算法对负载工况下铅酸电池 SOC 进行估计。仅需测量恒流模式下的电池充放电曲线，即可推广至复杂工况的实际应用中。所建立的铅酸蓄电池模型结构简单，参数易于确定，应用于 EKF 算法时计算量小。试验结果表明，所提出的 SOC 估算方法可以准确地预估铅酸蓄电池 SOC 的变化，估算误差在 ±2 %范围之内。在铅酸电池的实际应用中，同类电池相同工况下，电池 SOC 与环境温度存在一定的相关性，可进一步研究该 OCV–SOC 模型中拟合系数等参数与温度的关系，以适应不同温度条件下电池的 SOC 估算。

参考文献:

[1] Dufo López R, Lujano Rojas J M, Bernal Agustín J L. Comparison of different lead acid battery lifetime prediction models for use in simulation of stand-alone photovoltaic systems[J]. Applied Energy, 2014, 115: 242–253.

[2] 王坚, 吕荣冠, 焦昌梅. 电动汽车动力蓄电池充电及其管理的研究[J]. 蓄电池, 2012, 48(5): 230–236.

[3] 崔琼, 舒杰, 吴志锋, 等. 应用牛顿插值法估算铅酸蓄电池 SOC [J]. 电力电子技术, 2013, 47(7): 46–48.

[4] Xiong B, Zhao J, Wei Z, et al. Extended Kalman filter method for state of charge estimation of vanadium redox flow battery using thermaldependent electrical model[J]. Journal of Power Sources, 2014, 26(2): 50–61.

[5] Haykin S. Kalman filter and neural network [M]. New York: Wiley Inter Science, 2001.

[6] 刘新天. 电源管理系统设计及参数估计策略研究[D]. 合肥: 中国科学技术大学, 2011.

[7] 张利, 张庆, 常成, 等. 用于电动汽车 SOC 估计的等效电路模型研究[J]. 电子测量与仪器报, 2014, 28(10): 1161–1168.

[8] 伍双喜, 吴文传, 张伯明, 等. 电力系统仿真不确定度评估中拟合多项式阶次的确定[J]. 电网术2012, 36(10): 125–130.

[9] 穆婷. 直流供电电源系统阀控铅酸蓄电池剩余容量在线检测技术与应用[D]. 济南: 山东大学, 2004.

[10] 刘浩. 基于 EKF 的电动汽车用锂离子电池 SOC估算方法研究 [D]. 北京: 北京交通大学, 2010.

SOC estimation of lead-acid battery based on high-order-nonlinear fi tting model

ZHONG Guo-bin1, HE Yao2*, LIU Xin-tian2, FENG Zhen-de2, SU Wei1

(1. Guangdong Power Gird Corporation Electric Power Research Institution, Guangzhou Guangdong 510080; 2. New Energy Automobile Engineering Research Institute, Hefei University of Technology, Hefei Anhui 230009, China)

Abstract:Lead-acid batteries have been widely used in the fields of electric vehicles and battery energy storage systems. It is signifi cant to improve the estimation accuracy of state of charge (SOC) of them. The SOC estimation methods based on the current battery equivalent model are complex and diffi cult to determine the relevant parameters and other issues. This paper proposed a new high-order nonlinear fi tting open circuit voltage SOC estimation method. An alternating current charge-discharge lead-acid battery model which was fi tted for a constant current charge and discharge condition of the open circuit voltage (OCV)–SOC curve had been established. The SOC was estimated by combining with EKF algorithm. Simulation and experimental results showed that the proposed method did well in high precision lead-acid battery SOC estimates.

Key words:VRLA battery; charge and discharge condition; state of charge; open circuit voltage; EKF algorithm; electrical vehicle; energy storage system; high-order-nonlinear

中图分类号：TM 912.1

文献标识码：A

文章编号：1006-0847(2015)04-166-04

收稿日期：2015–02–15

基金项目：国家自然科学基金项目(21373074)；安徽省国际合作项目(1303063010)

*通讯联系人