碳纳米管质量传感器振动特性研究

陈越，李明林

(福州大学 机械工程及自动化学院, 福建 福州 350108)

碳纳米管质量传感器振动特性研究

陈越，李明林

(福州大学 机械工程及自动化学院, 福建 福州 350108)

基于欧拉-伯努利梁理论对单壁碳纳米管质量传感器的振动特性进行研究。分别考虑悬臂梁式和两端固定式碳纳米管质量传感器，研究吸附质量对其谐振频率漂移的影响。推导出任意位置的吸附质量下，碳纳米管质量传感器的等效刚度、等效质量和谐振频率的解析表达式，推导出传感器的非线性应用方程及其简化形式。在特定位置下吸附质量对不同长度碳纳米管谐振频率的影响进行了研究。数值仿真结果表明，对于不同的边界约束和特定的吸附位置条件下，吸附质量越大、碳纳米管的长度越短，导致的碳纳米管频率漂移越大。对于8 nm长的碳纳米管，在悬臂式约束下，吸附质量越远离固定端，引起的频率漂移越大。而在两端固定约束下，则是吸附质量越靠近固定端，频率漂移越大。揭示了传感器的谐振特性，有助于促进碳纳米管在纳机谐振器领域的推广应用。

单壁碳纳米管；质量传感器；欧拉-伯努利梁理论；谐振频率

0 引言

近20年来，微纳米悬臂梁作为一类新型的传感器已在物理、化学和生物等领域获得广泛的关注和研究。其发展目标之一是不断提高和突破对待测物理量的检测极限。例如，1994年Barnes[1]就首次用微米复合悬臂梁将传统热量计的检测极限由约10-8W提高到10-10W量级。2000年，Fritz[2]首次展示利用硅微米悬臂梁阵列检测单个碱基错配的试验范例，其检测浓度极限可达10-8Mol。2001年，Ilic[3]根据质量吸附引起硅微米悬臂梁谐振频率的漂移测出单个E.coli细菌的质量(665×10-12g)。随着悬臂梁尺寸的缩小，特别是碳纳米管的引入，使得单个原子质量分辨率的检测能力得以提高[4-6]。然而，关键的问题是如何定量描述待测物理量与系统频率响应之间的关系。

考虑到碳纳米管的尺度效应，Hwang[7]研究团队针对多种质量吸附方式，利用分子动力学模拟研究了碳纳米管谐振运动的漂移效应。作者团队[8]也曾利用分子结构力学方法和分子动力学模拟方法研究过苯环分子吸附在碳纳米管外壁时引起的谐振频率漂移特性。考虑到工程应用的实用性，基于欧拉-伯努利梁理论的碳纳米管谐振运动方程具有简洁的解析表达式，Chowdhury[9]等人推导出特定吸附位置下，碳纳米管谐振特性与吸附质量间的实用性工程应用关系。然而，吸附位置的变化对谐振频率漂移影响则尚未得以深入研究。

文中以碳纳米管作为传感器检测吸附质量大小，质量检测的原理是谐振频率对谐振器质量(谐振器质量包括谐振器自身质量和附加物质量)变化的敏感性，谐振器上附加微小质量的改变引起其频率漂移。对于吸附物引起碳纳米管固有谐振频率变化的研究，连续体力学模型常将附着物的质量等效为作用于梁上的外加载荷[8]，现将以悬臂式和两端固定式单壁碳纳米管分别进行研究，运用连续介质力学理论推导出任意位置的吸附质量下，碳纳米管质量传感器的等效刚度、等效质量和谐振频率的解析表达式，并推导出传感器的非线性应用方程及其简单线性近似和立方近似。此外，对碳纳米管长度在1nm～1μm范围内，特定位置的吸附质量对谐振频率的影响进行研究。此理论研究工作将为纳机械质量传感器的器件设计和性能优化提供必要的理论指导。

1 单壁碳纳米管附加质量的谐振频率

连续体介质理论在研究单壁碳纳米管中得到广泛的运用,连续介质力学模型常将附着物的质量等效为作用于梁上的附加载荷，适用于本研究模型。为了得到附加质量的简单解析表达式，应用欧拉-伯努利理论把单壁碳纳米管简化为梁模型，自由振动的运动方程为：

(1)

式中：E为杨氏模量，I是截面二次矩，ρ和S分别为材料的密度和截面积。

根据单壁碳纳米管的边界条件和附加质量位置，可以推导出系统的谐振频率。在此只考虑基频，可以描述为：

(2)

其中：keq和meq分别为一阶振动形式单壁碳纳米管上吸附质量的等效刚度和等效质量。有吸附质量与无吸附质量时，系统产生的频率漂移情况将被研究。

1.1 吸附质量位置在距固定端长度为a的悬臂梁式单壁碳纳米管

假设吸附质量为M，碳纳米管长度为L，吸附质量位置距固定端长度为a，如图1，给定在附加质量位置的一个虚拟力，使碳纳米管产生一个单位位移。这种假设可见于文献[10]。

图1 吸附质量位置在距固定端长度为 a的悬臂梁式单壁碳纳米管

梁模型挠曲线方程为：

令吸附质量作用下产生的挠度为单位长度1，此时等效刚度为：

(3)

在y轴方向的位移方程为：

将梁的位移曲线方程Y(x)作为近似振型，假设简谐运动y(x,t)=Y(x)exp(iω0t),ω0为系统的固有角频率,则得出系统的动能为：

可得出等效质量为：

(4)

代入方程(2),

(5)

可得出谐振频率为：

(6)

当没有吸附质量，也就是式(6)中ΔM=0时，

fom=α

(7)

结合式(6)式(7)，谐振频率可以写为：

(8)

1.2 吸附质量位置在距左端长度为a的两端固定梁式单壁碳纳米管

假设吸附质量为M，碳纳米管长度为L，吸附质量位置距左端长度为a，如图2，给定在附加质量位置的一个虚拟力，使碳纳米管产生一个单位位移。这种假设可见于文献[10]。

图2 吸附质量位置在距左端长度为 a的两端固定梁式单壁碳纳米管

梁总长度L=a+b，此结构为二次超静定结构，把固定端A看成由一个支反力RA和一个弯矩MA合成，A端处挠度和转角都为零。

在距A端x3处的界面挠度方程为：

在距A端x4处的界面梁模型挠度方程为：

令载荷作用下产生的挠度为单位长度1，此时等效刚度为：

(9)

在y轴方向的位移方程为：

Y2(x)=-

代入b=L-a,得出动能为:

等效载荷为:

(10)

代入式(2)可得出谐振频率为：

(11)

(12)

其中：

当没有吸附质量，也就是方程(12)中ΔM=0时，f0m通过以上方程可以得到由于频率改变而测出附加的质量大小。

2 传感器方程的一般表达式推导

本节推导了通过单壁碳纳米管频率变化检测吸附质量大小的一般表达式，一般表达式的推导有助于促进碳纳米管在纳米机械谐振器领域的进一步推广应用。结合式(7)式(8)，频率变化可以描述为：

(13)

由此可以得出：

(14)

此方程反映了频率变化与吸附质量之间的关系。把式(14)泰勒展开可得：

(15)

因此，保留第一项和保留前3项就变成线性近似和立方近似：

(16)

(17)

单壁碳纳米管吸附质量与频率变化之间的关系如图3。式(15)中的精确解将与式(16)线性近似和式(17)立方近似对比分析。

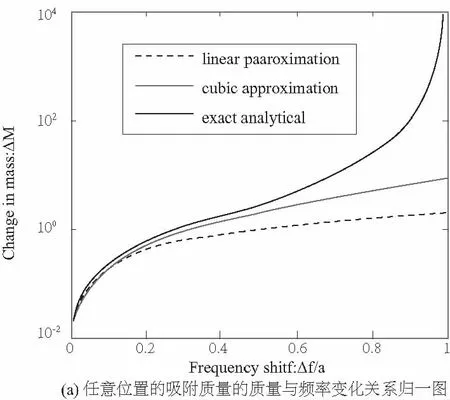
图3 单壁碳纳米管吸附质量与频率变化关系归一化图

由图3可知, 任意位置的吸附质量的质量与频率变化关系图3(a)与吸附质量位置在端点和中点的质量与频率变化关系图3(b)图形基本一致。

综上可知，无量纲常数α与边界条件有关，悬臂式与两端固定式单臂碳纳米管有着相似的质量与谐振频率变化规律，并且不同位置的吸附质量有着相同的质量与谐振频率变化规律。

3 推导的公式与三维图分析

3.1 悬臂梁式单壁碳纳米管模型

3.1.1 吸附质量在距固定端长度为a的位置

选取的单壁碳纳米管主要参数如下:

E=1.0Tpa

L=8nm

ρ=2.24g/cc

D=1.1nm

d=0.5nm

谐振频率方程为:

把选取参数代入后,以a为x轴,范围是1～8nm(因为0～1nm范围内梁模型误差较大，并且在微观环境下极其靠近固定端时附加载荷位置难以控制。以下模型的长度范围选择依据同上),步长为0.08nm;以M为y轴,范围是0～8×10-22kg,步长为8×10-25kg,得出的位置a、质量M与频率变化Δf之间的关系如图4:

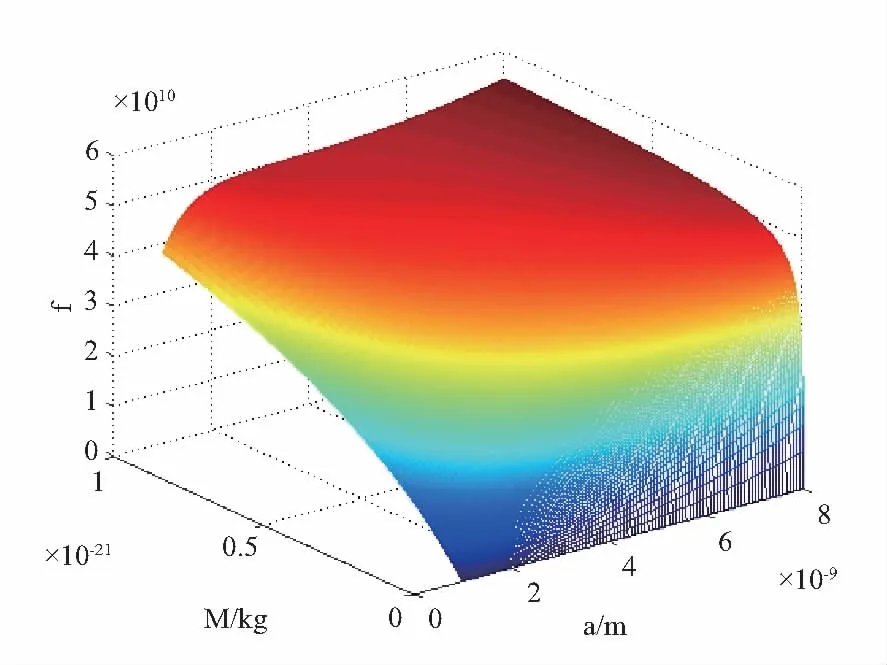
图4 吸附质量在距固定端长度为a的位置的悬臂梁式 单壁碳纳米管位置a、质量M与频率变化Δf之间的关系图

从图4中可以看出，当碳纳米管长度为8nm时，位置a、质量M的改变对频率Δf影响明显，且随着a、M的增大Δf的值增大，在自由端处达到最大值,即吸附质量加载在自由端,频率变化量最大,最佳测量位置即灵敏度最高的位置为自由端。这与式中M和a与Δf的变化规律相一致。

3.1.2 吸附质量在端点(a=L时)

对长度L在1μm到1nm的范围内与质量和谐振频率的关系进行研究,其余参数不变,纳米谐振频率方程变为:

(18)

把选取参数代入后,以L为x轴,范围是1μm～1nm,步长为1nm;以M为y轴,范围是0～10～22kg,步长为10-25kg,得出的长度L、质量M与频率变化Δf之间的关系如图5。

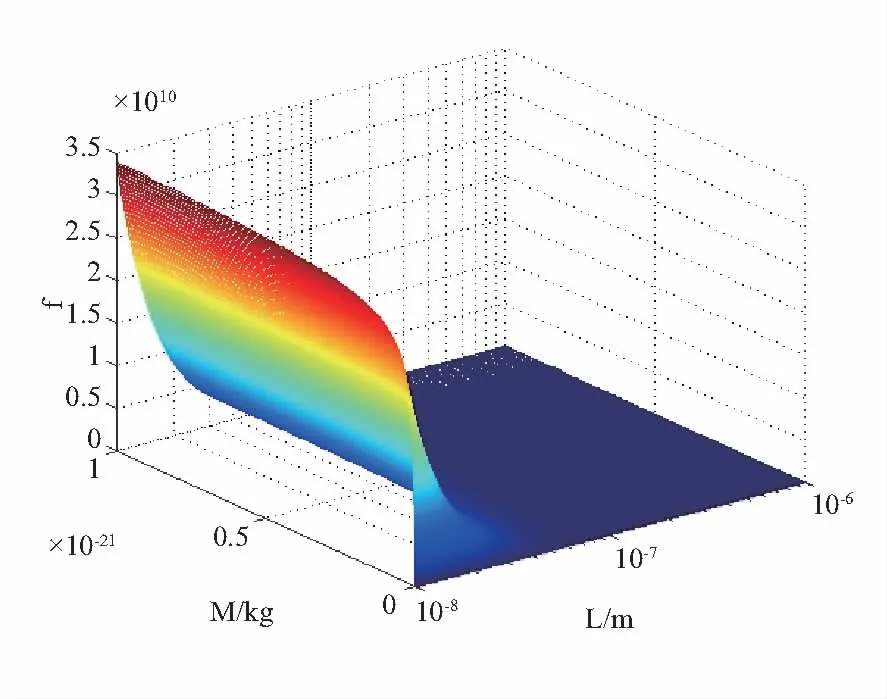
图5 吸附质量在悬臂梁式单壁碳纳米管端点(a=L时) 位置a、质量M与频率变化Δf之间的关系图

从图5中可以看出，碳纳米管的长度L、质量M的改变对频率Δf影响明显，随着L的减小Δf的值增大，长度L在接近1nm时有个陡增的过程；而随M增大Δf的值增大，而M增量比较平缓。

3.2 两端固定式单壁碳纳米管模型

3.2.1 吸附质量在距左端长度为a的位置

谐振频率变化方程为:

(18)

把选取参数代入后,以a为x轴,范围是1～7nm,步长为0.08nm;以M为y轴,范围是0～8×10-22kg,步长为8×10-25kg,得出的位置a、质量M与频率变化Δf之间的关系如下图6。

图6 吸附质量在距左端长度为a的位置的桥式 单壁碳纳米管位置a、质量M与频率变化Δf之间的关系图

从图6中可以看出，当碳纳米管长度为8nm时，图形关于梁中间位置(图中4nm处)对称,当a取在中间位置时Δf最小,向两侧固定端逐渐增大，随着M的增大Δf的值增大。

3.2.2 吸附质量在中点(a=L/2时)

对长度L在1μm～1nm的范围内与质量和谐振频率的关系进行研究,其余参数不变,纳米谐振频率方程变为:

(19)

把选取参数代入后,以L为x轴,范围是1μm～1nm,步长为1nm;以M为y轴,范围是0～10～22kg,步长为10-25kg,得出的长度L、质量M与频率Δf之间的关系如图7。

图7 吸附质量在两端固定式单壁碳纳米管中点 (a=L/2时) 位置a、质量M与频率变化Δf之间的关系图

可见，碳纳米管的长度L、质量M的改变对频率Δf影响明显，随着L的减小fn的值增大，长度L在接近1nm时有个陡增的过程,随M增大Δf逐渐增加。图5和图7变化规律十分相似,说明悬臂梁式与两端固定式单壁碳纳米在边界条件不同的情况下,随长度的变化有相似的谐振频率变化规律。

4 结语

介绍了基于连续介质力学理论的单壁碳纳米管作为质量传感器的一种研究方法。以悬臂式和两端固定式单壁碳纳米管分别进行研究，推导了单壁碳纳米管上任意位置的附加载荷与其谐振频率的联系方程和非线性谐振方程的简单线性近似和立方近似，以及位置、质量、谐振频率之间的图像分析。对碳纳米管长度在1nm～1μm范围内，特定位置的附加载荷对谐振频率的影响进行研究。结果表明，对于不同的边界约束和特定的吸附位置条件下，吸附质量越大、碳纳米管的长度越短，导致的碳纳米管频率漂移越大。对于8nm长的碳纳米管，在悬臂式约束下，吸附质量越远离固定端，引起的频率漂移越大。而在两端固定约束下，则是吸附质量越靠近固定端，频率漂移越大。新型传感器谐振方程运用在基于生物传感器的碳纳米管上具有更广泛的实用性。

[1] Barnes,J. R.，Stephenson R. J.,Welland M.E., et. al. Nature. 1994, 372,79.

[2] Fritz J.，Baller M. K.，Lang H. P., et. al. Science, 2000, 288, 316.

[3] llic B.，Czaplewski D., Zalalutdinov M.，et. al. J. Vac. Sci. Technol. B, 2001, 19 (6)，2825.

[4] Jensen, K., Kim, K. & Zettl, A.，Nat. Nanotech.，2008, 3, 533-537.

[5] Lassagne, B. , Garcia-Sanchez, D.，Aguasca, A. et. al. Nano Lett.，2008,8(11)，3735-3738.

[6] Chiu, H. -Y., Hung, P., Postma, H. W. Ch. et. al. Nano lett.，2008, 8(12)，4342-4346.

[7] Wang, D.H., Wang, G.F., J. Nanomater. 2011, 2011, 12.

[8] 李明林,叶伟,杨晓翔.分子化学吸附对碳纳米管谐振频率的影响[A]. 第十二届全国物理力学学术会议,CSTAM(2012)D01-0089.

[9] R. Chowdhury ,S.Adhikari , J.Mitchell, Vibrating carbon nanotube based bio-sensors[J]. Physica E 42 (2009) 104-109.

[10] J.E. Shigley, Mechanical Engineering Design, McGraw-Hill, USA, 1988.

Investigation on the Vibration of Carbon Nanotube Based Mass Sensors

CHEN Yue,LI Minglin

(School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China)

Vibrational properties of single-walled carbon nanotubes (SWCNTs) as a mass sensor is examined using Euler-Bernoulli beam theory based approach. In order to figure out how the attached mass affects the resonant frequency of the carbon nanotube resonators, the resonators both in bridged and in cantilevered configurations are studied. Firstly, analytical formulas of equivalent stiffness, equivalent mass and resonant frequency are developed for CNT-based nanoresonators with attached mass at any location. In addition, a simplified form of the nonlinear sensor equation and image analysis of the relationship among load location, the attached mass and resonant frequency have been investigated. Then for different lengths of SWCNTs, the influence of the attached mass in a specific location on the resonant frequency has been derived. The simulation results indicate that in the condition of different boundary constraints and the specific adsorption location, the heavier attached mass and shorter carbon nanotube is,the greater frequency drift will be. As for the nanotube of 8nm, the attached mass which is farther away from the fixed boundary causes the greater frequency drift in cantilevered. While the attached mass closer to the fixed boundary causes the greater frequency drift in bridged. The results illustrate that the new vibrational properties can be used for CNT-based mass sensors for further promote application.

SWCNTs, Mass sensor, Euler-Bernoulli Beam Theory, Resonant frequency

国家自然科学青年科学基金课题(50903017)

陈越(1987-)，男，湖南长沙人，硕士研究生，研究方向为固体力学。

TP212

A

1671-5276(2015)05-0171-05

2014-03-04