单边磁拉力对大型感应电机转子临界转速的影响分析

孟大伟，施道龙，于喜伟，刘慧敏（哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080）

单边磁拉力对大型感应电机转子临界转速的影响分析

孟大伟，施道龙，于喜伟，刘慧敏
（哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080）

以11kV、20极6500kW大型三相感应电机为例，研究单边磁拉力对大容量低速电机转子振动的影响。采用有限元法计算出转子的单边磁拉力；运用软件ARMD（Advanced Rotating Machinery Dynamics）建立了该大型三相感应电机转子动力学模型；以对模型是否填加单边磁拉力作为边界条件，分别计算得出转子前三阶固有频率。通过对比分析数值计算结果可知，单边磁拉力的存在会使转子固有频率降低，而增大轴承支承刚度有利于消除这一影响。由此为大型感应电机转轴机械设计进而提高其运行性能及可靠性，提供了理论依据。

有限元法；单边磁拉力；ARMD；转子动力学；固有频率

0 引言

电机的噪声和振动是衡量一台电机性能的重要指标，也直接关系到电机的质量和使用寿命[1]。电机转速接近临界转速时，电机将产生共振现象。理论上振幅会增加到无穷大，但实际由于在阻尼因素的作用下振幅是有限的，但当振幅增加到一定程度时，将使相关零部件磨损加速，噪声增大，甚至使转轴断裂，降低机组的可靠性。这就需要很好地研究电机中各重要零部件对临界转速的影响，根据电机实际运行情况，计算电机转子临界转速的变化趋势，判断是否发生共振，提出合理的结构设计避免共振现象的发生[2]。

实际上影响电机转子临界转速的因素有很多，例如轴承支座的柔度、转子质量的回转效应、单边磁拉力和轴上各种零件与轴的配合等等。由于制造质量或安装不当，使定转子之间气隙的不均匀产生单边磁拉力。单边磁拉力对电机的运行产生较大的影响，将会导致系统产生振动和噪声[3]。本文所分析的样机YZYKK1800-20 11kV 6500 kW是目前世界上容量最大的20极感应电动机。由于其特殊的应用场合，研究不平衡磁拉力对其转子系统振动的影响是十分重要的。通过磁场分析计算电机的单边磁拉力，运用ARMD建立考虑单边磁拉力的转子振动模型，计算出临界转速与轴承支承刚度变化曲线，分析单边磁拉力对转子临界转速的影响，对该电动机的转轴设计及可靠性分析提供一定帮助。

1 单边磁拉力分析与计算

1.1 气隙磁密计算

分析样机的参数如表1所示，定、转子槽型及尺寸如图1所示。

表1 样机主要参数

图1 定、转子槽型图

考虑对临界转速影响最不利情况，假定转子在垂直方向发生偏心e0=0.1δ，如图2所示。

图2 转子偏心示意图

对于单边磁拉力计算，主要需要考虑气隙中磁场分布，因此可忽略端部效应，求解二维场。偏心后模型如图2所示，假定[4-8]：

（1）电机磁场沿轴向均匀分布，电流密度J和矢量磁位A只有轴向分量，即J= Jz，A= Az；

（2）铁心冲片材料各向同性，且磁化曲线是单值的，即忽略磁滞效应；

（3）电机机壳外部和转轴内磁场忽略不计，即定子外表面圆周和转子内表面圆周为一零矢量位面；

（4）忽略铁心的涡流效应。矢量磁位A控制方程为：

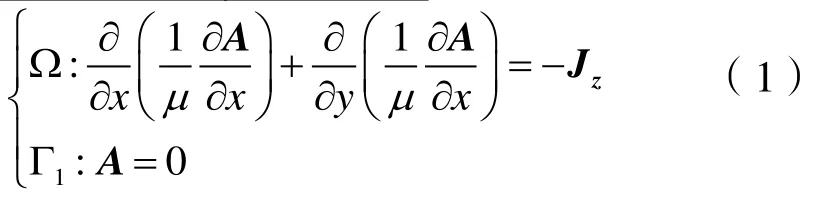
式中Ω为解区域，Γ1为定子外圆和转子内圆边界，JZ为外加轴向电流密度矢量，μ为磁导率。

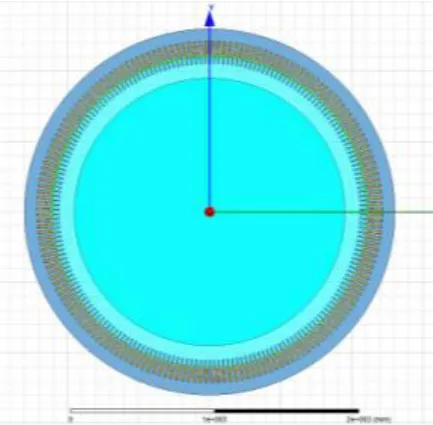
图3 转子偏心后样机2D模型

采用有限元法对电机气隙磁密进行求解，幵经过相应处理，得到转子偏心后电机负载气隙磁密波形图，如图4所示。

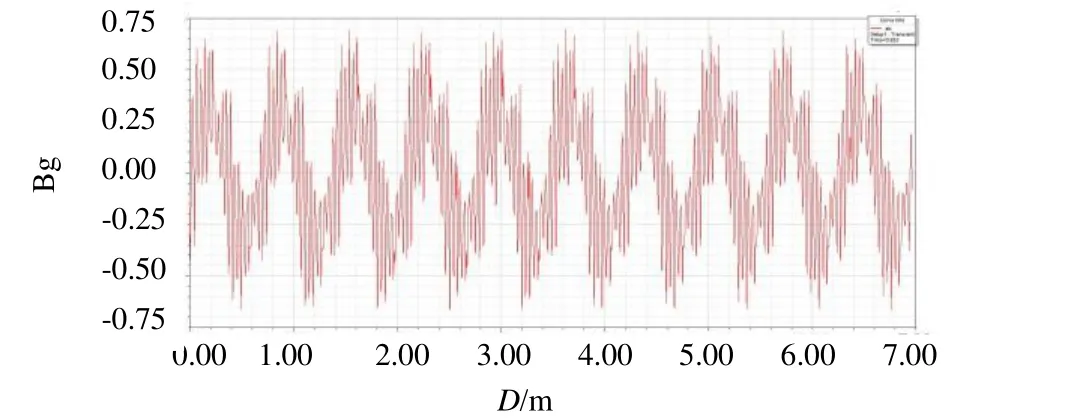
图4 转子偏心后气隙磁密曲线图

1.2 单边磁拉力的计算

根据电磁铁对衔铁的吸力公式：

式中B为电磁铁与衔铁间平均气隙磁密，A为电磁铁一个极的表面积，μ0为真空磁导率。

转子仅在垂直方向发生偏心e0，取电机气隙任一直径上的一对极，该对极的轴线和铅垂线成θ角，且偏心按余弦函数变化，气隙磁密由Bδ变为Bδ1和Bδ2，式中Bδ1为大气隙侧的磁密，Bδ2为小气隙侧的磁密。忽略饱和及因气隙变化而引起气隙系数的变化。由公式（2）可知这对极产生的单边磁拉力为：

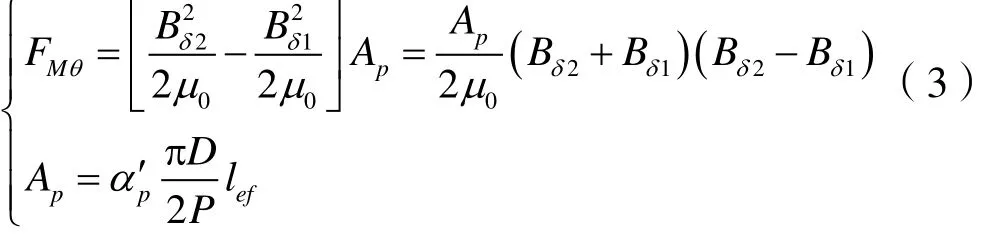
式中Ap为一个极表面积，α′p为计算极弧系数，D为电枢直径既定子内径，lef为电枢的计算长度，p为极对数。

进一步考虑电机类型、磁场分布、饱和、槽、阻尼和绕组结构等的不同影响后，式（3）可写成：

式中，β为经验系数，样机为感应电机，取β=0.3。

此磁拉力在铅垂方向的分力为FMθcosθ。考虑样机所有对极的磁拉力后，显然，转子仅在铅垂方向受力，则总的单边磁拉力为：

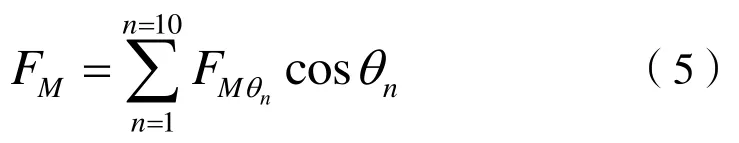
式中，FMθ为第n对极所产生的单边磁拉力，θn为该对极的轴线和铅垂线所成角度。

由图4读出所有极下平均气隙磁密，由式（5）求得计算样机的单边磁拉力为182087.42N。

2 单边磁拉力对转子临界转速的影响

2.1 转子—轴承系统模型的建立及边界条件

转子—轴承系统模型（含半联轴器部分）的建立是将质量连续分布的弹性转子抽象化为由不计厚度但计及惯量的刚性圆盘和不计质量但计及刚度的弹性轴段组成的盘轴系统。转子动力学的有限元模型假定[9]：

（1）圆盘是有质量和转动惯量而无厚度、无变形的刚性薄圆盘；

（2）轴段是有刚度和长度而无质量的弹性轴。

样机转子—轴承有限元模型在横向上分为42个单元，转子铁心部分简化成包含质量和转动惯量的圆盘，均匀分布在转轴的铁心段；圆盘和半联轴器部分用不同颜色来区分；对于支撑转子的轴承，可以转化为各向同性的转子支撑，本模型用2根弹簧来反映系统的刚度和阻尼。简化后模型如图5所示，整个系统的物理参数如表2。转子的结构和质量确定后，其自由振动的固有频率随之确定[10]。

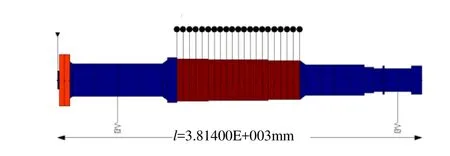
图5 样机转子—轴承系统有限元模型

表2 样机转子—轴承系统参数

转子模型采用 Jeffcott 模型。它包含一个无质量的转轴，转轴中间有一质量为m的圆盘，圆盘的质量偏心距为a。系统的横向振动微分方程为[11]：

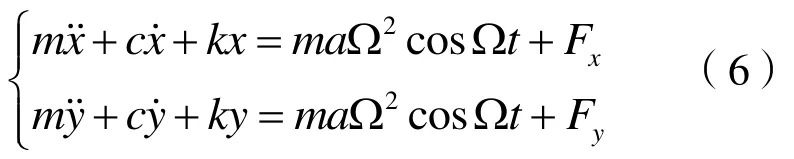
式中，m为转子质量，c为阻尼系数，k为弹性系，Ω为旋转转速，Fx、Fy为单边磁拉力在x、y方向的水平分量。

2.2 临界转速的计算

在影响转子系统动态性能的多种因素中，轴承的作用极为关键，所以转子动力学通常也称为转子—轴承动力学。研究发现轴承刚度的大小对转子系统的临界转速及振型影响非常大；实际应用时转子系统的轴承刚度变化范围也很大，如滚动轴承与滑动轴承的刚度差别；另一方面，即使选用刚度较大的滚动轴承，轴承预紧力不同，轴承刚度也不同；再有，轴承刚度在转子运行过程中是动态变化的，通常表现为轴承刚度随着转速的升高而降低，即所谓的旋转软化现象[12]。因此，轴承刚度对整个转子系统的影响十分重要。基于此，重点分析不同轴承的径向刚度对转子系统的模态影响。

2.2.1 不考虑单边磁拉力转子临界转速的计算

样机转轴的材料为45号锻钢，弹性模量为2.09×1011Pa，泊松比为0.3，密度为7890kg/m3。不考虑单边磁拉力时，计算得到转子固有频率随支承刚度变化的曲线如图6所示。

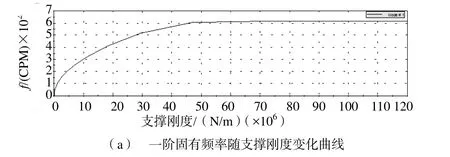
2.2.2 考虑单边磁拉力转子临界转速的计算

电机在实际运行时不可避免地会产生单边磁拉力。将单边磁拉力以与转子重力同方向附加以后，样机转子—轴承系统的固有频率随支撑刚度变化曲线如图7所示。

可以发现随轴承径向刚度逐渐升高，转子—轴承系统的临界转速也逐渐升高，即共振点逐渐增大，说明选用高刚度的轴承可以避免发生共振现象。样机的额定工作转速为297r/min，可以看出，当轴承刚度在2.0×107N/m附近时，转子系统工作频率与系统的固有频率已经非常接近，因此要注意轴承刚度变化对转子—轴承系统固有频率的影响。

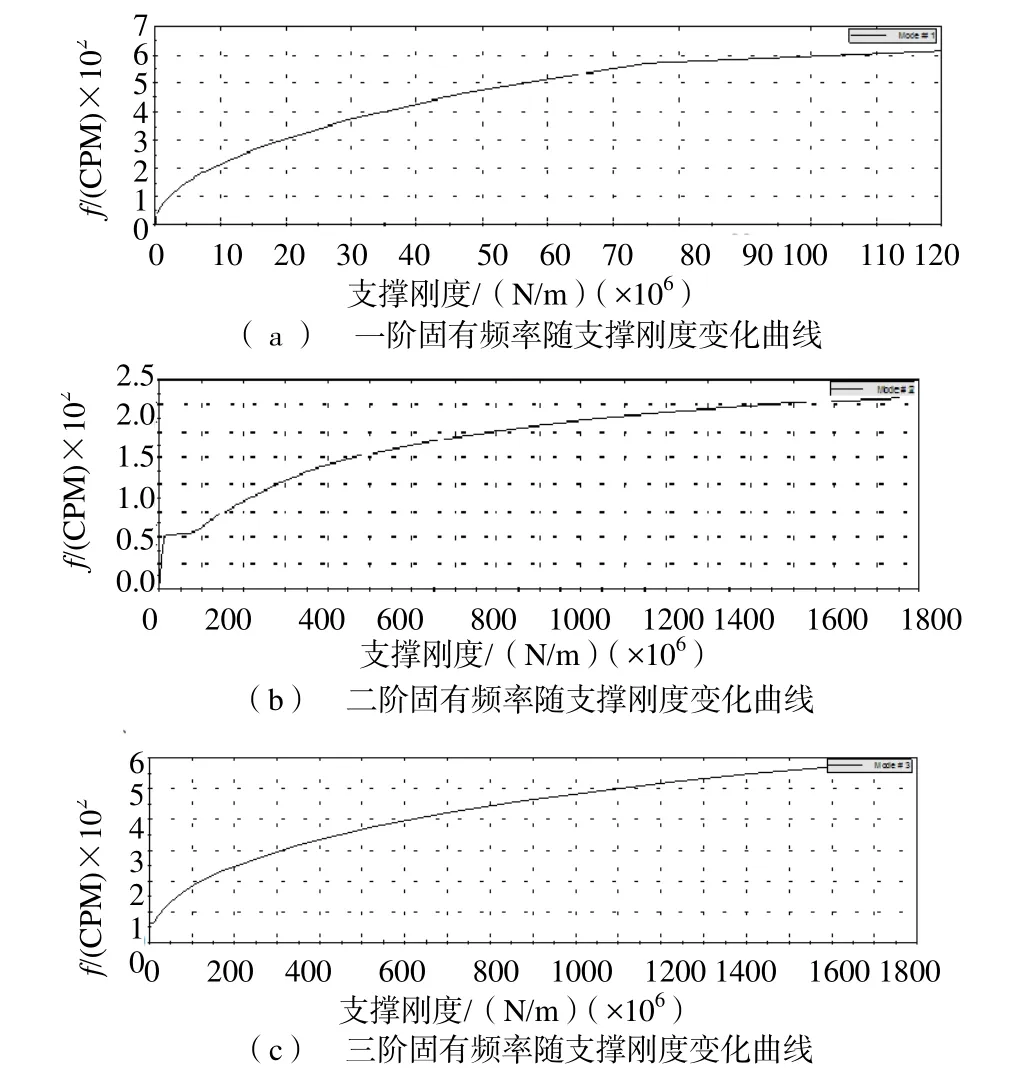
图7 考虑单边磁拉力转子前三阶固有频率

分析振型可以得到与之相对的固有频率下转子结构的变形趋势，从而为下一步的转子动力学分析，如转轴动平衡分析提供理论依据。计算出的转子前三阶振型如图8所示。

图8 考虑单边磁拉力转子前三阶振型

可以看出，考虑单边磁拉力时，转子中心轨迹增大。一阶临界转速下转子产生小幅偏心，二阶与三阶临界转速下的转子产生的偏心较一阶临界转速下产生的偏心大得多，因此电机轴承受力很大。若在该二阶与三阶临界转速下持续运行则会因转子偏心过大，使电机轴承磨损增加，损坏加快。

2.3 对比分析

固有频率可以通过公式（7）近似计算为相应的临界转速值：

式中，f为振动频率/Hz，n为转速/(r/min)。

选取不同轴承支撑刚度下临界转速对比如表3所示。可以看出，单边磁拉力对一阶临界转速的影响较大；且在低刚度段，单边磁拉力使转子—轴承系统的固有频率明显降低，即临界转速降低，但在轴承支撑刚度增大到108(N/m)数量级以上时，单边磁拉力对临界转速的影响可以不计。由此可知，增大轴承刚度能有效减少单边磁拉力的影响，因此轴承设计要综合考虑单边磁拉力对临界转速的影响。合理的支撑刚度既可以节约成本又可以减少事故发生率，延长电机使用寿命。

通过对转子振型分析知道，样机转子在一定轴承刚度支撑下，考虑单边磁拉力时，转子中心轨迹比不考虑单边磁拉力时中心轨迹大。

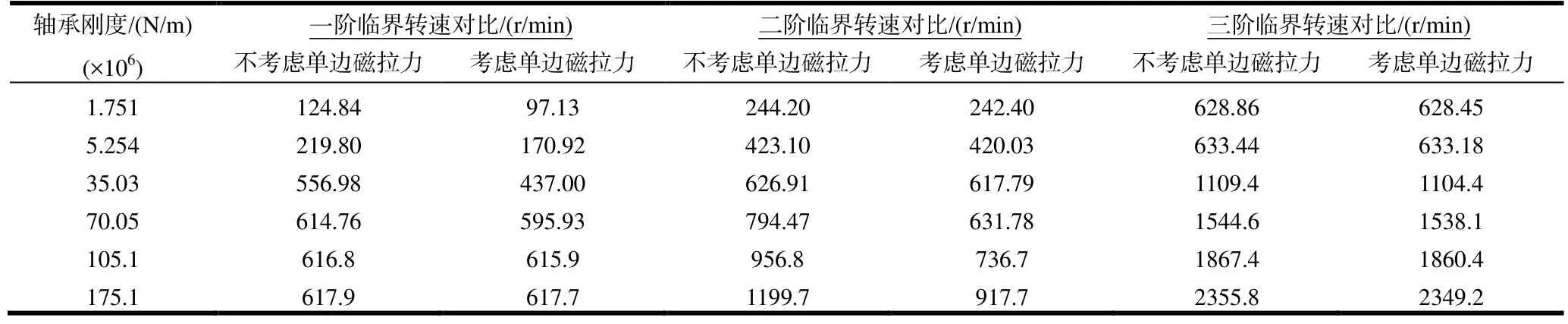
表3 临界转速对比

3 结论

通过对YZYKK1800-20感应电机转子的临界转速及振型计算，分析单边磁拉力对转子—轴承系统振动的影响。得出结论：

（1）样机转子—轴承系统的临界转速与轴承支承刚度密切相关，转子—轴承设计时应综合考虑尽量选取支撑刚度大的轴承。

（2）电机制造与安装时应保证气隙的均匀度。否则，电机内部会产生很大的单边磁拉力，相当于增加铁心段转子的质量，降低了转子—轴承系统的固有频率。

通过对转子—轴承系统临界转速以及振型的计算与分析，为大容量低速感应电机转子动力学分析和设计提供了理论依据。

[1] 郝雪莉. 永磁电动机电磁振动噪声的计算分析研究[D]. 沈阳: 沈阳工业大学, 2010: 15-22．

[2] 徐俊. 临界转速计算及其在电动机转子设计中的应用[D]. 上海: 上海交通大学, 2010: 13-25．

[3] 李建伟, 庞立军, 贾伟, 等. 水轮发电机不平衡磁拉力计算[J]. 上海大中型电机, 2014(2): 29-32．

[4] Daut, I., Maizana, D., Uthman, S., et al. Different clamp stress impact on losses and flux distribution between two of 3 phase distribution transformer 1000 kVA assembled with stagger yoke of transformer core lamination[J]. IEEE Intelligent and Advanced Systems, 2007(4): 851-853．

[5] Ye Liu, Zhuoran Zhang, Ji Dai. Feature investigation of axial flux leakage of a hybrid excitation synchronous machine [J]. IEEE Electrical Machines and Systems, 2014(3): 1971-1976．

[6] RASMUSSIN K F, DAMES J H. Analytical and numerical computation of air-gap magnetic fields in brushless motors with surface permanent magnets[J]. Industry Applications IEEE Transactions on Magnetics, 2000 (6): 1547-1554．

[7] 魏曙光, 马晓军, 闫之峰, 等. 基于Ansoft的定子双绕组感应发电机设计分析[J]. 微特电机, 2013, 41(1): 1-3, 10.

[8] 唐华瑜. 感应电动机电磁场有限元计算[J]. 内江科技, 2013(4): 69．

[9] 袁惠群. 转子动力学基础[M]. 北京: 冶金工业出版社, 2014: 236-237．

[10] 郑劲, 丁雪兴, 贾汝民, 等. 基于传递矩阵法的干气密封试验台转子固有频率计算[J]. 化工机械, 2013, 40 (S): 184-187．

[11] 单丽, 盛海军, 鲍晓华. 单边磁拉力对湿式潜水电机转子振动的影响[J]. 电机技术, 2013(4), 25-28．

[12] 徐爱杰． 高速电机转子系统动力学特性分析[D].哈尔滨: 哈尔滨工业大学, 2012: 15-30．

孟大伟（1956-），1999年毕业于哈尔滨工业大学电机与电器学科，获工学博士学位，长期从事电机与电器专业教学与科研以及教学管理工作，博士生导师。

审稿人：孙玉田

Analysis of Effect of Unbalanced Magnetic Pull on Rotor Critical Speed of Large Asynchronous Motor

MENG Dawei, SHI Daolong, YU Xiwei, LIU Huimin
(College of Electrical & Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China)

Taking the 11kV-20p-6500kW large-scale three-phase asynchronous motor as an example, the influence of unbalanced magnetic pull on the vibration of rotor is analyzed. The method FEM is used to calculate the unbalanced magnetic pull of rotor. The dynamic model of rotor in this large-scale three-phase asynchronous motor is established using the software of ARMD. The first three orders of nature frequency of rotor are obtained with the boundary condition of whether the unbalanced magnetic pull is applied in model or not. Through the compare and analysis of the calculation results, the unbalanced magnetic pull is proved to reduce natural frequency of rotor, and the increase of stiffness of bearing support is beneficial to eliminate this impact. The results of this paper provide the theoretical foundation for the mechanical design of shaft of the large-scale three-phase asynchronous motor, and then improve the working performance.

FEM; unbalanced magnetic pull; ARMD; rotor dynamics; natural frequency

TM346

A

1000-3983(2015)06-0015-05

2014-08-17