磁流变阻尼器对大跨斜拉桥的脉动风振控制研究

徐 萌，贾大焕，徐赵东，，罗月静

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096；2.中国核电工程有限公司郑州分公司，河南 郑州 450000；3.广西交通科学研究院，广西 南宁 530007)

磁流变阻尼器对大跨斜拉桥的脉动风振控制研究

徐 萌1，贾大焕2，徐赵东1，3，罗月静3

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 210096；2.中国核电工程有限公司郑州分公司，河南 郑州 450000；3.广西交通科学研究院，广西 南宁 530007)

斜拉桥属于柔性桥梁，易在风振激励下产生大幅振动，利用磁流变阻尼器实时根据风振响应对斜拉桥进行智能减振是一个国际性的前沿热点研究课题。文章针对此课题对一加有磁流变阻尼器的斜拉桥建立了平面杆系有限元模型，基于模拟的三维脉动风场，计算出脉动风场下斜拉桥的风振响应，并根据风振响应通过LQR三态控制策略实时确定磁流变阻尼器的控制电流和输出力。研究表明：加设于箱梁和主塔之间的磁流变阻尼器可有效减小斜拉桥箱梁的风振响应。

斜拉桥；风振控制；磁流变阻尼器；动力响应

0 引言

现代斜拉桥自20世纪70年代进入中国以来发展迅速，已成为大跨度桥梁的

最主要桥型。斜拉桥是由主塔、主梁、斜拉索三种基本构件组成的桥跨结构支承在桥墩上的索体承重结构，但斜拉桥柔度大、阻尼小，易在风振激励下产生大幅振动。这种大幅振动不仅给行人、司机心理上带来不适，而且还将引起桥梁结构的疲劳，甚至危及结构的安全，影响桥梁的正常使用[1]。因此斜拉桥的脉动风致振动控制已成为必须解决的关键问题之一，国内外学者对斜拉桥的风致振动控制问题进行了相关研究。Pintoda等[2]由Hamilton原理导出了斜拉索在竖向激励下的非线性振动方程，研究了不同倾斜角的索产生参数振动时的振幅及拉索的内力；湖南大学陈政清教授[3]在湖南岳阳洞庭湖大桥上建立了风雨振观测系统；同济大学顾明教授[4]等在试验的基础上对拉索风雨振机理进行了研究。2002年，磁流变阻尼器首次应用于岳阳洞庭湖大桥成功地控制拉索风雨激振，此后磁流变阻尼器对斜拉桥的减振得到了广泛应用。

1 大跨斜拉桥有限元建模

1.1 斜拉桥平面杆系模型

本文斜拉桥模型的基本假定为：桥塔与桥墩为固结；主梁与桥塔连接处为竖向、转角自由度耦合，顺桥向自由度释放(即纵飘体系)；主梁两端支承为竖向铰支承；斜拉索两端分别铰结于主梁及桥塔。拉索的最佳倾斜角为45°，本文中的斜拉桥拉索倾斜角范围为[26.5° 72°]，与合理变化范围25°～65°较为符合。斜拉桥模型的结构基本参数如表 1所示，模型如图 1所示。

表1 斜拉桥结构基本参数值表

图1 斜拉桥结构布置及风速模拟点位示意图(单位：m)

平面杆系斜拉桥有限元建模过程应遵循以下原则：斜拉桥桥塔、桥墩均可采用平面梁单元；斜拉索采用考虑垂度影响的平面杆单元(弹性模量为考虑材料变形、构造伸长和垂度变化的等效弹性模量)[5]；斜拉桥的结构阻尼比宜≤3%；非线性分析时，也可采用Rayleigh正交阻尼；桥面系通常有脊梁模式、Ⅱ形模式、双主梁模式和三主梁模式四种[6]，本文的平面杆系模型中依据具体情况采用平面化的脊梁模式。平面杆系斜拉桥结构的有限元建模基本内容和步骤见图2。

质量矩阵有一致质量矩阵与集中质量矩阵两种常用形式，本文梁单元和杆单元均采用一致质量矩阵阻尼。到目前为止，材料阻尼的数学模型有很多，但都有其使用范围和局限性，基于结构阻尼机制的复杂性和实用性考虑，本文采用常用的Rayleigh正交阻尼模型。

图2 平面杆系斜拉桥建模程序框图

2 随机脉动风场模拟

2.1 三维脉动风场

在笛卡尔坐标系下，大跨度斜拉桥的三维风场[7]可表示为：

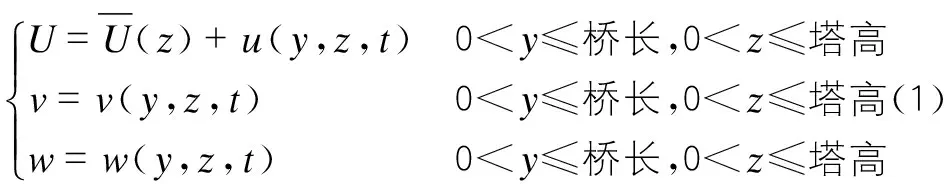
t——时间。

已有研究表明，斜拉索的振动对结构的总体响应影响较小，因此大跨度斜拉桥总体风致响应分析中，可仅考虑桥塔与主梁上的脉动风场。

由于桥塔为竖向线状结构，可以忽略竖向脉动风量w的作用，因此竖向脉动风场可仅考虑主梁分布的各点。主梁为顺桥向线状结构，可忽略顺桥向脉动分量v的作用，仅考虑桥塔上各点的情况。空间相干函数采用Devenport形式[8]，当两点间距>100m且风振频率在大跨斜拉桥卓越振动频率范围内(0.2～2.0Hz)时，风速间的相关性很弱。由于大跨度斜拉桥的桥塔间距(即跨度)一般很大，因此可忽略桥塔间风速的相关性，将其分别作为独立的随机过程。桥塔上各点和主梁跨中附近各点相距较远，横桥向脉动风速的相关性较弱；塔梁结合处附近各点风速的相关性较强，但该处的风致振动通常较小，风对其的广义作用力仍较小；此外，由于桥塔(独柱式除外)横桥刚度一般较大，由顺桥向脉动风引起的桥塔的横桥向振动较小，其与主梁振动的耦合性亦较弱，因此，对于横桥向脉动风场可忽略桥塔和主梁间风速的相关性，分别将其作为独立的风场进行模拟。

综上所述，根据大跨度斜拉桥结构形式及振动型态的特点，结合自然风的相关特性，可将斜拉桥面状三维相关的随机风场简化为桥塔分别沿x、y方向及主梁分别沿x、y方向的多个独立的线状一维风速场。

脉动风荷载的计算机模拟方法主要有两类：基于一系列三角函数加权叠加的谐波合成法(WAWS法)[9]和采用自回归模型的线性滤波器法(AR法)。本文的随机脉动风荷载采用谐波合成法模拟得出。

2.2 风速时程模拟

平面杆系斜拉桥跨度组合为50m+125m+50m=225m，主塔高30m。其风场可简化为3个独立的一维多变量随机风速场，如表2所示，沿主梁从左到右等间距(10m)分布了23个模拟点，主塔从下向上等间距(5m)分布了5个模拟点，模拟点如图1所示。

表2 斜拉桥一维风速场位置图

MATLAB风场模拟B程序中的主要参数如下：跨度L=225m；主梁离地有效高度z=20m；地面粗糙度z0=0.03m，主梁处平均风速U(z)=30.0m/s；模拟点数n=23；模拟点间距Δ=10m；上限截至频率ωup=2π rad/s；频率等分数N=256；模拟采样时距Δt=0.5s；目标谱采用Kaimal水平脉动风速谱[7]。

模拟得到的第1点的风速时程的片段图见图3。

图3 第1点风速模拟时程图

3 磁流变阻尼器——斜拉桥风振控制

3.1 未控状态下斜拉桥风振响应

未控状态下，系统状态空间表达式为Z(t)=AZ(t)+DW(t)，在MATLAB中采用lsim函数[10]进行仿真分析。本文将MATLAB程序与ANSYS程序进行对比以验证MATLAB程序的正确性。风荷载时程激励下MATLAB和ANSYS两种软件程序得出的斜拉桥跨中结点竖向位移对比图见图4，其误差在5%以内，表明了MATLAB程序的正确性和可行性。

3.2 磁流变阻尼器减振系统的控制策略

本文分别采用线性二次型(LQR)经典最优控制和三态控制策略对设有磁流变阻尼器的大跨斜拉桥中脉动风致振动控制进行研究分析。

通过线性二次型(LQR)经典最优控制算法可得出磁流变阻尼器控制系统的最优控制力U*(t)，通过调节磁流变阻尼器的主要参数(电流)使其所产生的阻尼力向最优控制力逼近，从而获得较为理想的控制效果。

式中：Fdmin、Fdmax——分别为电流I=OA和I=Imax时磁流变阻尼器的阻尼力；

xi——被控结点处的位移；

α——阻尼器加设角度，见图 5。

运用LQR三态控制策略需根据LQR算法得出最优控制力，改变阻尼器的控制参数，即输入电流(I=OA、I*和Imax)的大小，控制过程中阻尼器的电流参数随斜拉桥的风振响应实时改变，充分地利用了磁流变阻尼器的连续可调性和快速出力能力。LQR三态控制策略较被动控制效果明显，不会引起受控结构的动力反应局部放大及阻尼器阻尼力超调现象。LQR三态控制策略示意图见图6。

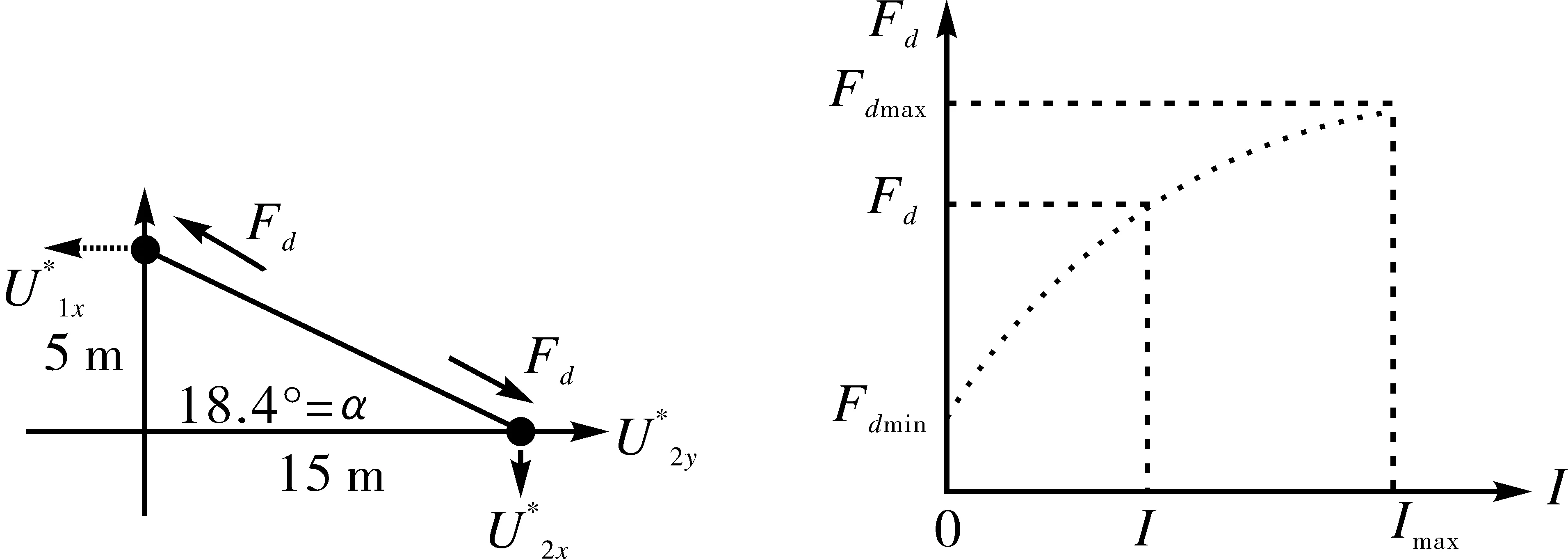
图5 阻尼器安装及电流调节示意图

图6 LQR三态控制策略简图

3.3 斜拉桥受控状态下风振响应结果

根据磁流变阻尼器宜放置在受控结构位移最大处的原则，在斜拉桥塔梁连接处按一定角度对称地安装磁流变阻尼器，阻尼器选用剪切阀式磁流变阻尼器。依照LQR算法得出的最优阻尼力设定阻尼器个数N及最大出力Fdmax，本文采用的阻尼器的个数N=2、最大出力Fdmax=200kN，又由于低角度放置阻尼器能够起到控制桥面主梁纵飘位移的同时降低主梁跨中竖向位移的效果，因此将阻尼器加设角度设置为α=18.4°。

未控、LQR控制和LQR三态控制条件下斜拉桥的纵飘位移以及加速度响应图见图7。

图7 主梁纵飘动力响应图

斜拉桥主梁各点的纵飘位移相近，主梁上任一结点的顺桥向位移控制可以视为斜拉桥主梁纵飘位移的整体控制。由图7(a)可以看出，斜拉桥纵飘位移在无控状态下为14.15cm，LQR最优控制下为4.69cm，减幅66.85%，LQR三态控制下为7.10cm，减幅49.82%。由图7(b)可以看出，斜拉桥纵飘加速度峰值在未控状态下为1.28m/s2，LQR最优算法控制下为0.42m/s2，减幅67.18%，LQR三态控制下为0.62m/s2，减幅51.56%。LQR三态控制效果虽不及LQR最优控制，但纵飘位移以及加速度均得到了有效的控制，表明磁流变阻尼器对大跨斜拉桥纵飘位移、加速度响应控制效果良好。

由于阻尼器加设的角度稍低，在控制桥面纵飘位移同时，也提供了竖向的阻尼力，对斜拉桥主梁跨中竖向位移也有一定的控制作用。主梁跨中结点1竖向位移、加速度动力响应图见图8。

从图8(a)可以看出，斜拉桥主梁跨中结点1竖向位移响应峰值在未控状态下为8.85cm，LQR最优控制下为8.07cm，降幅8.8%，LQR三态控制策略下为5.95cm，降幅32.77%；从图8(b)中可以看出，竖向加速度峰值未控状态下为0.80m/s2，LQR最优控制下为0.62m/s2，降幅22.5%，LQR三态控制策略下为0.46m/s2，降幅42.5%。分析结果表明磁流变阻尼器对大跨斜拉桥竖向位移、加速度控制效果良好。

图8 主梁跨中竖向风振动力响应图(结点1)

4 结语

本文基于MATLAB软件编写了大跨斜拉桥平面杆系有限元模型，采用谐波合成法模拟随机脉动风荷载，计算得出斜拉桥在脉动风场下的风振响应。并将MATLAB软件程序计算结果与ANSYS计算结果进行对比，结果表明MATLAB软件程序的正确性和可行性。

根据得到的风振响应通过LQR经典最优控制以及LQR三态控制策略实时确定磁流变阻尼器的控制电流和输出力，从而对设有磁流变阻尼器的大跨斜拉桥的脉动风致振动控制进行研究分析。分析结果表明在斜拉桥箱梁和主塔之间加设磁流变阻尼器可有效减小斜拉桥箱梁的风振响应。

[1]Abdel-GhaffarAM,KhalifaMA.Importanceofcablevibrationindynamicsofcable-stayedbridges[J].JournalofEngineeringMechanics, 1991, 117(11): 2571-2589.

[2]CostaAP,MartinsJAC,BrancoF,etal.Oscillationsofbridgestaycablesinducedbyperiodicmotionsofdeckand/ortowers[J].JournalofEngineeringMechanics, 1996, 122(7): 613-622.

[3]王修勇,陈政清,高赞明, 等.磁流变阻尼器对斜拉索振动控制研究[J]. 工程力学, 2002, 19(6): 22-28.

[4]GuM,DuX.Experimentalinvestigationofrain-wind-inducedvibrationofcablesincable-stayedbridgesanditsmitigation[J].JournalofWindEngineeringandIndustrialAerodynamics, 2005, 93(1): 79-95.

[5]贺拴海.桥梁结构理论与计算方法[M]. 北京: 人民交通出版社, 2003.

[6]蔺鹏臻, 刘世忠.桥梁结构有限元分析[M]. 北京: 科学出版社, 2008.

[7]陈政清.桥梁风工程[M]. 北京: 人民交通出版社, 2005.

[8]曹映泓,项海帆,周 颖.大跨度桥梁随机风场的模拟[J]. 土木工程学报, 1998， 31(3): 73-79.

[9]罗俊杰,韩大建.大跨度结构随机脉动风场的快速模拟方法[J]. 工程力学, 2008， 25(3): 96-101.

[10]徐 斌,高跃飞,余 龙.MATLAB有限元结构动力学分析与工程应用[M]. 北京: 清华大学出版社, 2009.

Study on the Fluctuating Wind-induced Vibration Control of Magnetorheological Damper for Large-span Cable-stayed Bridges

XU Meng1，JIA Da-huan2，XU Zhao-dong1,3，LUO Yue-jing3

(1.Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education，Southeast University，Nanjing，Jiangsu，210096；2.Zhengzhou Branch of China Nuclear Power Engineering Co.，Ltd.，Zhengzhou，Henan，450000；3.Guangxi Transportation Research Institute，Nanning，Guangxi，530007)

Cable-stayed bridge belongs to the flexible bridges，which is easy to produce the substan-tial vibration under wind excitation，thus the intelligent vibration damping for cable-stayed bridges according to real-time wind vibration response by using the magneto-rheological dampers is a fore-front hot research topic internationally.Aiming at this topic，this article estab-lished the plane frame fi-nite element model on a cable-stayed bridge with magneto-rheological dampers，and based on threedimensional simulated fluctuating wind field，it calculated the wind-induced response of cable-stayed bridge under fluctuating wind field，and according to wind-induced response，it determined the realtime control current and output force of MR damper through LQR tri-state control strategy.Studies have shown that：MR damper installed between box girders and main tower can effectively reduce the wind-induced vibration response of cable-stayed bridges.

Cable-stayed bridge；Wind vibration control；MR damper；Dynamic response

徐赵东，教授，博士生导师，国家中青年科技创新领军人才，教育部新世纪优秀人才，江苏省333高层次人才，江苏省创新人才学术带头人，东南大学特聘教授。主要从事结构抗震与振动控制、结构健康监测、智能材料与结构等方面的研究。主持完成863计划、国家自然科学基金重大研究计划、支撑计划重点课题、973专题、4项国家自然科学基金等。在ASCE等国内外核心刊物上发表论文148篇，其中SCI收录46篇，EI收录93篇，出版专著3部。获国家发明专利11项、实用新型专利13项。获国家技术发明二等奖 (排名第一)、江苏省科学技术一等奖 (排名第一)、中国建筑材料科学技术发明一等奖 (排名第一)、江苏省科技进步二等奖 (排名第一)、江苏省科技进步一等奖(排名第四)、中国振动工程学会青年科技奖、江苏省青年科技奖等二十余项。

U448.27

A

10.13282/j.cnki.wccst.2015.06.010

1673-4874(2015)06-0039-05

2014-05-06

专家信息EXPERTS

徐 萌，硕士研究生，主要从事磁流变阻尼器对斜拉桥的风致振动控制研究工作。

广西省特聘专家资助计划；国家中青年科技创新领军人才支持计划