基于改进蚁群算法的城市交通最短路径算法
2015-07-01张水舰
张水舰
(湖州职业技术学院,浙江 湖州 313000)
基于改进蚁群算法的城市交通最短路径算法
张水舰
(湖州职业技术学院,浙江 湖州 313000)
蚁群算法作为一种寻优性能良好的智能算法,是解决最短路径问题的一种有效的方式。但是,基本蚁群算法真接运用于交通网络中路径的寻优存在一些不足。文章针对基本蚁群算法的不足对其进行了改进,根据交通网络的特点限定了解的搜索范围和改进了蚁群算法的转移规则,并对信息素的更新规则作了改进。仿真实验结果表明,改进了的蚁群算法在求解最短路径时比基本蚁群算法性能有较大的提高。
城市交通;蚁群算法;最短路径;交通网络
0 引言
随着城市交通量的急剧增加,交通拥堵问题日益严重,已经影响到了人们的出行,找到一条最短的出行路径是出行者首先想要做的事情。最短路径问题已成为众多学者研究的一个热点问题,此问题的解决可以为交通流分配、城市道路设计等交通网络优化提供理论基础。可以说最短路径问题是关系到城市
发展的一个重要问题,具有重要的理论和实践意义。国内外学者对在交通网络中寻求最短路径的算法进行了大量的研究,并取得了丰硕的成果。最有代表性就是Dijkstra算法,Dijkstra算法能找到全局最优解[1];为了提高算法的效率,许多研究者也提出了一些启发式算法,如A*、遗传算法、免疫算法等。最短路径的选择,最后都归结为找到一条耗费成本最少的路径,如时间最快、距离最短等。通过最短路径的选择,可以将无序的交通出行变得有序,减少出行的盲目性,以优化交通流的分布,提高城市交通网络的效率,缓解交通拥堵。智能优化算法的兴起为在复杂交通网络中寻找最短路径提供了可行的方式。意大利学者Colorni A,Dorigo M和Maniezzo V于1992年提出了一种新型的智能优化算法——蚁群算法(Ant Colony Optimization,ACO),实践证明蚁群算法具有良好的寻优性能[2-4]。该算法模拟蚁群搜寻食物的过程中按最短路径运送食物的能力,这种找到最短路径的能力跟在交通网络中找到最短出行路径是同一性质的优化问题,因此蚁群算法可以用在交通网络最短路径的寻找上。
1 最短路径诱导蚁群算法
城市交通网络是具有空间分布的地理网络,具有路线长度、通行时间、路况等属性。城市交通网络是由交叉路口抽象成的节点和由路线抽象成的边组成的网络,并把交通阻抗表示为网络边的权值,因此城市交通网络是一个加权的有向图。交通网络可以映射成一个连通带权有向图G:(V,E,W)。其中,V表示网络上所有节点的集合,E表示网络上所有边的集合,W是网络边的非负权值。
1.1 基本蚁群算法
昆虫学家在研究蚂蚁时发现蚂蚁在觅食过程中会释放一种特有的物质——信息素,蚂蚁在寻找路径的过程中能检测到其它蚂蚁所释放的信息素,并利用信息素来引导自己的移动方向,且以较高的概率选择信息素量较多的路径,蚂蚁在此路径上行进时又释放出信息素,因此信息素量多的路径经过的蚂蚁会更多,经过的蚂蚁越多又会增加此路径上的信息素量,由此大量蚂蚁的觅食过程就构成一种对信息素的正反馈过程,从而逐渐找到一条最短的觅食路径。蚁群算法就是模拟蚂蚁觅食过程中形成最短路径的原理,设计出的一种群智能算法[5-6]。
如图1所示,蚂蚁从蚁穴出发去寻找食物,在最初阶段由于两条路径上都没有信息素,蚂蚁以相同的概率选择这两条路径,然而走短路径的蚂蚁会更快地回来,经过路径的次数也更多,留下信息素自然就多,经过一段时间后,在短路径上会有更多的信息素,诱使蚂蚁选择短路径。
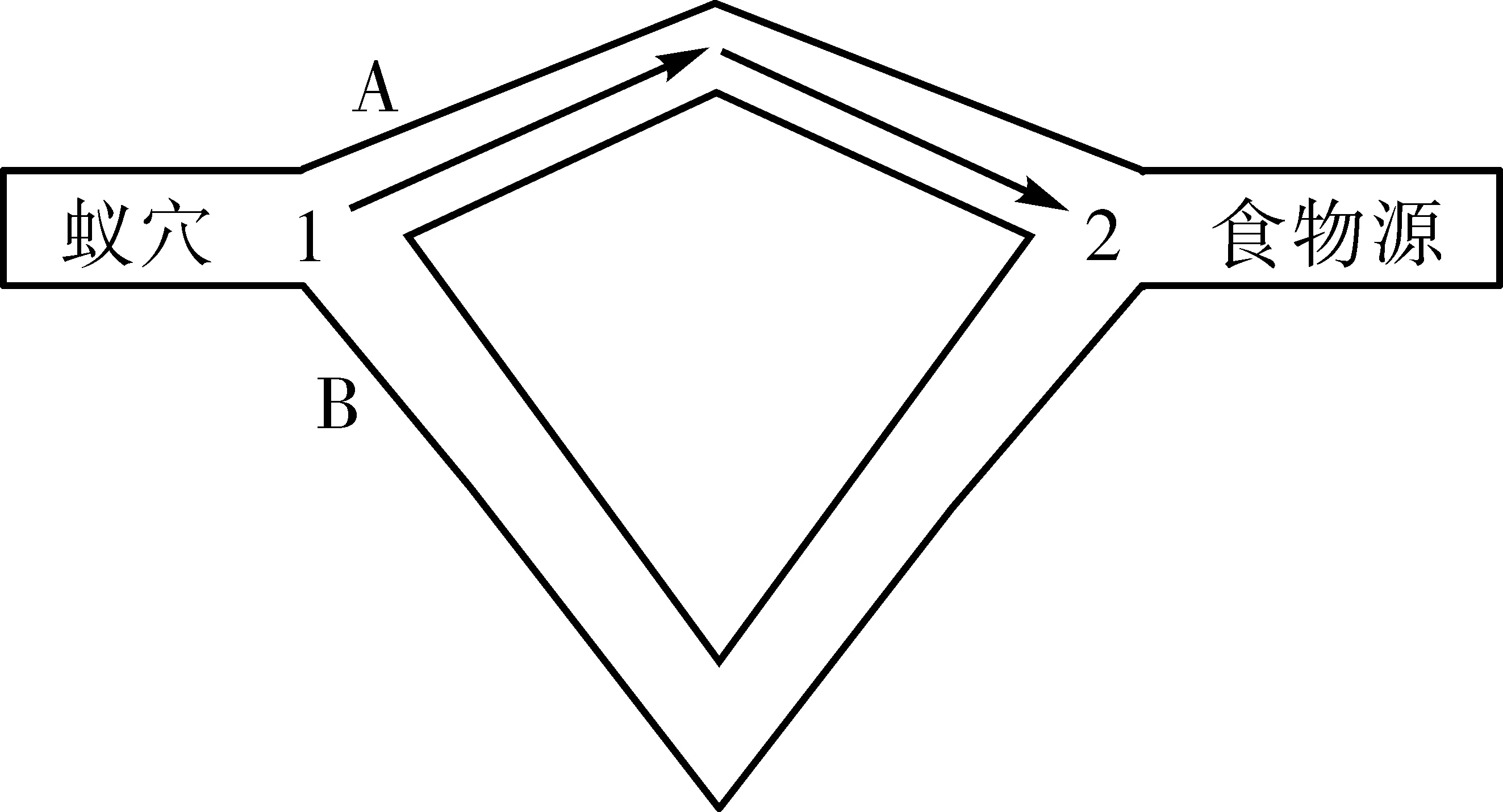
图1 蚂蚁觅食所选路径示意图
基本蚁群算法的流程如下:
(1)蚁群A(t)初始化:确定蚁群规模等;
(2)根据蚂蚁到达目的地的路径长度计算每只蚂蚁的适应度;
(3)根据蚂蚁的适应度,对蚂蚁所经过的路径按一定的规则释放信息素;
(4)后面出发的蚂蚁根据前面蚂蚁在路径上所留下的信息素浓度选择到达目的地的路径;
(5)留在路径上的信息素随着时间按一定速率不断消散。
蚁群初始化使各条路径上的信息素浓度相等,即当t=0时,τij(0)=C(C为常数),τij(0)表示初始时刻路段ij的信息素量。每只蚂蚁k=(k=1,2,…,m)(设蚂蚁的规模为m)在觅食过程中根据路径上的信息素浓度按照随机比例规则选择下一行进路径,即在t时刻处于位置i的蚂蚁k按一定概率选择移动到位置,此概率称为转移概率,按公式(1)计算:
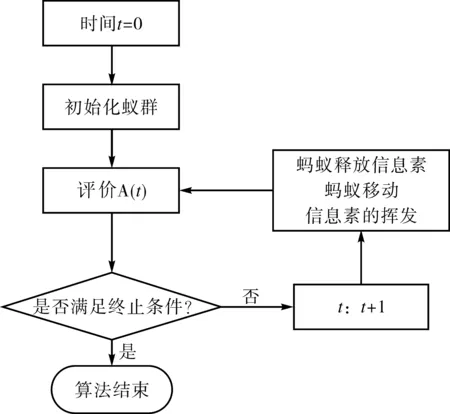
图2 基本蚁群算法流程图
(1)

notcrossedk——蚂蚁k从位置i下一步允许移动到的位置,notcrossedk={0,1,…,n-1}。
在所有蚂蚁完成一次路径的寻找后,各路段上信息素量按下式进行更新:
τij(t+1)=ρ·τij(t)+Δτij(t,t+1)
(2)
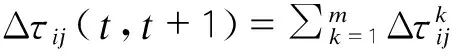
(3)
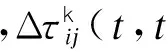
1.2 改进的最短路径蚁群算法
如上所述蚁群算法是模拟蚂蚁觅食过程中寻到最优路径的原理。实践证明蚁群算法具有较强的寻优能力。虽然蚁群算法在许多优化问题中表现出优良的性能,然而还得对基本蚁群算法进行改进才能适用某些特定领域的优化问题。例如,当蚁群算法运用于在交通网络中求解最短路径时,会出现不适应的问题:(1)基本蚁群算法中蚂蚁的行进过程中选择下一位置是遵循随机原则,没有对觅食方向进行引导,影响了搜索的速度;(2)由于信息素容易在局部最优解附近增加过大,造成寻优结果易于陷入局部最优解。
本文充分利用基本蚁群算法的优良性能,结合交通网络最短路径问题自身的特点,对基本蚁群算法进行了改进,提出了一种适合求解交通网络最短路径问题的蚁群算法。针对基本蚁群算法的不足之处,对基本蚁群算法作了如下改进:
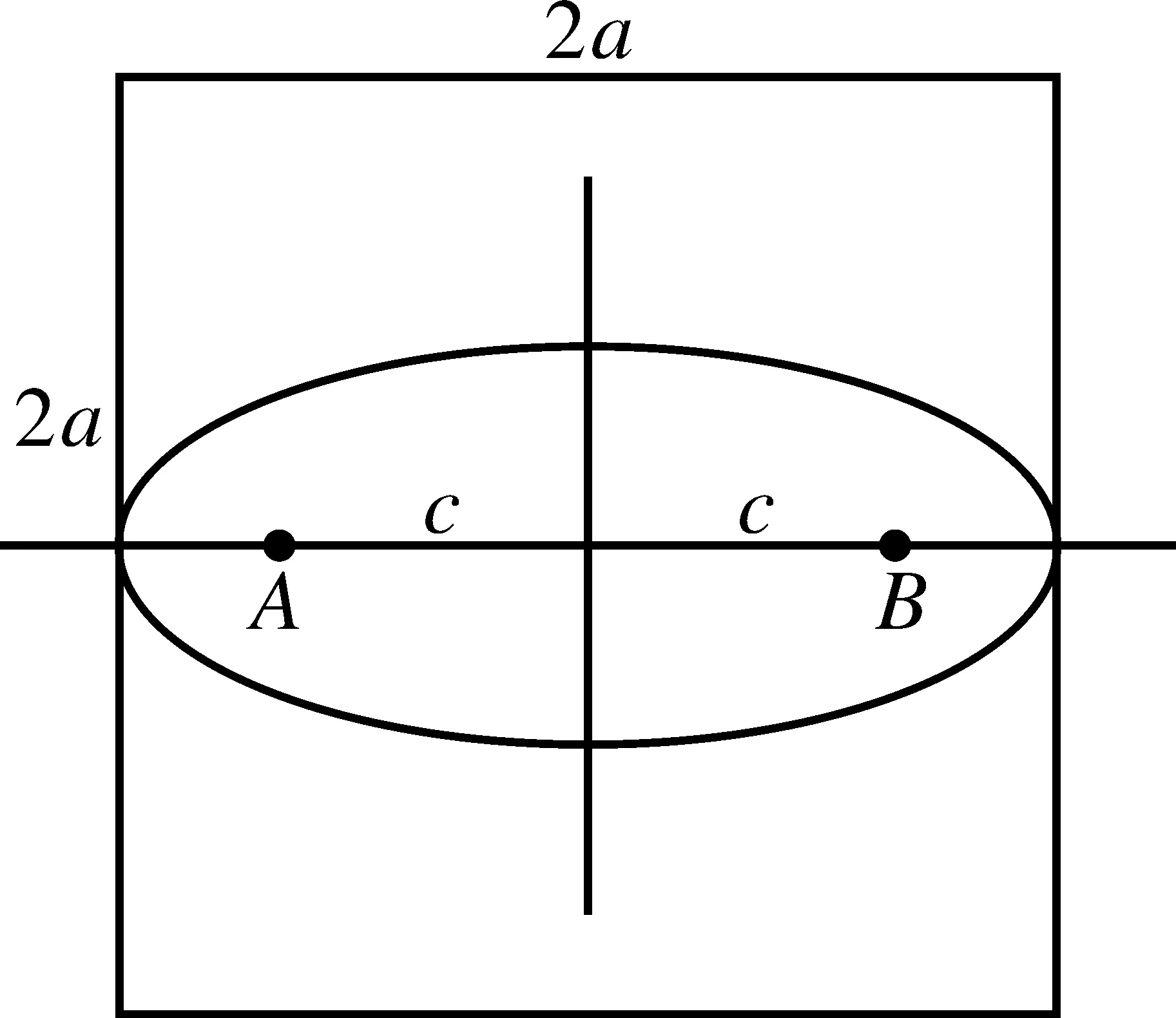
图3 蚂蚁搜索范围示意图
(1)具有地理分布的城市交通网络,相隔较远的两点之间一般不会有直接连接两点的直通路径,但两点之间的最短路径一般是沿着这两点之间的连线分布的,不会偏离这条直线很远的距离,为此可以限定搜索范围,这是符合实际情况的,在实践中是合理的。为此在算法的实现过程中可以将蚂蚁的搜索行为集中到一定范围内,即限制在最优解的附近,这可以提高搜索效率,加快收敛速度,提高解的质量。
搜索范围按如下方法确定,如图3所示,假设点A和B是起讫点,以A和B点作为椭圆的焦点,以AB连线的直线距离作为椭圆的焦距2C。搜索范围取图中的椭圆,椭圆的面积取为以长轴2a为边长的正方形的面积的三分之一,由此可以得到下式:
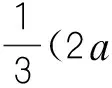
(4)
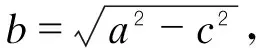
(5)
由(5)式可解得:
(6)
由此可以确定出椭圆的大小。
(2)为解决搜索的方向性问题,需改进蚁群算法的转移规则。如上分析可知,在交通网络中从起始点出发到终点的最短路径不会偏离起始点与终点的连线很远的距离,为此可用当前节点和下一节点的连线与当前点和终点的连线的交角来表示方向,这个夹角的取值在0~π之间。如图4所示,假设A点为起点,B点为终点,某只蚂蚁已从A点行进到了节点i,在选择下一个节点时假设有两个节点j和E可选择,从图上可以看出ij与CB的夹角θ小于iE与iB的夹角φ,这时可以看出ij自然更偏向于i跟B的连线。如果路段ij和iE上信息素量相等、路况大致相同,蚂蚁将沿着路段iE行进,这也是符合平常人们选择路径的心理的。为此可对蚂蚁的转移规则进行改进。
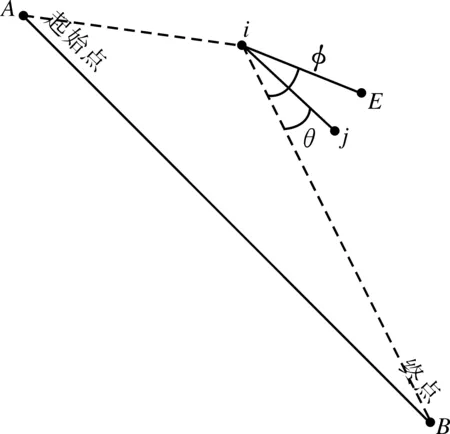
图4 搜寻方向示意图
在改进的最短路径蚁群算法中,在计算蚂蚁在行进过程中选择下一位置的转移概率时,对式(1)中的系数ηij进行了改进,加入了方向的启发信息。ηij按下式计算:
ηij=1/wij·θ
(7)
其中wij为路段ij的交通阻抗,θ如上所述。从式(7)中可以看出,当路段的阻抗越小,路段越朝向终点时ηij的值就越大,此路段被选择的概率也就越大。
(3)对信息素更新规则的改进
在一次循环之后,基本蚁群法要取每只蚂蚁经过的路径进行信息素的更新,这种信息素更新规则可以防止算法的寻优解陷入局部最优解,但会减慢收敛速度。为了提高搜索质量,改进算法的性能,引进遗传算法中的选择机制,对基本蚁群算法的信息素更新规则进行改进。首先选出适应度的蚂蚁,即选出前m只所经路径最短的蚂蚁,然后再对选出的蚂蚁所经过的路径进行信息素的更新,信息素的释放量也根据路径的长短依次递减。信息量的增量仍然按公式(2)、(3)计算,此时m表示所经路径为最短的前m只蚂蚁。为避免搜索的停滞,规定交通网络上的每条边的信息素量的值限制在[τmin,τmax],某条边的信息量大于τmax时按τmax计算,当信息素小于τmin时,按τmin计算。
2 仿真试验
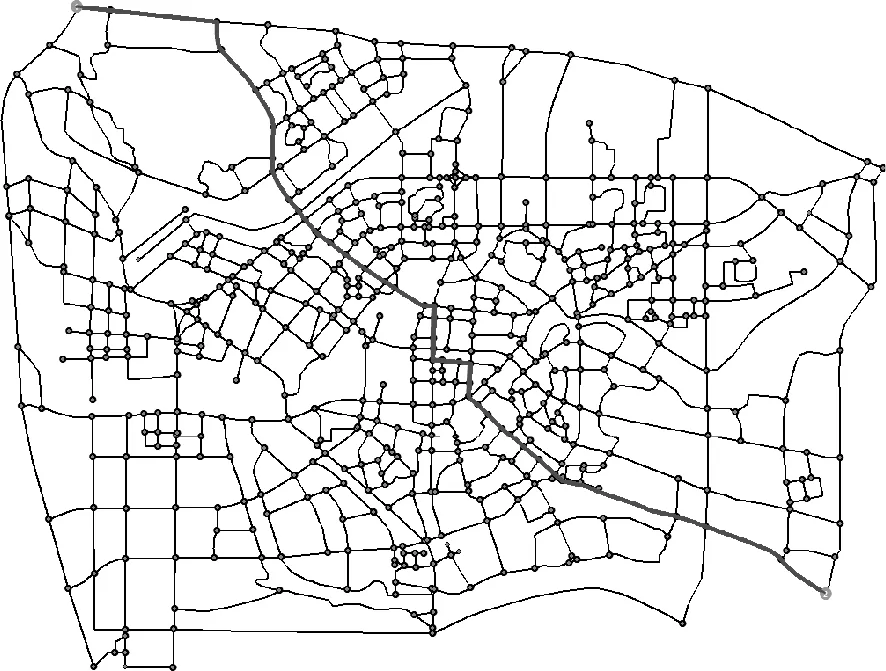
图5 某城市交通网络图
对以上所述最短路径蚁群算法进行试验,以1015个节点,1006条路段的交通网络作为试验对象(图5),在ArcGIS10.2的环境下,以C#作为开发工具仿真试验了改进蚁群算法。选取了三组起讫点做试验,试验结果如表1所示(解为到达目的地的最短时间)。从结果中可以看出改进了的蚁群算法比基本蚁群算法性能有明显的提高。
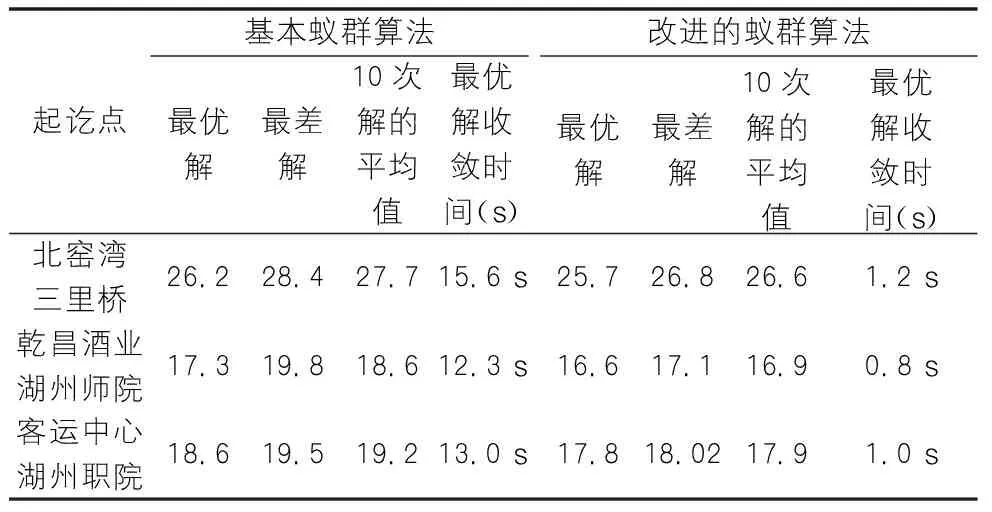
表1 试验结果表(单位:min)
3 结语
蚁群算法是性能优良的智能优化算法,本文对基本蚁群算法进行了改进,使蚁群算法适合在交通网络上进行路径寻优。本文在充分利用基本蚁群算法良好的寻优性能的基础上,根据交通网络地理空间分布特征,以及起讫点之间最短线路的方向性,对算法的搜索范围和信息素更新规则等作了改进。
试验表明,与直接运用基本蚁群算法求解最短路径相比,改进的最短路径蚁群算法能够有效地找到起讫点之间的最短路径。本文提出的最短路径蚁群算法可用于人们出行中寻求最短的出行路径,也可用于交通流的分配中,具有一定的理论和现实意义。
[1]郝新刚,任传祥,刘法胜.基于改进Dijkstra算法的路径优化仿真研究[J].西部交通科技,2010.11:19-22.
[2]梁满朝,李文勇,李福祥.基于蚁群算法和群决策理论的动态路径优化研究[J].西部交通科技,2012(2):58-63.
[3]宋锦娟,白艳萍.基于改进蚁群算法的最短路径问题研究及应用[J].数学的实践与认识,2013,43(3):156-164.
[4]马 军,王 岩.改进的蚁群算法求解旅行Agent问题[J].计算机工程与应用,2010,46(11):35-37.
[5]李士勇,陈永强,李 研.蚁群算法及其应用[M].哈尔滨工业大学出版社,2004.
[6]马 良,朱 刚,宁爱兵.蚁群优化算法[M].上海:科学出版社,2008.
Shortest Path Algorithm of Urban Traffic Based on Improved Ant Colony Algorithm
ZHANG Shui-jian
(Huzhou Vocational and Technical College,Huzhou,Zhejiang,313000)
The ant colony algorithm is an intelligent algorithm with good optimization search performance,and is also an effective way to solve the shortest path problem.However,the path optimization search of directly using the basic ant colony algorithm in transport network has some shortcomings.This article improved the inadequacies of basic ant colony algorithm,confined the search scope and im-proved the transfer rules of ant colony algorithm based on the characteristics of transport network,and improved the updating rules of pheromone.Simulation results showed that the improved ant colony al-gorithm has much better performance than the basic ant colony algorithm in terms of solving the shortest path.
Urban traffic;Ant colony algorithm;Shortest path;Transportation network
张水舰(1972—),讲师,研究方向:交通网络优化。
浙江省教育厅自然科学研究计划项目(Y20 1432450);湖州市科技局项目(2014YZ09)。
U412.37
A
10.13282/j.cnki.wccst.2015.11.020
1673-4874(2015)11-0089-06
2015-10-15
