不规则波作用于直立式建筑物的统计分布

骆俊彬，孙昭晨，梁书秀，赵旭东

（1.中交第四航务工程勘察设计院有限公司，广州510230；2.大连理工大学海岸与近海工程国家重点实验室，大连116024）

不规则波作用于直立式建筑物的统计分布

骆俊彬1，孙昭晨2，梁书秀2，赵旭东2

（1.中交第四航务工程勘察设计院有限公司，广州510230；2.大连理工大学海岸与近海工程国家重点实验室，大连116024）

采用物理模型试验探求不规则波作用下的直立建筑物迎浪面的波谷压力概率分布规律。试验表明，直墙前立波和破碎波两种波浪形态作用下，均可采用韦伯分布来描述波压力概率分布，得出了韦伯分布的形状参数与相对基床高度、基床前肩宽和相对波高有关，并拟合给出经验公式。经可靠性检验表明拟合是合理可靠的。

不规则波；直立式建筑物；波谷作用力；压力概率分布

近些年来，为探求波浪作用下直墙建筑物的设计荷载，许多专家学者做了大量的物理模型试验研究，并得出了一些基于实验的经验公式。然而这些研究成果的对象基本上都是波峰作用的情况。实际工程中，例如沉箱结构或板桩结构后方回填陆域，在这种情况下波谷作用力比波峰作用力更危险，结构的抗倾抗滑主要受墙后主动土压力和波谷压力共同作用影响。另外，如今工程设计大都采用基于概率论的可靠度设计方法，对于不规则波波谷作用的随机特性，确定波谷压力的概率分布是可靠度设计的关键问题。因此，为确定直墙建筑物的波谷作用力，有必要先分析波谷压力的统计分布规律。

康海贵等［1］采用PIV技术测试了直立式建筑物前的流场,研究了近破波对直墙建筑物的作用。俞聿修等［2］通过实验室三维波浪物模试验，提出了在斜向和多向不规则波作用下的直立式建筑物上波浪力计算公式。黄培基（1983）［3］研究了不同水深的波压力，根据统计分析得出波压力的分布函数随深度的变化基本不变。李玉成（1997，1999）［4-5］通过试验研究，分析了波峰作用下立波、近破波和远破波波浪力的统计分布，研究表明三种不同波浪形态的波峰压力均符合双参数的韦伯分布。

国外的研究成果包括Cuomo［6］、Bullock等［7］根据物理模型试验，研究了直立式建筑物冲击压力的作用力特征值和分布规律。Rajasekaran等［8］、Martinelli等［9］分别研究了破碎波冲击压力和非破波动水压力作用于直墙上的波压力，并给出了不同的经验公式。Franco（l998）［10］经过研究分析认为非破波波峰作用下的波压力分布服从双参数韦伯分布。Janice（1998）［11］的试验研究表明不规则波近破波和远破波的波压力分布符合韦伯分布，并给出了韦伯概率分布从脉动力转变到冲击力的临界点。上述国内外的研究基本上都是以波峰作用力为研究对象。对于波谷作用力的统计分布规律目前国内外的研究成果很少，需要开展进一步的工作。

本文是由交通部西部交通课题“重力式码头抗滑、抗倾稳定性的可靠度指标设计方法”研究的阶段性成果，目的是通过物理模型试验研究不规则波对直立式建筑物作用，来探求不规则波波谷作用力的统计分布规律，为深入研究直立式建筑物波浪力的可靠度分析提供基础的研究成果。

1 物理模型试验

本文的工作主要是基于物理模型试验的测量结果，试验是在大连理工大学海岸及近海工程国家重点实验室的海洋环境水槽中进行。水槽长50 m，宽3 m，推板处水深1 m，最大工作水深0.7 m。为尽可能减小和消除波浪反射影响，在水槽末端放置消能装置。断面模型安放在水槽的中间位置，距离造波板30 m。在实验水槽纵轴线方向用两块隔板隔开，以减少反射影响，模型置于外侧槽内。模型结构为重力式沉箱结构，材质为有机玻璃，模型内放置铅块使其不被波浪打动。结构尺寸长40 cm，宽40 cm，高30 cm。如下图1所示，图中参数b为基床前肩宽，d1为基床上水深，d为结构物前水深。

实验采用测压传感器测量结构物迎浪面的波压力。压力传感器采用DJ800型多点压力测量系统，测点的采样频率为500 HZ，10个测压传感器等间距布置于模型结构的中部。传感器直径为0.6 cm，测压点之间间距3.3 cm，如图2所示。试验中采样频率取100 Hz,采样间隔0.01 s，采样时间取125个波周期。

试验选取的不规则波波谱为JONSWAP谱。

（1）波浪条件。有效波高H1/3=8，10，12，14 cm；谱峰周期Tp=1.0，1.2，1.4，1.6，1.8 s；

（2）水深条件。建筑物前水深d=30，40，50 cm；基床上水深d1=10，20，30 cm，结构物模型包括高，中，低三个基床范围；

（3）模型结构。基床肩宽b=10、20、30 cm；水槽底坡i=1/50；基床肩坡m=1∶3。

综上所述，本文实验参数范围：HS/d1=0.27～1.4，d1/ d=0.25～1.0，b/L=0.025～0.2。波浪参数如表1所示，试验中每组重复3次。

试验中，通过布置于模型立面上的10个点压力传感器，测量各测点各试验组次的压强值，仪器自动记录相应的压强历时曲线。每组重复试验三次，本文中的数据取值为三次试验数据的平均值。

为使结构物宽度不影响试验结果，取每一瞬时各测点的波压强和各测点对应的作用单宽面积积分。考虑到试验数据的稳定性要求，按照单位宽度波浪总力从大到小排列的前三分之一大值的平均值P1/3作为统计分析的特征值。

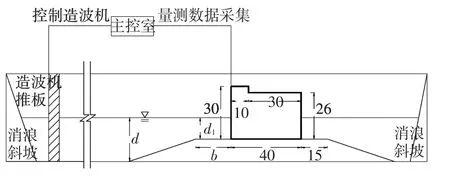
图1 波浪水槽布置图(单位：cm)Fig.1Sketch of experimental setup

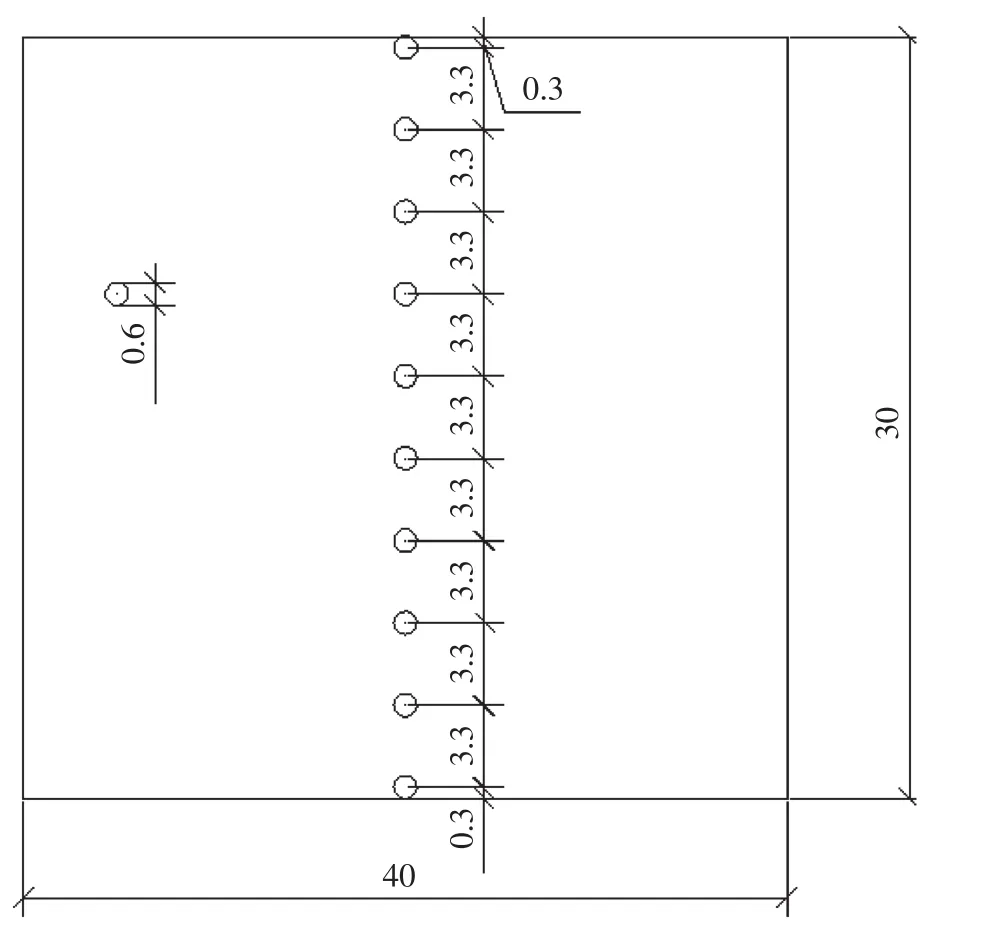
图2 结构物模型顶面点压力传感器布置示意图(单位：cm)Fig.2Sketch of pressure transducers on the top surface of the structure model

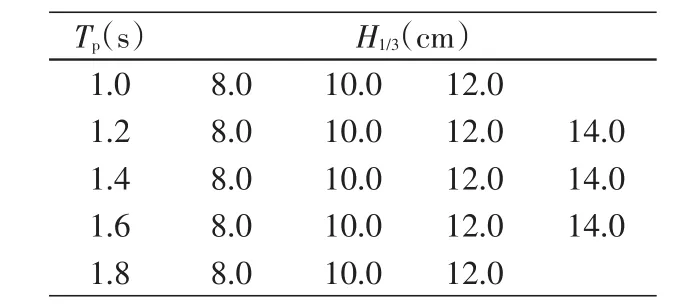
表1 波浪参数Tab.1Wave parameters in experiment

2 波谷压力统计分布

当考虑水深影响时，李玉成［12］认为深水波高的分布符合瑞利分布，浅水波高符合格鲁霍夫斯基分布。若为立波情况，则波浪力的分布服从波高分布。若为非线性破碎波时，波浪力可以采用双参数韦伯分布来描述。然而，波谷作用力分布是否和波峰作用力分布一致，仍需要进行试验研究。

2.1 韦伯三参数分布模型

近年来工程中统计分布采用最多的一种模型是三参数的韦伯分布［13-15］，其概率密度函数为

式中：β＞0，为形状参数；η＞0，为尺寸参数；γ为位置参数，可取γ=0，所以为得到累计分布函数需求出参数β和η。

其累积分布函数为

η值可以取下式的理论值

式中：Γ为伽玛函数。用韦伯分布拟合波浪力分布的优点在于可以和波高分布相关联，该分布的关键因子决定于形状参数β的变化。

2.2 韦伯分布函数参数的估计

韦伯分布因具有广泛的适应性而被众多学者广泛采用。试验得到实测的随机波浪力数据，假定该波浪力分布类型，则可根据相关系数优化法对其参数进行估计。

相关系数优化法是一种常用且非常有效的参数估计方法。基本思想是假设目标函数线性相关，以便确定位置参数，之后用线性回归分析拟合得到形状参数和尺度参数，分析过程如下

对累积分布函数（2）式进行变换，两边取对数得

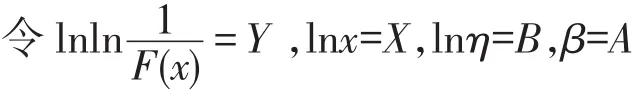
可得

（易产生歧义）由于变量X和Y为线性关系，可根据已知的一组试验数据（xi,F（xi）），通过式（5），变换得到新的数据（Xi,Yi），再经过线性回归分析得出未知参数A、B的值。按这种方法即可由回归方程式求得各波谱系列的直墙波谷压力相对值FH/Fˉ韦伯分布的形状参数β，尺度参数η可根据理论关系式（3）求得。下文就两种波况下，破碎波和立波波谷压力值进行分析。

2.2.1 破碎波波谷压力FH/Fˉ的参数估计

根据破碎波的试验资料，可以分别求得不同基床上水深d1各波谱系列破碎波波谷压力的韦伯形状参数β，尺度参数η可由（3）式求得。结果表明拟合的β值在0.25～0.93间变化。拟合的韦伯分布理论曲线与试验结果的经验分布曲线符合良好，相关系数多在0.96以上。其示例如图3所示。

2.2.2 立波波谷压力FH/Fˉ的参数估计

同样的，根据立波的实验资料，也可分别求得不同基床上水深d1的不规则波立波波谷压力的韦伯尺度参数η和形状参数β。统计结果表明形状参数β在0.24～0.65间变化。经过拟合，韦伯分布理论曲线与实测的经验分布曲线符合良好，相关系数多在0.95以上。其拟合结果如图4所示。

虽然韦伯分布理论曲线与实测经验分布曲线符合良好，不过，还应对韦伯分布进行非参数检验，判断假设的波谷压力分布符合韦伯分布是否可接受，并最终确定该检验是否可以通过。

2.3 非参数检验

非参数检验是用来判断假设分布函数拟合优度的一种假设检验。通过对假设分布函数进行拟合，比较理论分布函数F0（x）和实测经验分布函数F（x）的差异程度，来判别假设的分布函数类型能否被接受。如果接受则认为假设正确，若是拒绝则假设不正确。

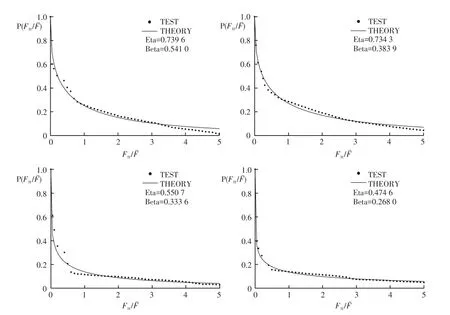
图3 破碎波压力概率分布示例Fig.3Probability distribution of breaking wave pressure

工程中假设检验的方法很多，常用的方法有Kolmogrov⁃Smjrnov检验，即K⁃S检验。该检验以经验分布函数，或者样本分布函数为检验统计量，检验理论分布函数与经验分布函数的拟合优度。过程为，找出经验分布函数F（x）和假设理论分布概率F0（x）的最大差值Dn，N足够大时，Dn服从自由度为N的Dn分布

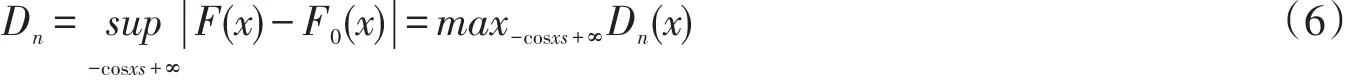
Dn分布是经验分布函数与理论分布函数的差值函数

式中：y为未知数；N为样本集；y和Dn一一对应。存在置信概率为1-α的置信区间（-Dn,a',Dn,a）

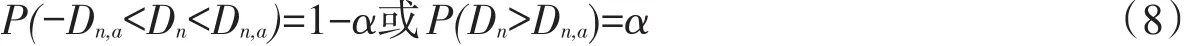
Dn,a值可查询数理统计表［13］，对于韦伯分布，按照小概率原理可知，当N≥30时，可由

求得。当Dn＜Dn,a时，则接受假设H0；当Dn＞Dn,a时，拒绝假设H0。

从上述分析可以知道，置信概率1-α愈大，Dn,a愈大，Dn＜Dn,a条件越容易满足。而且K⁃S检验没有限制条件，误差较小，分析结果精确且唯一，所以用K⁃S检验假设分布函数精度相对较高。

对上述破碎波和立波样本数据进行K⁃S检验。破碎波条件下，三组不同水深工况82组数据样本中，57组接受假设，占总样本的69%，25组拒绝假设，占31%。其中d1=15 cm工况下接受假设多，结果较好。立波条件检验结果表明，三组水深全部57组数据样本中有41组接受假设，占总体的72%，16组拒绝假设占28%。检验结果列于表2和表3中，可以看出多数是接受假设的，因此认为假设分布函数为韦伯分布是可以的。

2.4 形状参数β与影响因素的关系

得出可以用韦伯分布来描述破碎波和立波波谷压力分布后，还需求出韦伯分布的尺度参数η和形状参数β。下文针对破碎波和立波作用下，分析不同波浪要素和基床因子对形状参数β的影响，进行单因次参数分析和多元非线性回归分析。得到不规则波破碎波作用下有如下的关系式

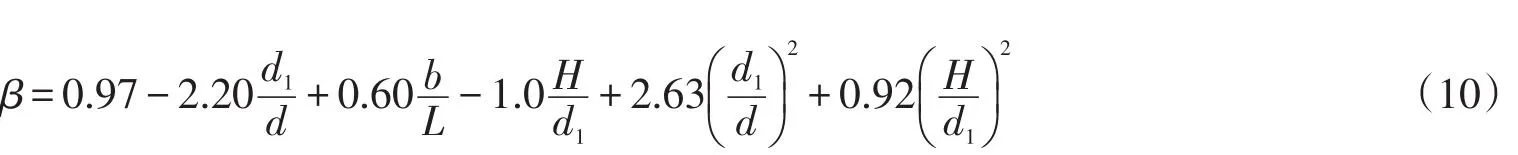
立波波谷压力分布的形状参数β可由式（12）确定

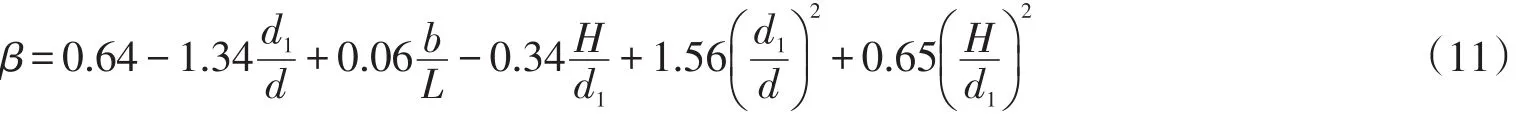
同样通过假设检验来验证经验公式的合理性。如果回归分析拟合的公式是合理的，则各实测点到拟合直线的距离Δ=||y-y*应服从正态分布。对拟合的两个样本数据分别进行K⁃S检验，采用显著性水平α= 0.05，查数理统计表［13］可得最大差值函数Dn,a，破碎波为0.147 8，立波为0.176 7。而

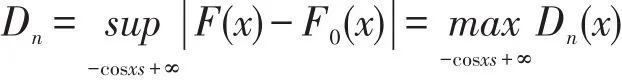
表2 立波波谷压力假设检验结果Tab.2Results of hypothesis testing in standing wave trough forces

表3 破碎波波谷压力假设检验结果Tab.3Results of hypothesis testing in the breaking wave trough forces

破碎波Dn1=0.126＜D82，0.05=0.147 8，立波Dn1=0.10＜D57，0.05=0.176 7。

因此可以认为接受假设，拟合的经验公式是合理的。

2.5 可靠性检验

对于直墙建筑物不规则波波谷压力，探求它的分布函数的最终目的是期望由分布函数F(x)找出波谷压力特征值（FH/Fˉ）的相对值，以便求出所需各特征波浪力值。此外，通过对特征波浪力值进行比较，可以判断由拟合关系式推求的形状参数β与试验分布函数的β值是否一致。计算出三个相对值，与对应的各实测值进行对比，分别为

统计分析上述3个系数可知：在破碎波波谷压力作用下，k1位于1.2～0.8之间，占总体78%；而k2位于1.2～0.8之间，占83%；k3位于1.1～0.8之间，占98%。

立波波谷压力作用下，k1位于1.15～0.91之间的数据占82%；k2位于1.10～0.81之间，占78%；k3位于1.11～0.80之间的数据占97.5%。

由此可见k3较为稳定，通过该相关系数求得各波谱的特征值不会有比较大的误差，而且c和值较为接近，说明用该值得到特征值是合适的。

3 结论

本文对直墙建筑物不规则波波谷压力进行了实验研究，测定了直墙上的破碎波波谷压力和立波波谷压力，并通过数值方法拟合了其分布函数。根据统计分布的研究成果，得出以下结论。

（1）假设相对波谷压力特征值FH/Fˉ的分布服从韦伯分布，对假设韦伯分布做参数估计，得到形状参数β和尺度参数η值。统计结果表明理论分布曲线与实验的经验分布曲线符合很好，经过非参数检验，大部分结果是接受的，说明认为压力分布服从韦伯分布是合适的。

（2）研究了韦伯分布的形状参数β与哪些因素有关，经过单因次参数分析和多元非线性回归得出β与相对波高、相对肩宽和相对水深的关系式，拟合结果较好。因此可以从波浪要素和基床条件等参数求得韦伯分布的形状参数β，进而求出尺度参数η得到波谷压力的韦伯分布。

（3）验证了可以从韦伯分布推求特征波谷压力值，经过可靠性检验表明计算值和实验值较为接近，可以用该值推求特征值。

［1］康海贵，孙英伟.近破波对直立建筑物的作用力及冲击流场研究［J］.水运工程，2010，12（3）：21-16. KANG H G，SUN Y W.Study on mechanism of breaking wave loads on vertical walls［J］.Port&Waterway Engineering，2010，12（3）∶21-16.

［2］俞聿修，李本霞，张宁川，等.斜向和多向不规则波作用于直墙堤上的波浪荷载［J］.水运工程，2011，12（1）：24-28. YU Y X，LI B X，ZHANG N C，et al.Wave loads on vertical wall in oblique and multi-directional irregular waves［J］.Port&Wa⁃terway Engineering，2011，12（1）：24-28.

［3］黄培基，赵炳来.直立堤前波浪和波压力概率统计特征［J］.海洋与湖沼，1983，14（4）∶367-378. HUANG P J，ZHAO B L.The probability characteristics of the wave and wave pressure at a vertical breakwater［J］.Oceanologia Et Limnologia Sinica，1983，14（4）∶367-378.

［4］李玉成，刘大中，苏小军，等.直墙上不规则波近破波的波浪力［J］.水动力学研究与进展（A辑），1997，12（4）∶456-469. LI Y C，LIU D Z，SU X J，et al.The Irregular Breaking Wave Forces on Vertical Walls［J］.Journal of Hydrodynamics，1997，12（4）：456-469.

［5］李玉成，刘大中，齐桂萍，等.不规则波远破波对直墙的作用［J］.海洋学报（中文版），1999，21（2）：99-107. LI Y C，LIU D Z，QI G P，et al.Irregular broken wave forces on vertical wall［J］.Acta oceanologica sinica，1999，21（2）：99-107.

［6］Cuomo G，Allsop W，Takahashi S.Scaling wave impact pressures on vertical walls［J］.Coastal Engineering，2010，57（6）∶604-609.

［7］Bullock G N，Obhrai C，Peregrine D H，et al.Violent breaking wave impacts.Part 1：Results from large⁃scale regular wave tests on vertical and sloping walls［J］.Coastal Engineering，2007，54：602-617.

［8］Rajasekaran C，Sannasiraj S A，Sundar V.Breaking wave impact pressure on a vertical wall［J］.The International Journal of Ocean and Climate Systems，2010，1（3-4）：155-166.

［9］Martinelli L，Lamberti A，Frigaard P.Effect of short⁃crestedness and obliquity on non⁃breaking and breaking wave forces applied to vertical caisson breakwaters［J］.Coastal Engineering Journal，2007，49（2）：173-203.

［10］Franco L,De Gerloni M,Passoni G,et al.Wave forces on solid and perforated caisson breakwaters∶comparison of field and labo⁃ratory measurements［J］.Coastal Engineering Proceedings,1998,1(26)∶1 945-1 958.

［11］McKenna J,Allsop W.Statistical distribution of horizontal wave forces on vertical breakwaters［J］.Coastal Engineering Proceed⁃ings,1998,1(26)∶2 082-2 095.

［12］李玉成，刘大中.作用于直墙堤上不规则波破波波浪力的统计分布特性［J］.水动力学研究与进展（A辑），1995，10（1）∶48-60. LI Y C，LIU D Z.The Statistical Characteristics of Irregular Breaking Wave Forces on Vertical Walls［J］.Journal of Hydrodynam⁃ics，1995，10（1）∶48-60.

［13］中国科学院数学研究所概率统计室.常用数理统计表［M］.北京∶科学出版社，1974.

Statistical characteristics of irregular wave trough forces on vertical walls

LUO Jun⁃bin1,SUN Zhao⁃chen2,LIANG Shu⁃xiu2,ZHAO Xu⁃dong2
（1.CCCC⁃FHDI ENGINEERING CO.,LTD.,Guangzhou 510230,China;2.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China）

This paper presents result on the random wave trough forces on a vertical⁃wall structure.The wave used in the tests is directional and irregular wave.The experiments are carried out with different foundation bed height and width,and different relative wave height.Based on the probabilistic analysis of model test data of irregu⁃lar standing and breaking wave trough loads on vertical walls,it is indicated that the probabilistic distribution can be expressed by Weibull formulation,in which the parameter β is well related to wave parameters as well as the pa⁃rameter of rubble mound foundation,and the parameter η can be obtained by the theoretical relation between β and η.The calculated results agree well with the test data.

irregular waves;vertical⁃wall structure;wave troughs forces;wave pressure distribution

TV 142；O 242.1

A

1005-8443（2015）05-0391-07

2015-01-26；

2015-04-14

骆俊彬(1987-)，男，江西省南昌人，助理工程师，主要从事波浪和建筑物相互作用的研究。

Biography：LUO Jun⁃bin（1987-），male,assistant engineer.