基于并行计算的列车运行仿真快速算法设计*

2015-06-29王志强

城市轨道交通研究 2015年6期

王志强

(苏州大学城市轨道交通学院，215006，苏州∥讲师)

基于牵引计算的列车运行仿真技术可充分利用现代计算机软硬件技术，真实、快速、准确地计算列车运行过程，为线路工程咨询、工程设计、运营管理提供强有力的科技设计手段和辅助分析与决策工具，具有重要的现实意义。然而，传统的列车运行仿真算法运算量大、运算效率低，大大限制了其应用范围。为此，本文从常规算法的缺点和不足出发，充分发挥日益普及的多核中央处理器(CPU)的运算优势，提出基于并行计算的列车运行仿真快速算法。该算法能在不影响运算精度的前提下大大提升运算效率，为拓展列车运行仿真技术的应用范围奠定基础。

1 列车运行仿真常规算法简介

1.1 列车受力分析

以单质点模型为例，列车受到的外力全部作用在质点上，包括:牵引力Fqy，基本阻力Wjz，由于曲线、坡道和隧道等产生的附加阻力Wfz，制动力Fzd，列车自身的重力Pg，线路对列车的支持力N 等(如图1所示)。

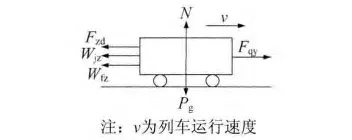
图1 列车受力分析

影响列车运行过程的外力主要有 Fqy、Wjz、Wfz和Fzd。由它们矢量叠加产生的合力，是推动列车运行状态不断变化的源泉。

1)单位牵引力fqy:其取值根据牵引特性数据(fqy=f1(v))，通过线性插值法求得任意速度点的单位牵引力值。

2)单位基本阻力wjz:根据公式wjz=a+bv+cv2求得，其中a、b、c 为与车辆有关的经验常数。

3)单位附加阻力wfz:包括单位坡度附加阻力wi(wi=i，i 为线路坡度)，单位曲线附加阻力wr(wr=A/R，其中A =600 为经验常数，R 是线路曲线半径)和单位隧道附加阻力 ws(ws=0.000 13Ls，Ls为隧道长度)三部分。

4)单位制动力fzd:根据制动特性曲线(fzd=fz(v))采取线性插值法计算任意速度的单位制动力。

1.2 列车运行中各种工况下的受力

列车运行过程中的各种工况包括:起动工况，加速工况，惰行工况及制动工况。各工况下列车所受单位合力c 如下:

1)起动工况下:

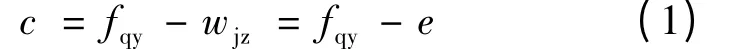
式中，e 为单位起动阻力的经验值。

2)加速工况下:

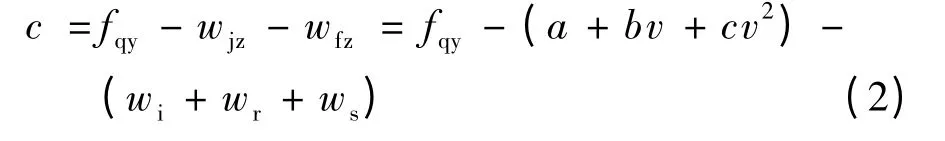
3)惰行工况下:

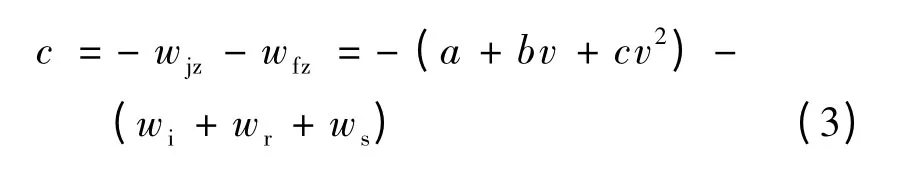
4)制动工况下:

根据所受的单位合力c，即可求得列车瞬时加速度a 如下:

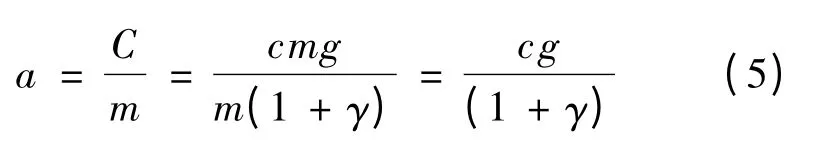
式中:

C——列车受到的合力;

m——列车总质量;

γ——回转质量系数，通常取0.06;

g——重力加速度。

然后按照式(6)所示速度－距离基本迭代计算公式，计算列车运行过程中的相关数据。

式中:

ai——第i 步长时的列车瞬间加速度;

ci——第i 步长时列车受到的单位合力;

Si——第i 步长时列车的位置;

vi——第i 步长时列车的速度;

Δt——每个步长的时间间隔。

1.3 列车进站精确制动停车判断

列车制动距离是指自制动开始到停车，列车所通过的距离。为了保证城市轨道交通列车的准确停车，必须要满足列车到达车站指定位置时速度为零。

为了确保列车进站精确停车，仿真计算过程中的每一步都需要调用算法来判断列车在当前状态(vi，Si)下若采取制动，能否满足列车到站时速度为零的要求。所以，计算过程中需要频繁调用“准确停站判断算法”，如图2所示。

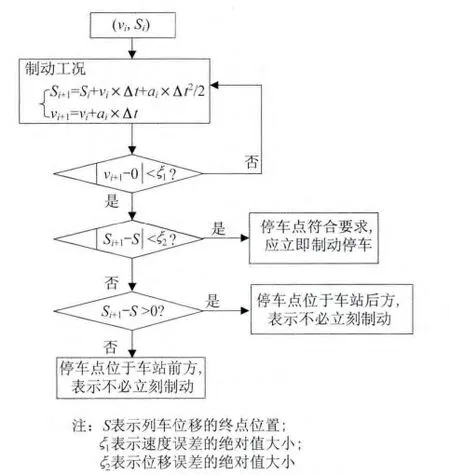
图2 列车准确停站的判断算法

1.4 列车运行仿真常规算法流程

列车运行仿真常规算法流程的具体步骤如下:

1)取得线路平纵断面、列车牵引特性、列车制动力等基础数据。

2)根据运营的限速要求和线路曲线对速度的限制要求，将列车的运行线路分成若干个限速分段，并且判断限速分段之间能否满足列车的合理过渡，即列车从限速为vi的分段向限速为vj的分段过渡时列车制动能力能否满足要求。

3)初始化列车的速度、位移、时间等相关参数。

4)计算在列车起动过程中，每一个步长时间内的列车速度值、时间值和位移值，并将数据保存。

5)判断列车在下一个步长内，如果采取牵引工况的话，能否满足列车制动准确停站的要求。如果满足条件，则计算列车在下一个步长内牵引工况下的列车速度值、时间值和位移值，并将数据保存;反之，则转步骤6)。

6)判断列车在下一个步长内，如果采取惰行工况的话，能否满足列车制动准确停站的要求。如果满足条件，则计算列车在下一个步长内惰行工况下的列车速度值、时间值和位移值，并将数据保存;反之，则转步骤7)。

7)计算列车在下一个步长内制动工况下的列车速度值、时间值和位移值，并将数据保存。

8)判断列车是否到达终点，如果是，则转步骤9);反之，则转步骤5)。

9)将每个步长内计算得到的列车运行数据在图上表示出来，并用短直线连接，以形成列车牵引的速度－距离(v－S)曲线和时间－距离(T－S)曲线。

根据上述常规算法的计算流程，不难发现该算法存在以下不足:

1)仿真算法采用单线程顺序计算，列车只能从起点开始，按照里程依次前行，途径沿线的各个区间和车站，最后到达终点。

2)计算过程中的每一个仿真步长都需要进行1 至2 次的制动起点反向推算，才能判断出拟采用的牵引工况是否满足要求。而每次的制动起点反向推算，都需要调用图2所示的反向递推试凑算法来寻找制动起点。这就使得算法的计算量非常巨大，计算过程耗时很长，不利于实时仿真的实现，也限制了列车运行仿真技术的推广应用。

2 对常规算法的改进

为了克服上述常规算法的不足，本文在下述两方面对常规算法进行了改进。

2.1 变单线程顺序计算为多线程并行计算

充分利用日益普及的多核CPU 的计算优势，将线路上每个区间的列车运行过程拆分为一个独立的运算单元，实现各区间的列车运行过程并行计算，待所有区间运行过程完成之后，再将计算数据汇总和处理。

图3所示为常规算法的顺序计算流程，按照里程顺序依次计算各区间的运行数据，抵达线路终点后仿真计算完成。

图3 单线程顺序计算的流程示意图

图4所示为本文采用的并行计算算法流程。因各区间的运行过程被当做一个独立的运算单元，因此与图3所示的顺序计算流程相比，并行计算在计算开始前的准备和计算结束后的处理上均有所不同。

图4 多线程并行计算的流程示意图

1)计算开始前的准备工作:将各运算单元的列车初始位置设为区间起点车站的中心线位置，列车初始速度设为车站控制速度，初始仿真时钟设为零。

式中:

si，0，vi，0，ti，0——分别为第 i 个运算单元的列车位移、列车速度和仿真时间的初始值;

si，s1，vi，s1——分别为第 i 个运算单元所对应的区间起点车站的中心线位置和该起点车站所规定的车站控制速度。

2)计算结束后的处理工作:按区间里程顺序，按式(8)所示的换算规则，依次收集各区间的运行数据，得到完整的全线列车运行仿真数据。

式中:

sk，vk，tk——为汇总后的第 k 组计算结果数据中的列车位移、列车速度和仿真时间;

si，j，vi，j，ti，j——为第 i 个运算单元的第 j 组计算结果数据中的列车位移、列车速度和仿真时间。

与顺序计算一样，并行计算忽略了列车每次抵达区间终点站时产生的位置误差和速度误差，即每次列车开始从区间起点站出发时，其位置和速度都默认为起点车站规定的标准值。

与顺序计算相比较，并行计算虽然在计算开始前的准备和计算结束后的处理上有额外的工作，但从式(7)和式(8)可知，其主要是简单的赋值运算。因此，并行计算的综合效率要远高于顺序计算。

2.2 大量减少制动起点反向推算的次数

采用预先计算制动曲线的方法，当列车v－s 坐标点远离制动曲线时，只进行限速要求判断不进行制动起点推算;当列车v－s 坐标点接近制动曲线时，才启动制动起点推算，以寻找最佳的制动起点。

如图5所示，常规算法的制动起点反向推算需列车从A 站出发时起，至列车v－s 曲线点抵达制动曲线时止，其推算运行距离如图5 中的L常规。

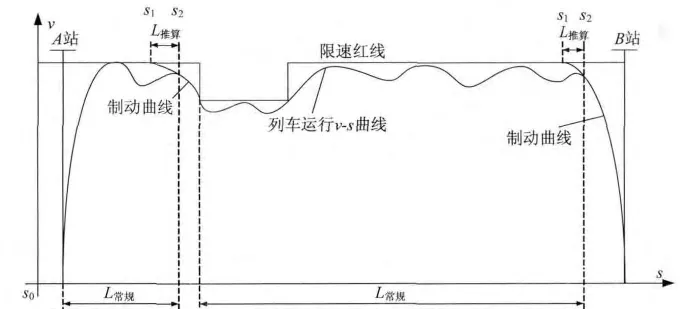
图5 减少制动起点反向推算次数的技术示意图

从图5 中可知，大量的反向制动推算工作是没有必要的，只有当列车v－s 曲线点靠近制动曲线时，才有必要进行制动反向推算。为此，可从制动曲线与限速红线的交点所对应的距离s1处开始进行反向推算，则所需的推算距离为图5所示的L推算，其远小于L常规。从而大大减少了列车运行过程中的制动起点反向推算次数，减少了计算量，大大地提升了列车运行计算的速度。

3 改进算法的计算流程

3.1 总体流程

在图6 中，与常规算法的流程一样，首先进行基础数据的读取和限速分段的划分;然后，按照区间数量划分运算单元，列车在每个区间的单向运行过程被划分为一个独立的线程运算单元;再后，主线程将各个区间范围内的线路基础数据、限速要求数据和列车性能数据传递给对应的线程运算单元，做好启动计算前的准备工作;接着，主线程给每一个线程运算单元传达启动计算命令，并不断侦听各线程运算单元的计算进度，直至所有线程运算单元完成计算;最后，主线程收集各线程运算单元的计算结果，并进行处理和汇总，得到全线路范围内的列车运行仿真数据，并将其保存后绘制v－s、t－s 曲线，结束本次计算。

3.2 运算单元算法流程

在图7 中，线程运算单元首先接收到主线程传递来的线路基础数据、限速要求数据和列车性能数据，并找出区间内每个速度控制点的控制位置和控制速度;然后，按照反向递推法求出每个速度控制点对应的制动曲线，找出该制动曲线与限速红线的交点，并记录其位置信息s1，i。接着，将列车初始位置设为区间起始车站的中心线位置，将列车的初始速度设为区间起始车站的控制速度，将仿真时钟设为零，并开始仿真计算;在每一个仿真步长内，首先判断列车当前位置 sk是否小于 s1，i，若 Sk＜ s1，i，则列车在下一步长工况选择时，只需判断是否满足限速红线要求即可，无需进行制动起点推算;反之，若sk≥s1，i，则列车在下一步长工况选择时，需要进行制动起点推算，判断是否同时满足制动停车和限速红线两个要求;最后，当列车到达区间终点车站的中心线位置时，保存仿真数据并结束计算。

图6 基于并行计算的列车运行仿真算法流程图

4 算例效果

图8所示为采用改进算法的一个列车运行仿真效果实例图。图8 中设有10 个车站，A 站～J 站，选用编组相同的列车进行追踪运行，仿真步长取0.1 s，其它参数略。列车从A 站起动到J 站停车，在中间各站均停车30 s，列车的运行曲线如图8所示。在i7－920(2.66 GHz 四核八线程)的微机平台上，在计算参数完全相同的条件下采用改进算法完成本次运算共用时6.2 s，而常规算法完成本次运算则耗时274 s。可见，本文所述的并行计算方法在多核CPU平台上的计算效率要远高于常规算法，且其效率的提高值随着CPU 内核数的增加而增加。