EM算法在不完全高程测量数据处理中的应用

谭雄辉 肖琴琴 刘宇健 谭意泷 胡 涌

（湖南城市学院,湖南 益阳 413000）

EM算法在不完全高程测量数据处理中的应用

谭雄辉 肖琴琴 刘宇健 谭意泷 胡 涌

（湖南城市学院,湖南 益阳 413000）

本文分析了EM算法在不完全高程测量数据中的实现方法，推导了EM算法进行测量数据处理的方法步骤，通过具体实例实现了EM算法在不完全测量高程数据处理中的应用。最终结论表明，不完全测量高程数据通过采用EM算法并结合精密平差方法进行处理，提高了测量成果的精度，与完全数据下的平差处理结果非常接近，而与直接平差法处理的结果相比有明显的优势。

EM算法 最小二乘原理 不完全测量数据 平差

1 引言

在测量工作的开展过程中，由于各种不利因素的影响，导致采集到的有用数据不够多。为了提高测量成果的精度，往往需要进行一些多余观测或补测，但是现在社会发展迅速，由于生活生产所需，各种建筑物拔地而起，或者受到天气自然灾害的影响，一些重要的控制点会遭到破坏或者被掩盖掉，导致无法进行多余的观测或者补测。或者即使有用数据够多，但随着时间的变迁，一些观测数据丢失或遭到破坏。这此情况都会造成数据不完全，对这些数据进行处理，会严重影响成果的精度，甚至导致所有的观测数据都不可用，这是一种极大的浪费。为了减少损失，通常要对不完全数据进行一些处理，比较常用的有删除法、预测法、拟合法或填补法等[1]，以此来提高精度。但这些数据的可靠性有限，采用它们来进行参数估计就会出现更多的问题。EM（Expectation Maxinization）算法[2,3]作为一种处理缺失数据的经典方法，它在许多领域有着很好的应用。因此本文将EM算法与常规测量数据处理方法相结合，推广到不完全高程测量数据的数据处理中，来提高高程测量成果的精度[1]。

2 EM算法在不完全高程测量数据中的应用

EM算法是一种处理不完全观测数据较有效的方法，它主要应用于非完全测量数据的参数估计，通过计算缺失测量数据的条件期望，并将其极大化，通过充分地利用有益于数据处理的潜在数据，有效提高了数据处理的质量并简化计算，提高数据成果的精度[2]。

EM算法采用G-M (Gauss-Markov)模型处理测量数据[4,5]，在测量数据的处理过程中，它与间接平差法结合，经过E步和M步循环直至待估参数小于某个满足精度要求的值即可，迭代计算结束后，即可求得基于不完全测量数据下未知参数的最大似然估值，从而提高高程测量成果的精度。

3 实例分析

以湖南城市学院电信楼周边的四等水准测量为例，如图1所示，A为已知高程点，其高程为HA=50.000m，可视为无误差的高程点，为了得到C点及D点的高程，共进行了六次测站观测获得6个高差观测值， h1=-2.456m，h2=-0.334m，h3=-0.454m,h4=+1.360m，h5=+1.240m,h6=+0.650m。

在正常情况，即所有的观测数据h1、h2、h3、h4、h5、h6都能使用的情况下，我们可以采用最小二乘原理及间接平差法，得到HC、HD的高程分别为：HC=47.208m，HD=46.752m。

图1 水准测量简易路线

现假设由于某种因素如管理人员保存数据不当，导致h3观测数据丢失，从而造成测量数据不完全，而由于电信楼周边建筑的修建导致测量工作开展困难，此时要得到两个未知点的高程值，就不能采用常规的最小二乘平差方法和间接平差法来计算，只能采用直接计算法得到HC、HD的高程为：HC=47.210m，HD=46.750m。然而在测量过程中，由于各方面的因素导致观测数据存在一定的误差，由这样的观测值得出的高程值精度难以满足要求。

现引入不完全数据的经典处理方法EM算法进行测量数据的处理，通过不完全测量数据简单计算得到HC、HD的初始值为HC=47.210，HD=46.750。积分取值空间选择为0.440—0.470，即由初始值计算的高差上下浮动15mm。使用matlab进行编程迭代计算，可得到HC、HD的高程分别为：HC= 47.2083m，HD= 46.7517m，各种数据处理方法的结果见下表1，而各种方法结果的比较见下表2。

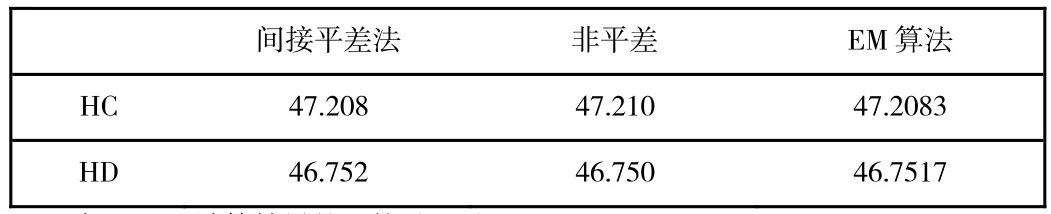
表1 计算结果（m）

表2 计算结果的比较（mm）

从表1和表2中我们可以看出，当数据不完全时，对测量数据进行处理的方法中，EM算法与完全数据时的间接平差法得出的C、D点高程值较为接近，均相差0.3毫米，而直接计算法得出的C、D点高程相差得较远，均为2毫米。这主要是因为在外业观测的过程中，由于受到仪器，观测者和外界环境的影响，观测数据中存在一定的误差。采用直接法进行计算必然使得未知点的高程携带这些误差，而EM算法挖掘出了一些隐藏的数据信息，结合间接平差法来对这些误差进行处理，进一步提高了未知点高程的精度。由此可知，当测量数据出现缺失时，结合EM算法与完全数据时精密平差方法来处理测量数据可有效地提高高程测量成果的精度。

4 结论

在处理测量数据时，采用合适的精密平差方法会尽可能地减少误差，提高测量成果的精度。而精密平差法往往需要一定数量的多余观测量才能达到较好的效果。而在实际测量中，观测量不足或缺失的问题却会经常遇到，如各种因素的影响导致高程观测数据量不够多，部分采集到的高程数据因质量太差不可用，或是观测后的保存处理不当等导致的部分数据丢失。因此就不能采用常规的数据处理方法，不然得出的结果可能不是最好的。本文通过具体实例，将EM算法引入至不完全的高程测量数据处理的方法中，在高程测量数据不完全的情况下挖掘出有用的潜在数据，结合精密平差法来处理不完全的观测数据。结果表明，EM算法的加入能有效地提高高程测量结果的精度。这样在各种工程项目中，有一些废弃的观测数据可以通过引入EM算法来重新得到使用，提升了数据的价值。当然，EM算法还存在一些不足，如当缺失较多数据时，它的效果并不是很明显，值得再进一步深入研究。同时EM算法不能仅仅局限于高程测量的数据处理，它在测量其它方面的运用也值得我们进行研究。

[1]林东方. 基于EM算法的不完全测量数据的处理方法研究[D].中南大学,2012.

[2] 张宏东. EM算法及其应用[D].山东大学,2014.

[3] 曾传璜,,张鑫,,张晶晶.EM算法的研究[J]. 软件导刊,2008,7(9):97-98.

[4] 肖琴琴,宋迎春,杜琨. EM算法在广播星历计算卫星位置中的应用[J]. 测绘工程,2013,06:73-76+85.

[5] 杜琨,宋迎春,肖琴琴. EM算法在卫星轨道计算中的应用[J]. 全球定位系统,2013,02:41-44.

G322

B

1007-6344（2015）04-0304-01