对基坑监测中混凝土支撑轴力计算公式的修正
2015-06-28赵湘伟唐曾智
赵湘伟,唐曾智
(解放军理工大学国防工程学院, 江苏南京 210007)
对基坑监测中混凝土支撑轴力计算公式的修正
赵湘伟,唐曾智
(解放军理工大学国防工程学院, 江苏南京 210007)
为保证深基坑的安全,需要对基坑进行监测。监测过程中会产生大量的数据,处理这些数据是一项工作量非常大的任务,为此可以利用计算机程序帮助分析数据,但前提是必须要有统一具体的计算公式。在研究了传统的支撑轴力计算公式运用于计算机程序处理数据时遇到的问题的基础上,得出了一种更适合支撑实际受力情况的轴力计算公式。
钢筋混凝土; 支撑轴力; 监测; 计算机程序
1 基坑监测中混凝土支撑轴力常用计算公式
支挡结构主要是指施工过程中用来保证施工安全的支撑与围护结构体系。支挡结构主要采用钢筋混凝土和钢结构。钢筋混凝土围护支挡构件,其内力或轴力通常是通过测定构件受力钢筋的应力,然后根据钢筋与混凝土共同工作、变形协调条件计算得到。对于采用钢筋计测量钢筋应力后反算支撑轴力,基坑监测中常用的轴力计算公式为:
(1)
对于由式(1)计算出的轴力,在基坑监测运用计算机处理数据时存在以下一些问题。式(1)是在理想状态下,即支撑全面受压,用钢筋应力计测得的都是压应力,不会产生拉应力,在这种条件下用式(1)计算轴力是准确的。但是在实际工程中,发现用钢筋应力计测的往往出现拉应力,此时再直接用该式计算轴力显得不是那么明智,不能很好的反映支撑的真实受力,继续按该式计算出的轴力指导施工会给施工安全造成一定的风险。
2 支撑轴力计算探讨
针对以上几个问题,本文做了以下一些探索:(1)当实测断面均为压应力时,仍然采用式(1)计算支撑轴力。(2)当实测断面的应力值异号时,可对式(1)进行修正。理论上,监测支撑轴力时不会有拉应力出现,但是由于支撑本身的重量以及其它未知荷载的作用等很多因素,会导致拉应力的产生。但若将横支撑看作一根梁,那么一般地认为如有拉应力的产生,则只可能是产生在支撑截面的下部。这里又分两种情况讨论,一种是出现拉应力,但下端混凝土未开裂,另一种是出现拉应力且下端混凝土开裂。
2.1 混凝土开裂前轴力计算公式
本文探讨在考虑弯矩和轴力共同作用下,支撑轴力的计算公式的修正。设由支撑轴力单独作用产生的应力为:
(2)
设弯矩为M,由弯矩产生钢筋的压应力为σM1、拉应力为σM2,并假定:
(3)
所以实际测得的钢筋应力应为:
(4)
(5)
式中:σcs表示受压应力;σts表示受拉应力。
由式(3)~式(5)得:
(6)
由式(2)、式(6)得
(7)
文献[1]对纯弯作用下梁截面的应力应变进行了实验研究,发现以下几点:
(1)梁下部混凝土产生裂缝前,弯矩对梁截面的应力应变图形的中和轴基本位于梁的中部(图1)。即混凝土产生裂缝前,弯矩对受压钢筋和受拉钢筋产生的应变值近似相等,故此处a取1,则式(7)化为:
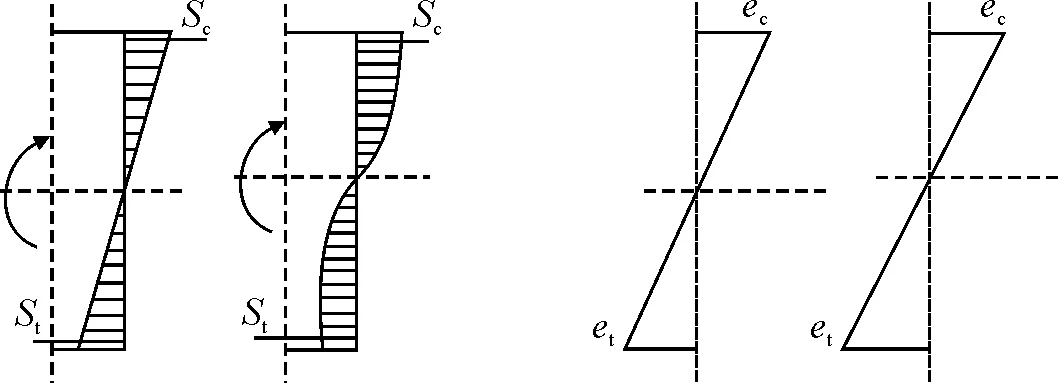
(a)应力图 (b)应变图 图1 混凝土产生裂缝前梁截面的应力应变图
(8)
(2)若混凝土开始产生裂缝,理想应力应变图如图2,但实际应力应变图不是如此,由实测的σcs、σts反算出应变值εcs、εts,绘出实测应力、应变曲线如图3所示。这种情况下,式(3)中a值不好确定,故用上面的计算方法已经不能得出支撑轴力的计算公式。下面本文将从截面开裂后实际受力状态以及实测的钢筋应力分析得出支撑轴力的新计算公式。

(a)应力图 (b)应变图 图2 混凝土开裂前后的应力应变对比
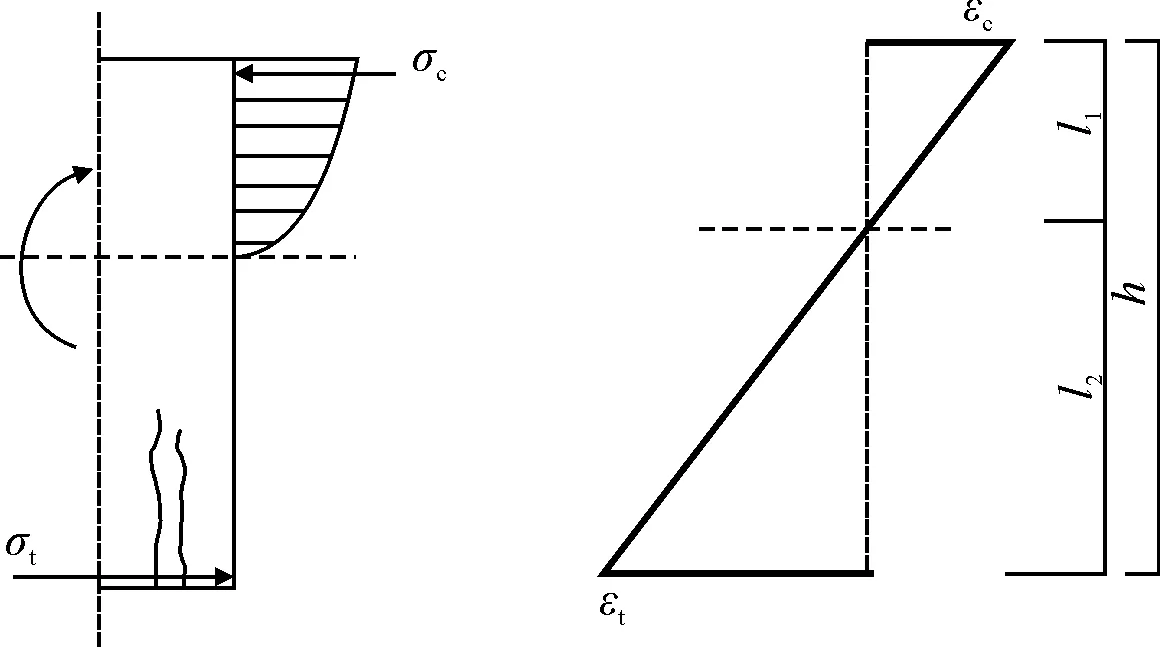
(a)应力图 (b)应变图 图3 由实测值绘制的梁截面的应力应变图
2.2 混凝土支撑开裂后的轴力计算公式
首先应对混凝土是否产生裂缝进行判断,根据实测钢筋应力σts反算出应变εts,由混凝土与钢筋协同工作产生应变相等即εtc=εts,再由以下公式进行判断:
(1)当εtcEc≤ft时(ft为混凝土抗拉强度设计值),混凝土未开裂采用式(8)计算合适。
(2)当εtcEc>ft时,混凝土开裂,开裂区混凝土退出工作,此时需要对截面重新分析受力得出计算公式。
我们知道,在混凝土开裂后截面上会发生应力重分布,中和轴上部混凝土受压,下部混凝土未达到开裂应变的部分受拉,开裂部分退出工作。此处仍假定图3(a)中受压混凝土和中和轴下部分未开裂的混凝土应力图近似为三角形分布。为计算混凝土支撑轴力,以中和轴为x轴,截面高为y轴建立直角坐标系,如图4所示。

图4 建立的直角坐标系
则可得曲线的方程为:
(9)
其中:εcc、εtc分别为梁上部边缘和下部边缘混凝土的应变,它们分别和εcs、εts相等,所以式(9)又可改写为:
(10)
由式(10)可知:中和轴上受压混凝土距中和轴距离:
(11)
未开裂受拉混凝土距中和轴距离:
(12)
故受压区混凝土受力:
(13)
受拉区混凝土受力:
(14)
式中:h、b分别为截面的高度和宽度。
由式(13)、式(14)及轴向方向的平衡条件可知支撑轴力N为:
(15)
式中应力带符号运算,压应力为正,拉应力为负。
3 结论
通过分析基坑支撑轴力监测中轴力计算遇到的实际问题,解决了传统轴力计算公式在适用范围上具有局限性的问题。在实际监测中要根据监测到的数据判断支撑混凝土是否开裂,未开裂时一律采用传统计算公式,开裂后则要用式(15)更符合支撑实际工作时的受力情况。式(15)的提出为计算机编程处理数据提供了计算公式,省去了监测人员大量处理数据的时间,提高了工作效率。
[1] 车宏亚,江见鲸.混凝土结构[M].中国建筑工业出版社,1999
[2] GB 50010-2010混凝土结构设计规范[S]
[3] 夏才初,李永盛. 地下工程测试理论与监测技术[M]. 同济大学出版社,2002
[4] 梅英宝,朱向荣. 关于地下结构轴力监测方法的一点看法[J]. 工业建筑,2003,33(2)
[5] 叶万灵. 围护结构中钢筋混凝土支撑轴力和变形的研究[J]. 水运工程,2000,32(9)
[6] 李永盛,夏才初,潘国荣. 土木工程监测技术[M]. 中国建筑工业出版社,2001
[7] 蔡书勇. 基坑监测中混凝土支撑轴力的相关问题研究[J].科技资讯,2012,(27):50-51
赵湘伟(1988~),男,硕士研究生,研究方向:防灾减灾及防护工程。
TB21; TU94+2
A
[定稿日期]2014-09-23
