海南沿海木麻黄可加性生物量模型1)

杨众养 薛杨

(海南省林业科学研究所，海口，571100)

刘宪钊

(中国林业科学研究院资源信息所)

王小燕 林之盼

(海南省林业科学研究所)

森林是地球上最重要的碳库之一，储存了陆地生态系统65%～98%的有机碳。森林光合作用和呼吸作用与大气之间每年的碳交换量占陆地生态系统年碳交换量的90%，在全球碳循环、碳平衡、减缓温室效应以及调节全球气候等方面起着不可替代的作用［1］。森林生物量的大小是评价森林碳循环贡献的基础［2-3］。测定森林生物量，不仅耗费大量资源，而且对森林的破坏较大，因此，确定一种合理有效的森林生物量估测方法很有必要。生物量回归模型估计是目前广泛采用的一种估算生物量的方法，该方法利用某一树种生物量的实测数据，与林木易测因子(如胸径、树高等)建立统计回归关系模型［4-5］。虽然在建模过程中，需要砍伐样木测定生物量，但是模型一旦建立，就可以利用现有样木信息估计该林分的生物量，而且有一定的精度保证。

木麻黄(Casuarina equisetifolia)是海南省沿海的主要造林树种，其种植面积已超过6万hm2，对海南省沿海岸生态系统恢复、改善和保护起着重要的作用，在防风固沙、改良土壤、改善沿岸生态环境和恢复沿海退化生态系统等方面的作用更为突出［6］。在全球气候变化和森林多功能利用的背景下，木麻黄防护林碳汇能力的发挥越来越受到森林经营者的关注和重视，因此，研建木麻黄生物量估算模型，实现木麻黄防护林碳储量估测和评价，对于森林多功能经营的指导具有重大作用。

对于木麻黄生物量估计模型的研究，前人也做了部分相关研究［7-8］。洪元程等［9］利用直线方程、对数方程、幂函数方程和指数方程4种数学方程估测东南沿海木麻黄各部分生物量，发现不同的方程估测不同部分的生物量精度不同。但是这些研究大部分都是针对东南沿海分布区的木麻黄人工林，而且研究中都是对树干、树枝、树叶、树根各部分生物量进行独立估计，这样就会导致各部分生物量估计值的和不等于总生物量估计值。一般认为各部分生物量估计值的和应该要与总生物量估计值一致，即可加性［10］。因此，本研究利用海南沿海分布区的木麻黄人工林为研究对象，建立生物量估算模型，并保证生物量估算模型的可加性。

1 研究地概况

选择海南省国营岛东林场为研究区，林场位于海南东北部的文昌市境内，地理坐标为110°36'～111°01'E，19°40'～20°06'N，面积 1.2 万 hm2。岛东林场属于沿海平原地带，地形由西南向东北稍为倾斜，沿海岸线向内陆纵深方向海拔逐渐升高，大部分地区海拔在5～20 m，最高海拔70 m。整个地貌平坦广阔。岛东林场属热带北缘沿海地带，具有热带和亚热带气候特点，属热带海洋季风气候，终年无霜，少严寒，四季常青，日照充足，气候温和。年平均气温 23.9 ℃;极端低温 0.3～6.6 ℃，出现在 1 月份;＞10℃积温为8 474.3℃。年日照时间1 953.8 h。干湿交替明显，蒸发量1 900 mm，降水量1 721.6 mm。该区主要树种有:木麻黄、湿地松(Pinus elliottii)、桉树(Eucalyptus robusta)、马占相思(Acacia mangium)、大叶相思(Acacia auriculiformis)、厚荚相思(Acacia crassicarpa)、加勒比松(Pinus caribaea)、少量龙眼(Euphoria longan)和琼崖海棠(Calophyllum inophyllum)。其中，以木麻黄为绝对优势树种，占到林场树种比例的79%。

2 研究方法

2.1 数据的获取与整理

在海南省岛东林场近海岸地带的木麻黄防护林后沿(限制性采伐区)设置不同生长阶段的木麻黄临时样地(圆形，R=5.64 m)46个，测量样地内林木的胸径和树高。选择标准木时，按胸径和树高两项主要因子进行控制，分别在不同径阶和不同树高等级选取标准样木。标准样木应选择生长正常，没有发生断梢、分叉的树木，且其冠幅、冠长也基本具有代表性，避免选择林缘木和孤立木。

伐倒样木:采用“分层切割法”取样。综合考虑树枝所处位置及其大小和数量，将树冠分上、中、下3层，先将死枝挑选出来，称其总质量;然后分别称取各层带叶活枝(含花、果，下同)的总鲜质量。从每一层枝条中选取大小和长度居中、生长良好、叶量中等的3个标准枝，将标准枝摘叶(含花)后，分别称其枝质量和叶质量，再根据每层标准枝，枝、叶鲜质量的比例和各层枝叶总鲜质量，推算每层的枝、叶鲜质量以及整个树冠的枝、叶鲜质量。在每层标准枝的重心位置左右，截取500 g以上的样品，准确称其鲜质量;将各层标准枝所摘的树叶混合后，选取500 g以上的样品，准确称其鲜质量;再在死枝中选取中等大小的枝条，从中部截取500 g以上的样品，准确称其质量［11］。

带皮树干采样:在树高 1/10、3.5/10、7/10 处两边分别锯取2个3～5 cm厚圆盘(用A、B标识，下、中、上共6个)，质量不得少于500 g。树干较大(如直径大于30 cm)时，只需靠下侧锯1个圆盘，然后再截取角度30°以上的2个扇形块(扇形块的2条边线要相交于圆盘的髓心);树干较小(如直径小于6 cm)时，只需以树高 1/10、3.5/10、7/10 处为中点，各截取一个圆盘或一段树干作为样品。分别称圆盘鲜质量;

根的采样:在根系全部挖出后，分别根茎(主根)、粗根(直径≥10 mm)、细根(2 mm≤直径＜10 mm)称其鲜质量;

将叶、枝、干、根样品分别装入密封袋中，带回实验室，在85℃恒温下，烘12 h或24 h称质量(直径10 cm以下样品和树皮、树叶样品烘12 h，直径10 cm以上样品烘24 h)，求样品干鲜质量比，然后将各器官鲜质量换算成干质量，统计并计算每一样木各器官生物量和全株树木的生物量。

本文共选取样木46株，为了更好地对木麻黄生物量数据进行模型模拟和验证，随机选取30株树木作为建模数据，剩下16株树木作为验证数据。数据详细统计信息见表1。

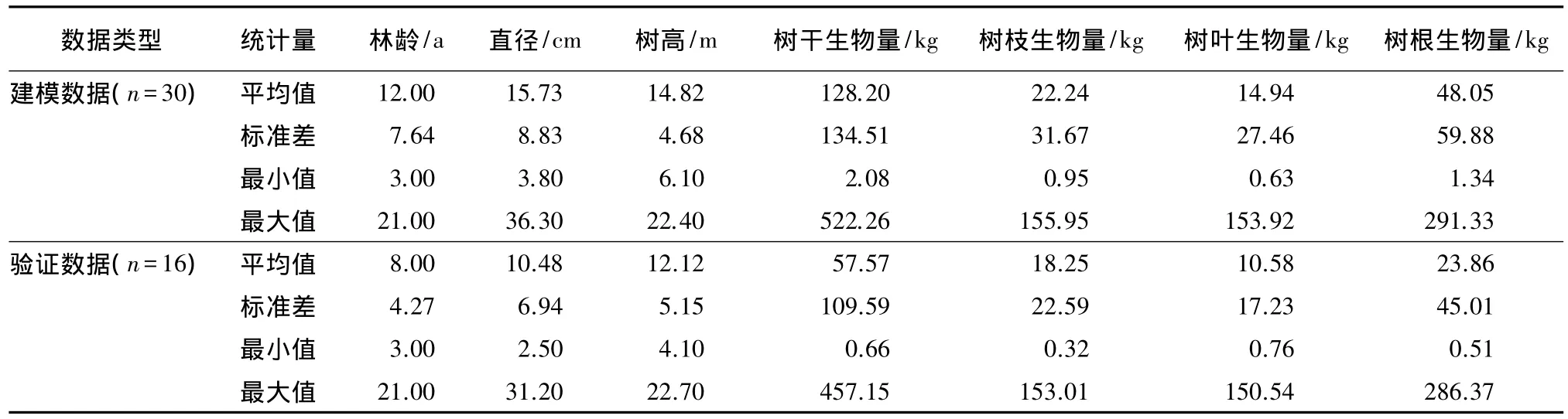
表1 木麻黄测树因子及各部分生物量统计

2.2 建模方法

目前，在生物量模型的研究可采用多种模型形式，有幂函数模型和指数函数模型等，而且模型中的自变量有胸径(D)、D2、树高(H)和 D2H 等［12-14］。以海南省沿海木麻黄生物量数据进行模型拟合，选取了6种常用生物量模型，具体表达式见表2。

表2 6种常用生物量模型

首先利用上述6种常用生物量模型对木麻黄人工林各部分生物量近行分别拟合，选出模型拟合精度最高的模型，并根据这最优模型构建木麻黄可加性生物量估算模型。

假设选出的木麻黄树干生物量模型(Wt)、树枝生物量模型(Wb)、树叶生物量模型(Wl)和树根生物量模型(Wr)的最优模型分别为:Wt=ft(D，H);Wb=fb(D，H);Wl=fl(D，H);Wr=fr(D，H)。则根据生物量可加性原则［15］，木麻黄单株总生物量模型为:WT=ft(D，H)+fb(D，H)+fl(D，H)+fr(D，H)。

对于可加性生物量模型，利用SAS软件中的PROC MODEL模块中的SUR函数建立模型并进行联立估计完成［16］。

2.3 模型选择

对幂函数模型和指数函数6种模型可以通过拟合统计量和验证统计量确定系数(R2)、均方根误差(RMSE)和平均偏差(MD)进行模型选择。其数学表达式分别为:

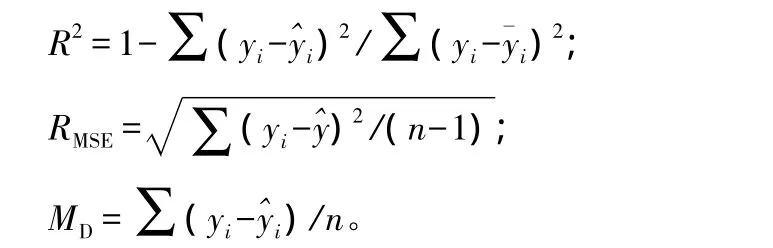
式中:yi为实际值(木麻黄各部分的生物量实测值);^yi、珋yi分别为它们的预测值和平均值;n为观察个数。

3 结果与分析

以海南木麻黄实测生物量为因变量，采用6种常用数学模型进行回归拟合，共得到木麻黄单木各器官生物量估算模型24个(见表3)。以决定系数(R2)和均方根误差(RMSE)作为模型拟合效果评价指标选择最优模型。拟合结果表明，24个不同生物量模型的 R2为 0.751 1～0.977 5，RMSE为 5.499 9～65.985 6，而且F 检验达到极显著水平(P＜0.01)，但是不同模型的拟合效果差异很大(见表4)。

表3 木麻黄人工林各部分生物量模型参数估计值

由表4可知，在模型模拟中，模型3的R2均值最高(0.951 6)，RMSE均值最小(11.793 2)，其次为模型 1，其 R2均值为 0.936 8，RMSE均值为 12.590 8，模型6拟合精度最低，其R2均值为0.876 5，RMSE均值为25.238 2。而且，在模型验证中也发现，模型3的RMSE均值最小(9.597 1)。综合模拟精度指标R2值和RMSE值，模型3的拟合效果最好。因此，接下来以模型3为基础，构建木麻黄可加性生物量模型。

基于方程W3，在建模数据中木麻黄可加性生物量模型的拟合效果较好，木麻黄可加性生物量模型调整的R2值在0.908 9～0.980 6之间，尤其是总生物量模型的预测精度最高(见图1)。相对于各部分生物量模型独立估计时，利用联立估计建立的可加性生物量模型的拟合精度略有下降。其中，树干生物量模型独立估计时，R2值为0.977 5，而联立估计时，R2值为0.974 3;树枝生物量模型独立估计时，R2值为 0.954 3，而联立估计时，R2值为 0.945 6;树枝生物量模型独立估计时，R2值为0.925 9，而联立估计时，R2值为0.908 9;树根生物量模型独立估计时，R2值为 0.948 7，而联立估计时，R2值为 0.951 1。但是，总体上拟合精度差别不大。重要的是利用联立估计建立的木麻黄可加性生物量模型更符合逻辑，实用性更强。

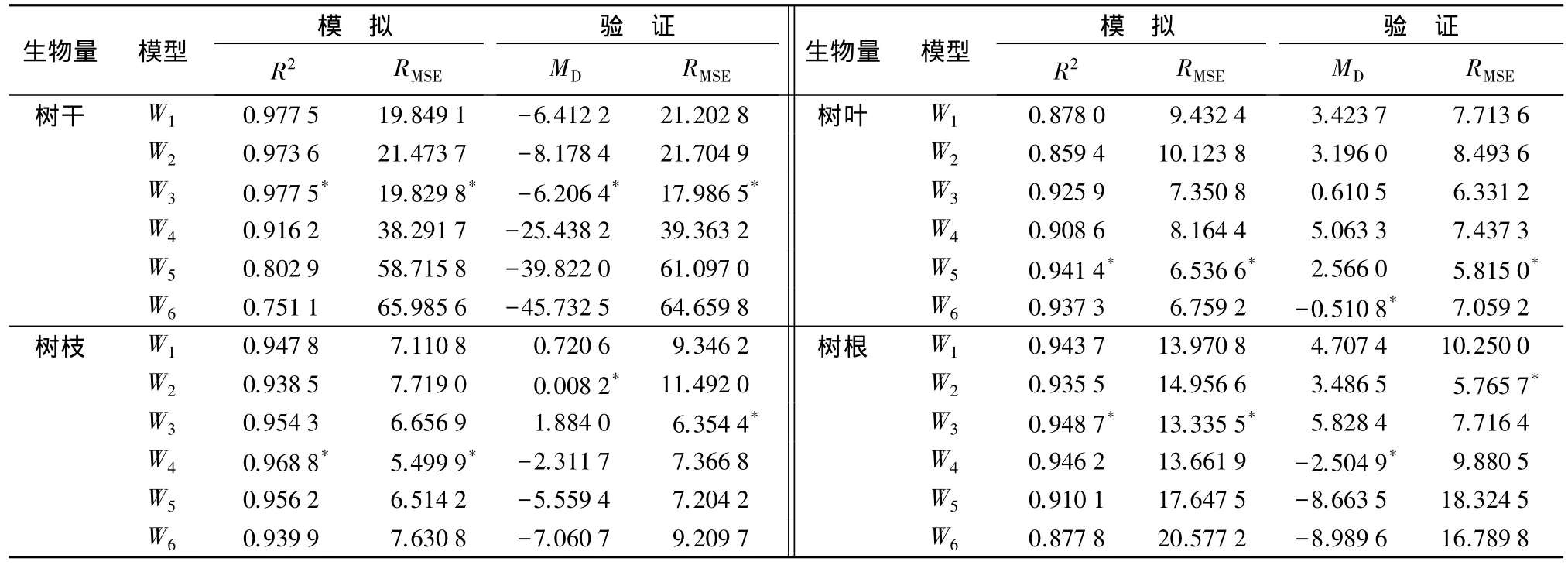
表4 6种模型拟合优度和验证效果

图1 木麻黄可加性生物量模型估计值与实际值的相关性

4 结论与讨论

本文在建立海南木麻黄生物量估算模型时，采用幂函数和指数函数6种数学模型进行拟合，共得到24个模型拟合值。以幂函数为基础的模型拟合效果较好，而且综合模型拟合精度以W3的拟合效果最好。洪元程等［9］在估计东南沿海木麻黄人工林生物量时，发现幂函数方程的拟合效果相对较好，这与本研究的结论一致。不同地区的木麻黄人工林土壤条件、气候条件、林龄、林分密度、经营措施等均存在不同程度的差异。根据树木异速生长理论，相同的方程生物量的估计会有所不同［17］。因此，我们在建立生物量模型时，为保证模型的模拟精度尽量要考虑模型的适用性。对于生物量模型自变量的选择，主要与植物的自身形态有关［18］，同时也要兼顾到实用性和简便性的原则［19］。有学者认为，胸径是建立树木各部分生物量模型的最佳自变量，增加树高自变量，有时候并不能使模型的拟合精度增加［20-21］。然而，也有人认为，增加树高自变量，可以有效地提高树木各部分生物量和总生物量的预测精度［22-23］。这与本研究的结果一致。

根据上述选择的最优模型W3为基础，建立木麻黄生物量可加性模型。该可加性模型的拟合精度较高，R2值大都高于0.9。在考虑建立树木不同部分的生物量模型时，必须考虑生物量模型的可加性。虽然该原则常被一些学者提到，但是仍然还有学者忽略这个问题［24-25］。而且由于各部分生物量之间存在着一定的相关性，若对这些模型进行独立估计，会产生系统偏差［26］，而采用联立估计则会解决系统偏差，保证参数估计的有效性。因此，本研究利用联立估计法，建立木麻黄可加性生物量估计模型，减少了系统误差所带来的估计偏差，提高了参数估计的有效性和一致性［27］，并且保证了生物量估计的可加性，为建立海南木麻黄生物量估算模型提供了一种思路。当然，林龄不同，各器官的生物量分配也不同［28］。如果能按林龄分别建立生物量可加性模型最好［29-30］。但是，由于本研究样本量太少，不够分林龄进行研究。另外有学者认为生物量模型存在异方差性，对数转换或加权回归能有效地解决异方差现象，进而获得生物量无偏估计［23，31］。因此，在以后的研究中，采用不同林龄、不同立地、不同经营措施下的生物量数据，同时考虑生物量模型的异方差性，建立更为适用的木麻黄可加性生物量模型。

［1］刘宪钊，陆元昌，马履一，等.林场级森林林木碳储量估测方法研究［J］.北京林业大学学报，2013，35(5):144-148.

［2］Fang J Y，Wang Z M.Forest biomass estimation at regional and global levels，with special reference to China’s forest biomass［J］.Ecological Research，2001，16(3):587-592.

［3］Woodbury P B，Smith J E，Heath L S.Carbon Sequestration in the U.S.Forest Sector from 1990 to 2010［J］.Forest Ecology and Management，2007，241:14-27.

［4］Goicoa T，Militino A F，Ugarte M D.Modelling aboveground tree biomass while achieving the additivity property［J］.Environmental and Ecological Statistics，2011，18(2):367-384.

［5］李海奎，雷渊才.中国森林植被生物量和碳储量评估［M］.北京:中国林业出版社，2010.

［6］叶功富，林银森，吴寿德，等.木麻黄林生产力动态变化的研究［J］.防护林科技，1996(S1):17-20.

［7］黄义雄，方祖光，谢皎如，等.木麻黄防护林带生物量与生产力的研究［J］.福建师范大学学报:自然科学版，1996，12(1):113-118.

［8］洪元程，徐伟强，叶功富，等.东南沿海木麻黄人工林生物量估测模型研究［J］.浙江林业科技，2010，30(4):66-69.

［9］Parresol B R.Assessing tree and stand biomass:a review with examples and critical comparison［J］.Forest Science，1999，45(4):573-593.

［10］董利虎，李凤日，贾炜纬，等.含度量误差的黑龙江省主要树种生物量相容性模型［J］.应用生态学报，2011，22(10):2653-2661.

［11］曾伟生.立木生物量建模样本数据采集方法研究［J］.中南林业调查规划，2010，29(2):1-6.

［12］Monsi M.Mathematical models of plant communities∥Eckardt F E，ed.functioning of terrestrial ecosystems at the primary production level:Proceeding Copenhagen Symposium［R］.Paris:Unesco Press，1968:349-358.

［13］Fujimori T，Kawanabe S，Saito H，et al.Biomass and primary production in forests of three major vegetation zones of the Northwestern United States［J］.Journal of Japan Forest Society，1976，58(10):360-373.

［14］冯宗炜，陈楚莹，张家武，等.湖南会同地区马尾松林生物量的测定［J］.林业科学，1982，18(2):127-134.

［15］Bi H Q，Turner J，Lambert M J.Additive biomass equations for native eucalypt forest trees of temperate Australia［J］.Trees，2004，18(4):467-479.

［16］高惠璇，耿直，李贵斌，等.SAS系统-SAS/STAT软件使用手册［M］.北京:中国统计出版社，1997.

［17］Zhang X，Duan A，Zhang J.Tree biomass estimation of Chinese fir(Cunninghamia lanceolata)based on Bayesian method［J］.Plos One，2013，8(11):1-7.

［18］Paton D，Nuńez J，Bao D，et al.Forage biomass of 22 shrub species from Monfragüe Natural Park(SW Spain)assessed by loglog regression models［J］.Journal of Arid Environments，2002，52(2):223-231.

［19］曾慧卿，刘琪璟，冯宗炜，等.红壤丘陵区林下灌木生物量估算模型的建立及其应用［J］.应用生态学报，2007，18(10):2185-2190.

［20］Alaback P B.Biomass regression equations for under story plants in coastal Alaska:Effects of species and sampling design on estimates［J］.Northwest Science，1986，60:90-103.

［21］Ter-Mikaelian M T，Korzukhin M D.Biomass equations for sixtyfive North American tree species［J］.Forest Ecology and Management，1997，97(1):1-24.

［22］Wang C.Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests［J］.Forest Ecology and Management，2006，222(1/3):9-16.

［23］董利虎，李凤日，贾炜纬.东北林区天然白桦相容性生物量模型［J］.林业科学，2013，49(7):75-85.

［24］Cunia T，Briggs R D.Forcing additivity of biomass tables:some empirical results［J］.Canadian Journal of Forest Research，1984，14(3):376-384.

［25］Carvalho J P，Parresol B R.Additivity in tree biomass components of Pyrenean oak(Quercus pyrenaica Willd.)［J］.Forest E-cology and Management，2003，179(1):269-276.

［26］张雄清，雷渊才.基于定期调查数据的全林分年生长预测模型研究［J］.中南林业科技大学学报，2010，30(4):69-74.

［27］Rose Jr C E，Lynch T B.Estimating parameters for tree basal area growth with a system of equations and seemingly unrelated regressions［J］.Forest Ecology and Management，2001，148(1):51-61.

［28］李燕，张建国，段爱国，等.杉木人工林生物量估算模型的选择［J］.应用生态学报，2010，21(12):3036-3046.

［29］Balboa-Murias M Å，Rodríguez-Soalleiro R，Merino A，et al.Temporalvariations and distribution ofcarbon stocks in aboveground biomass of radiata pine and maritime pine pure stands under different silvicultural alternatives［J］.Forest Ecology and Management，2006，237(1/3):29-38.

［30］Zheng H，Ouyang Z Y，Xu W H，et al.Variation of carbon storage by different reforestation types in the hilly red soil region of southern China［J］.Forest Ecology and Management，2008，255(3/4):1113-1121.

［31］曾伟生，唐守正.非线性模型对数回归的偏差校正与加权回归的对比分析［J］.林业科学研究，2011，24(2):137-143.