70%低地板轻轨列车车内声学计算与分析
2015-06-28邱晓磊周劲松马敏纳
邱晓磊 周劲松 马敏纳 李 卓
(1.同济大学铁道与城市轨道交通研究院,201804,上海;2.北京汽车股份有限公司汽车研究院,101300,北京//第一作者,硕士研究生)
近年来,低地板轻轨车辆以造价低廉、无需专用路段、无需站台、上下客方便等优点受到国内专家的广泛关注[1]。由于低地板轻轨列车并不设专用线路,可以与其他地面车辆共用道路,所以对其产生的噪声有很高的限制要求。进行列车内噪声因素分析,对于改善旅客的乘车环境,提升低地板轻轨车辆的市场竞争力具有重要意义。
本文针对无内装结构的70%低地板轻轨车辆(头车)的声-固耦合系统[2]进行研究,运用动力学、有限元和声学仿真软件对车体进行噪声和结构分析,得到需要优化的块板件,为改善车体结构提供理论依据。
1 车体动力学分析
采用的整车车辆动力学模型如图1所示,为3模块编组,包含3 个转向架(2 动1 拖),以及车体、构架和轮对,车辆间通过铰接连接。假设车体、构架及轮对为刚性,车体间的铰接关系用弹簧来模拟。

图1 车体动力学模型
通过动力学仿真,模拟出该动力学模型车辆在美国六级轨道谱上运行时[3]二系悬挂与车体连接处的作用力和车体间连接的下铰力。可输出12 个二系悬挂处X、Y、Z 方向作用力的时域信号、6 个下铰处X、Y、Z 方向力的时域信号。
将所获得的时域信号进行频谱分析,截止频率为100 Hz。下绞处纵向力的幅频、相频曲线如图2、图3所示。

图2 下铰处纵向力幅频图

图3 下铰处纵向力相频图
2 车体结构模态及频率响应分析
2.1 车体有限元模型[4]
无内装70%低地板轻轨列车由车头、侧墙、端墙、车顶高地板、低地板等部分组成。在车身模型的二系悬挂连接处建立弹簧单元,刚度为一系和二系悬挂的串并联总刚度。根据车身实际约束和加载情况,将动力学分析所得的各作用力的频域幅值和相位作为激励,加载至相应位置。车体有限元模型及边界条件如图4所示。图中浅色三角形代表模型约束位置,深色三角形代表载荷加载位置。

图4 车体有限元模型及边界条件示意图
在车体有限元模型基础上,对车窗及车门用玻璃材料进行封堵,使车体内室封闭。运用此模型可模拟出车体在运行时的频率响应。封堵后的模型节点数为281 863,单元数为319 888。频率响应有限元模型如图5所示。
图5 频率响应有限元模型
2.2 结构模态分析
本文采用Lanczos 模态算法[5]对模态振型进行质量归一[6]。鉴于结构模态计算时高阶模态密集,表1 仅列出可能与声学模态产生耦合振动的模态频率值,其对应的模态振型如图6~图9所示。

表1 部分模态频率

图6 第12 阶模态

图7 第38 阶模态
2.3 频率响应分析
采用封堵后的有限元模型进行相应的约束和加载,对整车进行频率响应计算,输出节点位移。此步所得的车体振动信息可作为声学边界元激励,进行下一步的声学仿真。图10~图13 为部分频率响应下的位移云图。

图8 第47 阶模态
图9 第190 阶模态

图10 20.05 Hz 频率响应的位移云图

图11 32.05 Hz 频率响应的位移云图

图12 36.05 Hz 频率响应的位移云图

图13 72.05 Hz 频率响应的位移云图
3 车内噪声分析
3.1 声学模型建模
基于车体有限元模型,提取车体内表面网格,对未封闭处进行密闭,形成车体内室密闭空腔。针对该车体内室空腔网格形成的内室空间,采用实体单元进行网格划分,形成声学有限元网格。最后生成的车辆声学有限元模型包含315 635 个节点,298 334个单元,如图14所示。

图14 声学内室空腔有限元模型
3.2 声学模态分析
利用声学内室空腔有限元模型进行声学模态分析[7],模型边界不添加任何吸声或隔声材料。声学模态频率如表2所示。

表2 声学模态频率表
截取引起车体结构振动的频率与声学模态产生耦合,并且在车内形成稳定的声压分布、放大噪声、产生低频轰鸣感的频率值。图15~图17 为相应频率值下声学模态的声压云图。

图15 第2 阶声学模态的声压云图

图16 第3 阶和第4 阶声学模态的声压云图

图17 第8 阶和第13 阶声学模态的声压云图
3.3 车内噪声分析边界条件及场点布置
将2.3 节所得到的车体板件频率响应位移作为声学激励,不考虑轮轨噪声和气动噪声,车体内室空腔边界不做任何吸声处理。
因车体为对称结构,根据ISO 3381《各种有轨车辆噪声测量》和ISO 3095《铁道车辆噪声测量》标准,在车体的地板上方设置5 个离散的场点。各场点距离其地板高度为1.6 m,沿X 轴从负方向到正方向依次为 1、2、3、4、5号场点。表 3 为 ISO 标准场点编号及名称。图18 为ISO 标准场点的位置图。
3.4 车内ISO标准场点噪声结果分析
本次计算的车内噪声由车体壁板振动激发,所以在车体内室空腔边界处噪声较大。ISO 标准场点位于车体内室横断面中心处,相对噪声较小。各ISO 标准场点的总声压级列表见表4。5 个场点声压对比如图19所示。
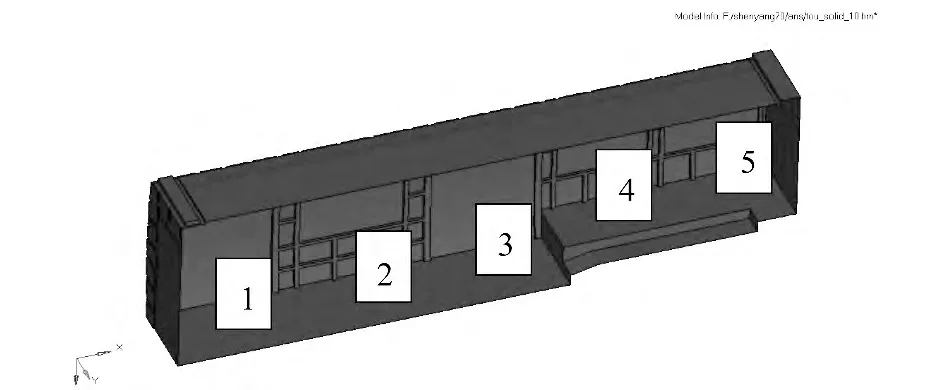
图18 ISO 标准场点的位置图
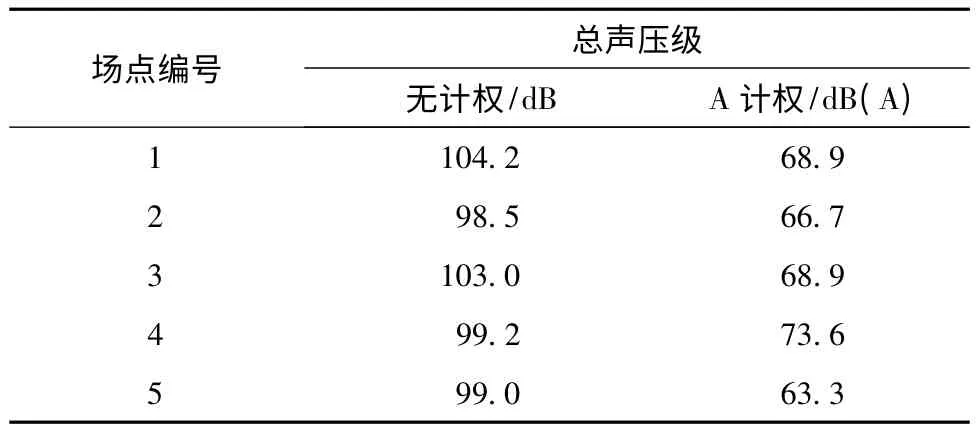
表4 各场点总声压级列表

图19 5 场点声压对比图
综合分析5 个ISO 场点的声压分布特点发现,场点声压较大峰值出现在 20.05 Hz、36.05 Hz、54.05 Hz、72.05 Hz、88.05 Hz。提取这 5 个频率作为板件贡献量计算的分析频率。由图2、表2 和图19 可知,激励力和车体声学振动在36 Hz 左右发生了耦合。
4 车体板件贡献量分析
4.1 车体板件分组
根据车体的各个功能部件,合并贡献量不明显的板件,车体板件大致可分为车顶、侧墙、端墙、低地板及高地板五类。表5 为板件编号与板件名列表。图20 为各组板件所在的位置,括号内为左侧对应板件位置。
4.2 车辆板件贡献量分析结果
车体呈长筒形,各板件振动所激发的噪声经过车体壁板的反射、折射,声压的幅值、方向及相位都有所不同。车体任意点的声压为所有板件辐射噪声的总和,这就造成有些板件辐射的噪声在该点贡献量为正,有些板件辐射的噪声在该点贡献量为负。在对车体的板件进行设计和优化时,必须针对贡献量为正的板件进行优化才能达到效果。如果针对贡献量较低的板件进行优化,反而可能增大噪声。基于以上原理分析板件在各峰值频率的贡献量,计算结果如图21~25所示。

表5 板件分组列表

图20 板件所在位置示意图
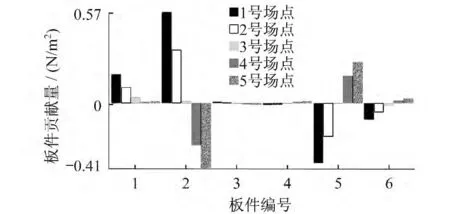
图21 20.05 Hz 时各场点板件贡献量柱状图
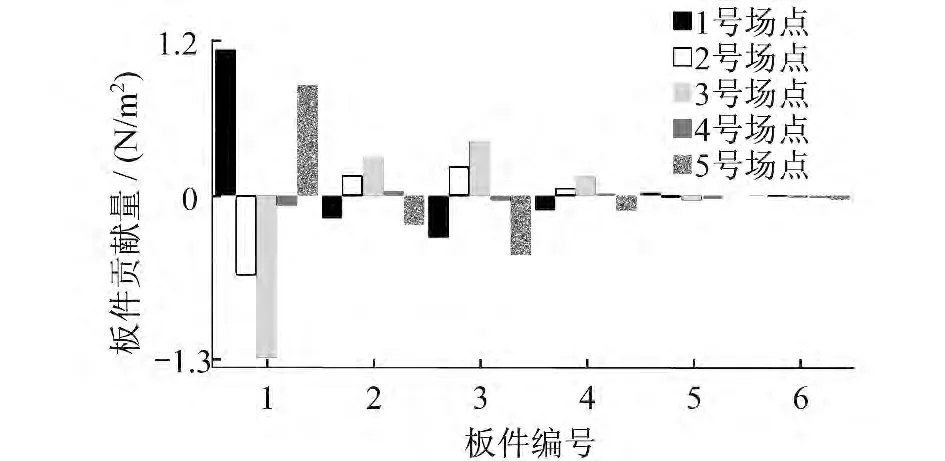
图22 36.05 Hz 时各场点板件贡献量柱状图

图23 54.05 Hz 时各场点板件贡献量柱状图
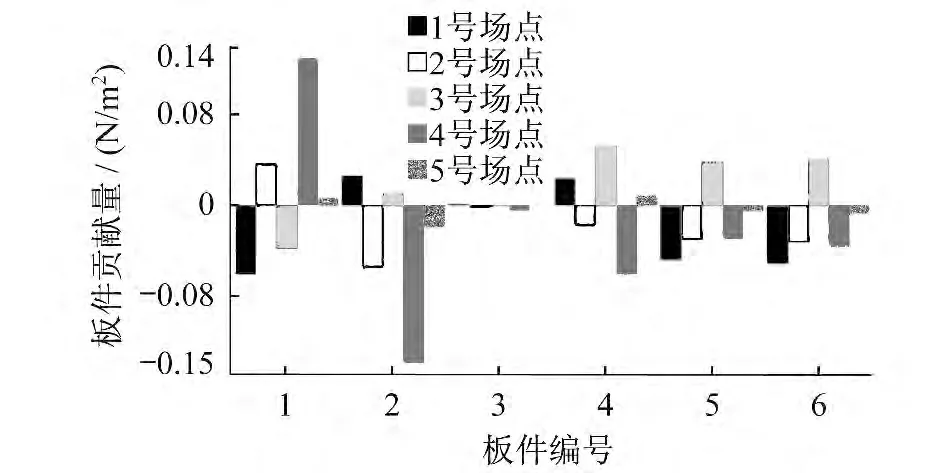
图24 72.05 Hz 时各场点板件贡献量柱状图

图25 88.05 Hz 时各场点板件贡献量柱状图
综合考虑各个频率下板件的贡献量正负值可以得出,1号板件在高声压频率下正贡献量相对较大,负贡献量综合最小。因此,可将车顶作为目标板件进行减振降噪优化。
5 结论
(1)根据车内ISO 标准场点噪声分析结果,可获得与声学模态产生耦合振动的模态频率值(见表1)。在设计车体下吊时,应使激励源远离这些车体结构模态频率,避免车体发生共振。
(2)车内某点声压在频域上分布极不均匀,普遍存在几个较大的峰值。该点的总声压级由这几个声压峰值决定。对车内噪声进行优化时可将声压峰值处的频率作为目标频率。
(3)为防止车体声腔发生共振,应使车体激励源远离车体声学模态频率。
(4)通过对比车体板件贡献量可知,需对车顶进行进一步的减振降噪优化。此为厂方进行结构优化和噪声控制提供了理论依据。
本文基于特定频率处板件声场贡献量、结构模态、声学模态计算结果对车体下吊设备频率的影响所提出的建议可供厂方参考,在今后试验中可以进一步得到验证并修正。
[1]钱小磊.70%低地板轻轨车车体强度分析与室内噪声预测[D].大连:大连交通大学,2011.
[2]马天飞,林逸,张建伟.车室声固耦合系统的模态分析[J].机械工程学报,2005,41(7):225.
[3]耿跃,胡用生.轨道车辆动力学性能仿真用轨道谱的研究[J].城市轨道交通研究,2010(7):20.
[4]李 卓,周劲松,张学铭,等.地铁车辆轴箱吊耳动态分析和优化[J].计算机辅助工程,2012,21(1):27.
[5]张静,刘明辉,郑钢铁.Lanczos-QR 方法在大型非比例阻尼结构复模态计算中的应用[J].振动与冲击,2011,30(5):222.
[6]林贤坤,覃伯英,张令弥,等.基于附加质量的试验模态振型质量归一化[J].振动、测试与诊断,2012,32(5):784.
[7]周鋐,金欢峰,靳晓雄.轿车车内空腔声学模态[J].同济大学学报:自然科学版,2001,29(5):557.
