CBTC 仿真测试中车辆运动学模型的应用

王洪涛

(中铁上海设计院集团合肥有限公司，230011，合肥∥工程师)

1 城市轨道交通牵引计算的研究背景

CBTC(基于通信的列车控制)系统是一个连续数据传输的自动控制系统，利用高精度的列车定位实现双向连续、大容量的车地通信。在上线应用前对整个系统进行仿真测试，对于缩短系统研发周期、提高系统的安全性和可靠性具有重要意义。

CBTC 仿真测试是在模拟城市轨道交通信号系统现场设备的运行环境和效果基础上，对城市轨道交通信号系统关键设备的功能进行测试。牵引计算是车辆动力学模型研究的核心，也是实现CBTC 系统验证测试的前提。通过牵引计算可以为列车运行控制系统提供精确的信标信息，还可以为其精确停车定位以及能耗控制提供试验基础。

牵引计算在仿真测试中的作用如图1所示。

图1 牵引计算与其他子系统关系图

我国已发布的《列车牵引计算规程》主要针对的是铁路机车的牵引计算，而对于城市轨道交通牵引计算的研究相对较少。城市轨道交通与铁路的运输方式和线路条件等多方面存在显著差异，由此决定了城市轨道交通车辆牵引计算不能照搬《列车牵引计算规程》，需要进行有针对性的研究。

本文将在文献［1］和文献［2］的基础上，做完整的牵引计算分析，探索如何为CBTC 仿真测试提供城市轨道交通车辆动力学模型，并结合实际线路数据对模型进行验证。

2 列车牵引计算数学模型

为了尽可能地发挥牵引能力和制动能力，本文选用最快速度策略［3］进行分析。根据最快速度策略，需遵循以下2 个原则:① 加速过程按照最大牵引力进行计算;② 停车制动过程可输出最大的制动力。

2.1 运动学模型

在建立列车牵引数学模型时，假设列车都是在做匀变速运动。整个牵引过程可以看作是有限次Δt 的牵引过程，故可以针对每个Δt 内的运动情况进行分析。

根据假设条件建立如下模型:

目标函数

式中:

t——运行时间;

ti——第 i 步的时间;

s——在整个运行过程中列车的运行距离;

si——ti时列车的运行距离;

vi——ti时列车的运行速度;

F——列车在运行过程中所受到的合力，kN;

G——包括了回转质量［1］的整个列车总质量，kg。

式(3)中的合力和质量可以通过下文的分析得到，这样就可以通过迭代获得整个列车的运动状况模拟数据。列车在行驶过程中受力变化很复杂，要建立运动学模型首先要进行列车的受力分析。

2.2 牵引计算

对于城市轨道交通列车而言，由于其编组车辆少、列车长度较短，因此，在运行过程中会受到大小和方向不同的各种力的作用。但在牵引计算的力学模型中只考虑与列车运行速度有关牵引力、阻力和制动力。

2.2.1 牵引力

车辆所受合力由牵引力FT和阻力W 一同构成，计算公式为:

车辆牵引力的大小是根据牵引电机的牵引特性曲线(牵引力-速度)来给出的。在已知速度的情况下，可以利用拉格朗日插值法从电机牵引特性曲线上拟合得出所需要的牵引力公式。

从牵引特性曲线中读出关于速度-牵引力关系的数据对(设有n+1 对)，任意两个vj都互不相同，那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:

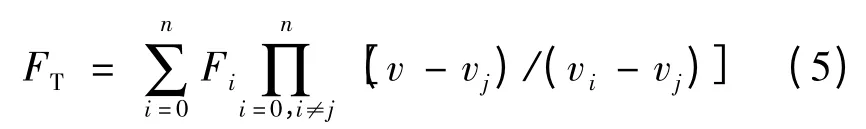
2.2.2 阻力

车辆运行区间阻力W 由基本阻力W0和附加阻力Wa组成。Wa包括坡度附加阻力Wi、曲线附加阻力Wr、隧道附加阻力Ws以及附加起动阻力 Wqz，通常分别以单位力 w0、wa、wi、wr、ws、wqz的 形 式表示。

在实际运行中，列车一旦起动，列车阻力就从起动阻力回落到基本阻力，是一个从静态到动态的瞬变过程。在本牵引仿真计算中，假设从起动开始到列车速度为5 km/h 的时间内起动阻力有效，区间阻力如下。

当 v ＜ 5 km/h 时:

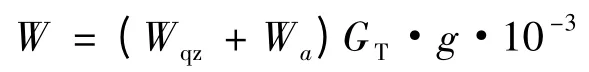
当 v ≥ 5 km/h 时:

式中:

GT——列车静态总质量;

g——重力加速度。

单位附加阻力wa主要包括坡道附加阻力、曲线附加阻力和隧道附加空气阻力，即:

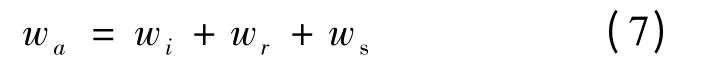
由于列车起动比较频繁，根据计算精度以及经验取值，单位起动阻力可以按照wqz=5 N/kN 进行计算。

由于影响基本阻力的因素极为复杂，在使用中通常按照由大量试验综合得出的经验公式进行计算。这些公式一般都采用单位基本阻力的形式表达，都是列车运行速度v 的二次函数形式:

列车在坡道上运行时，还受到重力沿轨道方向的分力的影响，这个分力就是坡道附加阻力。运用斜坡上的物体受力分析可以得出单位坡道附加阻力:

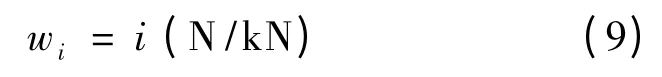
i 为坡度千分数，上坡时为正值，下坡时为负值。

列车进入曲线运行时，因部分轮缘压向外轨头而产生的横向滑动以及转向架中心盘等处的摩擦力称为曲线附加阻力。它的大小与诸多因素有关，因此很难用理论方法推导，一般采用综合经验公式计算单位曲线阻力:

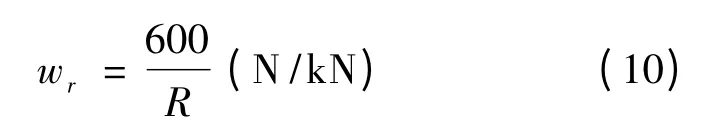
其中，R 为曲线半径，单位m。

ws为单位隧道附加阻力，它由试验确定。一般情况下，列车在隧道中行驶时，气动阻力比在地面线路上要高出l 倍以上，所以隧道附加阻力不可忽视。当车辆在隧道内部运行时，可以假设隧道附加阻力为起动阻力或基本阻力的整数倍。

最后，式(3)中提及的包括了回转质量在内的车辆总质量的计算公式［1］如下:

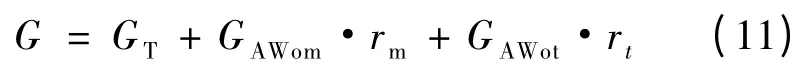
式中:

GAWom——动车静态质量，kg;

GAWot——拖车静态质量，kg;

rm——动车回转质量系数，一般取0.1;

rt——拖车回转质量系数，一般取 0.05。

2.2.3 制动力

制动情况下的合力由制动力FB和阻力w 组成，公式为:

车辆有空气制动与机械制动2 种方式互为补偿，在任何速度下都能通过两者的作用给出最大制动力性能，因此可以假设制动力FB保持恒定，且由车辆特性获得。

综上，通过对列车牵引原理以及列车运行过程中的受力情况的分析，为建立仿真模型提供了理论基础，从而得出了可以用于CBTC 仿真测试的车辆运动学仿真模型。

3 牵引电算

用计算机进行的城市轨道交通牵引仿真计算，通常简称为牵引电算。牵引电算是以车辆动力学模型为基础，结合具体线路的平纵断面和具体车辆的牵引特性，计算列车运行过程中的速度、加速度以及运行距离等。

牵引电算软件算法实现的简要流程如下:

(1)根据配置数据查询当前位置的坡度和曲率，计算坡度附加阻力与曲线附加阻力;

(2)计算起动阻力和基本阻力，进而计算隧道附加阻力;

(3)通过式(6)计算总阻力;

(4)列车运行时，无论是牵引还是制动，都可以根据牵引或制动的输出控制量占全量程的比例关系计算得到此时实际输出的牵引力或者制动力大小，进而可以计算合力。

(5)最后，通过运动学模型式(1)、(2)、(3)来计算列车的速度和总位移。

进行牵引电算需要大量的基础数据，所需的数据类型主要分为以下几类:①线路数据，包括线路长度、坡度、曲线半径以及隧道区间信息;② 车辆编组方式，动车质量、拖车质量以及载客量等;③ 列车基本阻力特性数据;④电机的牵引力-速度关系曲线与制动力-速度关系曲线。

通过比较列车运行控制系统在现场环境和仿真环境中的运行数据，可验证模型的正确性。

4 实例验算

4.1 数据准备

本文以北京地铁亦庄线为例进行实例验算。亦庄火车站是亦庄线的终点站，属于地下站;列车采用3 动3 拖6 节车编组方式。

表1 给出了实例所选取的路况及车辆信息。

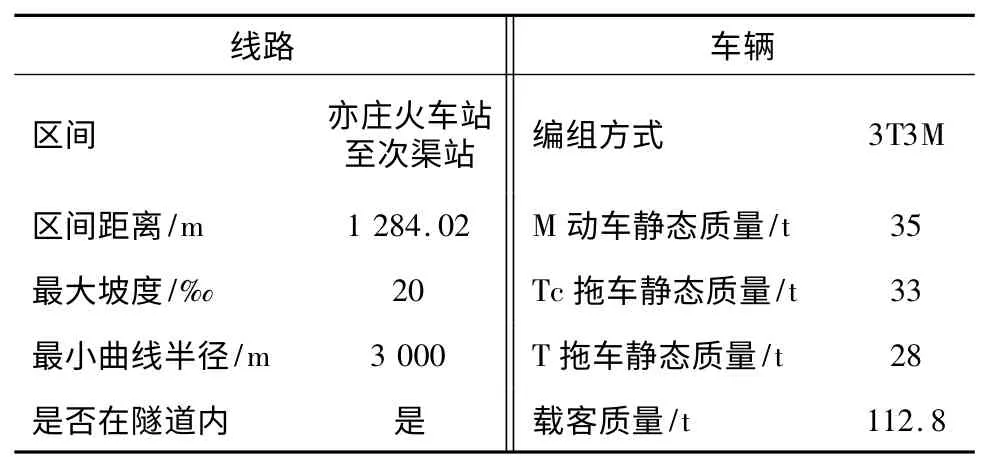
表1 实例主要工况信息

基本阻力特性以及牵引力-速度关系可以根据车辆提供的特性曲线，利用拉格朗日插值方法得到如下的2 次插值多项式，单位是kN。

当 5 km/h ＜ v ≤ 80 km/h 时:

当 0 ≤ v ＜ 36 km/h 时:

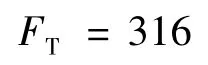
当36 km/h ≤ v ＜ 46 km/h 时:

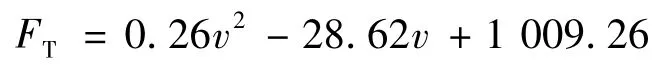
当 46 km/h ≤ v ＜ 80 km/h 时:

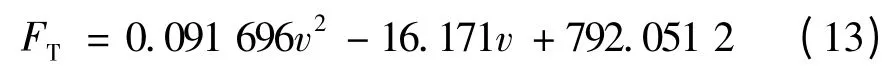
根据车辆特性，假设制动力保持恒定值如下。

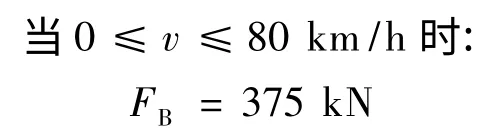
4.2 结果分析和比较

表2 中给出的现场运行特性是在现场列车运行控制系统控制下得到的运行数据;模拟运行特性是在仿真测试平台下，利用相同的设备进行控制，使用基于模型的牵引电算软件得出。两者比较结果如表2所示。

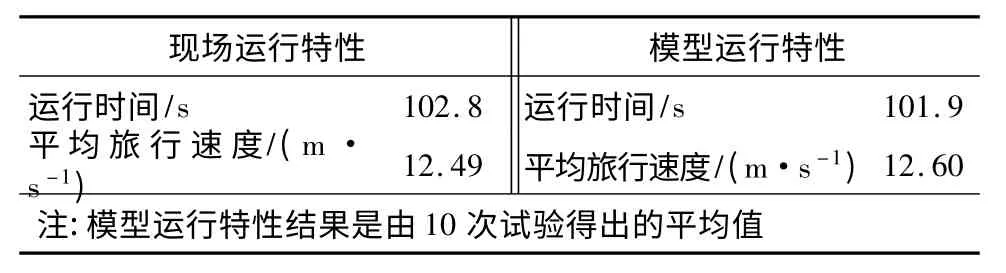
表2 运行特性数据对比

通过对比发现，在仿真测试下得到的运行时间与实际的运行时间几乎相同，如此小的误差，说明了模型与实际车辆动力特性的吻合度非常高。由此也可以证明，此模型可以满足仿真测试对于牵引计算的需要。

5 结语

结合CBTC 仿真测试的需要，在对城市轨道交通列车牵引计算进行的受力分析的基础上建立了力学模型，设计了牵引算法。用软件实现了本文所设计的模型，并将该软件在仿真测试中与实际线路中的运行效果进行对比，最终验证了模型的正确性。

［1］谢宏诚.城市轨道车辆牵引仿真研究［D］.上海:同济大学，2006.

［2］谢小淞.城市轨道交通列车牵引计算系统的研究［J］.交通标准化，2005(9):22.

［3］石红国，彭棋渊.城市轨道交通牵引计算算法［J］.交通运输工程学报.2004(9):30.

［4］王武生，詹振炎.基于Visual C+ +6.0 平台的列车牵引计算系统的开发［J］.交通与计算机.2003(5):104.