一种新的粒子群拓扑设计准则
2015-06-27马胜蓝叶东毅杨玲玲
马胜蓝,叶东毅,杨玲玲
(1.福建省农村信用社联合社科技服务中心,福州350001;2.福州大学数学与计算机科学学院,福州350108)
一种新的粒子群拓扑设计准则
马胜蓝1,叶东毅2,杨玲玲2
(1.福建省农村信用社联合社科技服务中心,福州350001;2.福州大学数学与计算机科学学院,福州350108)
粒子群优化算法的搜索性能取决于算法探索和开发能力的平衡,与算法所使用的拓扑结构相关。现有的粒子群拓扑结构不能较好地平衡算法的探索性能和开发能力。为此,依据低配位数、高堆积密度和3D结构等特征,提出一种新的拓扑设计准则。根据此准则,设计一种菱形十二面体的拓扑结构,该拓扑结构由球体按照六方晶格和面心立方结构堆积而成,是具有最大空间利用率的3D最密堆积结构,且拥有较低的平均配位数。实验结果表明,与现有的拓扑结构相比,该拓扑结构搜索到全局最优值的概率较高。
粒子群优化算法;设计准则;配位数;菱形十二面体;密堆积;3D结构
1 概述
粒子群优化(Particle Swarm Optimization,PSO)算法是由E-berhart和Kenney发明的一种全局优化进化算法[1-2],作为一种重要的群智能算法,国内外对此作了大量的研究工作。文献[3]提出结合长期记忆禁忌搜索方法的粒子群并行子群优化算法,文献[4]将粒子群算法映射到博弈环境。
然而如何合理地利用自身经验信息和群体共享信息的问题一直未能有效解决。而Kenney研究出粒子群每个个体不应该简单地被邻居中的最优值所影响,因此,提出基于所有邻居信息值的全息粒子群算法[5]。本文研究就是在此基础下展开的。全息粒子群(Fully Informed Particle Swarm,FIP)可以看作一种深层次的社会网络粒子群优化算法,该优化算法所利用的信息均来自于粒子的邻域[6],并且提出了许多拓扑(例如All、Ring、Four clusters、Pyramid和Square),其中,冯诺依曼结构即Square拓扑由于其较好的搜索能力而被推荐使用。为了增强全息粒子群算法的搜索能力,国内也有部分学者对此做改进,如文献[7]利用带增强策略的全息粒子群算法用于解决属性约简问题。
根据晶体学的知识,提出一种新准则,它所设计出的拓扑结构具有令人满意的通信能力。在此准则下,PSO的探索能力和开发能力被粒子之间的化学键能E所影响。一般的,堆积密度和配位数可以直观地反应出晶体的键能,而相应的键能决定着特定的堆积密度和配位数,最终将会决定一个拓扑的结构。因此,从晶体学概念映射到拓扑结构中,堆积密度决定着粒子群在拓扑结构内部搜索到全局最优值的概率,即影响着开发能力;而配位数反应出需要多少个粒子去打破化学键才能探索到新的区域。本文设计的一个具有适当键能(即低的配位数、高堆积密度和3D结构)的拓扑,可以保证好的通信能力。对于Square拓扑,在本文提出的设计准则评估下,拓扑仅是一个按照网格规则堆积的平面2D点阵,并不满足最密堆积。而当群体飞向一个局部最优解,且全局最优解在该局部最优解的相反位置时,粒子群体由于仅为2D结构,很难搜索到全局最优解。综上所述,一个适当设计的拓扑结构应该能够平衡PSO的探索和开发能力。
根据提出的设计规则,本文设计出一种新的粒子群拓扑结构。该拓扑结构称为菱形十二面体,它通过将球体按照六方晶格和面心立方结构堆积而成,具有3D最密堆积和较低的平均配位数等特点。
2 新的拓扑设计准则
粒子群优化算法的搜索过程实质上就是社会群体交流信息的过程。为了构建一个更紧凑的信息交流,前人在PSO中引入了一种社会网络拓扑(如图1所示),并构建出一种全息粒子群[5]。这些拓扑极大地改进了PSO的搜索能力并影响着群体的通信能力。但是当前的研究并没有提出一个令人满意的拓扑设计准则。

图1 Square,All和Ring拓扑
本文根据晶体学中的键能概念,提出一种新的设计准则。假设粒子群飞行在搜索空间中,粒子之间交流的信息被粒子间连接的化学键所影响,则键能决定着拓扑的结构和对应的特征。因此,在晶体学观点中,键能是粒子群优化算法的探索和开发能力的决定性因素。虽然不能直接简单地计算出键能,但是配位数和堆积度可以间接地反映出键能的强度。其中,配位数常用来决定需要多少能量来打破键能,以此决定着探索能力;堆积密度影响着开发能力,进而影响着粒子在局部区域的搜索效率。此外,粒子群的适应值还可以看作需要打破键或者重构键的外部能量。虽然拓扑结构是逻辑关系,并不是空间关系,但是空间紧致性可以反映出粒子的趋向性。
2.1 配位数
在离子晶体中,晶格能表示离子之间的键能强度:越大的晶格能将具有更稳定的离子晶体。信息在离子之间传递被离子键所影响。离子键的本质是正负离子之间的静电力。如果2个离子可以看作球体的话,那么根据库仑定律就可以得出如下结论:离子电荷越高,两核间距越小,静电作用越强,离子键越强,离子晶体就越稳定。
已知配位数是一个可以反应该键能的重要参数,常指化合物中心原子周围的配位原子个数[8-10]。正负离子半径比影响着配位数,进而影响化学晶体结构的稳定性[11]。当r+/r->0.414(r为正负离子的核间距离),配位数将大于4,形成稳定晶体;当r+/r-<0.414,配位数为4,晶体正好处于一个非稳定的结构。随着r+持续的变大,配位数可以达到12个,相反的,随着r+减小,配位数可以为3。
2.2 球体堆积和最密堆积
在几何上,球体堆积指非重叠球体在一个封闭空间内的堆积。这些球体具有相同大小的尺寸,利用该特性可以将堆叠的球体看作粒子群中的粒子。密堆积是相同大小球体的紧密排列,其中,已知的最密堆积方式为六方密堆积和立方密堆积[12]。立方密堆积(也称为面心立方[13])按照ABCABC…规律重复堆积;而六方密堆积[14]是按照ABABAB…顺序堆积。因为滑动一列粒子的位置并不会影响这些球体的体积,所以这2种堆积方式的密堆积度都等于。图2显示了面心立方(Face-Centered Cubic,FCC)的单位晶格,该晶格包含8个1/8的球体和6个半球体。图3是六方密堆积(Hexagonal Close Packing,HCP)结构的单位晶格,该晶格中,顶层和底层分别包括6个1/6球体和一个半球体,中间层包含3个球体。

图2 FCC单位晶格

图3 HCP单位晶格
2.3 设计准则描述
综上分析,可以得出一种新的可以保证通信能力的拓扑设计准则:拓扑应该具备适当的键能,拥有较低的配位数,高的堆积密度和3D结构。该准则详细的叙述如下:
(1)配位数
粒子邻域的配位数越低,则该粒子可以更灵活地打破连接的化学键,从而搜索到新的空间;过低的配位数则会使整个晶体结构松散。如2.1节所述,配位数为4时正好使晶体从稳定状态转化为不稳定状态,而且通过Mendes的实验[5]也可以发现此个数下粒子群拥有较好的探索能力。根据离子晶体的知识可以近似确定一个好的拓扑配位数应该接近于4。该数值越小将会使得晶体脆弱,而越大将会导致晶体缺乏弹性。
(2)堆积密度
这里的空间堆积紧密性间接反映出粒子群搜索的趋向性,虽然粒子群在搜索过程中,是根据自身局部领域的逻辑结构信息,但是粒子的自身搜索却是一个局部区域搜索,走向将会趋向于空间结构,最终收敛于局部最优解。因为粒子之间的领域关系,正好也是粒子群将会聚集学习的方向,从空间角度上考虑也可以解释粒子群会逐渐飞向局部最优解中,所以本文在粒子群拓扑结构的逻辑结构上,也考虑了空间上的趋向性,对于逻辑拓扑上的空间特性也要求了堆积密度。先考虑2D空间内全局最优解正好处于拓扑内的情况,图4显示了2种不同的拓扑,其全局最优解(黑点)正好处于对应的拓扑内。每个球体的面积可以看成粒子的可视距离,粒子在自身的可视距离内能够直接找到全局最优解。则密堆积度就可以用于表示拓扑范围内能搜索到最优解的概率,所以,图4(b)找到最优解的概率更高。
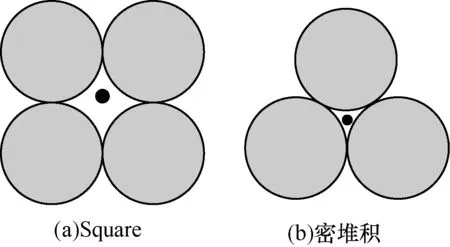
图4 2D空间内粒子飞向拓扑内部全局最优解示意图
类似的,在3D空间内密堆积也可以表示为找到全局最优解的概率,所以更高的密堆积度具有更强的本地开发能力。
接下来考虑粒子飞向局部最优解区域,而全局最优解正好处于相反位置的情形。如图5所示的2D拓扑结构,当整个拓扑趋向于上半部区域时,下部的区域对整个粒子群体而言是块盲区。而相反的,粒子群体若具有3D拓扑结构(图6),它可以通过打破下平面的键,从而吸引整个拓扑朝向新的区域,因此,仍然有机会探索到全局最优值所在的空间。

图5 2D结构的粒子飞向局部最优解示意图

图6 3D结构的粒子飞向局部最优解示意图
综上所述,一个适当的键能体现为较低的配位数,高堆积密度和3D结构,可以使得拓扑拥有更好的通信能力。由此构建的拓扑,还常影响着打破键的时机。
3 菱形十二面体及特性
为了验证提出的准则,本文根据此准则设计出一种新的拓扑,并验证该新的拓扑的搜索能力。
根据该准则设计一个拓扑,一般首选采用3D最密堆积结构。若将球体按照六方晶格和面心立方体结构堆积,中心球体与周围的12个同等大小球体相切,这样构成的结构可以为3D最密堆积结构。如果仅简单地连接这些球心而构成拓扑,将严重地违反低配位数这条特征。根据“Kissing number problem”[15],这种排列将会拥有最高的配位数12。因此,本文将中心球体与周围的球体相切的切面构成一个新的拓扑,该拓扑称为菱形十二面体[16]。它包括12个全等的菱形、24条边及14个顶点。图7显示了由14个顶点12个菱形所构成的菱形十二面体结构。由于长对角线是短对角线的倍,因此菱形的锐角大小大约为70.53°。这种堆积拓扑满足3D最密堆积,且具有堆积度74.05%,可以充分利用空间以达到最大的空间利用率。菱形十二面体的平均配位数仅为3.43,接近于准则设计的配位数标准4,所以,该拓扑在很大程度上满足设计准则。

图7 菱形十二面体
4 菱形十二面体与其他拓扑的比较
本节主要比较菱形十二面体与其他的拓扑的特征。
Square拓扑是通过将球体按照网格方式排列而形成的,仅是平面点阵和2D堆积。因为2D最密堆积是由一个球体周围围绕着6个球体(六方点阵)方式堆积而成,所以Square并不满足2D最密堆积。图8显示出Square拓扑的正方晶格。

图8 正方晶格
该晶格包括4个1/4的圆,则晶格内圆面积为As=πr2;正方晶格的面积为:Au=4r2;则堆积密度为η=π/4=0.785 4。
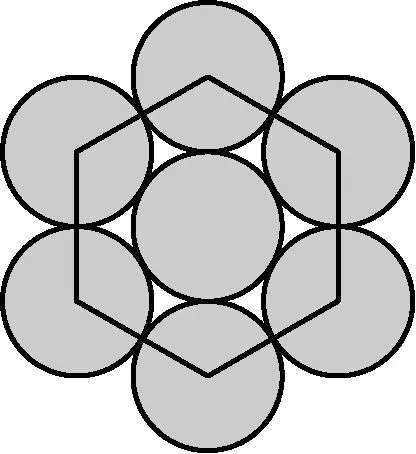
图9 六方晶格
从上述结果可以看出,在2D空间内,Square的堆积密度低于菱形十二面体的堆积密度,而在3D空间内Square搜索到拓扑内的全局最优点的概率未知。也就是说,菱形十二面体的开发能力比Square可信。然而Square的整体堆积密度0.785 4高于菱形十二面体的0.740 5,使得Square仍然具有较高的搜索能力,但2D结构限制了Square的通信能力,因此,具备3D结构的菱形十二面体开发能力强于Square。
这里将讨论另一种情形,即当全局最优解处于拓扑外的情况。拓扑处理该情况的能力可以间接反映出设计准则的有效性,因为适当的键能可以决定粒子打破键能而搜索到新的空间的时机。图10显示了全局最优解在菱形十二面体的菱形面外的情形(灰点表示原子;白点表示粒子)。其中,2个球体之间的连线是这2个原子的键,如果一个粒子倾向于飞向全局最优区域,它将在2轮迭代中传输自己的信息给菱形上的另外3个粒子,然后该菱形上的粒子一起决定是否要打破该键,所以最终打破键的能量将由这4个粒子来决定。一旦该键被打破,这个新的信息将会通过中间球体传播到剩余的11个原子。通过这种方式,整个拓扑将会逐渐地移向新的空间区域。可以说菱形十二面体拥有菱形搜索的特征,它需要4个决策粒子和2轮信息传播延迟去打破一个原子键来探索到新的区间。从本质上看该结构的搜索速度有点缓慢,却可以有效地搜索本地区域。

图10 3D空间菱形十二面体粒子飞向全局最优解示意图
在Square拓扑中,每个粒子完全等价于原子。当一个粒子倾向于飞向全局最优解时,它必须首先在一轮迭代中通知它的4个邻域,如图11,白点表示原子或者粒子。之后该粒子与邻域一起打破键,从而探索到新的空间。所以,Square需要5个决策粒子和1轮信息传播延迟去打破4个原子键来探索新的空间。该拓扑具有足够的决策粒子,并能够较快地探索到新的空间,但是打破过多的键导致了拓扑结构的不稳定。

图11 Square的粒子飞向全局最优解示意图
此外,All拓扑中每个粒子需要N个决策粒子打破N个键去探索新的空间,导致了该拓扑很难探索到新的空间。Ring拓扑仅需要2个决策粒子去打破2个键,这种过度简易的打破键的方式导致群体开发能力变弱。
综上所述,适当的键能会影响着PSO的通信能力,而且菱形十二面体比Square拥有更适当的键能,这间接加强了本文提出的设计准则的可信度。为了验证该结论,本文通过大量的优化问题来比较Square拓扑和菱形十二面体拓扑,如图12和图13所示。首先根据粒子的个数定义出2类拓扑,即简单和复杂拓扑,其中,带有16个粒子的Square拓扑(16-Square)、带有20个粒子的Square拓扑(20-Square)和简单菱形十二面体(Rhombic Dodecahedron)为简单拓扑;带有24个粒子的Square拓扑(24-Square)和2-菱形十二面体(由2个菱形十二面体拼接而成)为复杂拓扑。

图12 Square类拓扑

图13 菱形十二面体和2-菱形十二面体
最后,采用Mendes实验中所用的3个通信能力评价标准来评估如上拓扑。该评价标准采用3个参数来评估拓扑的搜索能力,表1列出了拓扑的3个统计量(平均距离、半径及分布序列),其中,第1个参数表示信息广播到整个拓扑需要的平均迭代次数;第2个参数表示最大迭代次数;第3个参数可以衡量信息通过拓扑传播的延迟情况的分布序列。注意的是分布序列的第1个数值表示的是图的平均度,也可以用于表示平均配位数。

表1 拓扑图统计量
以菱形十二面体为例计算如上参数,首先采用Floy-Warshall算法[17]计算出等权重拓扑的最短路径,通过这些最短路径,任意两点间的平均距离和半径都可以算出。菱形十二面体的最大传播距离为4,则该拓扑的半径为4。如第3节中所示,菱形十二面体拥有2类顶点,则拥有2类分布序列。在该拓扑中,有8个顶点拥有序列<4,4,4,1>,6个顶点拥有序列<3,6,3,1>,所以,最终的分布序列为<3.43,5.14,3.43,1>。
从表1可以看出,菱形十二面体类的拓扑,顶点直接可以传输到节点的个数低于Square类的拓扑,但是中间的传输过程可以影响更多的邻域。这就使得菱形十二面体搜索速度会有点缓慢,但是它具备足够的决策粒子去打破关键键,从而能够探索到新的空间。虽然这会导致较长的搜索时间,但是可以避免粒子扩散。该分析同时也证实了菱形十二面体的特性。
5 实验结果与分析
正如文献[5-6]研究中所描述的,粒子自身的索引可以从邻域列表中去除,并且没有任何社会心理学原则说明个体的经验在一定程度上有助于自身的学习。因此,接下去的实验中将主要讨论自身索引从邻域列表中去除的情况。实验包括2个部分:第1个部分利用Mendes的3个评价变量和5种算法模式来测试拓扑结构;第2部分利用更多的优化函数来比较Square和菱形十二面体拓扑结构。
5.1 3个独立变量的实验结果
本节使用3个独立变量来测试特定PSO拓扑的性能。第1个独立变量是标准化的性能,它通过分别归一化每个测试函数结果来找到一个最小的平均值,并且关注在较小的迭代次数内的结果;第2个独立变量是达到一个准据的平均迭代个数,表示着搜索速度;第3个独立变量为测试成功概率,即达到准据的概率。采用文献[5]给出的测试函数、准据和定义的9种不同更新粒子群经验值的粒子群算法。表2~表4展示了3个变量的测试结果,其中,加粗表示算法采用该种拓扑具有最好的结果;∞表示在10 000次迭代循环中无法达到准据。

表2 标准化性能比较

表3 达到准据的平均迭代次数

表4 达到准据的概率 %
从表2可以看出,当利用 FIPS、Self、wSelf、Canonasym和wFIPSasym算法时,菱形十二面体表现出很好的性能,这说明菱形十二面体能够快速地求出适应值峰值。另外可以看出,由于简单拓扑结构较小,与复杂拓扑相比,因此它可以较快地找到适应值峰值。
从表3可以看出,Square类的拓扑比菱形十二面体拓扑搜索速度快,由于菱形十二面体需要搜索多一维的空间,因此其搜索速度会稍微偏慢。但考虑第3个参数的测试结果,菱形十二面体在有限的时间内仍可以搜索到极优值。
从表4可以看出,2-菱形十二面体具有最高的概率找到全局最优解。由于菱形十二面体类的模型具有较强的搜索能力,它可以较好地解决那些复杂的非对称搜索任务。
5.2 优化能力比较
本节将给出更详细的比较,测试的函数细节可以在文献[18]得到,并且按序测试,实验过程利用40次计算的平均值。
在简单拓扑中,原始粒子群、基于20-Square和16-Square的粒子群这3个算法相比较,基于菱形十二面体的粒子群算法在标号1,2,6,16,17,18和19的基准函数上具有较低的平均值。单独比较菱形十二面体与16-Square,菱形十二面体拓扑在函数1~函数 6、函数 8~函数 13、函数 15~函数 19和函数21~函数22上生成了更接近于最优解的结果。在复杂拓扑中,2-菱形十二面体在大多数函数上比24-Square找到更优的结果。
图14和图15显示出性能结果比较,纵坐标表示归一化的数值结果,在归一化条件下,越低值则意味着更优的性能,越接近于最优解。
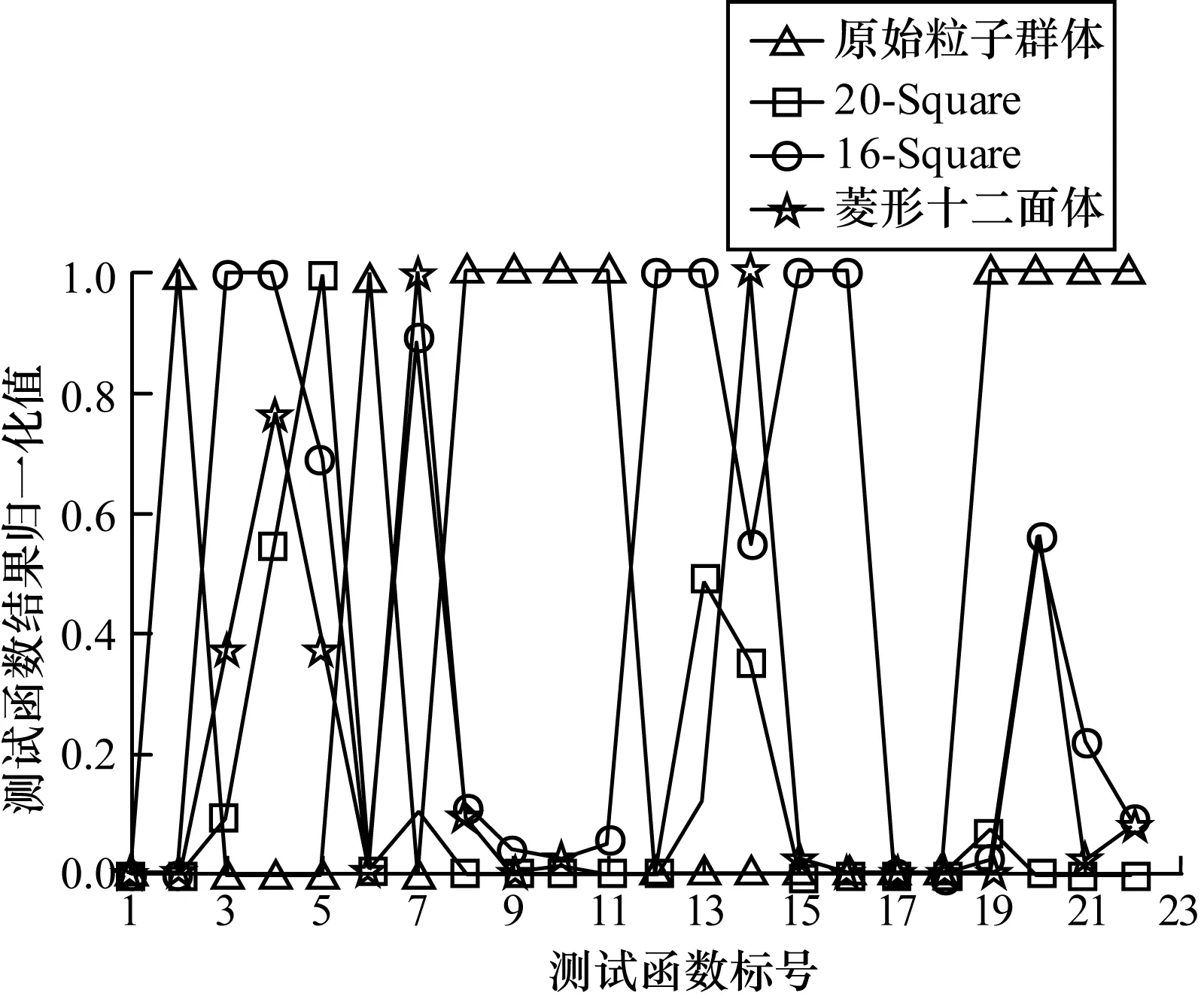
图14 简单拓扑性能比较

图15 复杂拓扑性能比较
从图14可以看出,基于菱形十二面体的粒子群算法在函数7和函数14上虽然拥有最高的值,但是实际的结果已经非常接近于最优解。另外可以看出,基于20-Square拓扑的粒子群优化算法处于最低的线,这点较好地说明粒子的个数对搜索能力有较大的影响。然而,仅比较16-Square和菱形十二面体,后一个拓扑的曲线显然低于前一个拓扑的曲线;虽然Square-16的粒子个数大于菱形十二面体,但是搜索能力显著低于菱形十二面体。
在图15中,2-菱形十二面体仅在函数3、函数14和函数20上搜索结果略差于Square-24,在其他函数上都优于Square-24并且非常接近于最优解。
综上所述,菱形十二面体具有很强的搜索能力,并且可以很快地达到适应值峰值,与现有的拓扑结构相比,该拓扑结构搜索到全局最优值的概率较高。如果粒子群的个数对于求解任务来说不是主要的影响因素,且搜索任务重点在于粒子的搜索能力,那么菱形十二面体拓扑是个首选。若粒子的个数也成为关键因素,2-菱形十二面体拓扑是更好的选择。
6 结束语
本文将键能的3个特征(低配位数、高堆积密度和3D结构)用于评价粒子群的探索和开发能力,为了能够有效地开发局部搜索空间和适时地探索到新的区域,提出一种新的PSO拓扑结构——菱形十二面体,该拓扑结构满足3D最密堆积结构,且具有较低的平均配位数,使其比之前研究推荐的Square拓扑具有更优的搜索能力。实验结果表明,基于菱形十二面体的粒子群优化算法能够更好地找到适应值峰值和全局最优值,具有较高的概率搜索到全局最优解。虽然菱形十二面体搜索速度稍微缓慢,但是在限定时间内仍然具有最高的解决优化问题的概率。今后将进行拓扑搜索速度的优化,以提高基于菱形十二面体的粒子群优化算法的处理速度。
[1] Kennedy J,Eberhart R C.Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Networks.[S.l.]:IEEE Press,1995:1942-1948.
[2] Shi Y,EberhartR C.A Modified ParticleSwarm Optimizer[C]//Proceedings of IEEE International Conference of Evolutionary Computation.[S.l.]:IEEE Press,1998:69-73.
[3] 马胜蓝,叶东毅.一种带禁忌搜索的粒子并行子群最小约简算法[J].智能系统学报,2011,6(2):132-141.
[4] 马胜蓝,叶东毅.一种基于博弈策略的群智能属性约简算法[J].计算机工程与应用,2012,48(1):145-149.
[5] Mendes R,Kennedy J.The Fully Informed Particle Swarm:Simpler,Maybe Better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210.
[6] Kennedy J.Small Worlds and Mega-minds:Effects of Neighborhood Topology on Particle Swarm Performance[C]//Proceedings of Congress on Evolutionary Computation.Washington D.C.,USA:IEEE Computer Society,1999:1931-1938.
[7] 马胜蓝,叶东毅.信息熵最小约简问题的若干随机优化算法研究[J].模式识别与人工智能,2012,25(1): 96-104.
[8] De A K.A Text Book of Inorganic Chemistry[M].[S.l.]: New Age International Publishers,2003.
[9] Hermann A,Matthias L,Peter S.The Search for the Species with the Highest Coordination Number[J]. Angewandte Chemie International Edition,2007, 46(14):2444-2447.
[10] McNaught A,Wilkinson A.Compendium of Chemical Terminology[M].[S.l.]:Wiley-Blackwell,1997.
[11] Pauling L.The Principles Determining the Structure of Complex Ionic Crystals[J].Journal of the American Chemical Society,1929,51(4):1010-1026.
[12] Hales T C.A Proof of the Kepler Conjecture[J].Annals of Mathematics,2005,162(3):1065-1185.
[13] Weisstein E W.Cubic Close Packing[EB/OL].(2011-08-21). http://mathworld.wolfram.com/CubicClosePacking.html.
[14] Weisstein E W.HexagonalClosePacking[EB/OL]. (2011-08-15).http://mathworld.wolfram.com/Hexagonal ClosePacking.html.
[15] Conway J H,Sloane N J A.Sphere Packings,Lattices,and Groups[M].New York,USA:Springer-Verlag,1993.
[16] Williams R.The Geometrical Foundation of Natural Structure:A Source Book of Design[M].New York, USA:Dover Publications,1979.
[17] Floyd R W.Algorithm 97:ShortestPath[J].Communications of the ACM,1962,5(6):344-345.
[18] Yao Xin,Liu Yong,Lin Guangmin.Evolutionary Programming Made Faster[J].IEEE Transactions on Evolutionary Computation,1999,3(2):82-102.
编辑 刘 冰
A New Design Criteria of Particle Swarm Topology
MA Shenglan1,YE Dongyi2,YANG Lingling2
(1.Science and Technology Service Center,Fujian Rural Credit Union,Fuzhou 350001,China; 2.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China)
The ability of taking both the exploitation and exploration into account is a key to ensure good performance of the Particle Swarm Optimization(PSO)algorithm.This ability is to a large extent associated with the topological structures used in the algorithm.Most commonly used topologies are usually not quite favorable for assuring this ability,leading to the so-called dilemma of exploitation and exploration.This paper proposes a new design criteria for topologies by introducing such factors as low coordination number,high packing density and 3D structure.According to this rule,a new neighborhood topology for PSO is designed.The new topology,named rhombic dodecahedron,usually is used in crystallology and formed by packing spheres in hexagonal lattice and face-centered cubics,turns out to be of a 3D-close packing with the maximum space utilization with a low average coordination number.Experimental results on benchmark functions show that the proposed topology has a higher probability of finding the global optimum compared with existing topologies.
Particle Swarm Optimization(PSO)algorithm;design criteria;coordination number;rhombic dodecahedron;close packing;3D structure
1000-3428(2015)01-0200-07
A
TP18
10.3969/j.issn.1000-3428.2015.01.037
马胜蓝(1986-),男,硕士,主研方向:智能计算,数据挖掘;叶东毅,教授、博士生导师;杨玲玲,硕士。
2014-01-13
2014-03-12 E-mail:msl1121@vipqq.com
中文引用格式:马胜蓝,叶东毅,杨玲玲.一种新的粒子群拓扑设计准则[J].计算机工程,2015,41(1):200-206.
英文引用格式:Ma Shenglan,Ye Dongyi,Yang Lingling.A New Design Criteria of Particle Swarm Topology[J]. Computer Engineering,2015,41(1):200-206.
