一种混合多变量公钥签名方案
2015-06-27李晓莉乔帅庭
李晓莉,乔帅庭,刘 佳
(1.河南工业大学信息科学与工程学院,郑州450001; 2.信息工程大学数字工程与先进计算国家重点实验室,郑州450001;3.防空兵指挥学院,郑州450052)
一种混合多变量公钥签名方案
李晓莉1,乔帅庭2,刘 佳3
(1.河南工业大学信息科学与工程学院,郑州450001; 2.信息工程大学数字工程与先进计算国家重点实验室,郑州450001;3.防空兵指挥学院,郑州450052)
多变量公钥密码体制能抵抗量子计算机的攻击,是后量子时代一种安全的密码体制备选方案。考虑到Square体制可有效抵抗线性化攻击,不能抵抗差分攻击,三角型密码系统能抵抗差分攻击,但受到线性化方程攻击和最小秩攻击的情况,结合Square体制和三角型密码系统,采用新的混合签名结构框架重构中心映射,提出一种混合多变量公钥签名方案。分析结果表明,混合签名方案克服了Square体制和三角型密码系统的缺陷,能够抵抗线性攻击(包含一般线性化方程攻击和高阶线性化方程攻击)、差分攻击、最小秩攻击和代数攻击,具备较高的安全性。
多变量公钥密码;混合多变量签名方案;线性攻击;差分攻击;最小秩攻击;代数攻击
1 概述
量子计算机的快速发展对信息安全体系造成极大的影响。Shor算法的提出使得目前广泛使用的基于大数分解和离散对数的公钥签名算法受到严重威胁[1-2]。为此,具有抗量子计算性质的公钥密码受到了广泛关注[3]。多变量公钥密码体制就是在这种背景下发展而来。其安全性基于有限域上多元二次非线性方程组和多项式同构问题的难解性[4-6]。
1999年,Moh提出了TTM(Tame Transformation Method)密码系统,该密码系统的中心映射为“三角型”映射[7],具有很高的效率,但受到线性攻击和最小秩攻击[8-9]。2009年,Crystal Clough提出了一种新的高效的加密方案Square,该方案能有效地抵抗线性攻击等[10],同年,Olivier Billet等通过差分攻击手段寻找Square方案的不变子空间,从而恢复出Square方案的密钥[11]。当前的多变量公钥密码算法大部分受到不同程度的攻击,如何构造出一种安全的多变量公钥加密和签名体制是一个值得研究的热点和难点。
本文利用分支思想,在Square体制和三角型密码系统基础上,重构了中心映射,设计了混合签名方案,从线性攻击、差分攻击、最小秩攻击等对混合签名方案进行安全性分析。
2 背景知识
2.1 多变量公钥密码体制的一般结构
多变量公钥密码的陷门构造如下所示:
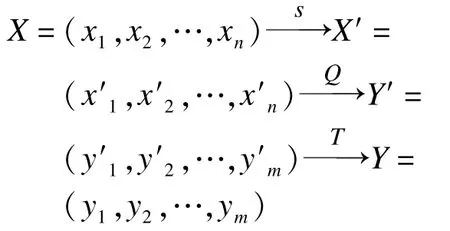
从而得到公钥:

其中,S:X➝X′=MiC+Ci和T:Y′➝Y=MTY′+CT分别为和上随机选取的可逆仿射变换,它们共同“隐藏”了中心映射Q的结构,是私钥的重要组成部分。
公钥方程组每个pk(x1,x2,…,xn)为一个关于x=(x1,x2,…,xn)的非线性二次方程:

所有的系数和变量都在域k=Fq中,q为域k的阶。
解决此类问题相当于解决了有限域上的多元二次方程组求解问题,即MQ(Multivariate Quadratic)问题[12-13]。
2.2 Square方案及其攻击
2.2.1 Square方案
2009年,Crystal Clough提出了一种新的高效的加密方案 Square,该方案能有效地抵抗线性攻击等[10]。
记k为一有限域,k=Fq,q≡3mod4。K为k的n+l次扩域,K≅k[y]/[g(y)]=Fqn+l,l满足n+l为奇数。定义k同构φ:K→kn+l,φ(a0+a1x+…+an+l-1xn+l-1)=(a0,a1,…,an+l-1),L1:kn→kn+l为一个单射仿射变换,中心映射F:K→K,F(X)=X2,L2:kn+l→kn+l为一个可逆仿射变换。Square加密体制如图1所示。

图1 Square加密体制
Square体制的公钥为:

记Square体制的密文为(c1,c2,…,cn+l)=P(m1,m2,…,mn)∈kn+l,解密如下所示:
(2)解方程X2=Y,因q=3mod4,且n+l为奇数,则|K|≡3mod4,于是可得
(3)计算(由于L1是仿射的,只有一个X是L1° φ-1的象)。
2.2.2 Square方案的攻击
2009年,文献[11]通过差分攻击手段寻找Square方案的不变子空间,从而恢复出Square方案的密钥[11]。
将Square方案的公钥分解为:

记:

DP(X,Y)=L2(2·L1(X)·L1(Y)),考虑差分DPy:X→DP(X,y)。由于L1:kn→kn+l满秩,则它的象的维数为n。任意选取线性独立的向量y1,y2,…,yn,使得DPy1,DPy2,…,DPyn能够表示{DPz}z∈E的整个空间。记Δ={P1}∪{DPyi}i=1,2,…,n,每个元素都可表示为L2°να°L1,να表示E中的元素乘以α,因而Δ={L2°νλi°L1}i=1,2,…,n,n个值λ1,λ2,…,λn未知,但线性独立。
通常的方法是找到公钥方程D1=L2°νλ1°L1∈Δ和D1=L2°νλ2°L1∈Δ之间的线性映射L,使得:


即若存在λ使得:


2.3 三角型方案及其攻击
2.3.1 三角型方案
文献[7]提出TTM(Tame Transformation Method)密码系统[7],该密码系统的中心映射为三角型映射G:

其中,gi∈Fq[x1,x2,…,xn]是任意的二次多项式。
易知G是一个一一映射,而且容易求逆:给定G(x1,x2,…,xn)=(y1′,y2′,…,yn′),可以依次求出(x1′,x2′,…,xn′):

2.3.2 对三角型方案的攻击
针对TTM三角型密码系统的攻击主要有2种:线性化方程攻击和最小秩攻击。
线性化方程攻击是指TTM密码系统存在如下的线性化方程:

其中,aij,bi,ci,d为方程式的(n+1)2个系数。
在给出O((n+1)2)个明密文对(x1,x2,…,xn,y1,y2,…,yn)时,可以求解上述方程组的系数。一旦所有的系数均被求解得到,在给定密文y=(y1,…,yn)的情况下,就可得到关于明文x=(x1,x2,…,xn)的n个线性方程组。
最小秩攻击是指把TTM密码系统的分析问题转化成求解最小秩的问题。首先把TTM系统的公钥多项式转化成二次型,然后得到该二次型下的一组n×n矩阵(M1,M2,…,Mm)。希望找到一组向量使得其中,Rank(·)表示矩阵的秩。在TTM系统中d比较小,最小秩问题在多项式时间内可以求解,也就是说最小秩攻击可以打败TTM密码系统。
3 签名方案
当前的多变量公钥密码体制中,大部分处于不同程度地攻击,构造一种安全性好的多变量公钥加密和签名方案仍是一个值得研究的开放课题。Square加密体制能够抵抗线性攻击和最小秩攻击,但是受到差分攻击的影响;三角型密码系统能够抵抗差分攻击,但不能够抵抗线性攻击和最小秩攻击。
3.1 方案描述
本文将2种方案结合起来,构造一种混合的多变量公钥签名方案。混合签名方案的结构如图2所示。

图2 混合签名方案
其中,S:和T:分别为可逆仿射变换,中心映射的构造思想类似于Square加密体制,为单射仿射变换,φ为k同构:K→km+l,φ(a0+a1x+…+,F:K→K,F(X)=X2;中心映射G:为三角型映射。

公钥包含以下内容:
(1)有限域k以及域上的加法和乘法运算;
(2)映射P=T°(+G)°S。
私钥包含以下内容:
(1)可逆仿射变换S:和
签名:设M为待签名文件,用公开的哈希函数Hash计算(x1,x2,…,x2m+l)=Hash(M)(l≪m)。签名步骤如下:
(1)计算X′=(x1′,x2′,…,x2m+l′)=S(x1,x2,…,x2m+l);
(2)选取X′=(x1′,x2′,…,x2m+l′)中的前m个分量,即(x1′,x2′,…,xm′),则其余的分量记为(xm+1′,…,x2m+l′),经过中心映射,计算Y1′=(y11′,y12′,…,y1(m+l)′)=(x1′,x2′,…,xm′)和Y2′=(y21,′y22′,…,y2(m+l)′)=G(xm+1′,…,x2m+l′),得到Y′=(y1′,y2′,…,ym+l′)=Y1′⊕Y2′=(y11′+y21′,…,y1(m+l)′+y2(m+l)′);
(3)经过仿射变换T,得到Y=(y1,y2,…,ym+l)=T(y1′,y2′,…,ym+l′)即为签名值。
验证:验证者收到消息M和签名(y1,y2,…,ym+l)后,验证如下:
(1)计算Hash(M)=(x1,x2,…,x2m+l);
(2)验证方程组P(x1,x2,…,x2m+l)=(y1,y2,…,ym+l)是否成立。若成立,则签名有效,否则,签名无效。
3.2 方案效率分析
本文方案在中心映射的设计上采用分支思想,在硬件实现上,便于进行并行化操作。不妨设消息摘要的长度为2m+l,则在一般情况下(没有采用分支时)完成签名需要在多项式时间O((2m+l)2)内完成;在本文的方案中,完成签名至多在多项式时间O(m2+(m+l)2),约为O(2m2),即签名的时间复杂度为O(2m2)。因此,方案具有很好的效率。由混合签名方案的结构可知,签名长度为(m+l)q。
4 安全性分析

目前,针对多变量数字签名方案的典型攻击方法主要有线性化方程攻击(线性攻击)、差分攻击、秩攻击、代数攻击等,当针对多变量数字签名方案的攻击算法计算复杂度均大于O(280)时,称该方案的安全强度达到O(280)。下面以选取参数q=216,m=16,l=4为例对混合签名方案进行安全分析。
4.1 线性攻击
混合签名方案的公钥P也可表示为:
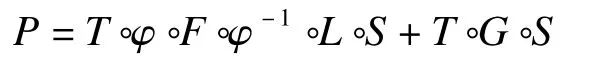
其中,T°φ°F°φ-1°L°S为Square密码体制;T°G°S为三角型密码系统。
对T°φ°F°φ-1°L°S而言,中心映射F=X2(即MI的中心映射Y=Xqθ+1中θ=0的情形)。而线性化方程攻击是利用MI类的中心映射的关系XYqθ-Xq2θY=0得到的X与Y的线性关系进行攻击的。在混合签名方案中,取θ=0,不能得到系统T°φ°F° φ-1°L°S关于X与Y的线性关系,从而得不到公钥P=T°(+G)°S中X与Y的线性关系,所以,混合签名方案可抵抗一般线性化方程攻击。
Ding等人在PKC 2007提出了针对中间域多变量公钥加密体制(MFE)的高阶线性化方程攻击[14]。考虑混合签名方案中含有三角型密码系统,需要对混合签名方案进行抗HOLE攻击分析。
由混合签名方案的公钥为:P=T°(φ°F°φ-1°L+G)°S=T°(+G)°S。在签名过程中经过变换S后,变量分为两部分(x1,′x2,′…,xm′)和(xm+1,′xm+21,′…,x2m+l′),中心映射为+G:X′→Y′,即:

类似于MFE加密方案[15],变量(xm+1′,xm+2′,…,x2m+l′)与(y21′,y22′,…,y2(m+l)′)存在高阶线性化方程,但系统加入了(y11′,y12′,…,y1(m+l)′),相当于在三角型系统中加入了外部干扰,而加入外部干扰后就打破了高阶线性化方程攻击的可能[16]。事实上,在一般情况下,在三角型系统中,中心映射的输入变量与输出变量一般不会存在特殊的关系,即不会存在高阶线性化方程关系,所以混合签名方案能抵抗高阶线性化方程攻击。
综上所述,混合签名方案可抵抗线性化攻击。
4.2 差分攻击
多变量公钥密码系统中,差分攻击主要针对中心映射形如F:X→Xql+1的体制提出[17]。
由于在系统中P1=T°φ°F°φ-1°L°S中F的特殊形式使得DP1(X,Y)=T(2·S(X)·S(Y)),从而可以寻找不变子空间来恢复密钥信息。
但混合签名方案中P=T°(+G)°S引入了中心映射G,G不是形如G:X→Xql+1的映射,整体中心映射的结构发生变化,且引入G后条件DP(X,Y)=T(2·S(X)·S(Y))也不能满足,针对Square的攻击也不适应于新的混合签名方案,所以,利用差分手段对混合签名方案进行攻击不可行。
4.3 秩攻击
考虑到针对三角型密码系统的攻击主要是最小秩攻击,这里的秩攻击特指最小秩攻击。最小秩攻击的复杂度为qtr(w2(nt/2-w/6)+wn2t)~O(qtrw3),其中,;r各方程的线性组合所能达到的最小秩;n为方程组中变量的个数;w为方程的个数[18]。由给出的参数可知,混合签名方案中q=216,m=20,n=36,从而t=1。将中心映射转为可以利用的矩阵形式,将公钥转为20个36×36的矩阵,r为公钥矩阵的一组线性组合达到的最小秩。只要保证r≥5,最小秩攻击的复杂度就大于O(280)。
在三角型密码系统中,通常r的取值很小,比如TTM体制,r=2,所以三角形系统容易受到最小秩攻击[7]。在混合签名方案中,引入了Square方案,从而使得r增大,所以20个36×36的矩阵的线性组合的秩很容易满足r≥5。
综上,在参数选取合适的情况下,混合签名方案可抵御最小秩攻击。
4.4 代数攻击
代数攻击是直接针对公钥方程组的,常用的工具包括Gröbner基攻击和XL算法[19-20]。
根据方程的个数m和变量的个数n之间的关系,代数攻击分为m=n,m>n和m<n3种情况进行。但在混合签名方案中,方程的个数为m+l,变量的个数为2m+l>m+l,所以仅就m<n的情形进行讨论。当m<n时,多元二次方程组为不定方程组[11],求解的复杂度约等于穷尽搜索的复杂度O(qm)。在本文方案中,参数q=216,m=20,复杂度为O(2320),所以,混合签名方案能够抵抗代数攻击。
5 结束语
本文结合Square体制和三角型密码系统,构造了新的中心映射,提出一种混合的多变量公钥签名方案。由安全性分析可知,该方案克服了Square体制和三角型密码系统的缺陷,能够抵抗线性攻击、差分攻击、最小秩攻击和代数攻击。本文签名方案参数的选取以及是否存在对其新的攻击是下一步要研究的问题。
[1] Shor P.Polynomial-time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer[J].Aiam Journal on Scientific Computing,1999,41(2):303-332.
[2] Fu Xingqun,Bao Wandu,Zhou Chun.Speeding up Implementation for Shor’s Factorization Quantum[J]. Chinese Science Bull,2010,(4):322-327.
[3] Bernstein D J,Buchmann J,Dahmen E.Post-quantum Cryptography[M].Berlin,Germany:Springer,2009.
[4] Ding Jintai,Yang B Y.Multivariate Public Key Cryptography[M].Berlin,Germany:Springer,2009.
[5] 孙昌毅,李益发,斯雪明.基于多变量公钥密码体制的代理重签名方案[J].计算机工程,2012,38(17): 116-118.
[6] 乔帅庭,韩文报,李益发,等.基于外部干扰的中间域公钥签名方案的优化[J].信息工程大学学报,2013, 14(2):135-140.
[7] Moh T.A Public Key System with Signature and Master Key Functions[J].Communications in Algebra,1999, 27(5):2207-2222.
[8] Goubin L,Courtois N T.Cryptanalysis of the TTM Cryptosystem[C]//Proceedings of Asiacrypt’ 00. Berlin,Germany:Springer,2000:44-57.
[9] Tsujii S,Gotaishi M,Tadaki K,et al.Proposal of a Signature Scheme Based on STS Trapdoor[EB/OL]. (2004-05-20).http://www.eprint.iacr.org/2004/366.
[10] Clough C,Baena J,Ding J T,et al.Square,A New Multivariate Encryption Scheme[C]//Proceedings of CT-RSA’09.Berlin,Germany:Springer,2009:252-264.
[11] Billet O,Macario-Rat G.Cryptanalysis of the Square Cryptosystems[C]//Proceedings of ASIACRYPT’09. Berlin,Germany:Springer,2009:451-468.
[12] 孙昌毅,李益发,张文政,等.基于多变量密码体制的新型代理签名方案[J].四川大学学报:自然科学版, 2013,49(3):565-569.
[13] 陶 羽.多变量数字签名的研究与设计[D].西安:西安电子科技大学,2012.
[14] Ding J,Hu L,Nie X,et al.High Order Linearization Equation(HOLE)Attack on Multivariate Public Key Cryptosystems[C]//Proceedings of PKC’07.Berlin, Germany:Springer,2007:233-248.
[15] Wang L C,Yang B Y,Hu Y H,et al.A“Medium-field”Multivariate Public-key Encryption Scheme[C]// Proceedings of CT-RSA’06.Berlin,Germany:Springer, 2006:132-149.
[16] Tian L,Bao W S.A Medium Field Multivariate Public key Signature Scheme with ExternalPerturbation[C]// ProceedingsofCorference on IntelligentInformation Technology and Security Informatics.[S.1.]:IEEE Perss, 2010:753-757.
[17] Fouque P A,Granboulan L,Stern J.Differential Cryptanalysis for Multivariate Schemes[C]//Proceedings of EUROCRYPT’05.Berlin,Germany:Springer,2005: 341-353.
[18] 鲁晓彬.几类多变量数字签名方案研究[D].郑州:解放军信息工程大学,2012.
[19] Albrecht M R,Cid C,Faugère J C,et al.On the Relation Between the MXL Family of Algorithms and Gr?bner Basis Algorithms[J].Journal of Symbolic Computation, 2012,47(8):926-941.
[20] Thomae E,Wolf C.Solving Underdetermined Systems of Multivariate Quadratic Equations Revisited[C]//Proceedings of PKC’12.[S.1.]:IEEE Press,2012:156-171.
编辑 索书志
A Hybrid Multivariate Public Key Signature Scheme
LI Xiaoli1,QIAO Shuaiting2,LIU Jia3
(1.College of Information Science and Engineering,Henan University of Technology,Zhengzhou 450001,China; 2.State Key Laboratory of Mathematical Engineering and Advanced Computing,Information Engineering University, Zhengzhou 450001,China;3.Air Defense Forces Command Academy,Zhengzhou 450052,China)
Multivariate public key cryptosystem mechanism can resist attacks from the quantum computer,so it is believed to be an alternative secure cryptosystem in the post-quantum age.Considering that the Square scheme can resist linearization attack,but it can not be resistant against differential attack,and tame transformation method can resist differential attack,but it cannot be resistant against linearization attack and the minrank attack,by combining the Square scheme and tame transformation method,and using a new framework,a new central mapping is redesigned,and a hybrid multivariate public key signature scheme is proposed.Analysis results show that the hybrid signature cryptosystem has good efficiency and overcomes the drawbacks of the Square scheme and tame transformation method.Meanwhile,it can also resist linearization attack(including ordinary linearization attack and High Order Linearization Equation(HOLE) Attack),differential attack,the minrank attack and algebraic attack.
multivariate public key cryptography;hybrid multivariate signature scheme;linearization attack;differential attack;minrank attack;algebraic attack
1000-3428(2015)01-0121-05
A
TP309
10.3969/j.issn.1000-3428.2015.01.022
国家自然科学基金资助项目(61300123)。
李晓莉(1976-),女,讲师、博士,主研方向:信息安全;乔帅庭,硕士研究生;刘 佳,讲师、博士。
2014-01-14
2014-03-26 E-mail:lixiaoli201311@163.com
中文引用格式:李晓莉,乔帅庭,刘 佳.一种混合多变量公钥签名方案[J].计算机工程,2015,41(1):121-125.
英文引用格式:Li Xiaoli,Qiao Shuaiting,Liu Jia.A Hybrid Multivariate Public Key Signature Scheme[J].Computer Engineering,2015,41(1):121-125.
