地震波反演成像方法与技术核心问题分析

王华忠,冯 波,王雄文,胡江涛,李 辉

(波现象与反演成像研究组WPI，同济大学海洋与地球科学学院，上海200092)

地震波反演成像方法与技术核心问题分析

王华忠,冯 波,王雄文,胡江涛,李 辉

(波现象与反演成像研究组WPI，同济大学海洋与地球科学学院，上海200092)

常规的地震反演成像分为偏移速度分析与层析成像、叠前深度偏移(角度道集产生)和AVA分析/反演3个重要环节，其中的关键技术是当前勘探地震学中的核心技术。全波形反演(FWI)是理论意义下十分完善的地震波反演成像理论框架。原则上，FWI可以把上述3项常规的反演方法技术合为一体，给出比较理想的反演成像结果。但是，由于叠前地震数据的不完备、地震波正演模拟方法不能很好地模拟实测地震波场、初始模型不够精确、地震子波的未知和空变，使得严格意义下的FWI方法尚不能很好地解决实际问题。通过叠前地震数据和地下介质模型的特征表达，提出把经典的FWI分成透射波层析成像、最小二乘叠前深度偏移成像和反射波层析成像3个线性化反演方法的串联，构成FWI反演成像的实用化流程。针对我国陆上地震数据的特点，指出做好浅层速度模型建立、背景速度模型建立、成像道集层析速度模型建立、最小二乘叠前深度偏移成像、张角及界面倾角道集的产生以及小角度成像道集波阻抗反演，是当前推进FWI反演成像方法技术应用与发展的关键所在。

反演成像理论;多级Born近似;全波形反演;逐级线性化反演;实用化地震反演成像技术路线

现代地震勘探中，岩性油气藏的精细描述主要是利用高精度采样(宽方位、宽频带和高密度采样)的高维地震数据反演估计精细的背景参数变化(主要是速度、各向异性参数和Q值)和高保真及高分辨率的高波数参数变化(主要是反射系数)，结合岩石物理知识，进行油气预测。精细背景参数变化的估计主要是利用层析成像技术;高保真及高分辨率的高波数参数变化的估计方法主要是保真叠前深度偏移或最小二乘叠前深度偏移技术。现代地震勘探的一个主要特征是整个成像处理流程逐步进入以地震波反演成像为主的阶段，其中的每一个环节基本上都可以抽象为建立正演预测模型和Bayes参数估计两个关键步骤;另一个主要特征是现代的地震反演成像技术以岩性油气藏的描述为目标。

一般意义下的地震波成像所指的就是地震波偏移成像。它是在假设偏移速度场已知的情况下，利用在该速度场中计算的波场反向外推算子，把地表记录的波场外推到绕射点上，用适当的成像条件提取成像值，目标是定量地定位反射系数出现的空间位置，并定性地保持反射系数的相对强度，尤其是角度反射系数的相对强度。

在相对保真的叠前成像道集上，进行地震子波属性的提取及基于地震子波属性的储层识别与描述;也可以进行AVA分析/反演，进而开展半定量的储层识别与描述。显然，有比较合适的叠前地震数据、正确的背景速度场和保真的角度成像道集是进行后续的储层解释的基础。

地震波偏移成像与地震波反演成像之间的区别是明显的。原则上，前者定量地估计反射点的位置，定性地估计角度反射系数的大小;后者试图定量地估计全波数带的速度场(多参数反演情况下也包括其它参数的全波数带成分的估计)。地震波反演成像的代表性技术是全波形反演(full waveform inversion，FWI)，它的目标是估计全波数带的速度场(也可以估计全波数带的其它参数场)。

地震波反演成像的基本思想是Bayes估计理论。Tarantola详细而深入地分析了地震波全波形反演的理论问题[1-2]。Bayes估计理论更是现代信号分析中的核心内容[3-4]。在整个地震数据处理与反演成像过程中，去噪、反褶积、高维数据规则化、一维波阻抗反演、AVA(叠前)弹性参数反演、最小二乘叠前偏移成像、层析成像等都是在此框架下进行的。根据Bayes估计理论，首先假设存在一个正演预测算子，它可以预测观测数据。若预测噪声为高斯白噪，此时的Bayes估计可以在最小二乘意义下实现，此为最大似然估计方法。假设已知关于模型的先验概率分布，可以建立一个联合的后验概率分布，数据误差一般用L2范数，模型约束一般用L1或Cauchy范数等;根据正算子的线性与否，选择用线性最小二乘方法或非线性最小二乘方法求解反演问题。此为经典的Bayes估计方法。

预测观测数据的正算子十分重要。褶积算子用于反褶积;一维波动方程用于预测自激自收的地震道(波阻抗反演);自回归(auto regressive,AR)模型算子常用于线性信号预测(压制噪声);旅行时计算算子用于预测实测数据中的旅行时(旅行时层析成像);Zoeppritz方程及其各种简化形式预测角度反射系数(AVA弹性参数反演);Fourier变换算子用于预测规则无假频数据的谱(高维数据规则化);动校正时距关系预测实测CMP道集中的双曲时距关系(估计均方根速度);各种形式的波动方程预测实际观测的炮记录(全波形反演)。可以看出，每一类正算子对应一类反演问题。正算子建立了要估计的参数与观测数据之间的线性或非线性关系。实际上，很多情况下正演结果并不能很好地预测实测数据，从而导致反演结果精度降低，甚至反演过程根本不收敛。

反演问题是典型的不适定问题。在地球物理反演中，解的存在性是有物理保证的，问题主要是解的不唯一性和计算过程中解的不稳定性。二者具有关联性，计算的不稳定性加剧了解的不唯一性，但最根本的还是解的不唯一性问题。反演问题解的不唯一性本质上是由数据空间向模型空间映射的非线性性引起的，甚至是由模型参数变化的复杂性和描述波场与参数场关系的正算子决定的。不唯一性只可以减弱，不可能完全消除。反演解的不唯一性和反演解的精度可以认为是一个问题的两个方面。减弱反演解的不唯一性的关键是减弱由数据空间向模型空间映射的非线性性、提高初始模型的精度、增加关于模型的先验信息，这些措施可以有效地提高反演解的精度。目前，FWI技术发展过程中提出的所有方法都是基于上述3点的。

20世纪80年代，地震波反演处于热潮期，很多学者对全波形反演理论做了十分扎实的基础研究工作[5-10]。但受当时野外地震数据观测技术和高性能计算机技术的局限，无法将提出的理论方法转为实用。此后，一维波阻抗反演、AVA叠前弹性参数反演这些计算需求小的反演方法得到了不断发展。但从理论上看，这些反演方法都不具备高维叠前反演的潜力，对于介质分布情况的假设过多。从实用性上看，它们的反演精度从来没有被认真地考究过。可以说，这些反演结果并没有对地震解释产生过实质性的贡献。

近几年，高维叠前地震数据的全波形反演理论与方法重新成为了勘探地球物理领域的核心议题，这首先得益于地震数据采集技术和大规模高性能计算机技术的进步，其次是很多研究者对地震波高维叠前反演研究的兴起做了大量的铺垫工作[11-16]。宽方位、高密度和宽频带(尤其是低频)数据的采集技术和GPU/CPU异构计算机群技术为FWI技术的可能应用奠定了很好的基础。

但是，经典FWI技术的实际应用遇到了巨大的困难，真正成功的应用实例尚不多见。主要体现在叠前数据的不完备、地震波正演模拟方法的不完善、初始模型不够精确、地震子波的未知和空变等4个方面。近几年研究者们逐步认识到经典的FWI很难得到合适的反演解，于是提出了各种各样的FWI变种方法，基本的思想是尽量克服上述4个方面因素的影响，使得反演结果更加稳定，反演过程的收敛性更强。

从理论发展的角度看，目前以地震波偏移成像为主的叠前地震数据成像处理发展到以FWI技术为代表的地震波反演成像是无法回避的。但是，FWI方法技术的实现还是要从系统的观点出发，依据实际数据情况构建出合适的技术流程，达到FWI的目的，即得到全(宽)波数带的速度估计结果(也可以包括其它参数的估计结果)。理论上讲，FWI技术的实现等于把叠前数据采集、反演成像和储层解释有机地融合在一起。

当前对FWI方法技术的定位，一般地认为它可以提供满足逆时深度偏移(RTM)成像要求的更为精细的速度场。实质上，FWI的真实目的是得到全(宽)波数带的参数估计，类似RTM的偏移成像方法是辅助FWI得到波数带更宽的参数估计结果，而不是FWI仅仅提供一个更好的偏移速度给RTM[17]。据此可以看出，FWI是期望从叠前数据中定量地估计弹性参数(甚至岩性参数和流体参数)的技术，但是能否达到这样宏大的目标，叠前数据的质量是关键因素。

因此，本文首先从叠前地震数据的抽象认识入手，提出特征波的概念以满足不同层次的FWI对数据的要求，接着提出对参数空间及地震波传播的抽象认识，建立反演参数和特征波场之间的关系，并据此尽量强化二者之间的线性关系，同时说明正问题线性化的必要性及给出比较精确的初始模型的必要性。在此基础上，给出地震波反演成像的合理的技术流程，以达到实现全(宽)波数带的参数估计的目的。

我们认为，地震波反演成像的目的是通过弹性参数的估计来刻画和描述储层。这是下一代地震成像技术的显著特征，标志着勘探地震学全面进入反演阶段。

1 油气地震勘探中的关键问题分析

油气地震勘探的终极目标是尽可能精确地描述含油气储层。宏观地讲，这是一个更大的反问题。所依据的数据包括地震数据、测井数据、地质数据(包括基本地质认识)、岩石性质数据(包括基本岩石性质测定)，反演过程归结为一个综合判断和决策过程。当前，世界上大的地球物理服务公司都试图推出这样的综合性的软件系统，可以简称为采集、处理和解释一体化系统。但这样的系统在决策阶段存在软肋，解释方面也是以构造解释为主，含油气性的判断甚至还远没有达到半定量的程度。在反演理论大框架下，向智能化的地震数据采集、处理、解释和决策一体化方向发展是没有异议的发展方向。目前存在如下一些共识：①地震数据采集向宽方位、高密度和宽频带数据采集发展;②反演成像向全(宽)波数带参数估计方向发展的趋势已十分明显;③地震地质解释的全三维化与智能化正逐步展开。这3点的目的都是指向更精确、更智能化地描述储层。

基于地震资料描述储层时，地震波场中携带的哪些信息可以对储层的存在和储层的性质有所指示，是油气地震勘探工作者必须思考和弄清楚的问题。这也是反演理论中的基本概念，即数据中一定要包含有要反演参数的变化信息，而且二者的关联性还要足够强。

目前，可以确认的是地震数据同相轴的到达时与地震波速度、各向异性参数是有密切关系的;地震波波阻抗的变化与反射地震波振幅有密切关系;吸收衰减参数(Q值)与反射地震波的振幅有明显的关系;小尺度地下介质体的散射与地震波振幅、频率和相位存在明显的关系。充分利用上述关系来解决储层的描述和刻画是问题的关键所在。目前的地震波反演成像还远没有把上述关系利用得很彻底。

叠前地震数据是波在地下介质中传播后的累积效应，因此，利用叠前地震数据反演得到的往往也是介质性质参数变化的光滑结果。对速度、各向异性参数和Q值的估计得到的都是这样的结果。从局部平面波传播的角度看，叠前地震数据与地下介质参数之间由局部平面波传播联系起来，方位张角成像道集或方位倾角成像道集是油气储层描述最核心的基础数据。可以说，它们是成像域的高维叠前数据体，直接携带了与储层及周边岩性变化有关的信息。到目前为止，在地震反演成像过程中，产生尽可能保真的方位张角成像道集或方位倾角成像道集是进一步描述裂缝储层、孔洞储层和其它类型岩性储层的基础。对波阻抗变化、裂隙方向和密度、散射体的估计都需要在这样的道集上进行，利用成像道集上的振幅变化考察的是参数的高波数变化成分。

2 叠前地震数据的抽象认识

叠前地震反演成像依赖的是单炮道集表示的地震数据，一个探区的所有单炮道集可以表示为：

(1)

式中：Xs=(xs,ys)和Xr=(xr,yr)分别代表炮点和检波点坐标;Ns代表总炮数;R2代表炮点和检波点分布区域。

期望这样的数据是宽方位、高密度和宽频带(尤其包含低频成分)的，最好是炮点与检波点采样间隔有大致相同的空间采样率。原因可以由下列定理清楚地表明。

定理[18]：常速情况下，在一阶Born近似成立的条件下，在散射体的远场范围内，散射势F(r)与它的波数谱f(s,s0)之间存在如下Fourier变换关系：

(2)

式中：K=(ω/v)·(s-s0)，s0代表入射波方向，s代表出射波方向；r代表散射体的空间分布范围。(2)式定义了散射势F(r)和散射势的谱f(s,s0)之间的Fourier变换关系。

由(2)式可见，如果得到宽波数带的散射势谱就可以通过Fourier反变换得到高分辨率的散射势的估计。散射势与速度扰动密切相关，很多文献上都有定义。散射势的波数分布范围由K=(ω/v)·(s-s0)给出。其中，矢量s-s0定义了散射(或反射)张角，观测系统决定了张角的范围，张角范围越大，波数谱越宽，对应地，要求地震数据的观测角度越大，即要有充分长的偏移距和充分宽的方位角。其中频率范围也要求足够宽，尤其是低频成分对散射势的低波数成分贡献很大。至于叠前地震数据中的高密度采样，主要是从反假频的需要而提出的，尤其是对某些特殊的低视速度噪声需要特别密的空间采样。当然，增加覆盖次数、提高信噪比也是加密采样的基本考虑。

更进一步地，从理论上来说，地震波反演成像要求叠前地震数据采集系统对地下任何一个绕射点(反射点)都有广角度的、角度间隔均匀的、不产生采样假频的照明。同时期望每个角度的数据中仅仅有高斯白噪声;还期望各角度之间的子波特征保持一致。

目前，比较流行的经典意义下的FWI反演是利用变密度声波方程，甚至常密度声波方程进行地震波正演。当然，也有用弹性波方程进行地震波正演来预测实测炮道集的。无论采用何种波动方程都不可能很精确地预测出实际数据，其中的影响因素实在太多。不能预测的部分变成数据残差，该残差不符合Gauss分布，使得问题的非线性性变强，解的非唯一性变强。

问题的解决办法是强调对数据的预处理，而不强调使用复杂的正演模拟方程。为此，我们提出了特征波的概念。所谓特征波是指单一震相的时空局部的波，可以是反射波、绕射波或透射波，也可以是某种波的波形、包络、相位、甚至是到达时。我们认为当前的反演成像还是要先针对单一震相的波现象进行。

另一方面，我们把单炮地震数据抽象地描述为：将地表(也可以是井中或海底(OBC)等处)观测到的地震数据视为以旅行时、炮/检点坐标(或中点半偏移距)为变量的函数，它的基本特征应该是由时距关系规定的、由带限反射子波表现出的同相轴加上一定的随机噪声。速度和各向异性参数场的背景部分决定同相轴出现的位置，Q值和波阻抗变化决定反射子波的相对振幅。观测数据中子波振幅的绝对值影响因素甚为复杂，海上地震勘探还比较容易分析清楚，陆上叠前地震数据中绝对振幅的具体含义及影响因素还有待深入分析。这也说明了基于波形振幅差的一类FWI反演技术难以得到合理的反演解的基本原因。所有基于振幅的反演方法都存在需要讲清楚实测数据的振幅是什么含义的问题。据此，我们更进一步地提出，首先利用同相轴的到达时信息反演背景速度、各向异性参数,也可以引入吸收衰减旅行时反演背景Q值参数。在此基础上，进行带吸收衰减的各向异性叠前深度偏移成像，产生保真的方位张角成像道集或方位倾角成像道集，再进一步描述和刻画储层。这是目前比较现实的地震波反演成像技术路线。

更进一步地，把单炮道集中的波现象分为透射波、反射波和绕射波等。当然也包括多次波和AVA现象。对应于近偏移距的折射波和直达波的这部分透射波，主要用来进行浅层近地表速度层析反演;对应于中长偏移距的来自中深层的折射波和潜波(Diving Wave)的这部分透射波，主要用来进行中深层背景速度的估计。因为透射波是不受小尺度速度异常体的影响的，利用它也只能反演大尺度的背景速度场。目前叠前偏移成像主要用的是一次反射波和/或绕射波。RTM原则上可以对多次波成像，但需要精确的、包含正确的反射界面的速度场和修正的成像条件。若能提供这样的速度场，RTM也就没有必要了！二次反射波(绕射波)目前被用来进行反射波层析反演，估计背景速度的扰动量，提供更精确的偏移速度场。但是，仅仅考虑了Fresnel带内的二次散射波。

我们认为在这3个层次上认识地震数据，可以构造出比较合适的地震波反演成像流程。事实上，构建任何地震反演成像方法都要从叠前数据中所包含的信息能否实现反演目的出发。

3 参数空间及其中地震波传播的抽象认识

地震波在实际介质中的激发、传播和接收过程是地震波偏移成像和反演成像的基础。用一个人为构建的波传播算子预测地震波传播结果是地震波偏移成像和反演成像的核心内容。地震波在实际介质中的激发过程、传播过程和波场的检测过程是异常复杂的，而人为构建的波传播算子比较简单，仅仅描述波传播过程，且只能描述复杂的物理波场的一部分，其它的波场成分要么处理掉，要么留下来增加偏移成像噪声或者增加反演成像的不唯一性。这是地震勘探中地震数据处理流程复杂的基本原因。

我们把地震勘探所面对的地下介质抽象为横向缓慢变化的广大沉积层中分布着由于火山活动、后期地质构造运动和其它地球动力运动所产生的小尺度速度异常体，譬如地震勘探中的绕射地质体。像断层、裂缝、地层尖灭、粗糙界面、孔洞等(大)小尺度的地质异常体是常见的油气运移通道和/或储集体，对它们的刻画和描述是油气勘探的重要目的。

针对这样的介质情况，我们提出如下的抽象认识：地下介质的速度场可以分为背景速度加反射界面处的速度扰动。可用如下公式表示:

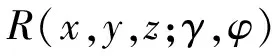
(3)

式中：v(x,y,z)是全波数带的速度场;vB(x,y,z)是其中的背景部分，δvB(x,y,z)是背景速度的扰动量;R(x,y,z;γ,φ)是方位张角反射系数。

地震数据中不同偏移距接收到的反射同相轴的到达时间取决于背景速度vB(x,y,z)或vB(x,y,z)+δvB(x,y,z);同相轴上反射波的振幅取决于反射界面处波阻抗的变化R(x,y,z;γ,φ)。不同偏移距的数据包括透射波数据(直达波和潜波)和反射波数据(一次反射波和多次反射波)。上述观察决定了地震速度反演的基本方法。

地震波在这样的介质中的传播至少可以用两种模式来描述：WRW模式和Born近似模式。WRW模式借用了Berkhout[19]常用的描述波传播的方法，它认为地下介质是光滑的背景介质加上具有一定反射系数的反射界面组成的。波在这样的介质中传播，地面观测到的数据可以由WRW模式对应的正问题来描述，即下行波场遇到反射界面反传回地表形成地面记录。原则上，这样的模式还可以描述多次波传播。Born近似模型视地下介质为背景速度加上小尺度的散射体，地表数据是所有地下散射体引起的散射波叠加形成的，可以仅仅包括一次散射，也可以同时包括多次散射。很显然，WRW模式更符合目前反射地震勘探的实际，这也是很多人把勘探地震学称为反射地震学的原因。但是，根据前面对实际地质介质的抽象，地下介质中还包括很多孤立的散射点(体)，WRW模型需要修正以便描述反射和绕射同时存在的情况下介质参数变化和对应的波场变化之间的关系。原则上，Born近似模型包含了WRW模型，但是，Born近似条件在实际应用中很难满足。本质上讲，我们还需要更好的模型来描述地下介质参数的变化和对应的波场变化之间的关系。

无论如何，当前油气地震勘探的理论主要还是建立在反射波的基础上。CMP道集处理、角度成像道集处理、AVA分析都隐含了反射波成像处理的假设，也隐含了地震波高频近似成立的假设。

基于上述参数分解方式及对应的波传播模式，可以构建出合理的地震波反演成像的实用化流程。

4 地震波反演成像的概率论观点及相应解法

综合各种文献和我们的研究经验，认为地震波反演成像技术建立在Bayes估计的理论框架上时，其理论基础最为扎实，对反演问题的认识和理解最为透彻。

首先，观测到的地震数据是随机信号，它是满足一定的概率分布的。实际上，假设地震波在实际介质中的传播的确可以由一个正问题比较精确地预测，预测结果与实测数据的残差也是随机信号。地震信号的随机性可以理解为确定性的传播波场加上不可预测的随机噪声。一般地，我们认为这部分不可预测的随机噪声满足高斯分布。因此，随机地震信号可以表示为：

(4)

式中：dobs为实测波场;F(·)为地震波正演算子;m为要反演的介质参数;η为随机噪声。(4)式是一个非线性方程组。

事实上，可以用Newton法直接解(4)式进行地震参数的反演，但是，这样做不利于认识地震参数反演问题的本质。地震波反演成像问题不是一个简单的、可以归结为非线性方程组求解的数学问题！

借助于Bayes估计的观点，对地震波反演成像的思想的理解会更为本质和深刻。Bayes估计的观点为：参数m的反演结果或估计结果应该由后验概率密度函数P(m|dobs)所定义的均值决定，即

(5)

条件概率密度P(m|dobs)可以理解为：观测数据为实测数据dobs时对应不同的参数m的概率。可见，用(5)式进行参数m的估计是非常合乎逻辑的。但是，高维参数反演情况下的后验概率密度函数P(m|dobs)几乎是无法实际计算的。

首先，利用著名的Bayes公式把后验概率密度函数P(m|dobs)的计算转化为先验概率密度函数的计算。即:

(6)

(6)式中引入了实测数据dobs对反演参数m的先验概率密度函数P(dobs|m),反演参数m本身的先验概率密度函数P(m)和实测数据dobs的先验概率密度函数P(dobs)。实测数据dobs对反演参数m的先验概率密度函数P(dobs|m)反映了用任一个反演参数m借助正演预测算子预测实测数据时预测正确的概率或预测误差满足的概率。反演参数m的先验概率密度函数P(m)的引入相当于引入了对反演参数的某种正则化约束。关于实测数据dobs的先验概率分布P(dobs)，我们一般认为是没有任何先验信息的，因此假定该先验概率分布是均匀分布，取常数值。

从统计意义上看,后验概率密度函数P(m|dobs)取最大值时对应的参数m就是所要的反演结果也是很有道理的。但是，由于(6)式中概率密度函数的形式复杂，直接对(6)式进行优化求解是非常不方便的。

因此，一般假设P(dobs|m)和P(m)这两个概率密度函数都是高斯函数，结合对P(dobs)的假设，有:

(7)

其中,C为常数,S(m)有如下的形式:

(8)

S(m)被称为代价函数。式中：CD是数据自相关矩阵;CM是模型自相关矩阵。可以明显看出,(8)式与Tikhonov正则化反演公式非常类似。说明Bayes估计理论具有更高的理论包容性，是反演理论更为完整的框架。由于指数函数的单调性质，当S(m)达到极小时，后验概率密度函数P(m|dobs)取最大值。因此，反演问题转化为求如下优化问题:

(9)

其中,H1代表参数函数取值空间,H2代表数据函数取值空间。

给出(9)式的具体求解方法之前，先分析实际地震数据反演与上述Bayes反演理论假设之间的差距。

Bayes反演理论假设实测地震波场是可以被预测的，预测结果与实测数据的残差满足高斯分布，也可以近似满足Gauss分布，即满足一类广义Gauss分布。但是，实际情况下，地震波正演模拟不可能很精确地模拟实际的地震波场。残差中既有观测随机噪声(η)，又有不能模拟的波场成分，后者有可能大于前者。这会导致残差满足或近似满足Gauss分布的假设失效，反演结果可能严重偏离实际情形。这是我们提出用特征波场或当前的地震波正演方法能较精确模拟的波场进行地震波反演的根本原因。地震子波的未知和空变也可以归结为地震波正演方法不能很好地模拟实测波场，但解决的方法是尽量不用振幅逼近，而是用波场相关或旅行时逼近来回避子波未知导致的正演波场振幅与实测波场振幅的不匹配。另一方面，实测波场的振幅影响因素非常复杂，涉及到震源与介质的耦合、实际震源的方向特征、检波器与介质的耦合、检波器本身的响应特征以及波在复杂介质中的传播过程等，并非解波动方程可以预测的。这也是理论模型数据上经典的全波形反演做得很好，而实际数据总做不好的原因。

地震波反演成像包含4个关键环节：地震波场数值模拟、模型表达(或模型参数化)、数据表达(或数据特征化)、反演方法。地震波数值模拟方法及线性化方法是反演过程中的关键问题。

(9)式描述的最优化问题的求解，从根本上讲是通过正问题的线性化把它变成一个真正的近似凸的或凸的优化问题。这应该是反问题最本质的事情[20]。一旦变成了近似凸的或凸的优化问题，其求解方法总是存在的。

将(9)式转化为近似凸的或凸的优化问题并没有现成的方法，我们认为从低尺度逐步过渡到高尺度的反演方法、利用特征波场的方法、把炮集中的波场分为透射波、反射波串联反演的方法都是化非凸优化为近似凸优化的思路和方法。

优化问题非凸，即存在多解性的根源，在于参数变化与波场变化之间的非线性性。该非线性性有两个层次，一个是实际物理层面上的，另一个是建立的数学物理模型层次上的。一般地，我们也不去区分这两个层次的差别。对非线性性的数学物理模型的线性化，就认为把一个非线性的反演问题化成了线性的，非凸优化问题就可以化为凸优化问题。实际上，我们构建的最小二乘反演问题、层析反演问题看起来都是凸优化问题，但其多解性依然很强，主要原因是数学模型层次上的线性化并不等价于实际物理层次上的线性化。

一般地，我们只解近似凸优化问题。若S(m)是凸的，最速下降方法、共轭梯度方法、Gauss-Newton方法和全Newton方法都可以较好地实现反演方法的求解。如果S(m)不是严格凸的函数，则S(m)的极小值点不再唯一，解决此类问题可以用信赖域方法、Monte Carlo方法[21]等。这些方法都可以用来求解弱非线性最优化问题，但由于Monte Carlo方法计算量大，如果没有一个比较好的策略很难实现，因此信赖域方法在这种情况下是一个比较好的选择。

对应非线性性很强的问题，难以找到一个合适的局部点(初始点)把正演问题F(m)进行线性展开得到凸性较好的S(m)。此类反演问题目前是无法求解的[22-24]。地震勘探中，小尺度异常体发育的、复杂构造探区的反演成像连构造都无法确定就是此类问题。针对此类问题，能做的工作依然是不断增加数据和参数两方面的、更丰富的信息。

对反演问题最后结果的评价原则上应该是统计决策问题，主要评价依据是反演结果的均值和方差，其中方差的意义尤其重要，它反映了反演结果的可靠程度。

事实上，Bayes参数估计是一套概念，不是一种技术。在此概念下，地震波反演成像结果的好坏由很多因素决定。对Bayes框架下地震波反演成像的本质问题的深入理解并灵活运用才是关键所在。

5 FWI反演成像实用化流程——逐级线性化反演

从前面的讨论可知，经典的FWI理论是精致而完善的，具体实现也不复杂。但是，FWI反演结果总不如理论预期。主要的问题前面已经述及，即叠前数据的不完备、地震波正演模拟方法的不完善、初始模型不够精确、地震子波的未知和空变。因此，目前关于FWI的大量研究都是试图让FWI技术能在油气勘探的实践中发挥作用。

地震波反演成像的困难从根本上讲是观测数据与反演参数之间的线性性不强，以及参数的扰动不能引起观测数据的变化(Frechet微商等于或接近于0)。前者说明反演问题解的非唯一性，后者说明地震反演成像并非对任何参数都可以进行。目前FWI技术发展侧重的几个方面是：①修改数据残差和模型差的先验概率分布，不再要求严格满足Gauss分布;②不用数据差而是用数据相关定义泛函，强化旅行时影响，弱化子波影响和振幅匹配;③不用原反射子波，改用反射子波的包络来定义逼近泛函，弱化对数据中低频的依赖性，弱化对初始模型精确性的依赖;④不用全波场逼近，分波型进行FWI反演，甚至退化为分波型的基于包络、相位、旅行时的反演。

经典的FWI反演技术退化到分波型反演时，即认为FWI反演可以按一个流程来实现。原则上，(6)式定义的经典的FWI反演是完全自动化的反演成像技术，不需要对叠前数据进行任何预处理。实际上，对于复杂的叠前数据情况和复杂的地表情况，FWI技术要应用于实际数据，必须构建合适的反演成像处理流程。

根据我国地震数据的实际情况，我们提出如下实用化的流程(称其为“FWI反演成像实用化流程”)。

1) 利用透射波(折射波和潜波)估计背景速度vB(x,y,z)。

利用中、近偏移距数据的初至波旅行时层析可以得到近地表速度，利用中、远偏移距的低频波场(早至波波场)可以估计中、深层背景速度。

2) 利用反射波和vB(x,y,z)确定反射系数R(x,y,z;γ,φ)。

利用一次(或多次)反射和散射波进行最小二乘偏移估计反射系数，其中包括积分法的最小二乘Kirchhoff叠前深度偏移、最小二乘高斯束叠前深度偏移和波动方程类的最小二乘波动方程叠前深度偏移、最小二乘逆时偏移。

3) 利用反射波和vB(x,y,z)，R(x,y,z;γ,φ)，确定δvB(x,y,z)，并更新背景速度，即vB(x,y,z)⟸vB(x,y,z)+δvB(x,y,z)。

利用背景速度和步骤2)估计的反射系数反偏移产生一次反射波。通过与实测的一次反射波逼近进行波动理论层析，也可称反射波FWI，估计背景速度的扰动δvB(x,y,z)。此时同样可以利用全波形(相位或到达时)或包络波形(包络相位)等。

其中，步骤2)和步骤3)需要迭代执行，直到方位张角成像道集整体拉平为止。在此基础上，利用小角度反射系数可以进入波阻抗(或密度)反演阶段。

上述3步流程中的核心技术都是一种线性化的反演方法，我们把这样的FWI实现方式称为逐级线性化反演或串联线性化反演。一般地，每项技术都可以进一步利用特征波的概念来实现，把复杂的波进一步分为单个震相，增加它们的实用化程度。

与上述流程相对应，还存在一个目前石油工业界正广泛使用的成像处理流程，产生保真的方位角度成像道集是其核心。该流程称为“常规叠前深度偏移成像处理流程”，可以简述如下：

2) 水平层状介质假设下动校正与速度分析技术——估计背景速度vB(x,y,z);

3) 叠前偏移剩余速度分析——估计速度扰动量δvB(x,y,z);

4) 角度成像道集层析速度反演——估计速度扰动量δvB(x,y,z);

5) 波动方程叠前深度偏移——估计方位角度反射系数R(x,y,z;γ,φ)。

值得注意的是，上述两个流程都可以包容各向异性参数、甚至Q值的估计。

对比上述两个流程：二者的目标是一致的，都是希望得到全(宽)波数带的速度成分;二者的重要差异在于对背景速度的估计上。FWI反演成像实用化流程用透射波(直达波、折射波和潜波)估计背景速度。存在低频长偏移距观测数据时，炮集中早至波成分主要是折射波和潜波，它们来自中深层。利用这些波现象进行FWI可以估计背景速度vB(x,y,z)，且所建立的背景速度的精度要高于常规叠前深度偏移成像处理流程。用低频长偏移距的透射波估计背景速度是当前FWI对实际数据处理的切实贡献。在很多海上数据的FWI处理中，都是因为背景速度精度的提高改善了成像质量(但改善并不显著)。这就容易令人产生错觉：FWI是为了提高偏移速度精度而存在的。而实质上，FWI的目标是得到全(宽)波数带的参数估计，它试图提供高精度的弹性参数估计结果，直接进入岩性储层的解释。当然，当前的常规叠前深度偏移成像处理流程本质目的也是得到全(宽)波数带的参数估计，但它往往定位在提供保真的方位角度成像道集上，基于此进入岩性储层的解释阶段。

6 陆上地震数据反演成像技术发展的关键问题

针对我国陆上地震数据的特点，推进反演成像技术发展的关键在于以下几点。

1) 减弱地表因素空变引起的子波特征空变。

陆上地表条件横向变化剧烈，导致激发接收因素空间变化，反映到每一个地震道上，接收到的反射子波受炮检点地表因素的影响。

减弱空变子波特征的影响首先是在估计背景速度的变化时充分利用到达时信息和相位信息，少用或不用振幅信息。其次是做好子波空变特征的一致性处理。

2) 充分利用初至波和早至波信息。

陆上数据的反射波和绕射波信噪比低，初至波和早至波一般而言具有更高的信噪比。但是，目前往往仅仅有中、小偏移距的初至波到达时被用来进行近地表速度层析，而具有较高信噪比的初至波和早至波数据没有得到充分的研究和利用。

3) 背景速度估计与建模。

陆上数据一般缺乏低频长偏移距数据，很难期望用透射波FWI估计背景速度vB(x,y,z)。仅仅靠动校正和均方根速度估计在信噪比低和横向速度变化大的情况下估计背景速度，其精度是远远不够的，这会导致后续的背景速度扰动δvB(x,y,z)估计不收敛，无法提高成像质量。

背景速度vB(x,y,z)的估计是一个非线性反演过程。我们提出用基于Kirchhoff PSDM和成像道集拉平的Monte Carlo反演方法估计横向变速情况下的背景速度。在2014年SEG年会中，Sajeva等用Monte Carlo方法反演背景速度为后续的FWI提供初始速度模型[25]。

4) 做好角度成像道集的层析速度反演和建模。

角度成像道集中射线层析与建模是当前深度速度建模的主力工具。但是，它的估计精度与正则化思想与方法是密切相关的。最近几年因为现代图像处理技术的引入，反射界面有机地融入反演速度场中，极大地提高了估计精度。

对于陆上地震数据的角度成像道集的层析速度反演，在提高角度道集质量、自动拾取剩余时差、自动反射界面解释及估计倾角、Beam层析、正则化和预条件等方面的改进会显著提高估计精度。另外，角度成像道集的层析速度反演与各向异性参数和Q值反演可以方便地融为一体，实现多参数联合建模。

5) 做好最小二乘反演成像。

在上述几步工作的基础上，叠前深度偏移成像的目标就是至少做到生成保真的方位角度反射系数道集。我们认为，从实用的角度看，Kirchhoff积分角度域最小二乘偏移成像和单向波最小二乘偏移成像是比较具有广泛实用意义的。最小二乘RTM的计算量太大，难以大规模地应用于实际数据的成像处理中。

6) 做好波阻抗反演工作。

波阻抗是与岩性变化关系更密切的参数。地震波反演成像的目标至少应提高到对波阻抗的反演成像上。简单地看，波阻抗与反射系数是积分和微分的关系。后者是前者的微分，反之，前者是后者的积分。从FWI反演成像角度看，小角度的反射系数与波阻抗的关系更为密切。Zhang等[26]和Duan等[27]在SEG论文中提及用小角度反射系数估计波阻抗的方法。

上述6个关键点是针对陆上地震数据进行反演成像提出的，也可以把它们组成一个流程。与FWI反演成像实用化流程相比，它更有可能促进反演成像方法技术的普及应用。

另外，特别值得关注的是，陆上地震数据噪声远大于海上地震数据，波场特征分解的思想更应体现在陆上地震数据的FWI反演成像过程中，一是提高信噪比，二是降低正演模拟复杂波场的难度(特征波场正演模拟比全波场模拟简单)。另一方面，背景部分的速度估计并不需要像叠前深度偏移那样要求数据很规则，利用波场的特征波分解可以把高信噪比的部分数据分出来，仅仅用这部分数据更新背景速度的扰动。

信号的特征提取对整个信号处理的诸多方面(譬如数据规则化、数据压缩、数据采样、去噪等)都有重大影响，波场的特征分解在反演成像中同样会非常重要。2014年SEG年会中已有作者关注波场特征分解与FWI反演数据预处理的关系[28]。

陆上地震数据的FWI反演成像需要构建更现实的技术流程。若上述6个问题解决得比较好，而且每个阶段的反演方法中正则化思想运用得当，陆上地震数据的FWI反演成像会逐步向前推进。

7 地震波反演成像中的正则化与预条件

地震波反演成像的不唯一性和不稳定性是其典型的特征，得到稳定解的基本方法是正则化。正则化是地震波反演成像实用化过程中必须考虑的问题。

理论上，地震波反演成像只能进行线性反演或弱非线性反演(可以线性化的反演)。不失一般性，可以对非线性的波场和参数之间的关系进行如下线性化处理:

(10)

(10)式可以简写为矩阵方程：

Ax=b

(11)

(11)式用来估计在m0点附近的δm。其中，x=δm，b=F(m)-F(m0)是数据残差。

由于数据和稀疏矩阵中都存在误差，(11)式本身具有欠定或超定性质，矩阵A不满秩,一般地，我们把对(11)式的求解化为二次型泛函的求解问题：

(12)

其中，R是正则化算子。从前面反演问题的概率论认识中可以看出，对于(8)式右端项中的数据误差项和模型误差项，都希望是满足高斯分布的。我们知道，当正演算子能模拟实测信号时，数据项是比较符合高斯分布的，但模型项不容易符合高斯分布。为此，我们需要对模型进行预处理，基本的思想是对它施加粗化算子，使它接近符合高斯分布，Laplace算子就是其中一种选择。

从另一个角度看，反问题求解时，参数的光滑部分(低波数部分)是容易首先求解的。那么我们可以引入一个光滑算子S，作用于原参数上，即：

y=Sx

(13)

y是参数的光滑部分。把(13)式代入(11)式得到:

AS-1y≈b

(14)

可以看出估计y要容易得多，非唯一性也降低了很多。

另一方面，不同数据分量的可靠性不同，需要引入加权系数。假设加权矩阵算子为L，代入(14)式得到：

LAS-1y≈Lb

(15)

(15)式实质上是引入了对于数据的正则化处理。

对比(8)式可以看出，关于模型的正则化和数据的正则化，实质上是试图弥补(12)式中丢弃了模型协方差阵和数据协方差阵的影响。对协方差阵的地球物理意义的理解可以帮助更好地选择(13)式和(15)式中的正则化算子。

假如对矩阵A进行SVD分解(A=U∑VT)，并代入(15)式，可以得到：

LU∑VTS-1y=Lb

(16)

其中，U为左奇异矩阵，V为右奇异矩阵。

为了对比，(11)式引入奇异值分解结果：

U∑VTx=b

∑VTx=UTb

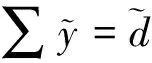
(17)

对比(16)式和(17)式，可知正则化算子L和S-1的选择更基本的含义是对数据和参数引入不同的变换矩阵，使得数据中的特征成分和参数中的特征成分建立起一对一的、线性的关系。

这是最彻底的数据特征化表示和模型特征化表示。尽管上述思想不能用在大规模地震反演成像中，但它的启发意义是深远的。对数据、对参数进行多尺度特征分解，在此基础上进行反演是提高反演过程稳定性的重要思想和手段。

针对(12)式，梯度导引类的迭代反演方法的预条件主要是对梯度场进行的，其中包括施加(近似)Hessian矩阵逆的方法，也有直接对梯度进行各种预处理的方法，这里不再赘述。TV正则化方法是十分值得关注的，很多文献上有具体的讨论，此处也不再赘述[23]。

8 结束语

地震波反演成像的基础是多次覆盖的数据体。目前叠前数据采集的最高技术是同时源激发进行宽频带、宽方位和高密度的叠前数据采集。利用这样的数据体对不特别复杂的地质构造进行偏移成像可以给出高精度的偏移成像结果;但是若地质情况特别复杂，即使较为可靠的偏移成像结果也难以得到。这主要不是偏移成像技术存在问题，而是估计精细偏移速度的反演成像技术存在问题。

数据体包含的基本信息是时距关系决定的波前面的到达时和波阻抗变化引起的波前面上的子波振幅变化。到达时信息是波传播的累积效应。波前面上的子波振幅变化是承载在到达时上的速度突变的反映。到达时对应速度场的背景变化，子波振幅变化对应速度场的跃变。据此，要反演的参数场一般可以表达为背景部分和跃变部分。对应地，可以抽象出反射波在这样的参数场中的传播模式。

在数据表达模式、参数表达模式和波传播模式的基础上，可以很自信地构建出适合不同数据情况的反演成像处理流程。旅行时与背景速度和背景各向异性参数之间的关系是近似线性的，可以构建出有效的反演方法技术，一般可以满足偏移成像方法技术的需要，给出较为精确的成像效果;地震波振幅与速度(波阻抗)扰动之间的关系十分复杂，目前基于地震波振幅的反演结果的精度还不能满足储层描述的需要。

反演成像的目标是得到全(宽)波数带的参数估计结果。以逆时偏移成像(RTM)技术为标志的、目的主要是刻画复杂构造界面形状的偏移成像技术已经发展到了接近成熟的阶段。地震成像技术的发展很快会转到以估计地下介质弹性参数为目标的反演成像技术上来。其中，各种层析成像技术(估计参数的背景变化)和最小二乘偏移成像技术(估计波阻抗的扰动)会成为两项核心技术。

另外，把要反演的参数场视为一个图像，它由纹理(高波数部分)和背景(低波数部分)组成，在反演过程中同时演化纹理的几何和背景的大小并达到收敛，是地震速度(也包括其它参数)反演的合理思想。现代图像处理中的模式提取、模式识别和模式演化会对地震波反演成像产生很强的借鉴意义和促进作用。

[1] Tarantola A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984，49(8)：1259-1266

[2] Tarantola A.Inverse problem theory and methods for model parameter estimation[M].Philadelphia,USA:SIAM,2005:1-352

[3] Kay S M.Fundamentals of statistical signal processing,volume Ⅰ:estimation theory[M].USA:Pearson Education,Inc,1993:1-625

[4] Kay S M.Fundamentals of statistical signal processing,volume Ⅱ:estimation theory[M].USA:Pearson Education,Inc,1998:1-672

[5] Beylkin G.Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform[J].Journal of Mathematical Physics,1985,26(1)：99-108

[6] Bunks C,Salek F M,Zaleski S,et al.Multiscale seismic waveform inversion[J].Geophysics,1995,60(5)：1457-1473

[7] Lailly P.The seismic inverse problem as a sequence of before stack migrations:conference on inverse scattering[J].Expanded Abstracts of Theory and Application,Society for Industrial and Applied Mathematics,1983,206-220

[8] Mora P R.Nonlinear two-dimensional elastic inversion of multi-offset seismic data[J].Geophysics,1987,52(9)：1211-1228

[9] Mora P R.Elastic wavefield inversion of reflection and transmission data[J].Geophysics,1988，53(6)：750-759

[10] Nolet G.Seismic tomography with applications in global seismology and exploration geophysics[M].Holland:D.Reidel Publishing Company,1987:1-386

[11] Pratt R G,Worthington M H.Inverse theory applied to multisource cross-hole tomography,part I:acoustic wave-equation method[J].Geophysical Prospecting,1990,38(3):287-310

[12] Pratt R G.Inverse theory applied to multi-source cross-hole tomography,part II:elastic wave-equation method[J].Geophysical Prospecting,1990,38(3):311-330

[13] Pratt R G.Seismic waveform inversion in the frequency domain,part I:theory and verification in a physical scale model[J].Geophysics,1999,64(3):888-901

[14] Biondi B,Symes W.Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging[J].Geophysics,2004,69(5)：1283-1298

[15] Lambaré G,Virieux J,Madariaga R,et al.Iterative asymptotic inversion in the acoustic approximation[J].Geophysics,1992,57(9):1138-1154

[16] Shin C,Cha Y H.Waveform inversion in the Laplace-Fourier domain[J].Geophysical Journal International,2009,177(3)：1067-1079

[17] Gray S H.Seismic imaging and inversion:what are we doing,how are we doing,and where are we going?[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014,4416-4420

[18] Born M,Wolf E.Principles of Optics[M].7thedition.United Kingdom:Cambridge University Press,1999:1-985

[19] Berkhout A J.Combining full wavefield migration and full waveform inversion,a glance into the future of seismic imaging[J].Geophysics,2012,77(2):S43-S50

[20] Boyd S,Vandenberghe L.Convex optimization[M].United Kingdom:Cambridge University Press,2004:1-727

[21] Mosegaard K,Tarantola A.Monte Carlo sampling of solutions to inverse problems[J].Journal of Geophysical Research,1995,100(B7)：12431-12447

[22] Menke W.Geophysical data analysis:discrete inverse theory[M].USA:Academic Press,Inc,1984:1-289

[23] Vogel C R.Computational methods for inverse problems[M].Philadelphia,USA:SIAM,2002:1-183

[24] Aster R C,Borchers B,Thurber C H.Parameter estimation and inverse problems[M].USA:Elsevier Academic Press，2005:1-360

[25] Sajeva A,Bienati N,Aleardi M,et al.Estimation of velocity macro-models using stochastic full-waveform inversion[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014,1227-1231

[26] Zhang Y,Ratcliffe A,Duan L,et al.Velocity and impedance inversion based on true amplitude reversetime migration[J].Expanded Abstracts of 83rdAnnual Internat SEG Mtg,2013,949-953

[27] Duan L,Zhang Y,Peng L Z.Band-limited impedance perturbation inversion using cross-correlative least-squares RTM[J].Expanded Abstracts of 84thAnnu-al Internat SEG Mtg,2014,3720-3725

[28] Bi H B,Lin T.Impact of adaptive data selection on full waveform inversion[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014,1094-1098

(编辑：陈 杰)

Analysis of seismic inversion imaging and its technical core issues

Wang Huazhong,Feng Bo,Wang Xiongwen,Hu Jiangtao,Li Hui

(WavePhenomenaandInversionImagingResearchGroup(WPI),SchoolofOceanandEarthScience,TongjiUniversity,Shanghai200092,China)

The conventional seismic inversion imaging is divided into migration velocity analysis (MVA) and tomography,prestack migration imaging and AVA analysis/inversion.The key techniques in the three inversion imaging methods are the core technologies of modern exploration seismology.Full waveform inversion (FWI) is a complete theoretical framework of seismic inversion imaging,and which can roll up the three conventional inversion imaging methods into one and give a desired imaging result in principle.However,due to the incompleteness of pre-stack seismic data,imperfectness of forward model,inaccuracy of initial model,unknown and spatial variation of seismic wavelet,the practical problems have not yet been solved with FWI method in the strict sense.In this paper we analyze the existing problems of classical FWI method and propose a practical seismic inversion imaging workflow,that is to divide classic FWI into transmissive wave tomography,LS-PSDM imaging and reflections tomography.Aimed at the features of land seismic data,we point out that the establishment of shallow velocity model,background velocity model,velocity model for CIG tomography,LS-PSDM imaging,generation of the incident angle gather and dip angel gather,impedance inversion by small angel CIG gathers are crucial for the promotion of the application and self-development of FWI technique.

the inversion imaging theory,multistage Born approximation,full waveform inversion (FWI),stepwise linearization inversion,practical seismic inversion imaging route

2015-01-03;改回日期：2015-01-27。

王华忠(1964—)，男，教授，主要从事地震波传播、地震数据分析和地震波反演成像方面的研究工作。

国家重点基础研究发展计划(973计划)(2011CB201002)、国家自然科学基金(41374117)和国家科技重大专项(2011ZX05005-005-008HZ，2011ZX05006-002，2011ZX05023)共同资助。

P631

A

1000-1441(2015)02-0115-11

10.3969/j.issn.1000-1441.2015.02.001