具有增益调度切换增益的永磁同步电机滑模控制

金宁治，张忠民，刘端增

（1.哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨150080；2.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

1 引言

永磁同步电机（PMSM）是一个多变量、非线性、强耦合的系统，对系统内部参数摄动及外部干扰极为敏感，因此传统的线性控制方法无法准确描述系统的稳态、动态过程，也无法适应系统参数的变化，从而难以保证电机在全局转速、转矩范围内的运行品质。滑模控制（SMC）是一种特殊的非线性控制，它具有响应快速、鲁棒性好、工程实用性强等优点［1-3］。然而，滑模控制不可避免带来系统抖振，因而如何消除抖振成为将滑模控制理论应用于实际电机驱动系统的关键问题［4-9］。

许多实际系统模型的结构及参数常常会随着外部环境、运行条件的变化而变化，这就要求其控制器的结构及参数能够同样随之作出实时调整，以使系统在运行范围内具有满意、一致的控制性能。增益调度控制是一种解决非线性系统控制问题的有效方法。该方法采用将一个非线性设计任务分解成一簇线性子任务的设计思想，并通过调度变量建立各个局部线性子任务之间的联系，从而构造出一种能够满足全局性能要求的非线性控制器。这一设计思想首先得到了飞行控制系统设计师们的认可，并大量应用于导弹、飞机等飞行器控制系统及机炉、风力发电等工业控制系统中［10-12］。

本文借鉴文献［13-15］的设计思想，提出了一种增益调度和自适应相结合的滑模控制器切换增益的整定方法。该方法首先根据电机实际转速—转矩运行条件，采用自适应方法实时调整切换增益的边界范围，以保证滑模控制系统的鲁棒性；同时在允许边界范围内对切换增益系数进行增益调度，以使系统获得最优控制性能。

2 滑模控制器的设计

2.1 状态空间方程

永磁同步电机在d-q同步旋转坐标系中的定子电压方程为

式中：ud，uq分别为d，q轴定子电压；id，iq分别为d，q轴定子电流；Ld，Lq分别为d，q轴定子电感；Rs为定子相电阻；Ψf为转子磁链；ωe为转子电角速度。

对于电流环控制系统，将d，q 轴定子电流误差ed，eq定义为状态变量，将d，q轴定子电压ud，uq定义为控制输入，则由式（1）可得d-q轴电流控制系统的状态空间方程为

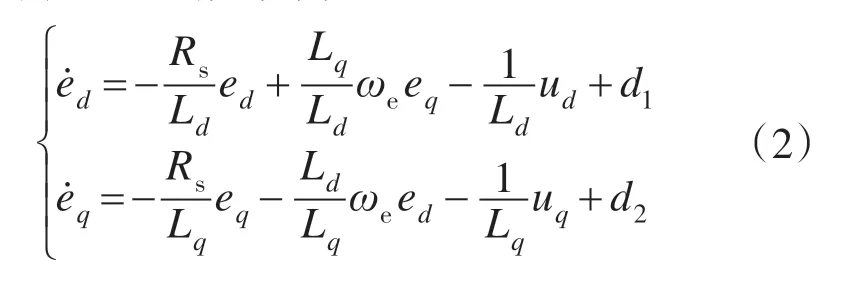
其中ed=idr-ideq=iqr-iq

式中：idr，iqr分别为d，q轴电流给定。

2.2 滑模面设计

当遭遇随机的外部扰动时，采用普通滑模面设计可能带来稳态误差，以至于达不到要求的性能指标；而采用积分滑模面设计能够消除系统稳态误差，提高控制精确度。

对于d-q 轴电流控制系统，积分滑模面表示为

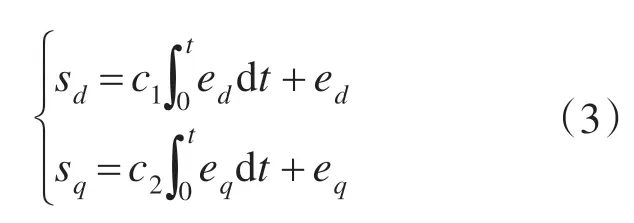
式中：c1，c2分别为d，q轴滑模面的积分系数。

2.3 趋近律设计

指数趋近律能够在获得快速趋近的同时削弱抖振。然而，它的滑模运动区为带状，即系统状态最后不是趋近于原点，而是趋近于原点附近的一个抖振。这可能激发系统建模中未考虑的高频成分，增加控制器的负担。

对于d-q 轴电流控制系统，指数趋近律表示为

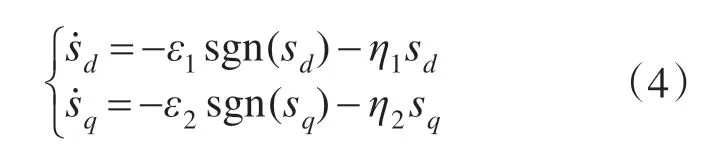
式中：ε1，ε2分别为d，q轴趋近律的切换增益系数；η1，η2分别为d，q轴的趋近律指数系数。

为了削弱滑模运动引起的高频抖振，将趋近律中的符号函数代替为如下的连续的平滑函数：

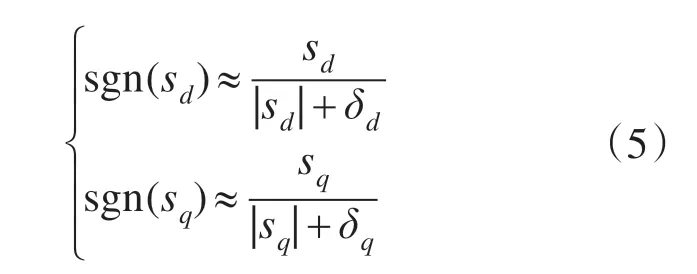
式中：δd，δq分别为d，q轴平滑函数的平滑系数。

综上所述，由式（2）、式（3）和式（4），将d1，d2视作干扰项，求得d-q 轴电流滑模控制器的控制律为

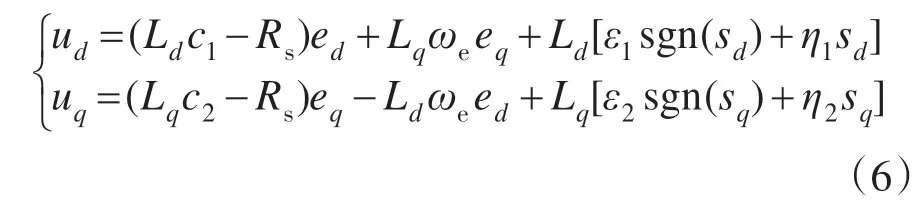
2.4 鲁棒性分析

根据Lyapunov稳定性理论，滑动模态的存在性和可达性条件表示为

对于d-q 轴电流滑模控制系统，s=[sdsq]T，则可将上式改写为

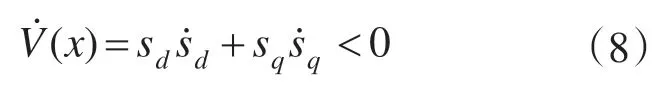
将式（2）、式（3）和式（6）代入上式，可得电流滑模控制系统的鲁棒性条件为

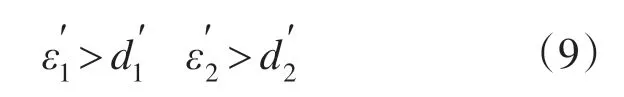
其中

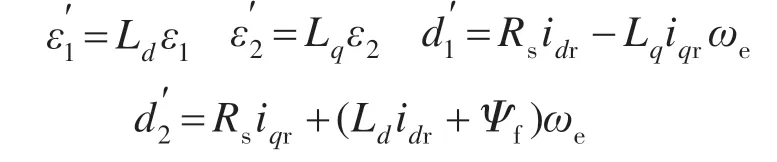
由此可以看出，在控制律式（8）中，切换增益系数ε1，ε2需要随着参数摄动和外部扰动变化，才能满足系统鲁棒性条件。然而，增大切换增益会加剧系统抖振，而减小切换增益会延缓系统动态响应。因此，需要权衡以上两种情况选择合适的切换增益系数。

所设计电流滑模控制器结构图见图1。

图1 电流滑模控制器结构框图Fig.1 Structure diagram of current sliding mode controller

3 滑模控制参数的增益调度

3.1 增益调度规则

如果切换增益系数εi(i=1,2)较小，则运动点趋近滑模面的速度较小，引起的系统抖振较小；而如果εi较大，则运动点到达滑模面时的速度较大，引起的系统抖振也较大。因此，切换增益系数εi的增益调度规则为：在距离滑模面较远处选取较大的εi，以保证快速趋近；而在距离滑模面较近处选取较小的εi，以减小系统抖振。

3.2 切换增益边界的自适应整定

如果考虑电机处于电动运行模式，d 轴电流给定idr＜0，q轴电流给定iqr＞0；一般情况下，电机电磁参数满足Ldidr+Ψf＞0；忽略干扰项中相对较小项Rsidr，Rsiqr。那么，。因此，根据式（9）可知，d轴切换增益系数ε′1的边界范围与无关；而q轴切换增益系数的边界范围要考虑的限制，即如果取值过小，则无法保证滑模控制系统的鲁棒性；如果取值过大，则不利于减小系统抖振。

鉴于以上因素，本文提出根据交轴电流给定idr和电角速度ωe对切换增益的边界范围进行自适应整定的方法。将关于切换增益的边界的自适应调整律设计为

式中：ks为切换增益边界的调整系数，ks为大于1 的常数。

在满足式（9）的前提下，考虑一定程度的参数摄动、外部干扰和转速测量误差等，综合衡量系统抖振与超调量、调节时间等动态指标，调整系数ks一般取1.3～2.2。因此，q轴切换增益系数的边界范围可表示为

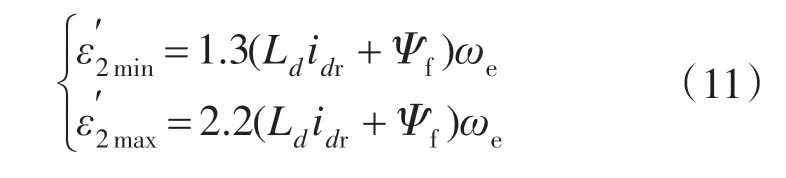
3.3 切换增益的增益调度

增益调度方法在滑模控制中的应用主要有两种形式：1）采用增益调度方法对滑模控制器网络进行调度；2）将增益调度思想应用于滑模控制器控制参数的整定。本文着重研究对滑模控制参数——切换增益的增益调度方法。这种方法不必确定典型工作点，更不必在每个典型工作点上通过仿真或实验研究一一寻找最优参数，而只需要采用合适的设计方法确定控制参数的边界范围，并采用合适的插值方法在允许边界范围内对控制参数进行增益调度。

综上所述，以q 轴滑模面函数的绝对值|sq|作为调度变量，考虑切换增益ε′2应位于允许边界范围内，则关于q 轴切换增益的增益调度规则设计为

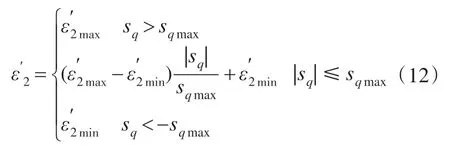
式中：sqmax为q 轴调度变量|sq|的最大值，满足-sqmax≤sq≤sqmax。

同理，关于d轴切换增益系数ε′1的增益调度规则设计为

式中：sdmax为调度变量|sd|的最大值，满足-sdmax≤分别为d轴切换增益系数的上、下边界。

4 仿真结果及分析

本文在Matlab/Simulink 环境下建立了永磁同步电机驱动控制系统的仿真模型，如图2 所示，并进行了相关的仿真研究。图2 中，外环速度控制器采用PI 控制策略；速度控制器提供定子电流幅值给定isr，根据最大转矩电流比（MTPA）矢量控制原则，isr被分配为d，q 轴电流给定idr，iqr；内环d-q 轴电流控制器采用滑模控制策略，并采用增益调度方法对切换增益进行在线整定。

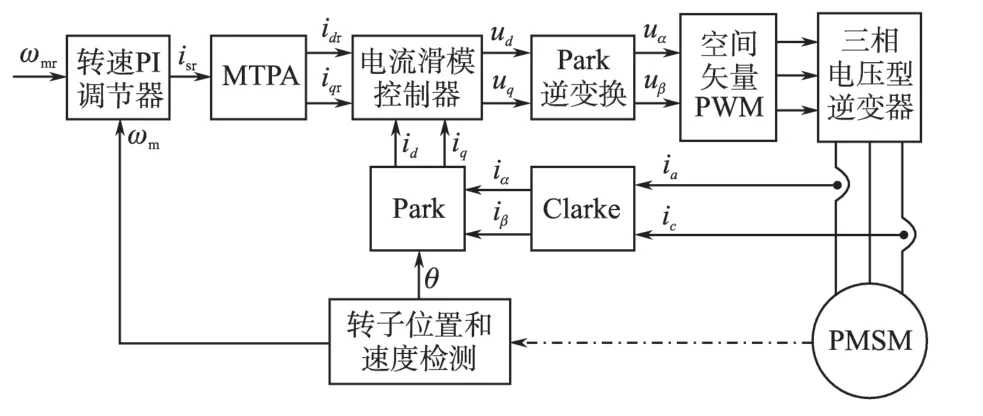
图2 永磁同步电机矢量控制系统的仿真模型Fig.2 Simulation model of PMSM vector control system

永磁同步电机样机的主要参数为：额定功率30 kW，额定转矩72 N·m，额定转速4 500 r/min，d，q轴电感分别0.13 mH，0.33 mH，永磁体磁链0.062 Wb，极对数4。

所设计滑模控制器的关键控制参数如下：d轴切换增益的边界范围为[0，185.0]；q 轴切换增益边界的调整系数ks为[1.3，2.2]；d，q轴滑模面的积分系数Ldc1，Lqc2分别为0.03，0.05。

图3 是加载动态响应曲线，其中给定转速指令始终保持为4 500 r/min，在t=2 s时刻负载转矩由36 N·m 突加至72 N·m。从图3 中可以看出，在负载突增瞬间，电流控制误差及调度变量|sq|瞬间变大，切换增益系数瞬间变小；随后电流控制误差及调度变量|sq|迅速衰减至零，切换增益的自适应边界范围，由于d轴电流给定值idr的负增长而降低。因此，在电流跟踪动态过程中，切换增益系数的变化规律符合前面所述的增益调度规则，系统电流、速度响应迅速，几乎无超调，因此所设计的电流滑模控制系统具有良好的电流跟踪特性。

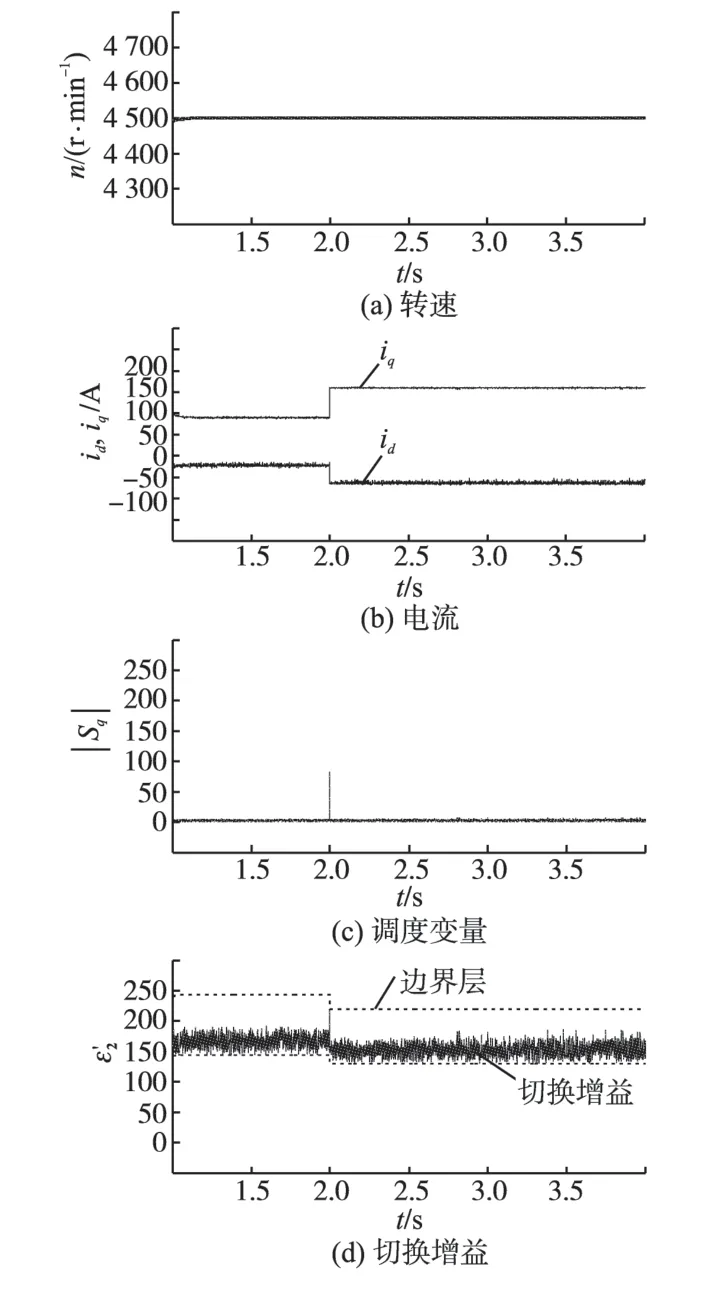
图3 加载动态响应曲线Fig.3 Responses of loading

图4 是升速动态响应曲线，其中负载转矩始终保持为72 N·m，在t=1.5 s 时给定转速指令由1 500 r/min突加至4 500 r/min。从图4中可以看出，在转速指令突增瞬间，转速控制误差较大，使得转速调节器输出较大的电流给定幅值|idr|，iqr，因而电流控制误差及调度变量|sq|瞬间变大，切换增益系数ε′2瞬间变小；由于电流环响应速度要远远高于速度环响应速度，电流控制误差及调度变量|sq|随即迅速衰减至零；在随后加速过程中，切换增益的自适应边界范围随转速逐渐升高，直至转速升高至给定转速为止。因此，在速度跟踪动态过程中，切换增益系数的变化规律符合前面所述的增益调度规则，系统速度、电流响应迅速，几乎无超调，因此所设计的电流滑模控制系统具有良好的速度跟踪特性。

图4 升速动态响应曲线Fig.4 Responses of accelerating

5 结论

本文提出了一种具有增益调度切换增益的永磁同步电机电流滑模控制方法。该方法具有以下基本特征：

1）采用自适应方法在线调整切换增益系数的边界范围，克服了常规增益调度方法需要确定典型工作点及通过大量仿真研究工作对控制参数寻优的缺点；

2）以滑模面函数为调度变量，按照增益调度规则对切换增益系数进行实时整定，使得系统在全局运行范围内具有良好的控制特性。

［1］Utkin V I.Sliding Modes in Control and Optimization Utkin［M］.Berlin：Springer，1992.

［2］高为炳.变结构控制的理论及设计方法［M］.北京：科学出版社，1996.

［3］刘金琨.滑模变结构控制MATLAB 仿真［M］.北京：清华大学出版社，2005.

［4］茅靖峰，吴爱华，吴国庆，等.永磁同步电机幂次变速趋近律积分滑模控制［J］.电气传动，2014，44（6）：50-53，62.

［5］汪海波，周波，方斯琛.永磁同步电机调速系统的滑模控制［J］.电工技术学报，2009，24（9）：71-77.

［6］Seshagiri S，Khalil H K.Robust Output Feedback Regulation of Minimum-phase Nonlinear Systems Using Conditional Integrators［J］.Automatica，2005，41（1）：43-54.

［7］林立.内置式永磁电机状态反馈线性化解耦滑模控制［J］.电气传动，2013，43（7）：49-52，62.

［8］张晓光，孙力，赵克.基于负载转矩滑模观测的永磁同步电机滑模控制［J］.中国电机工程学报，2012，32（3）：111-116.

［9］Foo G，Rahman M F.Sensorless Sliding-mode MTPA Control of an IPM Synchronous Motor Drive Using a Sliding-mode Observer and HF Signal Injection［J］.IEEE Transactions on Industrial Electronics，2010，57（4）：1270-1278.

［10］Huang Z Y，Li D H，Jiang X Z，et al.Gain Scheduled Servo System for Boiler-turbine Unit［J］.Proceedings of the CSEE，2003，23（10）：191-198.

［11］张铁军，吕剑虹，华志刚.机炉协调系统的模糊增益调度预测控制［J］.中国电机工程学报，2005，25（4）：158-165.

［12］范晓旭，白焰，吕跃刚，等.大型风力发电机组线性二次型高斯最优控制策略［J］.中国电机工程学报，2010，30（20）：100-105.

［13］胡剑波，辛海良.新型增益调度变结构控制器的性能比较研究［J］.控制与决策，2009，24（5）：769-772.

［14］申宇，仇原鹰，马伯渊.增益调度积分型切换项滑模控制器设计［J］.系统工程与电子技术，2011，33（9）：2079-2084.

［15］辛海良，胡剑波.一种新型滑模变结构增益调度控制器设计方法［J］.控制与决策，2011，26（12）：1824-1828，1834.