考虑侧风配平的工程模拟器重定位技术研究
2015-06-24吴胜亮

摘要:分析了工程模拟器重定位功能需求过程,研究了侧风配平实现过程,采用基于改进的最速下降法对侧风配平问题进行了优化计算,并在某民用飞机工程模拟器上进行了仿真验证。仿真结果表明,采用改进的最速下降法较为简单、计算量少、收敛速度快、稳定性好、易于工程实现,可以实现全飞行包线内的配平;侧风配平实现过程具备较强的可操作性,具有重要的工程应用价值,可为其它模拟器重定位技术提供重要参考。
关键词:工程模拟器;重定位技术;侧风配平;最速下降法
DOIDOI:10.11907/rjdk.151239
中图分类号:TP302
文献标识码:A 文章编号:16727800(2015)006000104
作者简介作者简介:吴胜亮(1987-),男,安徽六安人,硕士,上海飞机设计研究院助理工程师,研究方向为工程模拟器研制与试验、飞行力学、控制与仿真。
0 引言
飞机平衡状态常用于计算飞机的飞行性能,以及计算进行稳定性、操纵性分析的平衡面和分支面[2]。为确定飞行数值仿真中定常飞行的初始状态参数值,需要应用平衡状态配平算法进行配平计算。鲁可等[1]设计了基于最速下降法的配平方法,并对定常直线飞行配平进行了仿真;沈宏良等[2]设计了基于变尺度DFP算法的平衡状态和平衡面配平方法,并对定常直线爬升、正常盘旋和定直平飞平衡面进行了仿真;刘艳等[3]从飞行性能最优角度出发,充分考虑飞机本体特性及各操纵面的特性来研究多操纵面飞机的配平原则,采用数学规划法中的线性规划对配平操纵面进行分配;李洪冬等[4]利用粒子群优化算法求解飞机多种平衡状态,对飞机的稳态平飞、爬升、下降和转弯等平衡状态进行了仿真;李超等[5]设计了基于遗传算法的配平方法,并对定常直线飞行配平和水平盘旋飞行配平进行了仿真;王海涛等[6]提出只利用飞机模型的输入输出信息和配平约束条件求解配平状态的方法,采用混合遗传算法计算最优值,并对定直平飞和协调转弯进行了仿真;张剑[7]设计了一套民用喷气飞机配平计算软件,该软件可以对民用飞机的失速速度、平飞需用推力、升降舵效率、平尾效率、方向舵效率以及单发横航向稳定性等进行快速计算;徐南波[8]介绍了民用飞机单发失效时,方向舵偏度和侧滑角随着飞机配平方式变化的规律。以上学者只针对飞机定常飞行的配平进行了研究,应用不同的优化算法求得最优控制量,而考虑侧风配平的重定位技术尚未有文献涉及。针对此问题,本文对模拟器的侧风配平重定位技术进行了研究,分析了模拟器重定位功能需求过程,阐述了侧风配平的实现过程,提出了应用基于改进的最速下降法进行侧风配平的优化计算,并在某民用飞机工程模拟器上进行了仿真验证。
1 模拟器架构
工程模拟器是一个高度复杂的系统,既包括由大量数学仿真模型来模拟的“虚拟系统”,也包括飞机的部分真实系统、器件或者仿真件。工程模拟器主要由驾驶舱结构与驾驶舱设备仿真系统、主飞行仿真系统、飞控仿真系统、航电仿真系统、视景系统、六自由度运动系统、声音仿真系统、综合控制台系统、硬件接口系统、计算机实时仿真系统、环境与支持系统等分系统组成,通过建模与仿真技术,为工程师和飞行员提供了具有运动感觉和高逼真度模拟飞行环境的设计试验平台。工程模拟器架构如图1所示。
2 数学模型
2.1 运动方程模块
在飞行仿真系统中,该模块首先计算机体轴上的合外力和合力矩,然后计算沿机体轴的线加速度和角加速度,并应用积分产生飞机的合成速度。把风和紊流扰动速度加到机体轴线速度上,用来计算飞行轨迹参数。把机体轴角速度分解到气流轴上用来计算飞机迎角、侧滑角及其变化率,以提供给气动系数模块使用。把角速度分解到地面坐标系上,应用积分计算3个欧拉角,为视景、仪表等系统提供飞机姿态参数[9]。
2.2 风模型
风模型是工程模拟器的重要组成部分。通过建立风切变、紊流等风模型模拟复杂的气象环境,可为模拟器提供逼真的风场环境模拟。
2.2.1 平均风计算
平均风速可由飞机位置到预期着陆点位置的线性插值得到;如果飞机位置在特定风场之外,不再使用外推法。相反,则使用给定位置的数据。
2.2.2 紊流计算
3 重定位技术
3.1 重定位功能需求
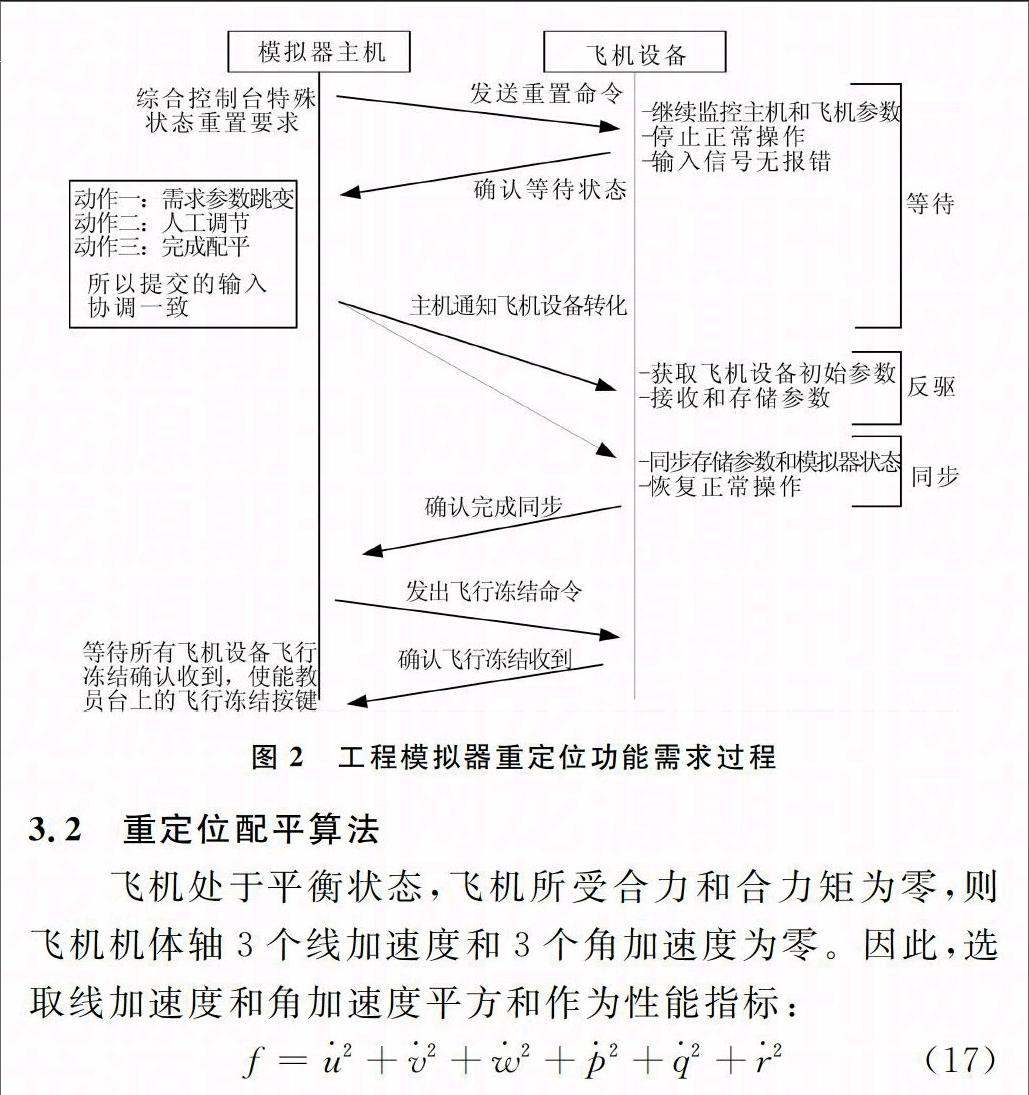
特殊状态重置是想定设置的一种,用来满足特定的训练或试验要求以选定特定的飞行状态,也可用来快速实现模拟器鉴定自动测试时的初始状态。在模拟器试验过程中,工程人员需设置大量的不同飞行科目试验状态点开展试验,如起飞、着陆、配平、横航向静稳定性、动稳定性、纵向操纵效能等。为了提高工程模拟器试验效率及对试验结果进行高效处理,需在工程模拟器上实现任意点设置完成后飞机可自动配平的功能。该功能要求在综合控制台设置重量、重心、高度、速度后,根据当时飞机起落架收放位置、襟缝翼位置等相关参数,自动解算飞机各配平模式所需要的迎角、侧滑角、油门杆位置以及操纵面(升降舵、方向舵、副翼)偏角等的配平位置,使飞机能够在设置完成后进入所要求的稳定配平状态,使飞机所受合力和合力矩为零。在配平的基础上,才可以加控制信号完成各种飞行功能。工程模拟器重定位功能需求过程如图2所示。
3.2 重定位配平算法
飞机处于平衡状态,飞机所受合力和合力矩为零,则飞机机体轴3个线加速度和3个角加速度为零。因此,选取线加速度和角加速度平方和作为性能指标:
在待求的状态变量中根据平衡状态类型来控制变量,在侧风配平重定位设计时,选取迎角、侧滑角、滚转角、操纵面(升降舵、方向舵、副翼)偏角、发动机油门位置作为待优化的控制变量。补充适当的辅助方程后,性能指标f成为控制变量的函数,即给定一组控制变量后,根据运动方程可唯一求解性能指标f值。在性能指标f取最小值时对应的最优控制量为所求的飞机平衡点状态量,其它状态变量可根据运动学及几何关系求得。
3.3 重定位优化计算算法
解上述非线性方程组有多种方法,例如Newton迭代法、近似Newton法、遗传算法、混合遗传算法粒子群优化算法等。但这些算法考虑过于全面,程序设计较为复杂,计算量大。本文考虑计算量、收敛速度、工程模拟器上优化算法程序实现难易程度等因素,选取曲英杰等[10]提出的改进的最速下降算法。该算法对最速下降法作了改进,使其收敛速度由一阶提高到二阶,其原理是先将初始向量x(0)用最速下降法迭代2m步,得到2m+1个向量S(0),S(1),···S(2m),然后应用向量ε算法将2m+1个向量加以改进,得到一个新的向量x(1);然后再将x(1)作为新的初始近似向量,用最速下降法迭代2m,再将得到的向量组用向量ε算法加以改进,得到新的向量x(2);以此类推,就得到一向量序列x(k)。
3.4 侧风配平重定位
3.4.1 侧风配平模式要求
设置飞机的总重量、重心、高度、速度、风向、风速、起落架和襟缝翼状态,配平飞机的推力、迎角、侧滑角、水平安定面角度、副翼角度,设置结束后,飞机可在设置状态下配平,飞行解冻后,飞机瞬态以设置的迎角、侧滑角、定高度、定速度直线平飞。
3.4.2 侧风配平过程
侧风配平过程如下:①根据各配平模式的要求,将试验状态点的重量、重心、高度、速度参数设置成脚本文件,根据预先设置好的试验构型文件,在试验时通过综合控制台选择脚本文件中的试验构型,实现自动加载试验状态点的设置;②实现飞行仿真系统的配平算法:能够根据设置的高度、速度、重量、重心、襟缝翼位置、减速板位置、起落架位置等参数,解算配平状态的迎角、所需水平安定面角度、所需发动机推力、副翼角度和方向舵角度等参数;③实现水平安定面的配平驱动:能够根据配平计算的所需水平安定面角度,在短时间内驱动水平安定面的动作,到达所需要的位置; ④实现油门杆的配平驱动:能够根据配平计算的所需推力,短时间内将油门杆驱动到合适位置,使发动机提供满足阈值要求的所需推力;⑤实现副翼和方向舵的配平驱动;能够根据横航向配平所解算出的副翼和方向舵,短时间内驱动方向舵和操纵杆到所需位置;⑥实现配平过程的逻辑控制,能够正确响应配平的逻辑,只有在配平完成后才能实现“飞行解冻”,并能够在解冻后配平位置基础上实现人工调节水平安定面的功能,解冻后在此配平基础上实现人工调节油门杆进而控制推力的功能。
侧风配平具体实现流程如图3所示。
4 计算结果仿真及分析
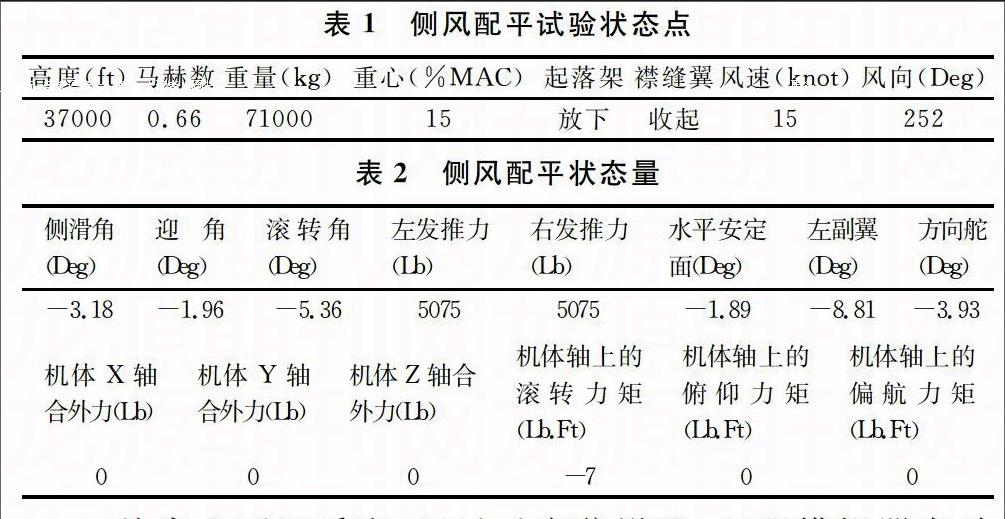
本文以某型飞机为例,计算了侧风状态下的飞机平衡状态。为了使评估试验进行得更为充分,可考虑选择不同的飞机高度、重量、重心、速度、起落架和襟翼位置以及飞行阶段的试验点,本次试验分析的试验状态点(右侧风、起落架放下、襟缝翼收上)如表1所示,
计算所得配平状态量如表2所示。
从表2可以看出,通过重定位设置,工程模拟器自动解算出飞机侧风配平模式所需要的迎角、侧滑角、滚转角、发动机推力以及操纵面(升降舵、方向舵、副翼)偏角的配平位置,此时飞机所受合力和合力矩均为零,表明飞机在重定位设置完成后进入要求的稳定配平状态,在配平的基础上,飞行解冻后飞行员施加试验任务单中要求的飞行员动作以完成相应的试验。
本文给出了一个试验状态点的配平,在试验过程中大量的试验状态点重定位计算表明,采用改进的最速下降法较为简单、计算量少、收敛速度快、稳定性好、易于工程实现,可以实现全飞行包线内的配平。
5 结语
本文对模拟器的侧风配平重定位技术进行了研究,采用改进的最速下降法优化计算飞机平衡点状态量,以及配平实现过程,并在某民用飞机工程模拟器上进行了仿真验证。仿真结果表明,采用改进的最速下降法较为简单、计算量少、收敛速度快、稳定性好、易于工程实现,可以实现全飞行包线内的配平。配平实现过程具备较强的可操作性,具有重要的工程应用价值,为其它模拟器重定位技术提供了重要参考。
参考文献参考文献:
[1]鲁可,钱俊铭,曹艳玲,等.无人战斗机非线性模型及配平方法[J].青岛科技大学学报,2012,33(4): 422426.
[2]沈宏良,刘昶.飞机平衡状态的优化计算方法[J].飞行力学,2001,19(4): 1518.
[3]刘艳,高正红.基于飞行性能最优的多操纵面飞机配平研究[J].飞行力学,2009,27(5): 1720.
[4]李洪冬,张民,陈欣.基于算法的飞机平衡状态求解[J].计算机仿真,2011,28(8): 5660.
[5]李超,王江云,韩亮.基于Matlab的某型固定翼飞行器飞行仿真系统开发[J].系统仿真学报,2013,25(8): 17721777.
[6]王海涛,高金源.基于混合遗传算法求解飞机平衡状态[J].航空学报,2005,26(4): 470475.
[7]张剑.基于MATLAB编程实现的民用喷气飞机配平计算软件[J].软件导刊,2013,12(4): 115117.
[8]徐南波.民用飞机单发失效情况下横航向配平研究[J].科技信息,2013,18(2): 480.
[9]王行仁.飞行实时仿真系统及技术[M].北京: 北京航空航天大学出版社,1998.
[10]曲英杰,宫献军,孙光亮.工程优化中最速下降法的加速技巧[J].山东工业大学学报,1996,26(4): 495498.
责任编辑(责任编辑:孙 娟)
英文摘要Abstract:This paper analyzes functional requirement procedure of reposition,studies realization process of crosswind trim for engineering simulator and presents a general optimization method based on steepest descent method to solve state of crosswind trim. This method has applied to an engineering simulator of civil aircraft. The result shows that modified steepest descent method is correct and effective,which has a low amount of computation,fast rate of convergence,and good stability. It can be easily realized in a project,and can obtain trim state in full flight envelope. This conclusion is achievable and of important engineering value,and provides important reference for reposition technical of engineering simulator.
英文关键词Key Words: Engineering Simulator;Reposition;Crosswind Trim;Steepest Descent Method;Optimization
