关于H-联图的拉普拉斯特征值

娄源源， 吴宝丰

(上海理工大学理学院，上海 200093)

关于H-联图的拉普拉斯特征值

娄源源， 吴宝丰

(上海理工大学理学院，上海 200093)

H-联图是在不交图G1，G2，…，Gk的基础上，对于H中的任意两点i，j，若ij∈E(H)，则将Gi的每一点与Gj的每一点相连所得到的图，其中，H的顶点集为{1，2，…，k}.特别地，{G1，G2}的P2-联图就是普通联图G1∨G2.本文研究了H-联图的拉普拉斯特征多项式，给出了H-联图的拉普拉斯谱与图G1，G2，…，Gk以及基图H的拉普拉斯谱之间的关系.进一步研究了基图分别为完全图、完全二部图时的H-联图，给出了Kk-联图和Ks，t-联图的拉普拉斯谱以及相应的特征多项式.另外，证明了当基图H是完全图、完全二部图或阶数小于等于4的图(除P4外)时，L-整图{G1，G2，…，Gk}的H-联图也是L-整的.

H-联图；拉普拉斯特征值；整图

1 基本概念

图G的邻接矩阵定义为A(G)=(aij)，其中当ij∈E(G)时，aij=1；否则，aij=0.图G的拉普拉斯矩阵定义为L(G)=D(G)-A(G)，其中D(G)=diag(d1，d2，…，dn)为G的度对角矩阵.

考虑方阵M，M的特征多项式表示为P(M，x)= det(x I-M)，M的特征值即为P(M，x)的根，其中，0特征值的重数称为M的零度.M的谱Spec(M)是由M的特征值组成的多重集合，用符号a+ Spec(M)(或aSpec(M))表示Spec(M)中的每一个元素加上a(或乘以a).特别地，图G的拉普拉斯特征多项式记为，图G的拉普拉斯谱记为SpecL(G)(即L(G)的谱).若L(G)的特征值全为整数，则称图G是L-整的.

定义1[1-2]设图H的顶点集为{1，2，…，k}，Gi为ni阶图(i=1，2，…，k)，则{G1，G2，…，Gk}的H-联图，记作∨H{G1，G2，…，Gk}，它是在G1，G2，…，Gk的基础上，对于H中的任意两点i，j，若ij∈E(H)，则将Gi的每一点与Gj的每一点相连所得到的图.图H称为联图∨H{G1，G2，…，Gk}的基图.

特别地，当基图H=P2时，P2-联图就是普通的联图，即∨P2{G1，G2}=G1∨G2.当所有Gi(i= 1，2，…，k)相同，均为G时，为方便起见，用符号H⊙G来代替∨H{G，G，…，G}，即H的每一点都被“吹大”成G后所得到的图.

联图的特征多项式(或谱)已被广泛研究，如文献[1]较早地研究了它的邻接特征多项式，文献[2]研究了它的邻接谱和拉普拉斯谱.另外，P2-联图在图的标号理论研究中也引起了高度关注.

2 H-联图的拉普拉斯特征多项式

定义2 设图H的顶点集为{1，2，…，k}，Gi为ni阶图(i=1，2，…，k)，考虑H-联图∨H{G1，G2，…，Gk}，定义:

由定义可知，Lπ的行和均为0，从而0是它的一个特征值，Lπ是奇异矩阵.不难验证，对于H-联图G=∨H{G1，G2，…，Gk}，它在划分π:V(G)= V(G1)∪·…∪·V(Gk)下的L-因子矩阵就是L(G)基于该划分的商矩阵.

引理2 设图H的顶点集为{1，2，…，k}，Gi为ni阶图(i=1，2，…，k)，若G=∨H{G1，G2，…，Gk}，Lπ为G的关于划分π:V(G)=V(G1)∪·…∪·V(Gk)的L-因子矩阵，CL(H)同定义2，则矩阵Lπ与CL(H)相似.

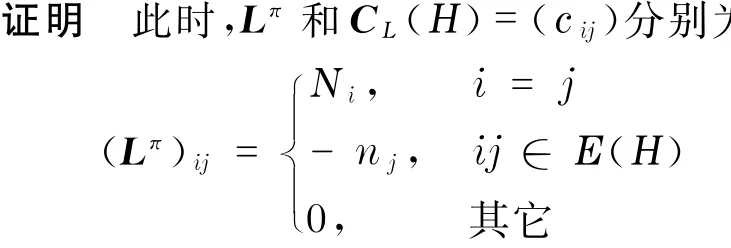
3 L-整图

整图的谱完全由整数构成，哪些图是整图呢?该问题由Harary等[6]于1973年针对邻接谱提出，同时指出了此类问题具有一定的难度.整图的数量是无限的，而且在各类图集中都可能存在，但是，它们仍然是非常稀少的，并且难以找到.例如，最大度固定的整图，其数量是相当有限的.通常是利用已知的整图通过图的运算来构造新的整图[6-8].对于拉普拉斯谱，完全图、完全二部图都是L-整的，所以，

引理4 设H为k阶树，则H是L-整图，当且仅当H为星图K1，k-1.

证明 星图是L-整的，所以，充分性显然，现证必要性.

当k=1，2或3时，此时的树都是唯一的，即星图，结论成立.

当k≥4时，若H≠K1，k-1，则H的直径d≥3，由引理3可知

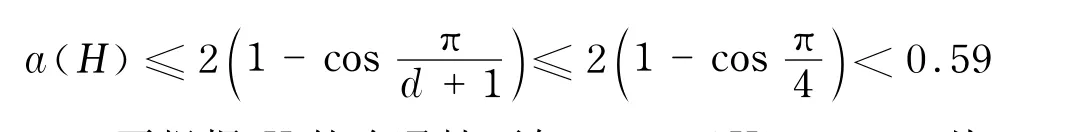
再根据H的连通性可知，0＜a(H)＜0.59，从而a(H)不是整数，即L(H)的第二小特征值不是整数.这与H是L-整图矛盾，所以，H=K1，k-1.

定理7 设H为k阶树，G为L-整图，则H⊙G是L-整的，当且仅当H=K1，k-1.

证明 由推论6和引理4可知结论成立.

[1] Schwenk A J.Computing the characteristic polynomialof a graph[J].Lecture Notes in Mathematics，1974，406:153-172.

[2] Cardoso D M，de Freitas M A A，Martins E A，et al. Spectra of graphs obtained by a generalization of the join graph operation[J].Discrete Mathematics，2013，313(5):733-741.

[3] Wang J F，Belardob F.A note on the signless Laplacian eigenvalues of graphs[J].Linear Algebra and Its Applications，2011，435(10):2585-2590.

[4] Cvetkovic′D，Rowlinson P，Simic′S.An introduction to the theory of graph spectra[M].New York:Cambridge University Press，2010.

[5] Cardoso D M，Delorme C，Rama P.Laplacian eigenvectors and eigenvalues and almost equitable partitions [J].European Journal of Combinatorics，2007，28(3):

[6] Harary F，Schwenk A J.Which graphs have integral spectra?[J].Lecture Notes in Mathematics，1974，406:45-51.

[7] Grone R，Merris R.The Laplacian spectrum of a graph II[J].SIAM Journal on Discrete Mathernatics，1994，7 (2):221-229.

[8] 陈永玲，何常香.二部双圈图的拉普拉斯系数[J].上海理工大学学报，2012，34(5):481-486.

[9] Grone R，Merris R，Sunder V S.The Laplacian spectrum of a graph[J].SIAM Journal on Matrix Analysis and Applications，1990，11(2):218-238.

[10] 沈富强，吴宝丰.最小Q-特征值为给定整数的一类图[J].上海理工大学学报，2014，36(5):425-428.

(编辑:石 瑛)

Laplacian Eigenvalues on the H-Join Graphs

LOU Yuanyuan， WUBaofeng
(College of Science，University of Shanghai for Science and Technology，Shanghai 200093，China)

The H-join graph is obtained on the basis of disjoint graphs G1，G2，…，Gkand by joining each vertex of Gito each vertex of Gjwhenever i is adjacent to j in H.In particular，the P2-join graphs{G1，G2}is the ordinary join graph G1∨G2.The Laplacian characteristic polynomial of the H-join graph was studied，and the relations between the Laplacian spectrum of the H-join graph and those of the graphs Gi(i=1，2，…，k)and H were obtained，especially for the Kk-join graph and Ks，t-join graph.Moreover，the fact was proven that the H-join of Laplacian integral graphs{G1，G2，…，Gk}is also Laplacian integral when H is the complete graph，the complete bipartite graph or the graph of order not greater than 4 except for P4.

H-join graph；Laplacian eigenvalue；integral graph

O 157.5

A

2013-12-18

国家自然科学基金资助项目(11301340，11201303)；上海市自然科学基金资助项目(12ZR1420300)第一作者:娄源源(1988-)，男，硕士研究生.研究方向:代数图论.E-mail:xylouyuanyuan@163.com

吴宝丰(1978-)，男，讲师.研究方向:代数图论.E-mail:baufern@usst.edu.cn