基于小波的回归-GARCH模型及其在外汇储备中的应用

肖云湘, 李星野

(上海理工大学管理学院,上海 200093)

基于小波的回归-GARCH模型及其在外汇储备中的应用

肖云湘, 李星野

(上海理工大学管理学院,上海 200093)

结合小波变换、多项式回归和GARCH模型对中国的外汇储备进行分析及预测.首先利用db4小波对数据进行去噪处理,并对去噪后的数据建立多项式回归模型.由于去噪后的数据与回归模型之间存在残差,且残差具有自回归条件异方差效应,故对该残差建立GARCH模型.然后将回归模型和GARCH模型进行线性叠加,从而得到基于小波分析的回归-GARCH模型.最后将预测值与实际值进行拟合,发现拟合效果较好.充分证明了小波变换、多项式回归和GARCH模型相结合的方法在处理外汇储备这类具有明显增长趋势的非平稳时间序列时,具有明显的优越性,是一项有用的分析预测工具.

小波;时间序列;多项式回归;GARCH模型;外汇储备

信号处理已广泛应用于经济和金融等方面,其中,信号预测,即时间序列预测,在(宏观)经济、统计、实证金融等领域中非常受欢迎.外汇储备,又称为外汇存底,是一个国家当局持有并可以随时兑换外国货币的资产,包括现钞、黄金、国外有价证券等.持有外汇储备是调节国际收支、稳定货币汇率、实现内外平衡的重要手段.中国的外汇储备主要由四部分组成:一是巨额贸易顺差;二是外国直接投资净流入的大幅增加;三是外国贷款的持续增多;四是对人民币升值预期导致的“热钱”流入.在肯定外汇储备增长的正面效应时,其过度增长也存在潜在的负面影响.例如,外汇储备投资欧美国债就可能面临以下风险[1]:保值增值功能的相对弱化、汇率风险、宽松政策下潜在的通货膨胀风险.简单地说,持有过多外汇储备,可能因外币汇率贬值而遭受损失,还要考虑机会成本问题.为了能够更确切地把握我国外汇储备的增长趋势,本文对1993年以来的外汇储备数据进行了建模,以此来预测短期内我国外汇储备的增长趋势.

由于许多经济和金融时间序列都具有时变性,所以小波成为分析时间序列的好方法[2].尽管小波适用于很多领域,但其主要应用热点是经济和金融的多元研究,研究方向有密度估计、时间尺度分解、时间序列的相互依存关系识别和预测等.

外汇储备数据中都或多或少地引入了噪声,使预测精度受到了影响,对数据进行去噪是解决该问题的方法之一.以往的去噪方法都是基于Fourier变换进行的,基于小波变换的去噪技术与传统的去噪方法相比,能够在有效去除信号中噪声的同时,适当保留信号的高频部分,这是Fourier变换所不可比拟的.根据我国外汇储备序列的特点,研究发现该序列适合应用小波分析、多项式回归和GARCH模型相结合的预测方法.

1 研究现状

截至2006年底,中国外汇储备的规模突破万亿美元大关,已经达到了10 663亿美元,成为世界第一大外汇储备国.中国外汇储备的持续高速增长已经引起了国内外学者的关注,不少学者从外汇储备额的预测方面出发,分析我国外汇储备的走势.

最新对我国外汇储备作出预测的是宋国青教授[3],他在2005年9月就明确指出:“按照目前势头,(我国外汇储备)不久超过2万亿美元是铁定的,而其可能见顶于3万亿美元.”但没有提供具体的预测方法.2006年,卢峰[4]采用幂函数、线性函数、指数函数三种方法,拟合和预测我国的外汇储备.但这三种方法对2020年外汇储备的长期预测相差甚大,实际效果不太好.第一种预测方法增长趋势比较均衡,推测到2020年我国外汇储备应约为1.1万亿美元,这显然与事实不符;第二种预测方法采取2002年以来外汇储备实际增长的线性趋势,到2020年也将达到3.5万亿美元上下;第三种预测方法是极端假设继续2002年以来指数增长趋势,5年就会达到近5万亿美元规模.无论第二、三种预测方法的结果如何,其研究数据均是2002—2005年的外汇储备额,依据时间太短,而预测的时间又太长,显然不恰当.2007年,张曙光等[5]进一步提出了四种预测我国外汇储备的方法,选择1994—2005年间的外汇储备额.第一种方法是指数增长法估算,采用指数函数对外汇储备变动进行回归方程外推,得到2010年中国外汇储备达到19 869.8亿美元;第二种方法是组成部分加总法测算,根据国际收支平衡表,有恒等式:经常账户余额+资本账户余额=储备资产变动+净误差与遗漏,该方法分别估算出每一组成部分,预测2010年外汇储备约为2.5万亿美元;第三种方法是年平均增长率估算,预计2010年外汇储备将达到2.88万亿美元;第四种方法是将以上三种方法的估计取平均,得到2010年外汇储备将达到2万亿美元.之后也有不少学者提出对我国外汇储备额趋势进行预测的方法,但这些研究方法均没有考虑到外界(即噪声)对外汇储备的影响.

2 理论模型

2.1 小波变换理论

小波变换[6]是通过伸缩和平移等运算对函数或信号进行多尺度的细化分析,利用多分辨率分析得到更多信息[7].

设ψ(t)∈L2(ℝ),其傅立叶变换为^ψ(ω),当^ψ(ω)满足允许条件(完全重构条件或恒等分辨条件)

式中,a为伸缩因子,a≠0;b为平移因子.对于任意的函数f(t)∈L2(ℝ),其连续小波变换为

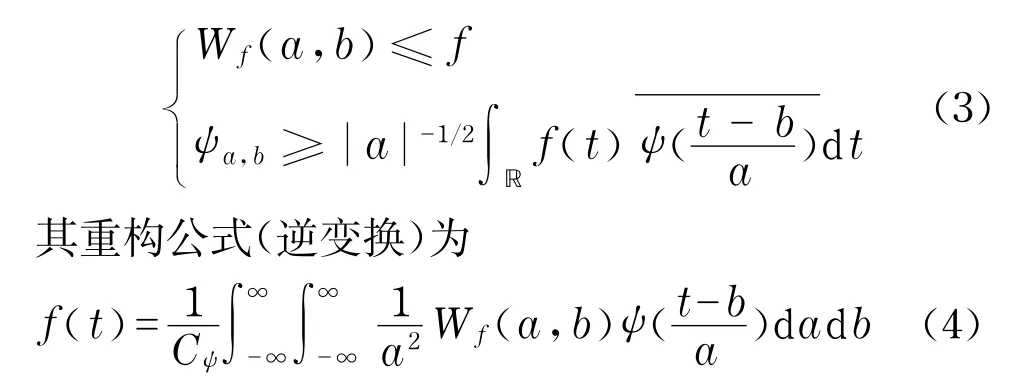
Daubechies小波系是法国学者Daubechies从两尺度方程系数{hk}出发设计出来的离散正交小波的总称.一般简写为db N,N是小波的序号,小波函数和尺度函数的支撑区为2N-1,小波函数的消失矩为N.

从数学上看,小波去噪问题的本质是函数的非线性逼近问题;从信号学角度看,小波去噪属于信号的滤波问题.

首先对信号进行小波分解,这需要选择适当的小波函数并确定其分解层次(N),通常噪声部分包含在高频中.然后对小波分解的高频系数进行门限阈值量化处理,根据小波分解的第N层低频系数和经过量化后的1～N层高频系数进行小波重构,达到消除噪声的目的.

关键是如何选择阈值和如何进行门限阈值处理,在某种程度上,它关系到信号去噪的质量.在对小波系数作门限阈值处理操作时,可以使用软阈值处理方法或硬阈值处理方法.一般来说,硬阈值比软阈值处理后的信号更粗糙一些[8].

2.2 GARCH模型

Bolloerselev[9]提出的广义自回归条件异方差(GARCH)模型是对Engle提出的自回归条件异方差(ARCH)模型的拓展,有均值方程和方差方程两个方程,能更加有效地捕捉金融时间序列条件方差的动态特征,也能较好地描述金融时间序列的尖峰厚尾性[10].

把式(5)中的t替换为t+1,就可以得到领先一步的预测.由此可知,GARCH模型描述的是均方误差的平均大小随时间的变动.虽然GARCH模型具有良好的预测能力,但所获得的结果仍依据时间段的不同而有所不同,归根结底还取决于时间序列上的波动结构.

可以准确预测的方法至今仍然没有被发现,每种方法都有自己的优点,而且也从统计学上证明了这些方法获得的良好结果.本文预测模型将不仅仅是象许多计量经济模型那样直接对原始数据进行预测,而是应用于小波去噪后的序列,在序列建模时,可以提高预测精度.

本文所提出的模型如图1所示,每个模块的相应描述在第三部分给出.

图1 预测模型Fig.1 Prediction model

3 实证分析

选取1993年1月至2012年12月间我国外汇储备的月度数据(数据来源于国家外汇管理局网站),共240个数据,如图2所示.

图2 1993年1月至2012年12月的外汇储备Fig.2 Foreign exchange reserves from Jan.1993 to Dec.2012

3.1 小波去噪

db N小波是有限紧支撑正交小波,具有正交性和较好的降噪性[11].这个小波函数的消失矩N越大,小波函数越光滑,支撑长度越长,但小波变换的计算将会增加延长.因此,选取db4小波来分析问题.由于预测结果是从小波分解序列的去噪结果得到,且分解过程中存在误差,分解的层数越多,误差就越大,越不利于预测模型.经过具体计算,本文分解的尺度为3.图3为用默认阈值去噪方法处理后的外汇储备.可见,默认阈值去噪在除去大部分噪声的同时,很好地保留了原始数据的波动趋势,说明去噪是合适的.

图3 默认阈值去噪后的外汇储备Fig.3 Foreign exchange reserves afterdenoising of default threshold

3.2 建立多项式回归模型

由图3可以看出,去噪后的序列适合建立自变量为时间,因变量为外汇储备的二次多项式.

在一般情况下,不能要求近似曲线严格地通过所有数据点,亦即不能要求所有拟合曲线函数在所有自变量处的偏差(即残差)都严格地趋于零.为了方便计算、分析与应用,较多根据“偏差平方和最小”(即最小二乘法)的原则,来选取拟合曲线.

用最小二乘法所得的二次方程为

式中,R2为复可决系数,是模型拟合优度的指标, R2越接近于1,模型拟合越好;F,DW为检验值,分别用于检验方程的显著性和序列的自相关.从回归估计的结果可以看出,拟合度较好.去噪序列与回归序列的对比如图4所示.

图4 去噪序列与回归序列的对比Fig.4 Denoised series vs regression series

3.3 建立GARCH模型

建立GARCH模型的前提是数据平稳.所以,在对去噪序列与多项式的残差序列Zt(图5)进行建模前,首先要确定其平稳性.

图5 残差序列Fig.5 Residual series

使用ADF检验方法对残差序列Zt的平稳性进行检验.换而言之,当计算得到的t统计量的值小于临界值时,拒绝原假设(即否定存在单位根).表1结果显示,t统计量的值大于在1%,5%和10%显著性水平下的临界值,该残差序列存在单位根,是非平稳时间序列,其中P为t对应的概率值.

表1 残差序列的ADF检验Tab.1 ADF test of residual series

如要构造GARCH模型,就得对该非平稳序列进行平稳化处理,然后才能对其进行预测.该残差序列没有指数趋势,通过差分就可以消除其线性趋势.即对Zt做差分

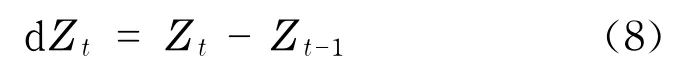
经过试验,对该序列进行两次差分后,其ADF检验的结果如表2所示.在1%,5%和10%显著性水平下,单位根检验的临界值分别为-3.459 494, -2.874 258,-2.573 625,均大于-8.137 927,拒绝原假设,即认为是平稳序列.

表2 残差序列二次差分的ADF检验Tab.2 ADF test of 2nddifference residual series

用ARCH-LM方法检验Zt的残差序列发现其存在高阶ARCH效应,运用GARCH模型,能较好地消除残差序列中的条件异方差.经过多次试验,根据AIC最小的原则,对Zt建立的GARCH模型为

3.4 线性叠加

将用多项式模型得到的序列和用GARCH模型得到的序列进行线性叠加,就可以得到我国外汇储备的95%置信度的预测区间,如图6所示.

图6 实际值与预测值Fig.6 Actual values vs predicted values

图7为2012年1—12月的实际值与预测值.可以发现,模拟效果较好,即本文提出的算法对结果有积极的影响.

图7 2012年1—12月的实际值与预测值Fig.7 Actual values vs predicted values from Jan.to Dec.in 2012

4 结 论

给出了结合小波变换、多项式回归和GARCH模型来处理我国外汇储备序列的方法.该方法在处理外汇储备这类有明显增长趋势的非平稳时间序列时,具有明显的优越性,是一项有用的分析预测工具.根据该方法预测可知,如果政府没有采取一系列的措施,我国的外汇储备2013年中期超越3.5万亿美元,继续保持全球第一,这么庞大的外汇储备远远超过正常所需.长期的国际收支不平衡与资本顺差累积可能会引起许多金融问题,使我国在一定程度上丧失货币政策操作的主动权,长期处于减轻人民币升值与抑制通货膨胀的两难境地,这需要政府积极地采取有效的措施,鼓励合理的资本流出.

[1] 江凯.外汇储备投资欧美国债的动因、风险及建议[J].金融与经济,2012,32(7):29-31.

[2] Kim S,In F H.The relationship between financial variables and real economic activity:evidence from spectral and wavelet analyses[J].Studies in Nonlinear Dynamics and Econometrics,2003,7(4):4.

[3] http:∥wenzhu.blog.hexun.com/91071422_d.html.宋国青.全球通大河论坛讲演[N].2005-9-24.

[4] 卢峰.我国国际收支结构变动及其人民币汇率影响——人民币实际汇率长期走势研究之四[R].北京:北京大学中国经济研究中心,2006.

[5] 张曙光,张斌.外汇储备持续积累的经济后果[J].经济研究,2007(4):18-29.

[6] Glosten L R,Jagannathan R,Runkle D E.On the relation between expected value and the volatility of the nominal excess return on stocks[J].The Journal of Finance,1993,48(5):1779-1801.

[7] 马琳琳,李星野.基于多分辨率分析和改进离散余弦变换的音频水印算法[J].上海理工大学学报,2007, 29(5):417-422.

[8] 王彦青,魏连鑫.一种改进的小波阈值去噪方法[J].上海理工大学学报,2011,33(4):405-408.

[9] 高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2009.

[10] 陈潇,杨恩.中美股市杠杆效应与波动溢出效应——基于GARCH模型的实证研究[J].财经科学,2011, 277(4):17-24.

[11] Yousefi S,Weinreich I,Reinarz D.Wavelet-based prediction of oil prices[J].Chaos Solitons&Fractals, 2005,25(2):265-275.

(编辑:董 伟)

Wavelet-Based Regression-GARCH Model and Its Application in Foreign Exchange Reserves

XIAOYunxiang, LIXingye
(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

The wavelet transform and the polynomial regression were combined with the GARCH model to analyze and forecast China’s foreign exchange reserve.The data were de-noised by the db4 wavelet to establish polynomial regression model.Seeing that between the residuals of the denoised data and the regression model there exist the auto regressive conditional heteroskedasticity (ARCH)effects,the GARCH model was created.Linear superposing the regression model and GARCH model,a regression-GARCH based on wavelet analysis was proposed.Comparing the predicted value and the actual value,it is found that the result in the paper is quite well.In other words,the method presented has obvious advantages and it’s a useful predictive analysis tool in dealing with the non-stationary time series which has obvious growth trend just like foreign exchange reserves.

wavelet;time series;polynomial regression;GARCH model;foreign exchange reserve

F 830

A

1007-6735(2015)01-0018-05

10.13255/j.cnki.jusst.2015.01.004

2013-10-14

国家自然科学基金资助项目(71071098);上海市一流学科建设资助项目(XTKX2012)

肖云湘(1990-),女,硕士研究生.研究方向:复杂经济系统分析.E-mail:maiuth@163.com

李星野(1958-),男,教授.研究方向:信号分析与识别、复杂经济系统分析等.E-mail:lixingye@tsinghua.org.cn