全钢轮胎仿形缠绕过程的模型预测控制
2015-06-23陈乐庚
陶 越,陈乐庚
(桂林电子科技大学电子工程与自动化学院,广西桂林 541004)
全钢轮胎仿形缠绕过程的模型预测控制
陶 越,陈乐庚
(桂林电子科技大学电子工程与自动化学院,广西桂林 541004)
为提高轮胎仿形缠绕控制系统的稳定性及控制的快速性,根据缠绕系统数学模型,提出噪声不确定系统的基于动态输出反馈预测控制算法。通过缠绕模型的估计状态与误差集合,建立误差离线数据库;在线时,估计误差在辅助优化中实时更新,计算实时控制器与预测控制器。实验结果表明,改进后的控制方法可行、有效,大幅提升了控制的快速性,并且误差可控制在稳定的范围内,适合实际生产。
仿形缠绕;预测控制;数学模型;动态输出反馈
轮胎缠绕是国内外采用的一种胎面成型方式[1],主要应用于全钢工程载重子午线轮胎的成型。由于一些特定的场合,外界环境的恶劣因素影响轮胎的使用寿命,需要轮胎结构稳定,载重、抗压能力强[2],对其生产制造过程需严格把关,尤其胎面缠绕贴合过程要求更高。目前轮胎的工业生产,还没有具体的仿形缠绕模型,很多专家设计的模型均基于在线辨识。由于计算机运算速度的限制及大功率环境下干扰信号的存在,实际运用均有很强的滞后性,模型辨识速度跟不上生产速度,在线及离线优化算法急需大幅提高技术水准[3]。
传统的基于模型误差修正的广义预测控制算法[4]用于全钢轮胎仿形缠绕控制系统的实际效果并不理想;常规的在线优化算法,实时数据采集、分析及计算耗时巨大[5-6],限制了在工业快速实时控制中的应用。基于BP网络的GPC算法收敛速度比较慢,难以实时控制快速模型,且未充分考虑有界状态噪声和量测噪声[1],无法确保预测控制系统的稳定,真实状态的界是动态不确定的[7]。为此,提出一种噪声不确定系统的基于动态输出反馈的预测控制算法,以提高轮胎胎面生产的工艺控制水平。
1 动态输出反馈预测控制算法及在线更新估计误差
将在线优化控制转变成离线优化控制问题,可降低在线计算量[5],提高系统响应的快速性。将一系列控制问题及优化策略离线求解,设定新型嵌套渐进稳定不变集,在控制策略中实时搜索最优的渐进稳定不变集,采用插值法智能计算在线控制器参数,同时,引入系统抗噪因子,考虑系统状态的估计误差、估计误差约束、估计状态及系统输出状态。改进辅助优化策略,为增强系统稳定性与控制性能[3],将估计误差在辅助优化中实时更新,离线选择控制对象的状态,拟合估计状态与误差集合、预测控制器的参数及吸引域。在线时,实时智能搜索系统的运行状态,选择稳定的最优控制策略[5,8]。
计算离线控制器参数,以nφ维状态空间分布在原点周围的有限数的离散点为主要选取的估计状态集合,根据估计误差稳定集合的界确定不同的实际状态的界,并假设实际状态分布在选定估计状态集合的周围。将正交分解的状态空间交叉点设置为估计状态,Γk,k∈{1,2,…,nφ}表示每一维正交分割区域在横坐标上的投影。这种模式将获得(2NΩ)个分割包及(2NΩ+1)个交叉点,把这些交叉点设定为各种估计状态,每个分割包用符号ζτ表示,分割包的序列号用符号τ∈{1,2,…,(2NΩ)}表示,对应分割包的顶点集合用符号V(ζτ)∈{,…,}表示。
令NΩ=3,nφ=2,图1为对分割包ζτ等体积正交分割,以分割包的各个顶点为估计状态,并参考估计误差列表,定义真实状态的界。定义扩展状态如图2所示,根据估计误差集合及顶点,虚线内部区域表示相应的综合预测扩展状态。定义嵌套集合为:

其中:ηn∈(0,1];ηn≤ηn+1;n∈{1,2,…,NΩ}。

图1 对分割胞的正交分割Fig.1 Quadrature divider for dividing cells
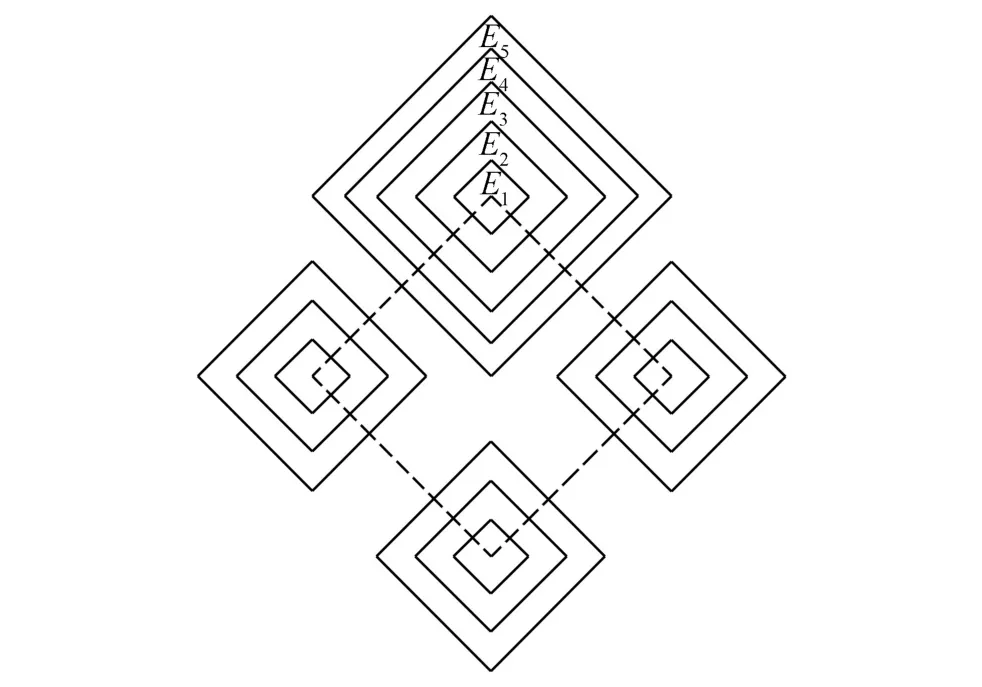
图2 定义扩展状态Fig.2 The definition of an extended state
将其设定为估计误差集合,En中任一集合为外凸多面体且该多面体(多面体顶点数为个)的顶点可描述为ηn,c∈{1,2,…,2Ω},Sc的对角元素为-1或1,其余为0。当ηn=1时,估计误差集合En取最大,将估计状态与估计误差集合进行智能组合,全局寻优预测控制指标,离线预测最优控制策略对应的吸引域和控制器参数。

i时刻,若e(i)∈~E(i)∈~E◇(i),根据关系
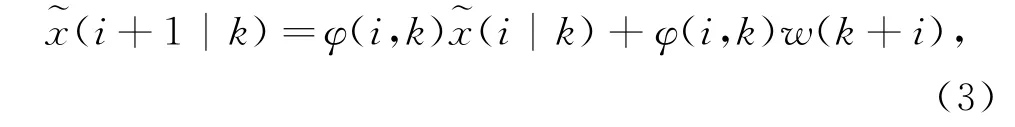
若∀i≥0,有~x(0|k)=~x(k),则存在下列估计误差:
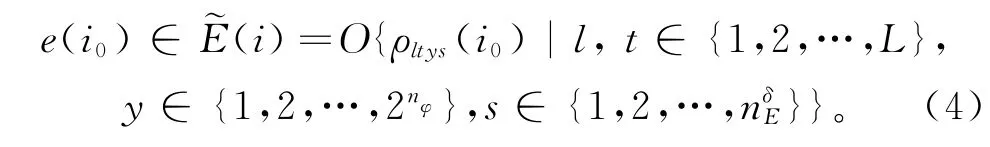
其中ρltys(i0)为控制误差期望的变量。
通过ρltys(i0)、~E◇(i)、~E(i)计算在线更新控制策略:
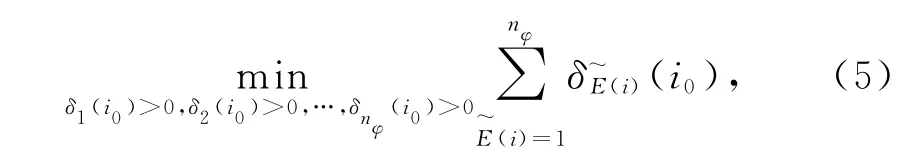
s.t.-θ(i0)≤ρltys(i0)≤θ(i0;l,t∈{1,2,…, L};y∈{1,2,…,};s∈{1,2,…,}。一步向后估计误差集合(i0)的菱形外包类(i0)中,有δk(i0)=min{(i0)},k∈{1,2,…,nφ},只能在该类中才能确保每个预测输出都能准确反映实际。
为使e(i0)∈(i0)⊆(i0)⊆,若给出δk(i0)≤1,∀k∈{1,2,…,nφ},可查询到φ(i0)∈{1,2,…,V},其为离线定义的素体样本(估计误差集合)。为估计误差集合,包含(i0),且分布在(i0)的周围;若δk(i0)>1,∀k∈{1,2,…,nφ},则~E◇(i0)未包含定义的离线最大估计误差集合,采取上一时刻的控制参数,采用(i0)顶点在i0时刻预测的一步向后估计误差,图3所示为NΩ=5,nφ=2时的估计误差集合。若离线最大估计误差集合将~E(i0)菱形集合包裹于其中,则一步向后估计误差集合参照~E(i0)近似。

图3 NΩ=5,nφ=2时的估计误差集合Fig.3 The set of estimation error when NΩ=5,nφ=2
在线估计误差状态在第P个分割包内,误差满足关系e(i0)∈(i0)⊆(i0)⊆,φ(i0)∈{1,2,…,V},也就满足状态估计x0(i0)∈X^g,^g∈{1,2,…,(2NΩ}。分割包X^g的在线扩展状态一般可被吸引域包含其中,吸引域描述为{{EN-1}(μ,φ(i0))},个数为2nφ;离线搜索到的控制器参数记为{{M(nφ,φ(i0),λ)}(μ,φ(i0))},上限数为;包含在线实时扩展状态的最优指标(最小吸引域)的控制器最优解为μ*(i0)=min{μ(μ,φ(i0))}。
在切换参数及控制器时,必须保证自动搜寻的吸引域锁定,也就是说,该优化指标单调减或保持不变,所以,在采样时均需考虑性能指标最优。如在i时刻控制器参数搜寻方式与i+a时刻保持相似的方式,必须比较性能价值指标;若μ*(i+a)<μ*(i),控制器参数自动选取i+a时刻的参数集合,否则选取i时刻的参数集合。
2 测试实验
2.1 仿真
通过动态输出反馈预测控制算法智能计算控制器及相应吸引域,再利用在线自动搜寻步骤循序渐进地在线搜索控制器参数。选取采样时间为Ts=1 s, Eδl=100,R=1,α=0.001 2,ηn=0.6+0.04(n-1), n={1,2,…,9},¯e=[0.075,1.32]T,θ(i)= diag},i0=0.99,N0=200;原点周围的正交区为ηφ=2,初始估计状态为x0(0)= [0.1,2.15]T,ε9包含所有估计误差集合,有界噪声范围选取[-0.15,0.15]。9次仿真系统误差状态轨迹如图4所示,闭环系统可收敛到(i0)=0附近。从图4可看出,实时扩展状态(i0)保持收敛稳定,实验验证了该方法的有效性。
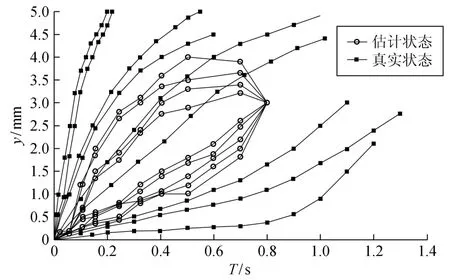
图4 误差状态轨迹Fig.4 Error state locus
对胎面缠绕系统模型进行仿真,采用多元非线性回归预测算法,系统期望输出采用1~2变化的方波,周期为100 s,跟踪步数为350,仿真结果如图5所示,其中U为控制信号输入。从图5可看出,预测输出yd能跟踪期望输出yf,但收敛速度慢,动态性能需进一步提高,且相对误差波动大,控制精度也不太高。采用动态输出反馈预测控制算法及在线更新估计误差的控制方法,仿真结果如图6所示。从图6可看出,该控制算法取得了满意的控制效果,过渡时间短,响应速度快,稳定性好,参数易调整,显示出该方法具有良好的鲁棒性和适应性。
2.2 生产试验
取200个轮胎生产成品样本做误差分析,结果如图7所示。实际缠绕的胎面外廓形状基本与设计曲线一致,仿形缠绕效果好,胎面形状误差大致分布在±2%内,轮胎质量误差大致分布在±1%内,比国际上轮胎缠绕工艺质量精度要求±2%提高了很多,生产效率也得到提升,受到用户的好评。

图5 多元非线性回归预测算法缠绕厚度预测曲线与控制信号输入曲线Fig.5 The curve of winding thickness prediction and control signal input based on the multivariate nonlinear autoregressive prediction algorithm

图6 动态输出反馈预测控制算法缠绕厚度预测曲线与控制信号输入曲线Fig.6 The curve of winding thickness prediction and control signal input based on the dynamic output feedback predictive control algorithm

图7 误差分析Fig.7 Error analysis
3 结束语
预测控制技术运用在全钢轮胎仿形缠绕的生产过程中,改善了轮胎胎面缠绕的快速与稳定特性。预测控制优化算法的改进与更新,极大地提高了国际工程轮胎缠绕行业的整体水平,仿形缠绕的精度、稳定性、抗干扰能力、生产效率均得到大幅度的提高。现阶段,这项关键技术一直被国外掌握,在控制算法的精度与快速性及数学模型优化方面,我国专家需进一步研究改进,以提升我国的轮胎生产工艺水平。
[1] 林远艳.轮胎胎面缠绕自适应预测控制研究[D].桂林:桂林电子科技大学,2006:44-85.
[2] 王存雷,臧万永.巨型工程机械子午线轮胎胎面缠绕生产线[J].轮胎工业,2010,30(5):300-302.
[3] 平续斌,丁宝苍.动态输出反馈鲁棒模型预测控制离线算法[J].自动化学报,2013,39(6):790-798.
[4] 蒋丽亚,邹媛媛,牛玉刚.多速率分段线性系统预测控制的显式设计[J].自动化学报,2013,39(5);631-636.
[5] 平续斌,丁宝苍,韩崇昭.动态输出反馈鲁棒模型预测控制[J].自动化学报,2012,38(1):31-37.
[6] 刘超刚.工业模型预测控制理论、方法及应用[D].天津:河北工业大学,2010:12-33.
[7] Hartley E N,Maciejowski J M.Reconfigurable predictive control for redundantly actuated systems with parameterized input constraints[J].Systems&Control Letters,2014,66:8-15.
[8] Ding B C,Xie L H.Dynamic output feedback robust model predictive control with guaranteed quadratic boundedness [C]//Proceedings of the 48th IEEE Conference on Decision and Control Held Jointly with the 28th Chinese Control Conference.Shanghai:IEEE,2009:8034-8039.
编辑:翁史振
Research on model predictive control for all-steel tire profiling winding process
Tao Yue,Chen Legeng
(School of Electronic Engineering and Automation,Guilin University of Electronic Technology,Guilin 541004,China)
In order to improve the stability of tire profiling winding system and control performance,according to the tire profiling winding mathematics-model,the dynamic output feedback predictive control is proposed for a system with disturbance uncertainty.The off-line error database is established by estimating the state and error set of winding model.Moreover,the estimation error is updated in real-time in the auxiliary optimization.It can calculate the real-time controller and predictive controller online.Experimental results show that the improved method is feasible and effective,and increases the controlspeed.In addition,it is suitable for real applications and the error can be controlled in a stable range.
profiling winding;predictive control;mathematics-model;dynamic output feedback
TP273.2
A
1673-808X(2015)02-0132-04
2014-03-04
国家自然科学基金(61363005);广西自然科学基金(2012GXNSFAA053221)
陈乐庚(1963-),男,广西桂林人,副教授,研究方向为工业智能控制、计算机控制及相关技术。E-mail:lg3067@163.com
陶越,陈乐庚.全钢轮胎仿形缠绕过程的模型预测控制[J].桂林电子科技大学学报,2015,35(2):132-135.
