强相依高斯序列最大值几乎处处中心极限定理
2015-06-23刘艳萍吴群英
刘艳萍,吴群英,杨 飞
(桂林理工大学理学院,广西桂林541004)
强相依高斯序列最大值几乎处处中心极限定理
刘艳萍,吴群英,杨 飞
(桂林理工大学理学院,广西桂林541004)
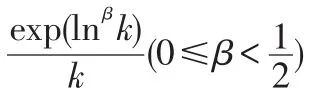
几乎处处中心极限定理;强相依高斯序列;权重
0 引言
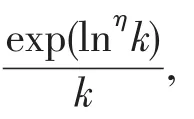
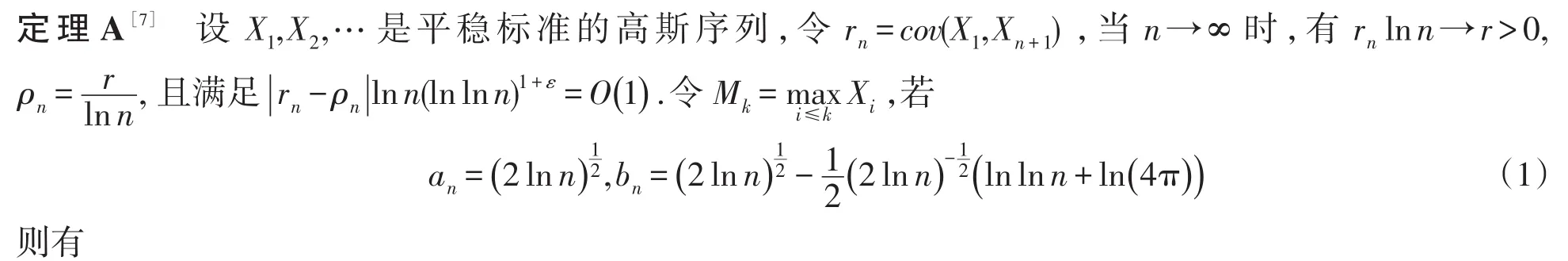
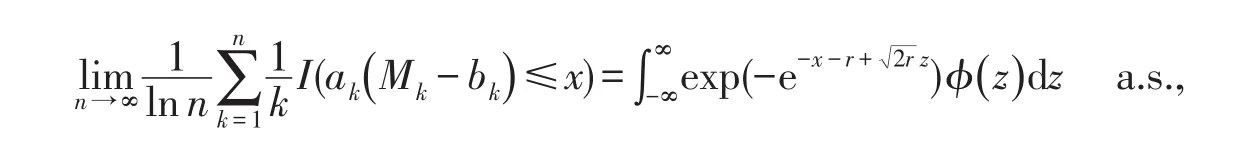
其中I(·)为示性函数, φ() x为标准正态密度函数.
1 主要结果
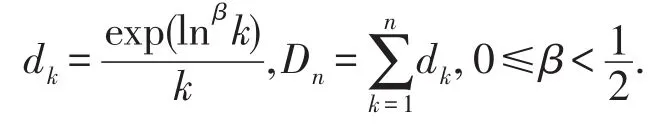
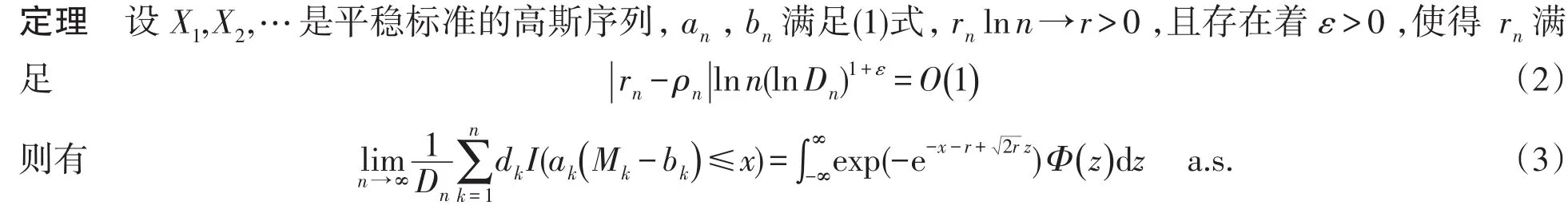
2 几个引理
为证明定理,需用到以下几个引理:
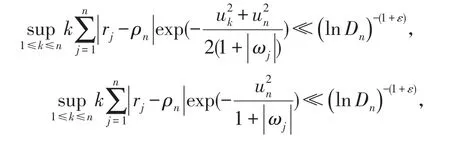
其中ε由(2)式确定.
引理1的证明类似于蔺富明[7]引理2.1的证明过程.
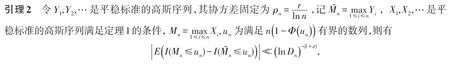
其中ε由(2)式确定.
引理2的证明运用引理1以及正态比较引理易证得.
引理3令ξ1,ξ2,…是有界随机变量,存在δ>0,使得
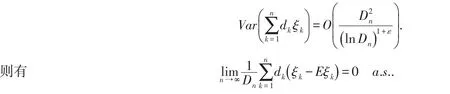
引理3的证明类似于吴群英[8]引理2的证明过程.
3 定理的证明
由注1[9],可不妨假设0<β<,因此下面仅对0<β<进行证明.当满足定理1的条件时,运用Leadbetter[10]推论6.5.2,有
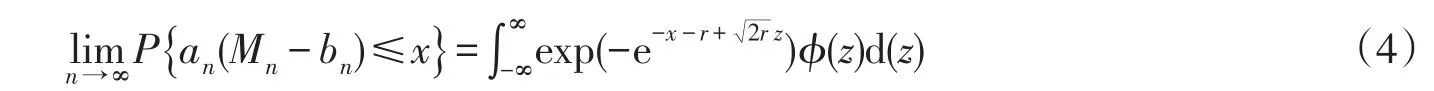
由Toeplitz引理以及(4)式可得
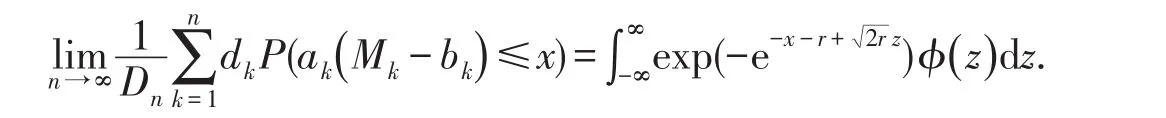
因此,要证明(3)式,只需证明
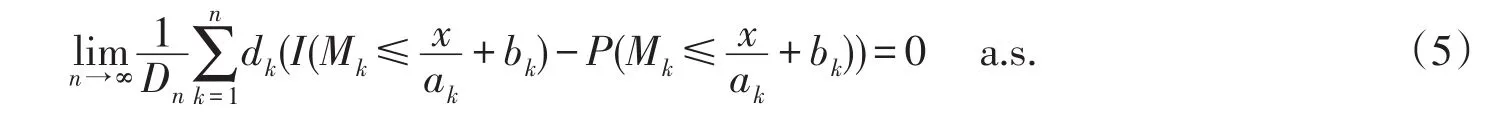
由引理3,要证明(5)式只需证明存在δ>0有

由慢变化函数的性质和ηk有界可得
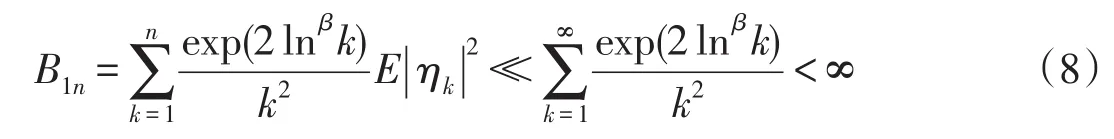
对于B,引用文献[7]中(26)式中对H的计算,有|E(ηη)|≤,由文献[9]中(11)式和(13)式对S1n的计算,取σ=min-1,1},有

[1]Brosamler G A.An almost everywhere central limit theorem[J].Math Proc Cambridge Philos Soc,1988,104(3):561-574.
[2]Schatte P.On strong versions of the central limit theorem[J].Mathematische Nachrichten,1988,137(1):249-256.
[3]Fahrner I,Stadtmüller U.On almost sure max-limit theorems[J].Statistics&Probability Letters,1998,37(3):229-236.
[4]Cheng S,Peng L,Qi Y.Almost sure convergence in extreme value theory[J].Mathematische Nachrichten,1998,19(1):43-50.
[5]Berkes I,Csáki E.A universal result in almost sure central limit theory[J].Stochastic Processes and Their Applications,2001,94(1):105-134.
[6]Csáki E,Gonchigdanzan K.Almost sure limit theorems for the maximum of stationary Gaussian sequences[J].Statistics& Probability Letters,2002,58(2):195-203.
[7]Lin F.Almost sure limit theorem for the maxima of strongly dependent Gaussian sequences[J].Electronic Communications in Probability,2009,14(1):224-231.
[8]Wu Q,Chen P.An improved result in almost sure central limit theorem for self-normalized products of partial sums[J]. Journal of Inequalities and Applications,2013,2013(1):1-12.
[9]刘艳萍,吴群英.优化权重下高斯序列最大值几乎处处中心极限定理[J].山东大学学报:理学版,2014,49(5):50-53.
[10]Leadbetter M R,Lindgren G,Rootzén H.Extremes and related properties of random sequences and processes[M].New York:Springer,1983:136-137.
(责任编辑 赵 燕)
Almost sure limit theorems for maxima of the strongly dependent Gaussian sequences
LIU Yanping,WU Qunying,YANG Fei
(College of Science,Guilin University of Technology,Guilin 541004,China)
Discussed almost sure limit theorems for maxima of strongly dependent Gaussian sequence. The almost sure limit theorem with logarithmic mean from Lin Fuming was extended to weight(0≤β<)under some mild conditions.
almost sure central limit theorem;strongly dependent sequence;weight
O211.4
A
10.3969/j.issn.1000-2375.2015.05.005
1000-2375(2015)05-0427-04
投稿日期:2015-03-21
国家自然科学基金(11361019)、广西自然科学基金重点项目(2013GXNSFDA019001)和广西硕士研究生科研教育创新计划项目(YCSZ2014158)资助
刘艳萍(1990-),女,硕士生,E-mail:xiaobudianmoon@163.com;吴群英,通信作者,教授,E-mail:wqy666@glut.edu.cn
