一类发展p(x)-Laplace方程解的存在唯一性
2015-06-23赵江艳詹华税
赵江艳,詹华税
(1.集美大学理学院,福建厦门361021;
2.厦门理工学院应用数学学院,福建厦门361024)
一类发展p(x)-Laplace方程解的存在唯一性
赵江艳1,詹华税2
(1.集美大学理学院,福建厦门361021;
2.厦门理工学院应用数学学院,福建厦门361024)
研究了具有p(x)增长条件且吸附项为 -uq(x)的一类非线性抛物型方程ut=div(|∇u|p(x)-2∇u)-uq(x),x∈Ω,0<t<T的初边值问题,其中inf p(x)>2,运用差分方法将抛物问题转化为椭圆型问题,证明了该问题解的存在性与唯一性.
初边值问题;p(x)-Laplace方程;差分法
假设Ω是具有Lipschitz连续条件的有界区域,考虑如下初边值问题
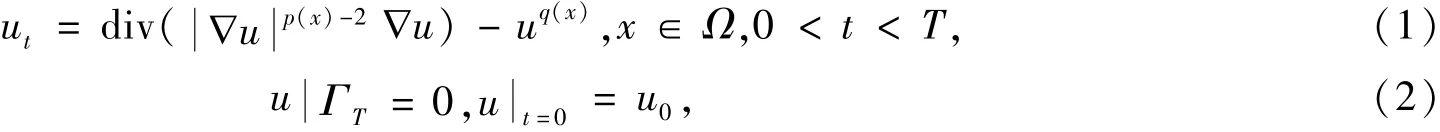
其中ΓT=∂Ω×(0,T],p(x)是可测函数.
当p(x),q(x)为常数时,很多研究者已经对这类问题做了深入的研究[1-5],并且证明了解的存在性、唯一性及其正则性等.1931年,波兰数学家W.Orlicz首先提出了变指数Lebesgue空间的概念[6].随后,O.Kovacik对变指数Lebesgue空间及Sobolev空间进行了深入的研究[7],并取得了突破性的进展.在80年代中期,V.V.Zhikov对与变指数空间有着密切相关的空间展开了研究,即具有非标准增长条件的变分空间[8].范先令在1995年前后将V.V.Zhikov的工作继续研究,并得到了很好的结果[9].p(x)增长问题可以看成是非标准增长问题的一种特殊情况,它在非线性弹性力学、流变电流学以及其他物理现象方面有着重要的应用.关于具有变指数增长条件问题的研究已经得到了很多结论[10-14].本文采用对时间差分方法研究带有吸附项的发展的p(x)-Laplace方程初边值问题在p(x)>2时解的存在性.文献 [10]中吸附项为f(x,t,u),本文采用类似的思想,将其吸附项给定为 -uq(x),由于涉及到不同的计算技巧,文中对其进行了具体的不同于文献 [10]的处理.
1 主要结论
定义1称函数u(x,t)是式 (1)~(2)的弱解,如果u满足以下条件:
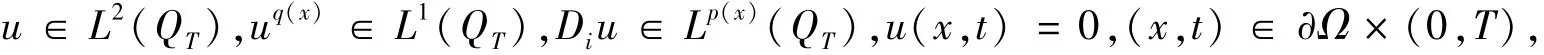
在迹的意义下,并且对于任意的φ∈C∞0(QT),以下积分等式成立:
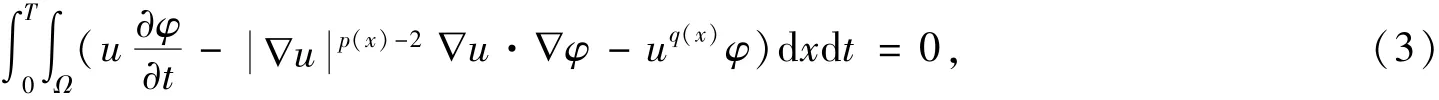
对任意的ψ(x)∈C∞0(Ω),有成立,其中QT=Ω×(0,T).
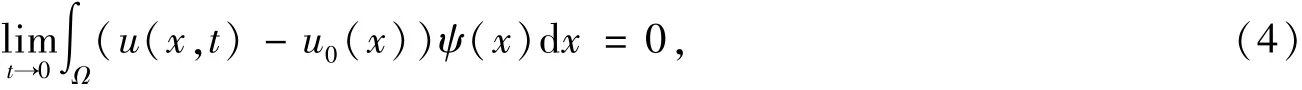
为了研究式 (1)~(2)解的整体存在性,需要对q(x)做出限制,即0≤q(x)<p--1.下面给出本文的主要结果.
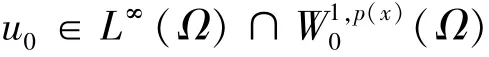
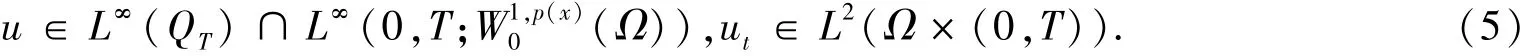
定理2满足定理1的非负解是唯一的.
2 一类差分方程的弱解存在性
首先,令
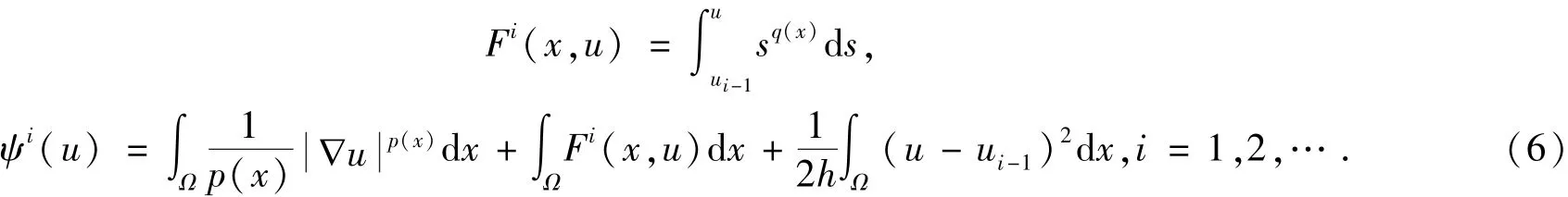
定义
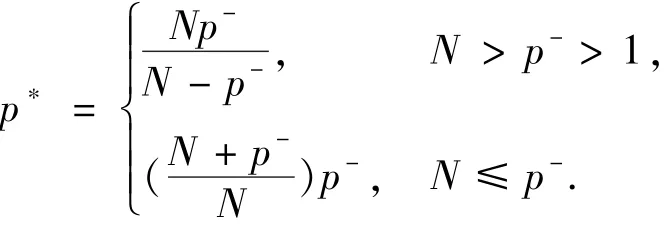
类似文献可证明引理1.
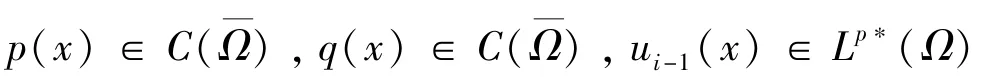
引理2令u+=max{0,u}假设u是引理1所得最小值,则对任意k≥1,u和-u满足
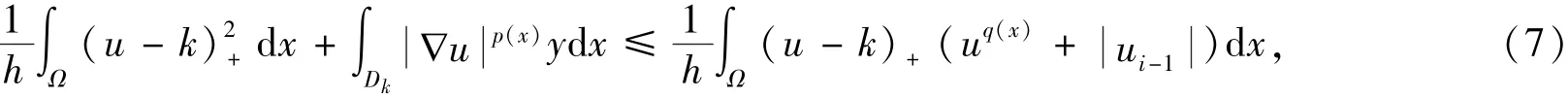
其中Dk={x∈Ω:u(x)>k}.
证明对于任意0≤ε<1,有u-ε(u-k)+∈S,以及
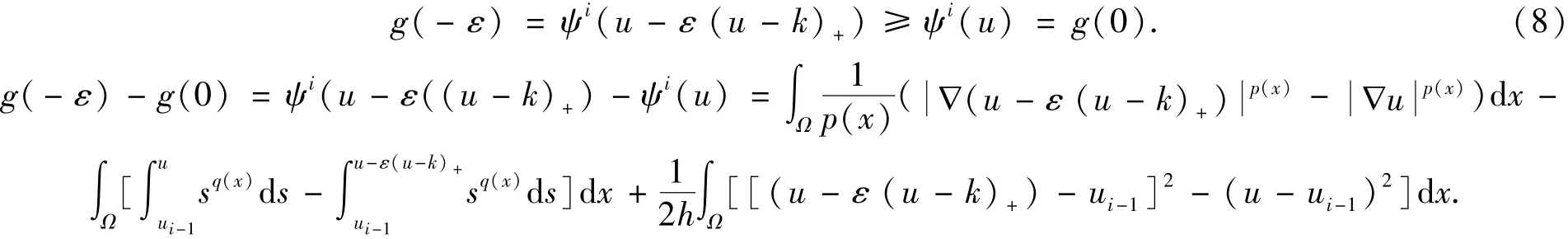
记
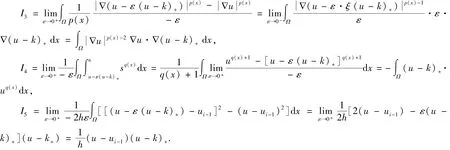
现在考虑以下问题:
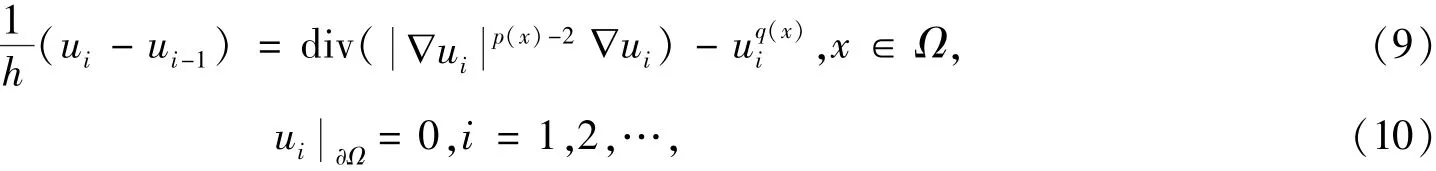
其中h为大于零的常数.
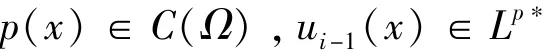
证明根据引理1,类似于引理2,对于0<ε<1和η∈C∞0,有ui±εη∈S,并且有
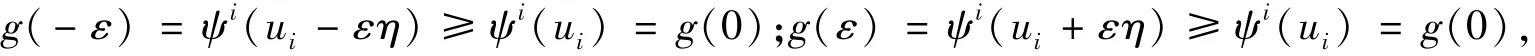
因此可得
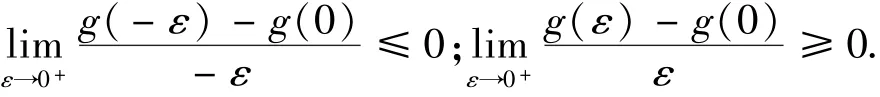
将ψi(u)的定义代入即可得:
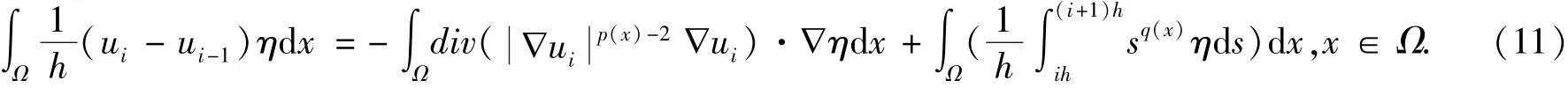
即证ui是式 (9)~(10)的一个弱解.
3 弱解的整体存在性和唯一性
假设lh≤T<(l+1)h,其中l为整数.定义u(h):Ω×[0,∞)→R使得
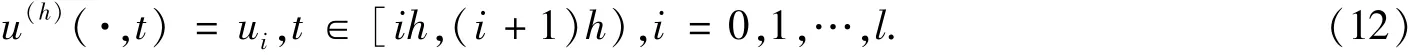
其中ui是引理3中得到的弱解.
下面将证明序列u(h)收敛,并且证明极限函数u即是问题 (1)~(2)的解.
令
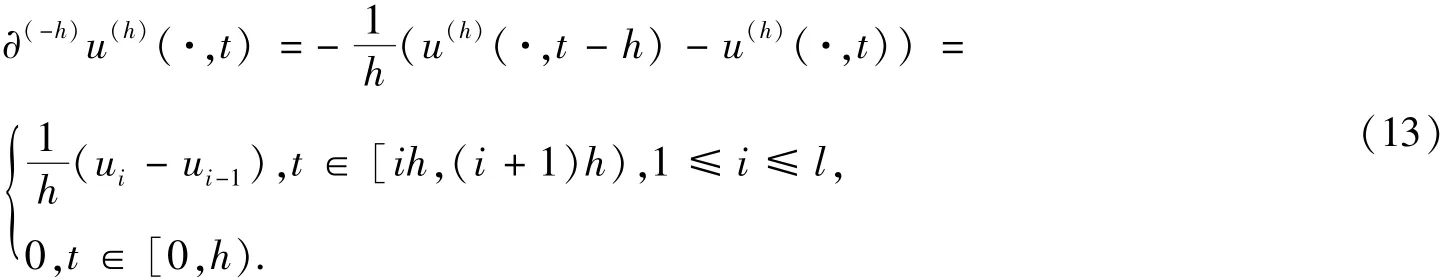
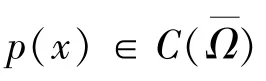
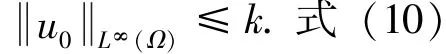
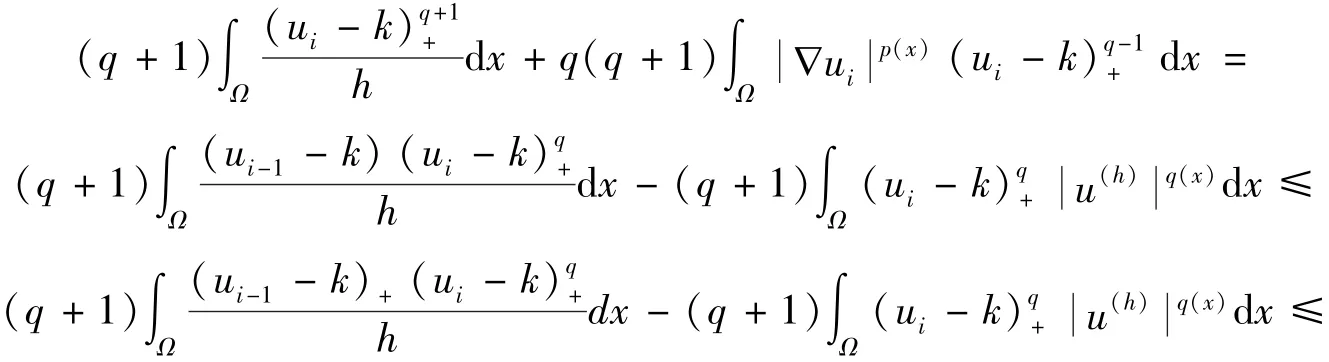
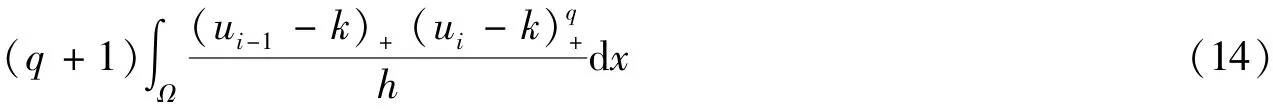
因此,

在上式中对i进行求和,结合u(h)的定义,可以得到
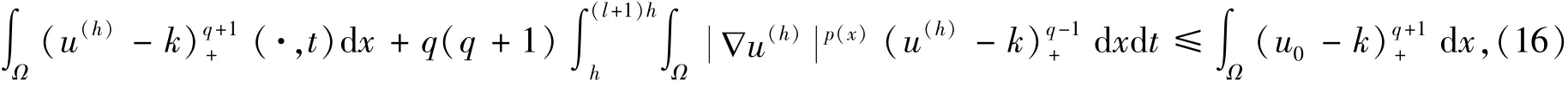
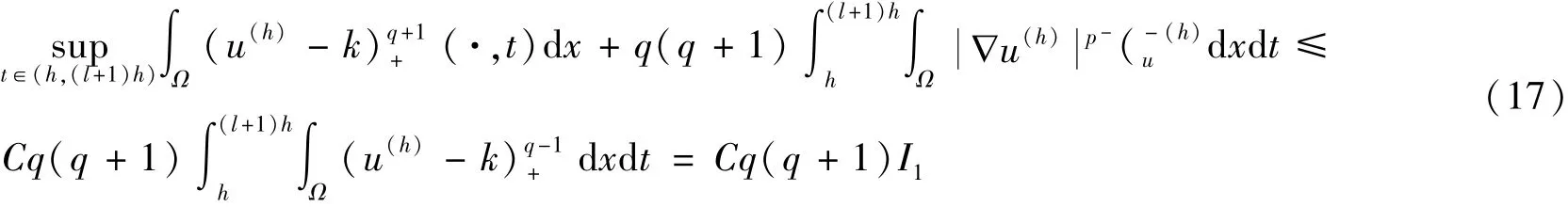
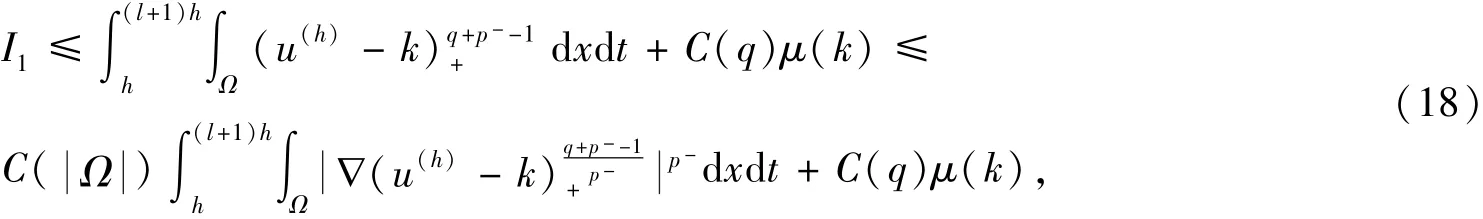
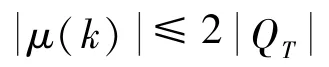
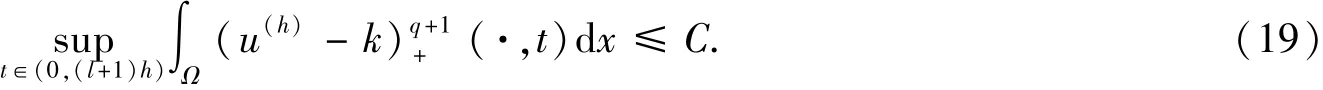
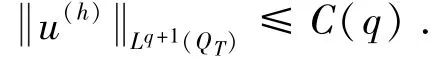
注释1根据引理4的证明过程,在其过程中取k=0和q=1,则有

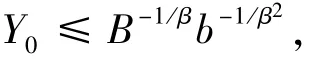

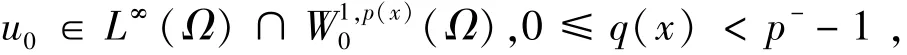
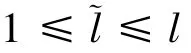
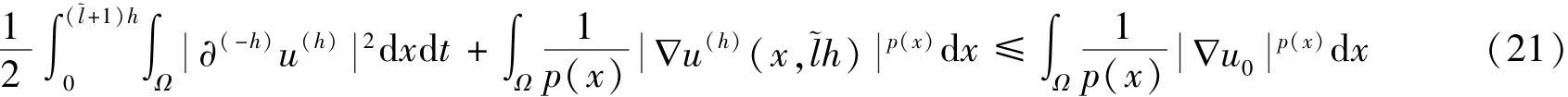
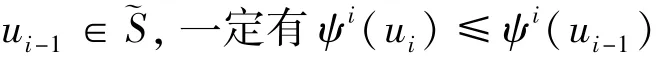
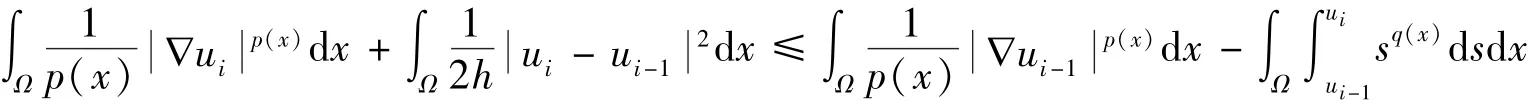
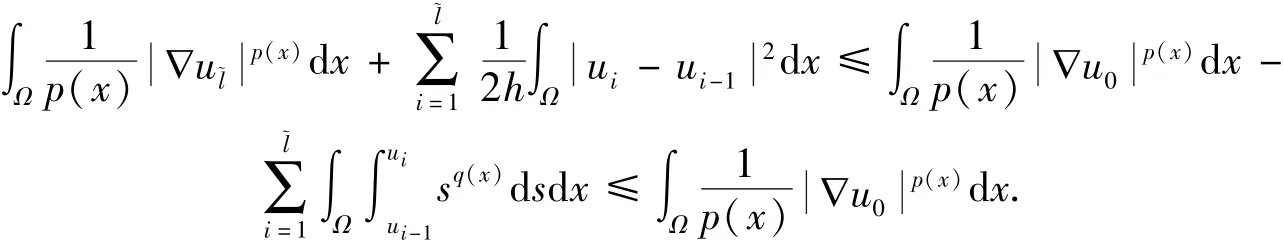
定义一个新的泛函w(h),
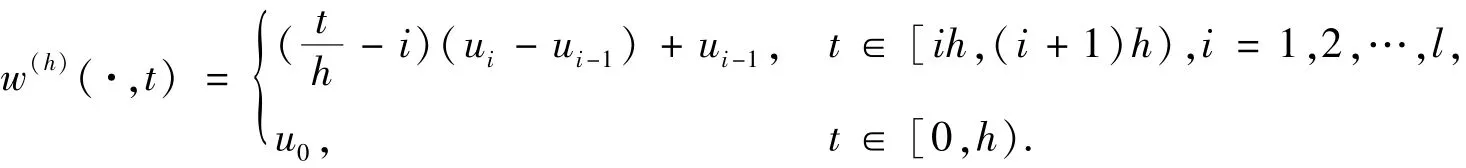
则可以得到:
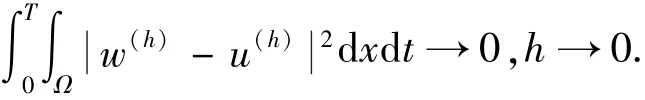
证明直接计算可得
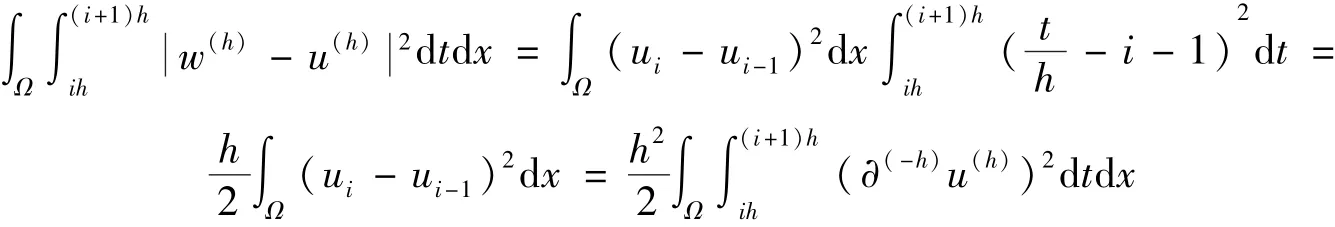
引理8根据注释2,可得存在一个新定义的子序列{u(h)}使得:当h→0时

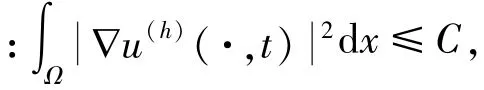

从而可得,

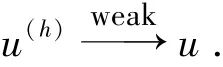
即证存在一个子列u(h)使得 (23)成立.接下来考虑w(h).因为
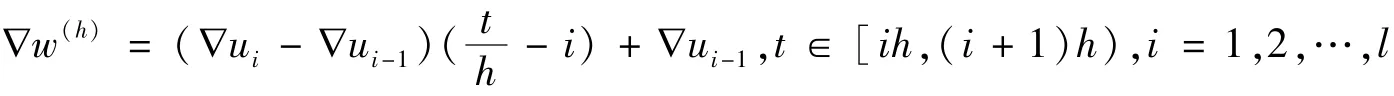
根据式 (26)(27)和引理7,可以得到w(h)和∇w(h)在L2(QT)中一致有界.因为
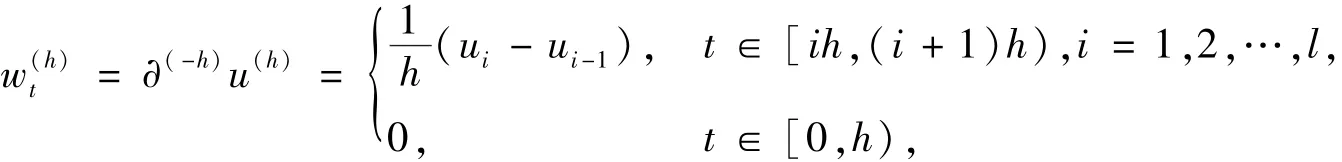
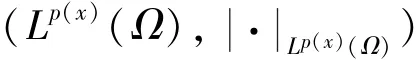


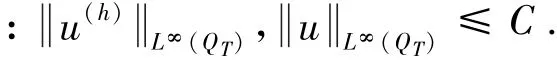
根据Hölder不等式,当h→0时
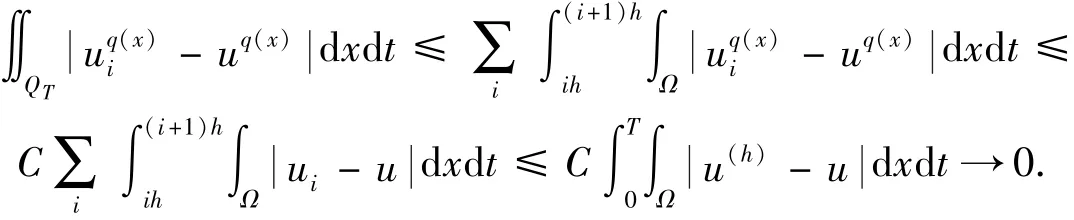
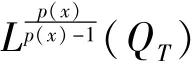
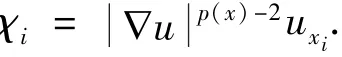
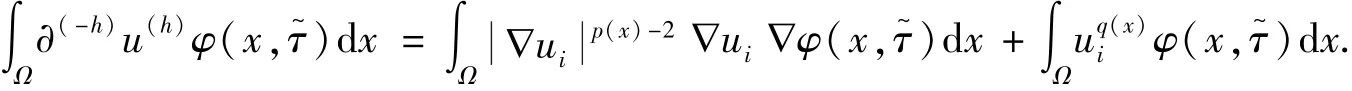
对τ~进行积分,结合引理7,8和注释1可以证得u是方程(1)的一个弱解.同时,类似于[10]可以证明u满足初始条件.
证明定理2下面证明式(1)~(2)解的唯一性,证明方法类似于文献 [10].
假设u,v是式 (1)~(2)的两个非负解,取u-v作为试验函数,可以得到:
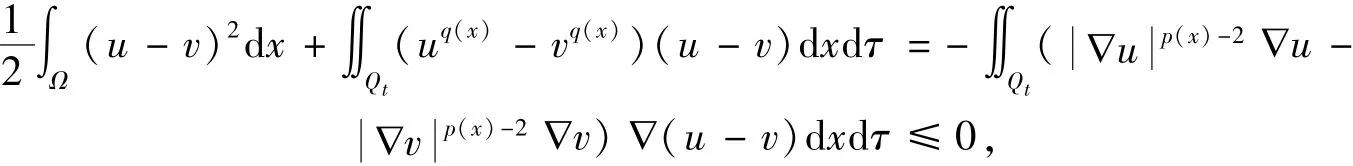
由中值定理可得,
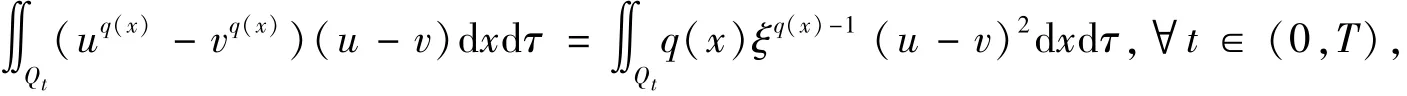
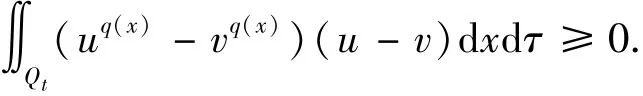
由此可得u=v,即唯一性得证.
[1]DIBENEDETTO E.Degenerate parabolic equations[M].New York:Springer-Vela,1993.
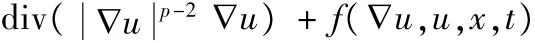
[3]ZHAO J N.On the cauchy problem and initial traces for the evolution p-laplacian equations with strongly nonlinear sources[J].J Diff Eqs,1995,121:329-383.
[4]ZHAN H SH.The nonexistence of the solution for quasilinear parabolic equation related to the p-Laplacian[J].WSEAS Tran on Math,2012,11(8):695-704.
[5]ZHAN H SH.Solution to nonlinear parabolic equations related to the p-Laplacian[J].Chinese Ann Math Ser B,2012,33(4):767-782.
[6]ORLICZ W.Überkonjugierte exponentenfolgen[J].Studia Math,1931,3:200-212.
[7]KOVACIK O,RAKOSNIK J.On spaces Lp(x)(Ω)and Wm,p(x)[J].Czech Math J,1991,41:592-618.
[8]ZHIKOV V V.Averaging of functionals of the calculus of variations and easticity theory[J].Izv Akad Nauk SSSR Ser Mat,1986,50:675-710.
[9]FAN X L,ZHAO D.Regularity of minimizers of variational integrals with continuous p(x)-growth conditions[J]. Chinese J Contemp Math,1996,17:327-336.
[10]LIAN S Z,GAO W J,YUAN H J,et al.Existence of solutions to an initial Dirichlet problem of evolutional p(x)-Laplace equations[J].Ann I H Poincare-AN,2012,29:377-399.
[11]VÄTH M.Global bifurcation of the p-Laplacian and related operators[J].J Differential Equations,2005,213:389-409.
[12]PENG L Q.Non-uniqueness for the p-harmonic heat flow with potential into homogeneous spaces[J].Chinese Ann Math Ser A,2006,27:442-448.
[13]FAN X L,ZHAO D.On the spaces Lp(x)(Ω)and Wm,p(x)[J].J Math Anal Appl,2001,263:424-446.
[14]BERGER M S.Nonlinearity and functional analysis:Lectures on nonlinear problems in mathematical analysis[M]. New York-London:Pure and Applied Mathematics,Academic Press,1977.
Existence and Uniqueness of Solutions to the Evolutionary p(x)-Laplacian Equation
ZHAO Jiang-yan1,ZHAN Hua-shui2
(1.School of Sciences,Jimei University,Xiamen 361021,China;2.School of Applied Mathematics,Xiamen University of Technology,Xiamen 361024,China)
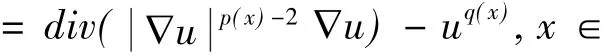
initial-boundary value problem;p(x)-Laplacian equation;difference method
O175.26
A
1673-4432(2015)05-0094-07
(责任编辑 李 宁)
2015-04-01
2015-09-30
赵江艳 (1987-),女,硕士研究生,研究方向为偏微分方程.通讯作者:詹华税 (1966-),男,教授,博士,研究方向为数学物理方程、微分几何与系统工程.E-mail:2012111007@xmut.edu.cn
