光纤陀螺组合的多尺度多传感器数据融合

刘 颖, 蔡秀梅, 刘 瑾

(西安邮电大学 自动化学院， 陕西 西安 710121)

光纤陀螺组合的多尺度多传感器数据融合

刘 颖, 蔡秀梅, 刘 瑾

(西安邮电大学 自动化学院， 陕西 西安 710121)

针对四个光纤陀螺的冗余组合，提出一种多尺度多传感器数据融合算法。该算法对4个光纤陀螺的冗余组合数据进行预处理，并对各个尺度上小波变换的系数采用自适应权值的方法进行数据融合，最后采用合适阈值和阈值函数对融合后的小波系数进行重构。仿真结果表明，该算法可以有效提高光纤陀螺组合系统的可靠性和精度,融合后的光纤陀螺组合精度可以提高一个数量级。

光纤陀螺；冗余设计；小波去噪；数据融合

近年来，随着惯性导航系统的应用领域不断延伸，对光纤陀螺性能的要求也不断提高。光纤陀螺具有成本低、体积小等优点[1]，而惯性导航系统的可靠性和精度主要取决于其核心器件陀螺组合[2-3]。针对目前光纤陀螺精度和可靠性不够高的问题，采用冗余技术设计光纤陀螺组合，可快速满足惯性导航的需求。文献[4]将冗余技术引入捷联惯导系统，使捷联惯导系统可靠性迅速提高；文献[5]提出了四冗余惯导系统的配置方案，并对配置方案的可靠性、精度、故障检测及隔离等内容进行了分析论证；文献[6]研究了捷联惯导陀螺仪冗余配置的原则和结构方案对比、选择及相应的可靠性评估与系统优化。这些文献都只是分析了冗余配置方案及其可靠性，并没有对冗余数据进行处理，精度未能提高。

目前多传感器数据融合算法在传感器数据处理中的应用越来越广泛[7]。文献[8]采用了Kalman滤波和小波变换相结合，对三个微机电陀螺仪的数据进行了融合，融合后的精度得到了很大的提高。文献[9]通过研究小波变换各尺度上的平滑信号和细节信号的统计特性，分析了小波域多尺度数据融合算法的优越性。

本文拟采用基于小波变换的多尺度多传感器数据融合的数据处理算法，对4个光纤陀螺的冗余组合数据进行预处理，使每个方向上各有4组数据，根据数据的测量精度建立权值分配曲线，确定加权因子，然后对每个方向上的各组数据进行小波分解，对在每个尺度上的数据进行融合，最后采用阈值和阈值函数有选择的保留小波系数进行重构。

1 数据预处理

光纤陀螺组合的冗余结构实体模型如图1所示。该结构将1、2、3号陀螺分别在东、北、天方向上安装，第4号陀螺在设计时要保证其敏感轴与1、2、3号陀螺的敏感轴的夹角均为54.735°。

图1 实体模型

4个光纤陀螺系统的冗余设计的可靠性是原来传统三只光纤陀螺系统可靠性的1.5倍[5-6]。在进行数据融合之前要先进行数据预处理。

一般来说，4个光纤陀螺的测试数据均具有随机误差的特性[10]。设4个陀螺的测试数据分别为

X1={x11,x12,…，x1m},

X2={x21,x22,…，x2m},

X3={x31,x32,…，x3m},

X4={x41,x42,…，x4m},

其中

m=3k (k=1,2,…,n),

xim为第i个陀螺的第m个测试数据。

由于X4为X1,X2和X3的矢量和，通过矢量的加减运算可以将数据分为

X4,1={x41,x44,…,x4m-2},

X4,2={x42,x45,…,x4m-1},X4,3={x43,x46,…,x4m}。

利用X2和X3将X4,1的数据投影到东向上，通过X1和X3将X4,2投影到北向上，通过X1和X2将X4,3投影到天向上。通过X4的数据结算可以看出，1、2、3、4号陀螺无论哪一个出现故障，系统均能正常工作。

同理，将X1测试数据分为

X1,1={x11,x14,…,x1m-2},X1,2={x12,x15,…,x1m-1},X1,3={x13,x16,…,x1m}。

依此类推，将X2的测试数据分为

X2,1={x21,x24,…,x2m-2},X2,2={x22,x25,…,x2m-1},X2,3={x23,x26,…,x2m},

将X3的测试数据分为

X3,1={x31,x34,…,x3m-2},X3,2={x32,x35,…,x3m-1},X3,3={x33,x36,…,x3m}。

X1,1,X1,2和X1,3是等精度的，同理，X2,1,X2,2和X2,3是等精度的，X3,1,X3,2和X3,3是等精度的。

通过这样的数据处理，X1,1,X1,2,X1,3和X4,1为东向4个角速率传感器的测量值，X2,1,X2,2,X2,3和X4,2假想为北向4个角速率传感器的测量值，X3,1,X3,2,X3,3和X4,3假想为天向4个角速率传感器。

数据预处理过程出现了大量的冗余数据，在东、北、天方向上相当于4个独立的传感器共同测试，为多传感器数据融合提供了条件。但是这样的数据处理在某种程度上会将降低系统的响应速度，对于响应速度要求较高的应用，可以通过插值运算来满足要求。

2 自适应权值的确定方法

在每个方向上的四组数据中，有一组的精度和其他三组的精度不同，在数据融合时的权值可以采用自适应权值的方法来确定。

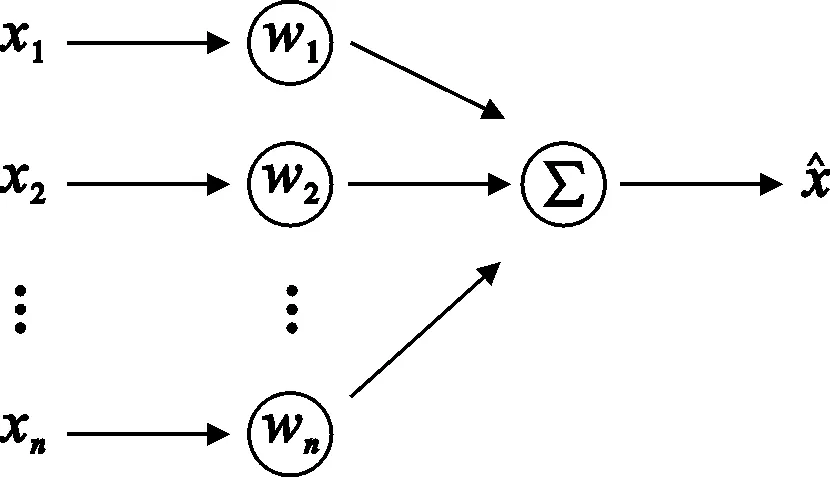
图2 自适应加权数据融合算法

根据自适应加权数据融合模型，可知

(1)

总的均方差为

(2)

由于测量值x1,x2,…,xn相互独立，且是真值x的无偏估计，则

(3)

由式(3)可知，总的均方差δ2是各个权的多元二次函数，因此必然存在最小值。由多元函数求极值理论可知,当

时，总均方差δ2存在最小值

(4)

为了节约计算时间，简化计算过程，可以取不等精度的两组数据，计算出两组数据的自适应权值的比值，然后通过

可以确定四组数据分别对应的权值。

3 基于小波变化的多传感器融合算法

以数据预处理后东向的四组数据为例，来说明基于小波变换的多尺度融合算法的基本步骤。

步骤1 将四组数据分别进行小波分解。

采用Mallat提出的快速分解算法，可以有效减小计算量，其分解算法[11]为

(5)

其中H，G相当于信号处理中的低通滤波器和带通滤波器[12];CJ为尺度系数，DJ为小波系数,下标J和J-1表示随着分解递推。

步骤2 采用自适应权值的方法确定四组数据数据融合的权值。

步骤3 将四组数据分别在各分解尺度上进行自适应加权数据融合，对融合后的小波系数进行阈值去噪处理。

步骤4 确定小波各尺度的阈值。

小波阈值λ在不同的尺度取同一值，不能够很好反映噪声在小波变换各尺度上的传播特性，去噪效果差，因此采用一种随尺度改变的阈值确定方法

(6)

其中

步骤5 按阈值函数估计每尺度的小波系数

(7)式中α∈[0,1]，为阈值函数的调节因子；ωj,k为小波系数。阈值函数由一个多项式决定，与传统阈值函数不同，能最大程度保留真实信号，消减接近或低于阈值的小波系数，使之远远小于其他小波系数[3]。

步骤6 将估计后的小波系数进行重构，得到的信号，就是融合后的结果。

CJ=H*CJ-1+G*DJ-1,

(8)

其中H*,G*分别为H，G的共轭转置矩阵。

4 试验验证

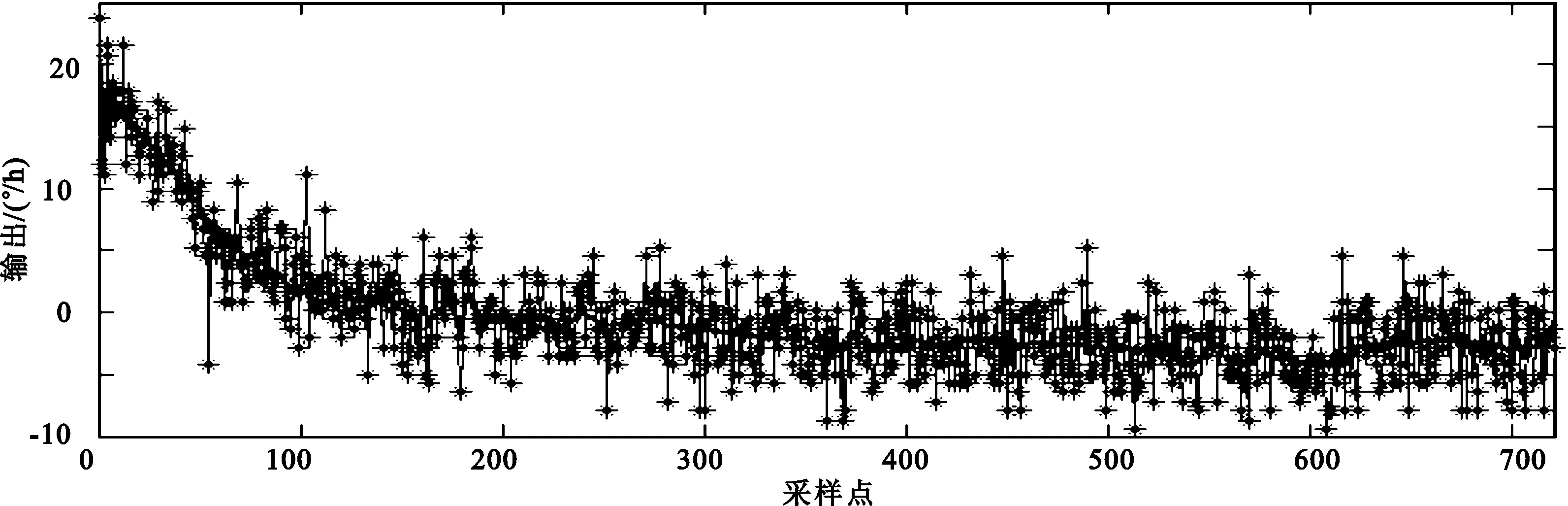
对4个光纤陀螺进行数据融合实验，为了便于观察，取陀螺的10 s累加值，每只陀螺测试时间为2小时，测试完后，去掉4个陀螺的角速度信息。采用基于小波变换的阈值去噪算法进行处理，4个光纤陀螺的数据处理前的原信号和去噪后的数据如图3所示，点为原信号，较平滑的线为去噪后的数据。

图4为基于小波变换的多尺度多传感器融合后的数据。图3和图4均采用db4小波基，小波分解尺度J=4，调节因子α=0.5进行仿真。

(b) 北向陀螺静态测试数据

(c) 天向陀螺静态测试数据

(d) 倾斜方向陀螺静态测试数据

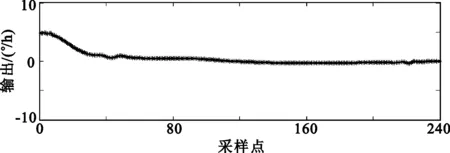
(a) 东向融合后的数据

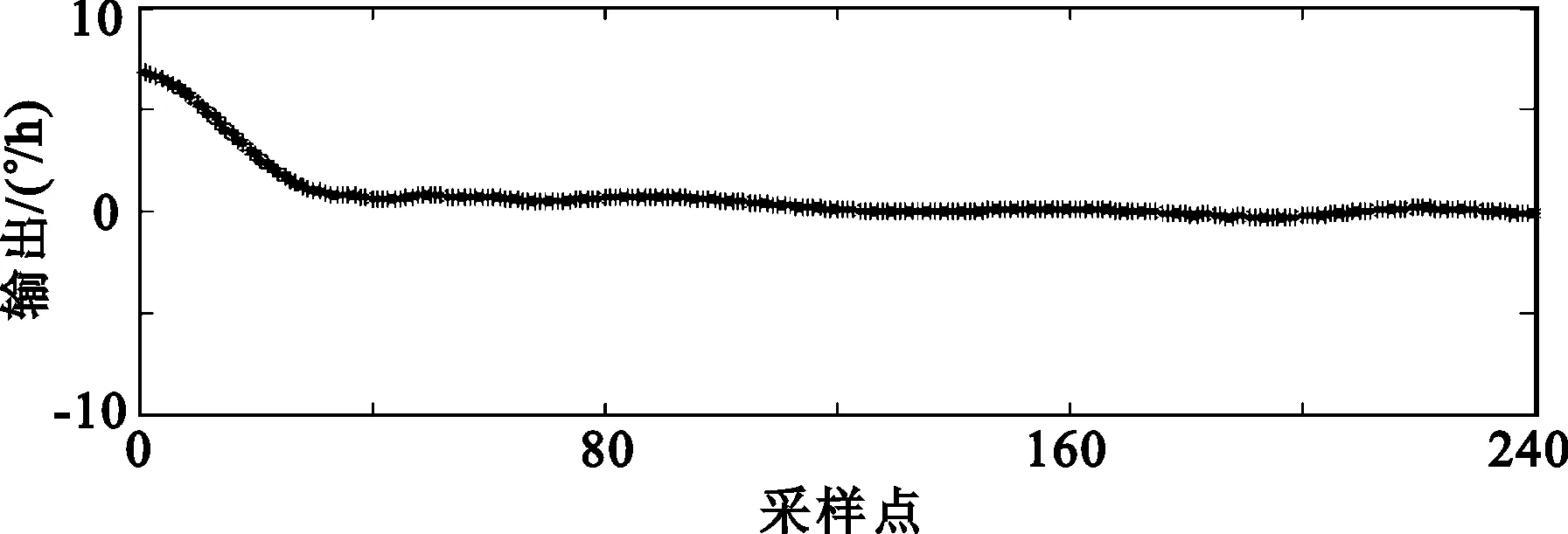
(b)北向融合后的数据

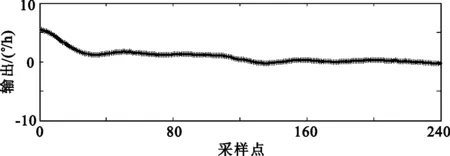
(c) 天向融合后的数据

从图3、图4分别可以看出，基于小波变化的阈值去噪算法后，可以在很大的程度上减小光纤陀螺的噪声；而基于小波变换的多尺度多传感器数据融合算法效果比基于小波变化的阈值去噪算法更好。

根据光纤陀螺的测试标准，计算数据处理前后数据的零偏稳定性，如表1所示，经数据融合后三个方向上的测试精度均提高了一个数量级。

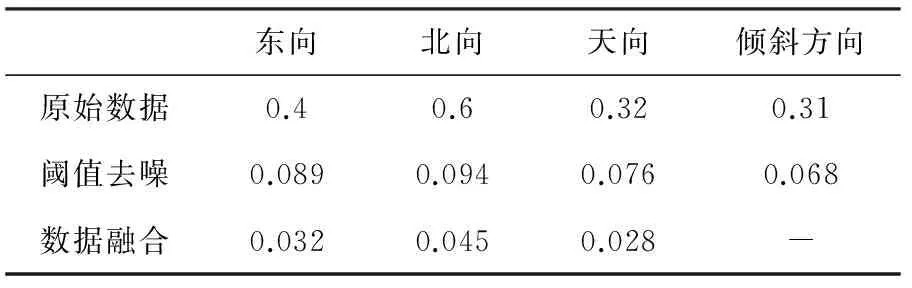
表1 三个方向输出数据的零偏稳定性

5 结束语

针对4个光纤陀螺的冗余结构，提出了一种多尺度多传感器数据融合算法。通过数据预处理实现了东、北和天方向上的多角速率传感器输出，基于小波变换将四组数据分别在各分解尺度上进行自适应加权数据融合，采用阈值和阈值函数有选择的保留小波系数进行重构。仿真结果表明该算法可使零偏稳定性提高一个数量级，达到设计要求。

[1] 刘颖,李言,徐金涛.光纤陀螺自适应阈值滤波新方法[J].应用科学学报,2010,28(1):56-60.

[2] Lefevre H. The Fiber Optic Gyroscopes[M]. Norwood: Artech House, 1993: 34-40.

[3] 朱奎宝,张春熹,宋凝芳.光纤陀螺角度随机游走对惯导系统影响[J].压电与声光,2007,29(3):292-296.

[4] 夏克寒,许化龙.冗余技术在捷联惯导系统中的应用[J].上海航天,2002(3):25-28.

[5] 王民钢,攀英平,催伟成,等.四冗余陀螺系统配置研究[J].弹箭与制导学报,2006,26(3):40-44.

[6] 潘鸿飞,袁立群,任尚云.捷联惯导陀螺仪冗余配置研究[J].上海航天,2003(1):35-38.

[7] 聂文梅，卢光跃.无线传感器网络中丢包扩散卡尔曼算法的改进[J].西安邮电大学学报,2013,18(4):35-38.

[8] 柯熙政,任亚飞.多尺度多传感器融合算法在微机电陀螺数据处理中的应用[J].兵工学报,2009,30(7):995-998.

[9] 任亚飞,柯熙政.多尺度小波分解融合在微机电陀螺数据处理中的应用[J].应用科学学报,2010,28(4):394-398.

[10] 李家垒,许化龙,何婧.光纤陀螺信号的小波包区噪及改进[J].光学学报,2010,30(8):2224-2228.

[11] 潘泉,张磊,孟晋丽,等.小波滤波方法及应用[M].北京:清华大学出版社,2005:64-65.

[12] Mallat S. Singularity detection and processing with wavelets [J]. IEEE Transactions on Information Theory, 1992, 38(2): 617-643.

[责任编辑:祝剑]

Multi-scale multi-sensor data fusion of fiber optic gyroscope combination

LIU Ying, CAI Xiumei, LIU Jin

(School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A multi-scale and multi-sensor data fusion algorithm is designed for redundant fiber optic gyroscope combination. Four groups of virtual sensor data are produced in three directions of east, north and top, based on the four fiber optic gyroscopes data preprocessing. There are four sets of data in each direction. A wavelet transform are done on data from each group. Data fusion using adaptive weights is carried out in the wavelet coefficients in every scale. Wavelet coefficients are reconstructed by using the right threshold and threshold function after the data fusion. Experimental results show that this scheme can effectively improve the precision and reliability of fiber optic gyroscope combined system. The precision of the three directions can be improved by one order in magnitude.

fiber optical gyroscope, redundancy design, wavelet de-noise, data fusion

2014-04-10

陕西省教育厅科学研究计划资助项目(2013JK0993，2013JK0197)；西安邮电大学青年教师科研基金资助项目(ZL2013-30)

刘颖(1979-)，女，博士，讲师，从事光纤传感和数据处理研究。E-mail: ly676@163.com 蔡秀梅(1975-)，女，博士，副教授，从事数字图像处理研究。E-mail: caixiumei@xupt.edu.cn

10.13682/j.issn.2095-6533.2015.01.015

TP391.9

A

2095-6533(2015)01-0075-05