木星-火星-航天器系统的零速度曲面和转移轨道的数值研究

唐桂琴，高发宝，王 坤，邱林飞

(扬州大学 数学科学学院，江苏 扬州 225002)

木星-火星-航天器系统的零速度曲面和转移轨道的数值研究

唐桂琴，高发宝，王 坤，邱林飞

(扬州大学 数学科学学院，江苏 扬州 225002)

针对木星-火星-航天器系统，根据欧拉-拉格朗日方程建立了航天器的动力学方程，并通过数值模拟，研究了系统的零速度曲面和Jacobi常数的几何结构的关系，设计了一条可用于多任务轨道的从火星至木星的转移轨道。

木星；火星；零速度曲面；转移轨道；数值模拟

0 引言

在深空探测任务中，假设其中一个质量体的质量与其他两个天体的质量相比时，小到可以忽略，这样的三体问题就称为限制性三体问题。这个小质量的天体一般称为无限小质量体，把两个大质量的天体称为有限质量体。由于无限小质量体的质量可以看成无限小，所以就可以不考虑它对另外两个有限质量体的吸引，也就是说，它不影响这两个有限质量体的运动。如果三体中的这两个有限质量体以一定的角速度绕其公共质心作匀速圆周运动，则此三体问题就称为圆型限制性三体问题[1-5]。随着第二轮深空探测热潮的到来，火星、木星等天体正逐渐成为各航天大国的探测重点[6-7]。自1976年火星着陆器第一次成功登陆火星以来，人类已经发射多个火星探测器，对火星的探测积累了丰富的经验。由于地球距离木星要比火星远得多，因此人类对木星的探测也少得多。但如果借助探索火星的成功经验，设计一条火星至木星的转移轨道，就可以在探测火星的同时探测木星。当然，由于限制性三体问题存在相应的零速度曲面，使得无限小质量体不能无限制地在宇宙空间中任意飞行。在实际探测任务中，零速度曲面具有极其重要的应用价值，利用零速度曲面不但可以确定火箭飞向月球的最小速度，在讨论运动区域时也具有重要的意义，近年来还被用来研究双星的演化。

本文将深入分析由火星-木星-航天器组成的限制性三体系统的零速度曲面的几何结构，讨论多种情形下Jacobi常数对航天器飞行区域的影响，同时针对其中最重要的一种情形，数值模拟出一条航天器可在火星和木星之间飞行的转移轨道。该轨道可用于多任务轨道的设计，相比独立探测火星和木星来说，将会减少大量的能源消耗并节省可观的费用。

1 圆型限制性三体模型

首先介绍两个常用坐标系：质心惯性坐标系OXYZ和质心转动坐标系oxyz。质心惯性坐标系OXYZ中由航天器M，木星M1和火星M2组成的系统，坐标系的原点O在M1和M2的质心(如图1所示)，其中X-Y平面是木星-火星系统的轨道平面，M1和M2围绕它们的公共质心作圆周运动，航天器M只受到M1和M2的引力作用。X轴由M1指向M2，Y轴与之垂直并满足右手坐标系(默认Z轴垂直于轨道平面X-Y)，M，M1和M2的质量分别为m，m1和m2，且m≪m1，m2。

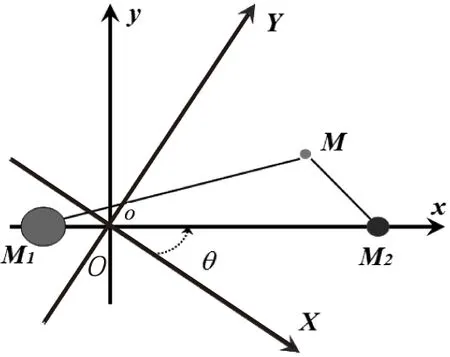
图1 惯性和转动坐标系

方便起见，假设[m]，[L]和[T]分别为质量单位、长度单位和时间单位，LM1M2为火星和木星的平均距离，ω为火星和木星相对运动的角速度，通常按照[m]=m1+m2，[L]=LM1M2，[T]=[LM1M2/(G(m1+m2))]1/2=1/ω对系统进行无量纲化。图1中θ为M1和M2的连线绕其质心转过的角度，系统的质量比率μ=m2/(m1+m2)，火星和木星到其公共质心的无量纲距离分别为1-μ和μ。质心转动坐标系oxyz的原点o和质心惯性坐标系的原点O重合，其坐标轴x和y以单位角速度围绕其质心作逆时针转动(相对于惯性坐标系中的X轴和Y轴)，并假设两个坐标系在时间t=0时重合，则有θ=t。如果(x，y，z)表示小天体M在质心转动坐标系中的位置，则有

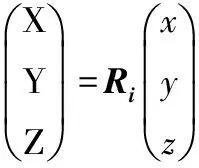
(1)

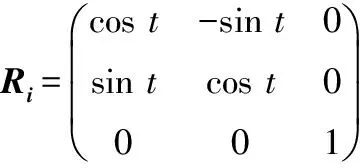
将方程(1)两边对时间t求导，得到

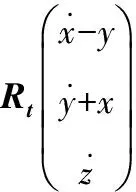
(2)

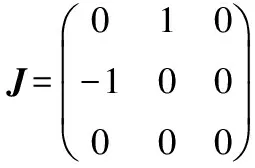
于是在质心转动坐标系下，系统的拉格朗日函数为：

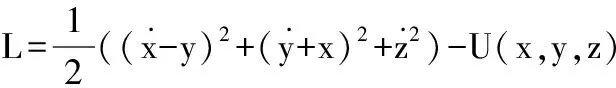
(3)

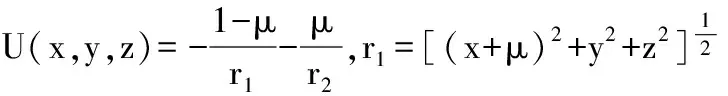
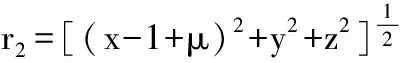
将方程(3)代入欧拉-拉格朗日方程[3]，得到质心转动坐标系oxyz下航天器运动方程：

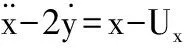
(4a)

(4b)

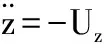
(4c)

定义广义势能Ω(x，y，z)为：

(5)

则质心转动坐标系oxyz中航天器运动的无量纲方程可改写为：

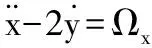
(6a)

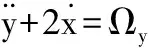
(6b)

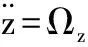
(6c)

2 木星-火星-航天器系统的零速度曲面分析

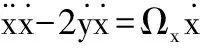
(7a)

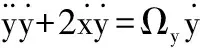
(7b)

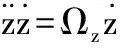
(7c)

将方程(7a)-(7c)3式的两边分别相加，得

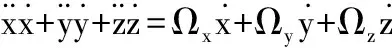
(8)

对方程(8)两边积分得到航天器的运动状态流形：

2Ω(x，y，z)-v2=C，

(9)

由于航天器的飞行区域由v2≥0决定，因此航天器的运动区域将由此流形决定。方程(7)在三维空间中所张成的曲面称为零速度曲面或Hill曲面，在二维平面上则表现为一系列的曲线，称为零速度曲线。二者的几何结构将随着Jacobi常数C的变化而变化。根据美国国家航空航天局的官方数据，m1=1898.3e+24 kg，m2=0.64174e+24 kg，那么系统的质量比率μ=3.379 461 236e-04。

三维空间中，航天器的禁飞区域或零速度面(2.999 67≤C≤3.023)如图2所示。当Jacobi常数C的取值逐渐减小时，表明系统消耗的能量逐渐增大，那么零速度曲面所张成的范围越来越小，此时航天器的飞行区域逐渐开阔；当Jacobi常数C的取值逐渐增大时，此时系统消耗的能量逐渐减小，航天器没有足够的能量，就像陷入了一个势阱区域，其飞行的区域也就越来越小，最终甚至飞不出图中间木星所在的“大圆”区域或者火星所在的“小圆”区域。

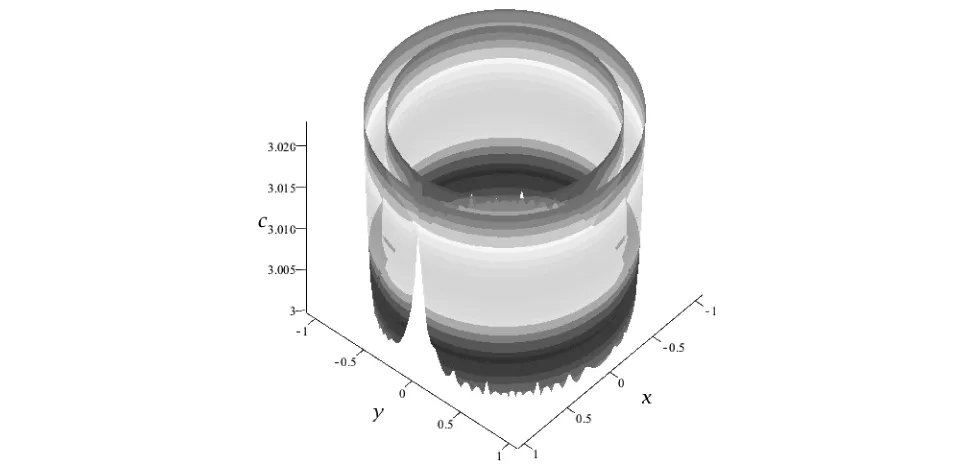
图2 航天器的零速度曲面C∈[2.999 67，3.023]

二维平面中，当C=3.023时，图2中最上面的区域由三个“圆”组成，其中最外围的“大圆”围绕着中间的木星所在区域的“大圆”以及火星所在区域的“小圆”，且三者呈相离状态，说明此时航天器仅能围绕木星或者火星飞行，却不能在两星之间作穿越飞行，如图3所示。

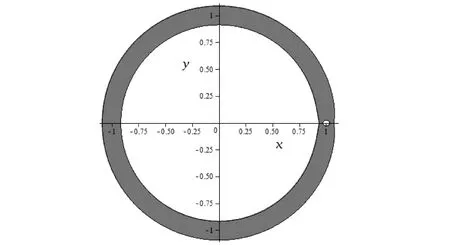
图3 航天器的零速度曲线C=3.023

当C由3.023逐渐减小时，图3中木星和火星所在的区域逐渐相互靠近。当C减小到3.019 9时，两个区域连接成了“∞”形。此时，虽然航天器的飞行区域有所增加，但“∞”形腰部的那个交叉点(0.950 359 873 1，0)，却成了航天器在木星和火星之间作穿越飞行的“要塞”，如图4所示。图4局部放大的部分如图5所示。

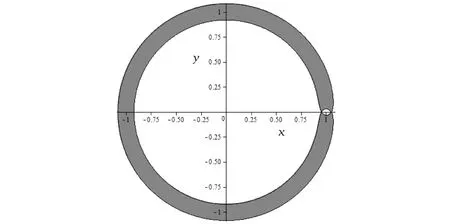
图4 航天器的零速度曲线C=3.019 9

当C<3.019 9且逐渐减小时，连接木星和火星之间飞行区域的“要塞”被打开，如图6所示，此时航天器不仅可以在木星和火星各自的区域飞行，还可以通过转移轨道从其中一个星球穿越飞行到另一个星球。

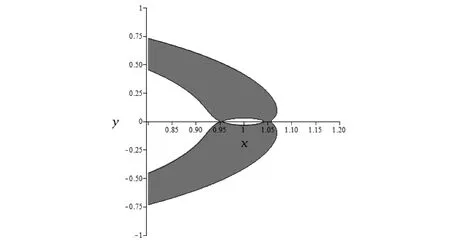
图5 航天器的局部零速度曲线C=3.019 9

图6 航天器的零速度曲线C=3.019 8

当C减小到3.019 42时，木星和火星之间“保龄球”状飞行区域与最外围的“大圆”在临界点(1.049 041 965，0)处连接在一起，演化出新的“要塞”，如图7所示，航天器仅能在“保龄球”状飞行区域内部自由活动，但不能穿越飞行到外围的宇宙空间。

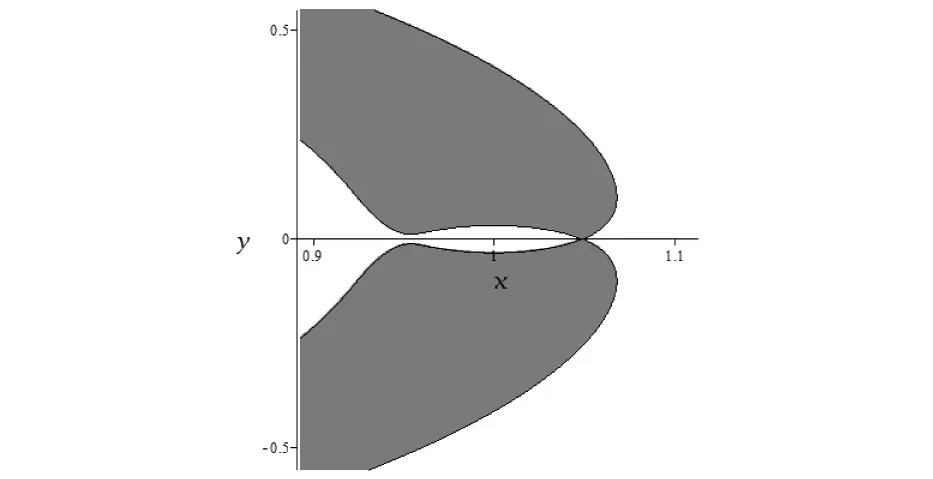
图7 航天器的零速度曲线C=3.019 42

当C继续逐渐减小时，“保龄球”状飞行区域与外围宇宙空间之间新的“要塞”(1.049 041 965，0)被打开。当C=3.019时，探测器不仅可以在木星和火星之间来回飞行，还可通过打开的新“要塞”去探索外围的宇宙空间，如图8所示。

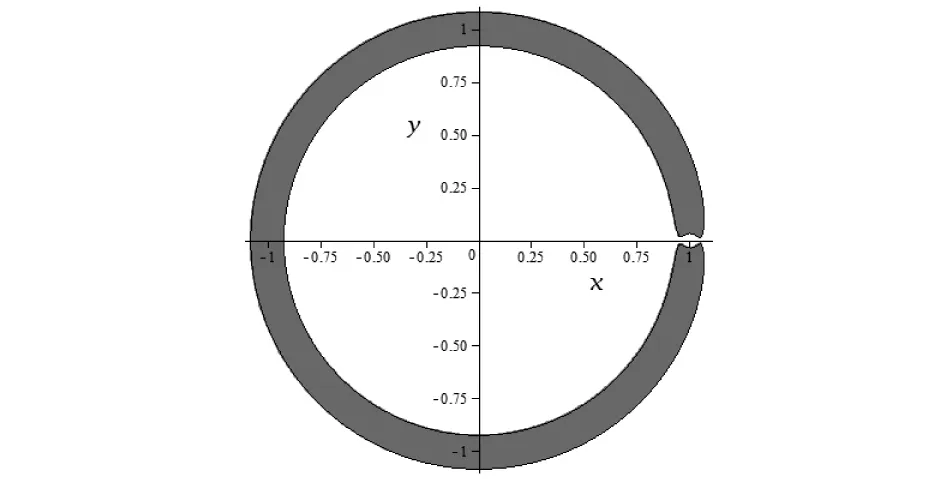
图8 航天器的零速度曲线C=3.019

当C再次逐渐减小至3.000 4时，航天器的禁飞区域已退缩至由两块弯弧状在临界点(-0.995 600 046 3，0)处连接成的区域，如图9所示。此时，航天器虽然可以通过新打开的“要塞”缺口飞向外围宇宙空间，但却不能通过两块弯弧状连接点处飞向外围宇宙空间。随着C越来越小，航天器的禁飞区域也逐渐变小，如图10和11所示。

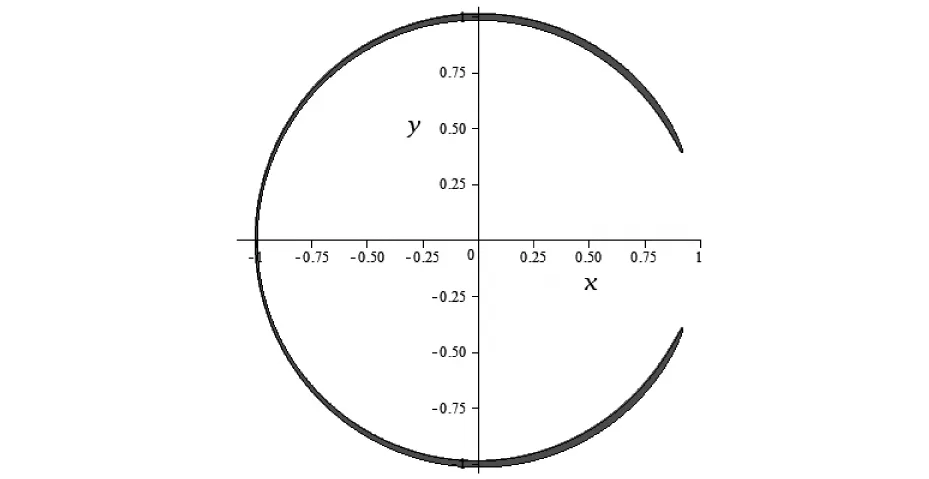
图9 航天器的零速度曲线C=3.000 4

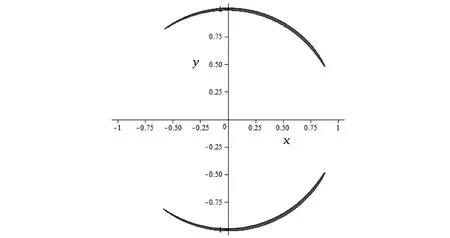
图10 航天器的零速度曲线C=3.000 1

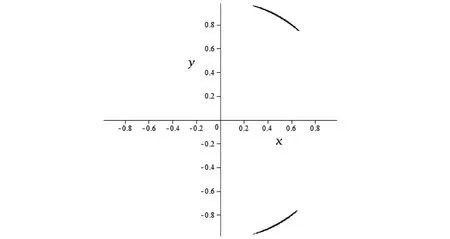
图11 航天器的零速度曲线C=2.999 7

通过上述数值模拟结果，我们发现当Jacobi常数C的值较大时，它描绘出一条远离原点且形状近于圆形的闭曲线以及两条分别围绕木星和火星的闭曲线；当C的值逐渐减小时，木星和火星附近的两条闭曲线却逐渐扩大，随后在交点处相遇，由于在交点处曲线的法线方向不确定，也就是奇点的情况，那么这个交点实际上就是平动点L1。类似地，当C继续减小时，两条闭曲线在平动点L1处融合成一条不断膨胀的闭曲线并与不断缩小的外面曲线相遇于平动点L2；当C再继续减小，里外两曲线变成一条在平动点L3处自交的闭曲线；最后，当C再度减小时，曲线分裂成上下两块，最终收缩为两个平动点L4和L5。L1，L2和L3三个平动点，它们在火星和木星的连线上，也称为共线平动点，而L4和L5这两个平动点关于坐标轴对称且分别与火星和木星组成等边三角形，也称为三角平动点[1，4，8]。

3 木星-火星之间转移轨道的数值模拟

在实际的深空探测任务中，图8是我们最为关注的情形，最具应用价值。因为如果Jacobi常数C的取值比图7中的C还大的话，航天器没有足够的能量，脱离不了火星或者木星引力的束缚；如果Jacobi常数C的取值比图9中的值还小的话，这不但意味着航天器系统需要消耗大量的能量，而且对运载火箭等也提出了更高的要求，甚至能否成功地将航天器从地球发射至火星都是个未知数。只有当Jacobi常数C的取值介于上述两种情形之间时，航天器既能飞离木星-火星系统，又不需携带额外的能量。

我们选取适当的初始条件[0.999 6，0，0，-39，-0.9，-0.12]，通过数学软件Matlab 2011a对系统(6)进行数值模拟，得到一条从火星(0.999 6，0，0)出发，最终到达木星周围(-0.000 334 5，0.002 237，-0.002 645)的转移轨道，如图12所示。

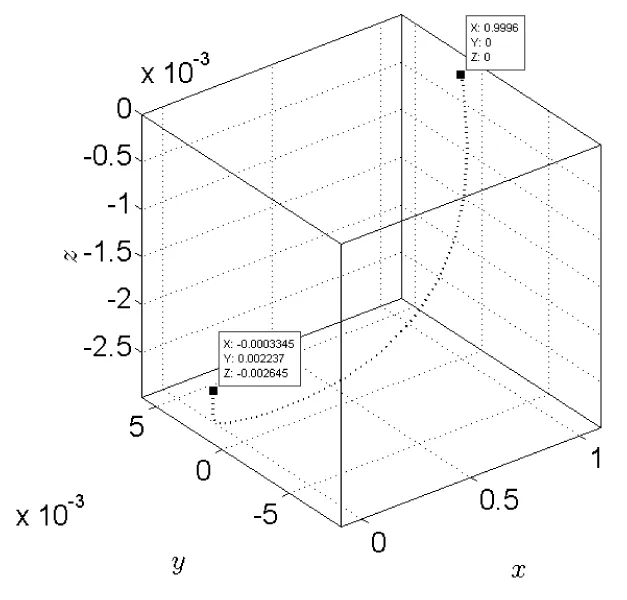
图12 火星到木星的转移轨道

4 结论

本文深入讨论了火星-木星-航天器系统的零速度曲线、零速度曲面的几何结构和Jacobi常数C的关系。结果表明：随着C的取值逐渐增大，虽然此时系统需要消耗的能量越来越小，但探测器能够飞行的区域也随之逐渐缩小；反之，随着C的取值逐渐减小，探测器能够飞行的区域也越来越大，连接火星和木星之间的禁飞区域也将首次在平动点L1处打开，此时环绕火星(木星)飞行的航天器就可以被木星(火星)捕获；或者说，火星(木星)航天器将会逃逸到环绕木星(火星)飞行的轨道上。由于C的取值越小，系统需要消耗的能量越大，对运载火箭系统的要求也越来越高，使得很多的探测任务不能实施，所以我们最希望关注的还是二者的最优情形，即根据探测器实际探测任务的飞行范围和火箭的实际运载能力，选取适当的Jacobi常数C，使得航天器的飞行范围尽可能大的同时系统携带的能量尽可能地小。因为消耗的燃料越少，飞行器的总重量也就越轻，飞行器的重量每减少1kg，不但可以使运载火箭减轻500kg，还能拓宽发射窗口，延长航天器运行的寿命。

此外，对于火星-木星-航天器系统，本文还数值模拟出一条火星和木星之间的转移轨道，该转移轨道可用于多任务轨道的设计，由于人类探测火星所积累的经验越来越多，因此将大大提高探测木星的成功率，在探测火星的同时探测木星，相对于独立探测火星和木星来说，可节约大量的财力和物力。

[1] Marchal C. The three-body problem： the restricted problem of three bodies[M]. Amsterdam： Elsevier Publishing Company，1990.

[2] Gao F B， Zhang W. A study on periodic solutions for the circular restricted three-body problem[J]. Astronomical Journal，2014，148(6)：116.

[3] Koon W S， Lo M W， Marsden J E， et al. Dynamical systems， the three-body problem and space mission design[M]. Springer，2011：32-34.

[4] 刘林，侯锡云.深空探测器轨道力学[M].北京：电子工业出版社，2012.

[5] 刘暾，赵钧.空间飞行器动力学[M].哈尔滨：哈尔滨工业大学出版社，2003.

[6] 陈杨，宝音贺西，李俊峰.木星探测轨道分析与设计[J].天文学报，2012(2)：106-118.

[7] 李俊峰，宝音贺西.深空探测中的动力学与控制[J].力学与实践，2007(4)：1-8.

[8] 徐明.平动点轨道的动力学与控制研究综述[J].宇航学报，2009(4)：1299-1313.

(责任编校：夏玉玲)

A Numerical Study of the Zero-Velocity Surface and Transfer Orbit of the Jupiter-Mars-Spacecraft System

TANG Gui-qin， GAO Fa-bao， WANG Kun， QIU Lin-fei

(College of Mathematical Science， Yangzhou University， Yangzhou 225002， China)

The authors of this paper， based on the Jupiter-Mars-Spacecraft system and the Euler Lagrange equation， established a dynamical equation of the spacecraft， carried out numerical simulation， studied the relationship between the zero-velocity surface of the system and the geometric structure of the Jacobi constant and designed a multi-task transfer orbit from Mars to Jupiter.

Jupiter； Mars； zero-velocity surface； transfer orbit； numerical simulation

O242；P135

A

1672-349X(2015)03-0008-04

10.16160/j.cnki.tsxyxb.2015.03.003