基于最优作战效能的雷达部署优化问题研究

宋佳庆,张 峰,关永胜,冯占林,张晓玲

(1.中国电子科学研究院,北京 100041；2.电子科技大学电子工程学院,成都 610054)

工程与应用

基于最优作战效能的雷达部署优化问题研究

宋佳庆1,2,张 峰1,关永胜1,冯占林1,张晓玲2

(1.中国电子科学研究院,北京 100041；2.电子科技大学电子工程学院,成都 610054)

针对反导作战场景下预警探测雷达的优化部署问题,本文提出了基于最优作战效能的优化部署方法。首先根据反导预警作战需求抽取了效能评估关键指标,在结合弹道特性以及威胁目标类型的基础上,提出了优化准则以及目标函数。为提高运算速度与运行效率,应用遗传算法实现对预警探测雷达的部署位置、阵面朝向进行优化。在Linux平台下通过QT编程,完成了雷达优化部署软件开发。在该软件上进行了仿真试验,证明了该方法的高效性与有效性。

效能评估；反导作战效能；优化部署；遗传算法；预警雷达

0 引 言

美国为了应对战略弹道导弹和战术弹道导弹威胁，从上世纪就开始了导弹防御系统设计与建设[1]，其中，弹道导弹预警系统是其重要组成部分，而远程预警雷达、地基/海基多功能雷达又是弹道导弹预警系统的关键装备，其主要任务是对来袭的弹道导弹进行早期发现、跟踪识别、威胁告警，以及对拦截打击进行效果评估，为指挥决策和拦截作战提供实时预警信息保障。如何部署和利用这些高价值的反导预警雷达成为值得关注的课题[2]。在现有文献中，已有许多关于雷达部署问题的研究，但是，大多是针对防空预警雷达的优化，主要集中于全局未知的雷达部署，主要优化目标是提高雷达网的空域覆盖面积[3，4]，而并没有将所受威胁的实际情况作为条件对雷达网的作战效能进行评估和优化，即雷达部署优化的目的不具备针对性。本文将根据反导作战对预警雷达在探测、跟踪方面的要求以及预警系统需与武器系统紧密铰链的特点，有针对性地建立效能评估指标体系[3]。根据反导作战效能最优准则，对每部雷达的部署位置和阵面朝向进行优化。本文所研究的部署优化问题是一个多目标组合优化问题，随着待部署雷达和威胁目标的数目的增加，问题的搜索空间会急剧增大，目前在实际工程当中常用的枚举法很难求出最优解。对于此类复杂问题，我们应该把主要精力放在寻求满意解上，而遗传算法能够很好的进行全局最优搜索，正是求满意解的最佳工具之一。

1 反导预警雷达系统效能分析

1.1 评估原则

为了对弹道预警雷达进行部署优化，首先要构建得到雷达优化部署的效能指标，然后根据指标构建目标函数。效能评估指标应尽可能地体现雷达系统的实际探测能力，因此构建指标体系时应遵循以下几点基本原则[5]：

（1）重要性原则。反导预警雷达系统是一个复杂的系统，对系统进行评估时，会有很多可选评估指标，在选取评估指标时，需要考虑这些指标的关键性、评估难度等因素，取其中一部分最重要的指标作为评估指标。

（2）目的性原则。效能评估的具体任务各有不同，所以在指标的选择过程中，要根据评估的实际目的，有针对性地选择指标。

（3）低相关性原则。有些指标之间存在相关性，在选择指标时应尽量做到，指标之间相互独立。

（4）敏感性原则。评估指标应该对系统效能的变化足够敏感，指标值应能反映出系统的变化。

（5）可行性原则。系统指标值可以被量化，能进行定量分析。

1.2 评估方法

从1990年代开始，系统分析评估领域出现了一系列新观点、新方法以及相应的实践和应用，其中比较有代表性的包括模块化指挥控制评价结构（MCES），面向任务方法（MOA），网络中心战概念框架，信息优势价值链等[6]。通过分析，系统效能评估方法大致可分为三类：解析法、仿真法和统计法。

（1）解析法

解析法的特点是根据描述效能指标与给定条件（常常是低层次系统的性能指标、单项效能指标及作战条件）之间的函数关系的解析表达式计算指标值。这个解析表达式可以是基于军事运筹理论，也可以基于数学方法求解所建立的效能方程。常用的方法有指数法、层次分析法、德尔菲法、模糊数学方法、灰色理论方法、ADC方法、军事运筹理论等。解析法的特点是公式透明性好，易于理解，计算简单，且能够进行变量间关系的分析，准确把握关键因素及其对作战效能之间的变化规律，便于应用。其缺点是考虑因素少，只在严格限定的假设条件下有效。

（2）仿真法

仿真法是以计算机仿真模型为试验手段，通过在给定条件下运行模型来进行作战仿真试验，由试验得到的关于作战过程和结果的数据可直接或经过统计处理后，给出效能指标评估值。仿真法可以较详细地考虑影响作战过程的诸因素，因此很适合于武器系统或作战方案的效能指标的预测评估。仿真法对于武器系统效能的评估具有不可替代的重要作用。但是这种方法建模难度大、编程任务重、实验周期长，而且当涉及因素特别多时，很难准确把握关键因素及其对作战效能指标的变化规律。

（3）统计法

统计法的特点是应用数理统计方法，依据实践、演习、试验获得的大量统计资料评估效能指标。统计法应用的前提是所获统计数据的随机特性可以清楚地用模型表示并相应地加以利用。相对来说，统计法是比较可靠和令人信服的效能评估方法，但其前提条件是必须有武器系统实体参与才能进行，而且试验代价昂贵，适用于武器系统单个效能指标的评估，很难获得所有因素对效能的影响规律。对于目前正在设计中的BMDS网络中心战体系效能评估，统计法就只能待体系建成后才能进行实战检验和效能评估。

根据本文实际情况，采取解析法对反导预警雷达部署的效能进行评估，采用层次分析法确定指标权重。

1.3 效能评估指标的选择

反导预警雷达系统的综合效能是多方面的，靠单一的指标无法全面衡量，需要建立一套评价体系来进行作战效能分析与评估。指标体系由若干具体、可测、可衡量的指标组成，其中所含指标应从作战效果角度出发基于效能的原则进行选择，力求全面地表征系统的作战效能[7]。

由于本文研究雷达优化部署的主要目的是对系统在目标来袭的不同阶段所具备的能力进行优化，因此要求雷达系统在探测初期应具备及时及发现目标的能力，在发现来袭目标之后，应能对来袭目标进行持续稳定跟踪并最终引导拦截武器对目标进行拦截。于是雷达优化部署的目的可具体体现在提高雷达探测系统对来袭目标的及时发现能力、稳定跟踪能力、引导拦截能力，即在对雷达进行部署时应遵循早期发现、稳定跟踪、有效支持作战的原则。

本文研究优化部署的对象是雷达的部署位置和朝向，在选取指标时应尽量选择受雷达部署位置和朝向变化影响较大的指标作为评估指标，并假设其它指标符合作战需求，且不随雷达部署的变化而发生明显变化或者与已选择指标存在较强相关性。

反导预警雷达系统的主要任务就是早期发现、稳定跟踪、对作战的有效支持，因此，其评价指标的选择应能反映这种任务要求，通过分析，选取预警时间，生命周期跟踪比率，火控支持时间三个最为关键的指标对反导预警雷达系统进行评估，其中预警时间体现了系统的及时发现能力，生命周期跟踪比率体现了系统的稳定跟踪能力，火控支持时间体现了系统的引导拦截能力。

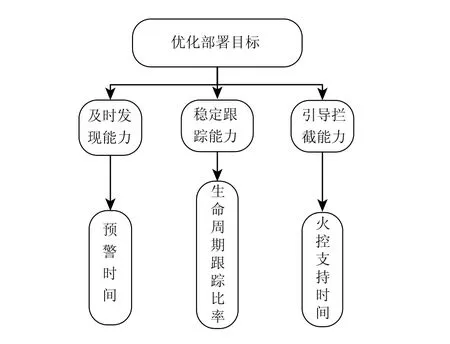
图1 优化部署评估的主要指标

要进行效能指标的综合评估，首先要将各项指标进行量化。在各项指标都可量化后，由于这些指标的量纲和函数关系不同，仍不具有可比性，需要进行归一化处理。本文以根据反导预警雷达系统的实际情况，对各项指标进行归一化处理。各指标的定义和量化方式如下：

（1）预警时间

预警时间定义为目标首次进入雷达系统探测范围到目标落地的总时长，该指标越大则可表明雷达系统能够越早发现来袭目标。

若T0为雷达系统发现目标的首点时间，导弹从发射到落地的时间为T，则预警时间为：

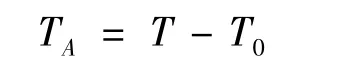
归一化后的值NPc为：

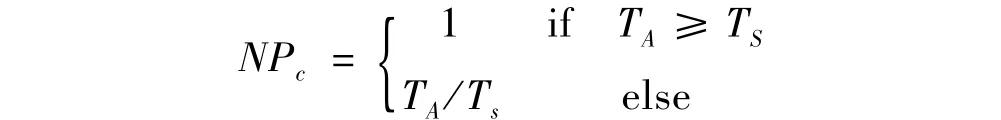
其中TS为系统战技指标对预警时间的要求值，具体范围如下：

射程小于900 km的弹道导弹的预警时间为5 min；射程小于3 500 km的弹道导弹的预警时间为8 min；射程大于3 500 km的弹道导弹的预警时间为10 min。

（2）生命周期跟踪比率

生命周期跟踪比率的定义为从雷达系统对威胁目标跟踪的总时长占导弹从发射到落地的总时长的比例。该指标值越大表明目标整个生命周期内处于被雷达监视状态的比重越大，即雷达能更好地实现对目标的稳定跟踪。

若T0为预警系统发现目标的首点时间，T1为探测到目标的末点时间，导弹的生命周期为T，则生命周期跟踪比率Pc为：

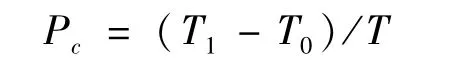
则归一化后的值NPc为：

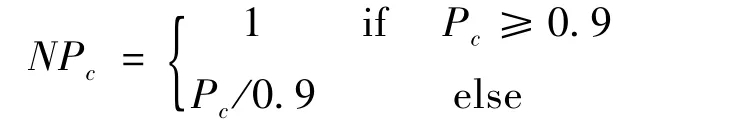
（3）火控信息支持时间

火控支持时间表示目标首次进入负责引导拦截武器进行拦截的雷达的探测范围到目标落地的时长，该指标越大，则雷达能更好地引导拦截武器对来袭目标进行拦截。

若雷达首点发现目标的时刻为Tx，来袭导弹从发射到落地的时刻为T，则火控信息支持时间为：

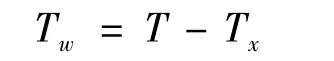
归一化方法为：

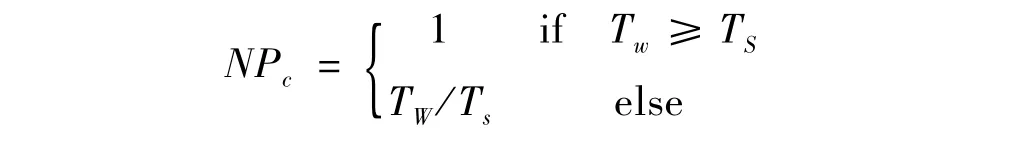
其中TS为系统战技指标对火控信息支持时间的要求值，具体范围如下：

射程小于900 km的弹道导弹的预警时间为2 min；射程小于3 500 km的弹道导弹的预警时间为3min；射程大于3500 km的弹道导弹的预警时间为5min。

基于不同的作战场景和作战任务，考虑到各效能指标的重要程度不同，需要对各项指标进行合理选取，建立加权系数。记雷达系统对某条弹道的归一化预警时间值为Ta，指标权重为wa，归一化生命周期跟踪比率值为Tc，指标权重为wc，归一化火控支持时间值为Tf指标权重为wf，则雷达系统对于该弹道的效能值E，公式如下：

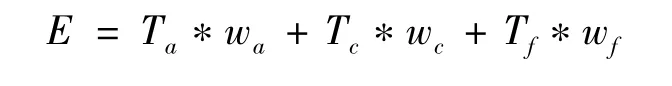
1.4 雷达部署参数与效能指标之间的关系

雷达的部署优化是要对雷达部署经度、纬度、朝向三个参数形成的组合进行优化，这三个参数的变化会对选中指标的产生较大的影响。具体以单部雷达对单条弹道的探测指标为例，如图2所示：

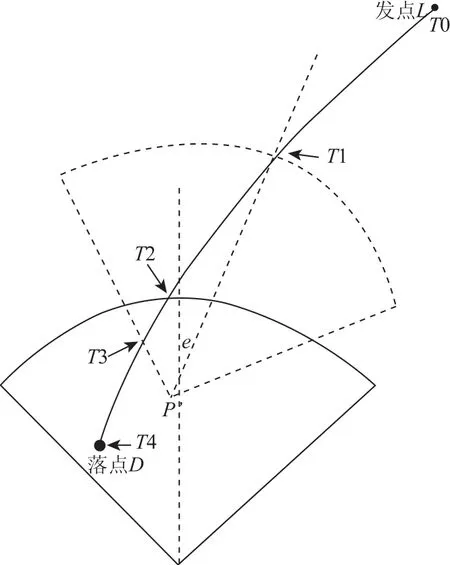
图2 雷达部署参数对指标的影响示意图

假设威胁弹道来袭导弹从L点发射，攻击目标位为D点，飞行轨迹如图所示。在此攻击场景下，假设雷达部署位置状态为P，雷达阵面朝向为0度；此时来袭目标从T2时刻起直至落地处于雷达探测范围，雷达对来袭弹道的预警效能指标值如下：

预警时间为：TA=T4-T2；

生命周期跟踪比率Pc为：Pc=（T4-T2）/（T4-T0）；

假设雷达具有制导功能则雷达的火控支持时间为：Tw=T4-T2。

此时若雷达的部署位置和朝向参数发生变化，如图所示，雷达部署状态变化到Pˊ，阵面朝向顺时针增加Θ，则雷达效能评估指标值将发生明显变化，来袭目标从T1时刻起进入雷达探测范围，雷达对来袭目标的预警效能指标变化如下：

预警时间为：TA=T4-T1；

生命周期跟踪比率Pc为：Pc=（T3-T1）/（T4-T0）；

火控支持时间为：Tw=T4-T1。

钢管桩采用地质钢管(YB235-70 DZ40)，规格为D127δ4.5，桩中心距为500 mm，施工桩长9.00 m，嵌入较完整基岩深度不小于2 m。采用工程钻机回转钻进法(干成孔)成孔后植入钢管，严禁潜孔锤法成孔，成孔孔径不小于130 mm(D127)。钢管内灌注M30纯水泥浆，桩位偏差不应大于50 mm，垂直度偏差不应大于1.0。钢管桩嵌岩段分层开孔，以便钢管桩与土(岩)层间隙灌注M30水泥浆密实，灌注过程中应防止钢管浮动。

多部雷达的部署参数的变化对系统效能指标值得影响更为复杂，且为非线性关系，但原理与单部雷达单条弹道的关系相似，可见已选的雷达系统效能评估指标值受雷达参数影响较大可作为雷达优化部署的目标函数。

2 遗传算法

遗传算法直接对结构对象进行操作，不存在求导和函数连续性的限定，具有内在的隐并行性和很好的全局寻优能力，适用于求解雷达部署优化问题[4]。

2.1 约束条件

根据本文研究问题的实际情况，对于反导预警雷达系统的雷达部署做如下假设：

（1）为了便于应用极坐标进行遗传编码，假设每部雷达的可部署位置限定为圆形区域；

（2）待部署雷达的性能参数和数量已知；

（4）假设雷达系统中各装备之间能够良好衔接。

2.2 染色体编码设计

根据雷达部署约束条件，待部署雷达部署在给定的圆形可部署区域内，即以某一点（Plon，Plat）为圆心，R为半径的圆形区域。将雷达部署位置的经纬度坐标（Rlon，Rlat）转换为以可部署区域中心点为极点的极坐标（r，θ）表示，则极轴r的取值范围应为[0，R]（单位：公里），极角θ的取值范围应为[0，360]（单位：度），雷达朝向O为雷达阵面法线与正北方向的顺时针旋转角度，取值范围应为[0，360]（单位：度）。由（Plon，Plat）和（r，θ）可确定雷达部署位置的经度和纬度表示，公式如下：

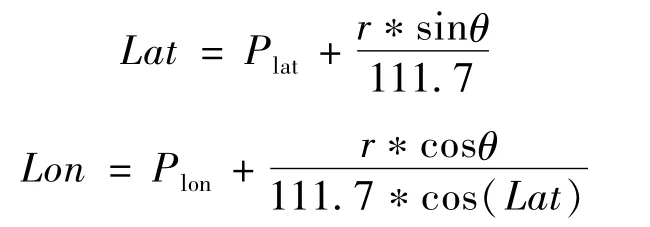
设待部署雷达数量为M，将每部雷达相对于可部署区域中心点的极角、极轴、以及朝向作为遗传基因编码。编码形成的染色体串对应着一种雷达部署方案。染色体基因包括雷达位置的极坐标表示（r，θ）和雷达朝向O，图中每一个单元格代表雷达部署的一个参数，编码方法如图3所示：

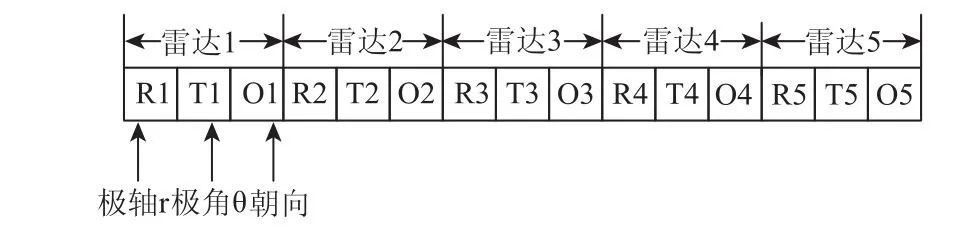
图3 染色体编码方法

2.3 适应度函数

适应度值是计算适应度函数所得到的值，它的大小是遗传算法中更新个体极值和全体极值的依据。适应度函数是根据具体问题设计的，通常在目标函数并不特别的情况下，可以直接将目标函数选择为适应度函数[4]。在设计雷达优化部署模型时，适应度函数是算法的核心，在雷达组网部署优化的过程中，适应度函数是优化搜索的判决条件，是运算量中最大的环节。对于一个具体的应用背景，根据实际作战任务要求的不同，适应度函数的选择各不相同。

假设来袭弹道数量为K，确定每条弹道的威胁权重为mi，每条弹道的预警探测效能值为Ei，则适应度函数可定义为：

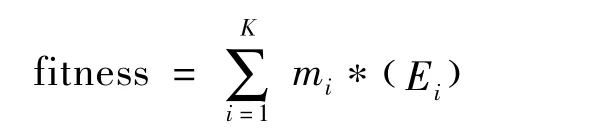
本文研究地面雷达部署问题，所以需要利用地理信息系统对雷达部署位置是否在陆地上进行判断，有函数如下：

如果部署方案中存在雷达部署位置不在陆地，则对该方案的适应度值进行惩罚。假设有M部待部署雷达，则调整适应度函数如下：

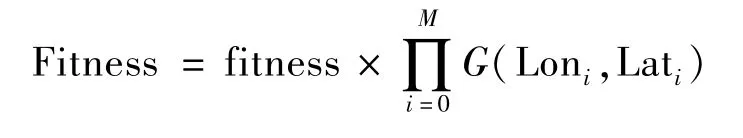
2.4 遗传操作

基于遗传算法的组网雷达优化部署算法流程如图4所示。

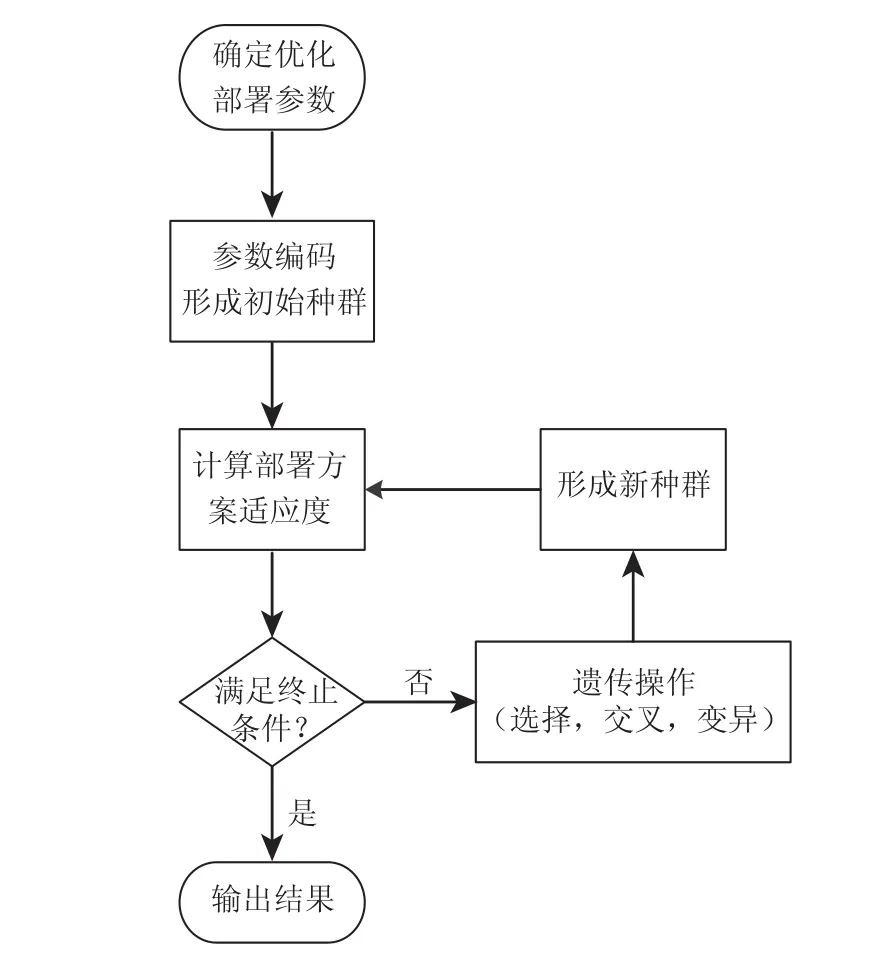
图4 优化部署算法流程

遗传操作具体流程如下：

根据雷达部署约束条件随机生成M部雷达的部署位置，每部雷达的部署位置和朝向即为一个基因组编码，M部雷达的部署就可以形成一个染色体串。假设每一代种群个体数为N，则随机生成N个满足约束条件要求的部署方案，用这N种部署预案组成遗传算法的初始种群。

以适应度为选择原则，选择种群中出适应度高的部署方案传给下一代，淘汰适应度低方案。同时为满足遗传算法收敛的要求，保证最优个体能够被复制到下一代，应当将当代适应度最高的个体替换下一代个体中适应度最差的个体，以保证适应度最高的个体能够存活到下一代种群中。

以交叉概率Pc随机不重复的从中间群体中选择两两个体对，等概率随机选择个体对中的基因交换位，对交换位前的基因进行交叉运算以变异概率Pm对所有个体的进行变异运算，随机产生一个符合限制条件的数赋值给变异位，生成子代种群，需要注意的是，变异生成的新个体也必须满足雷达部署的约束条件。

将经过选择，交叉，变异形成的子代种群替换父代种群，继续循环进行遗传操作，直至满足停止条件。

3 实例分析

工程上已经在Linux平台下通过QT编程，完成了雷达优化部署软件开发。应用已开发完成的软件系统进行实例分析如下：

3.1 想定场景

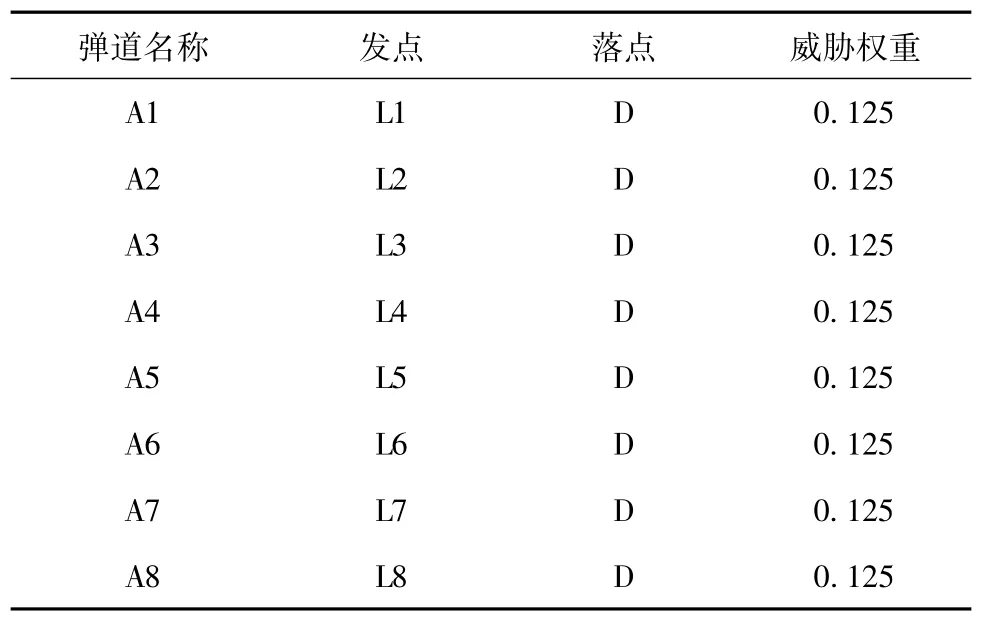
表1 攻击场景参数表

假设某地区受到表1中弹道导弹的威胁，其中威胁权重是综合考虑了攻击场景的威胁程度，可能发生的概率等综合因素考虑的归一化的值，可以通过专家打分法获得，这里简单假设弹道权重相等。攻击场景如图5所示。

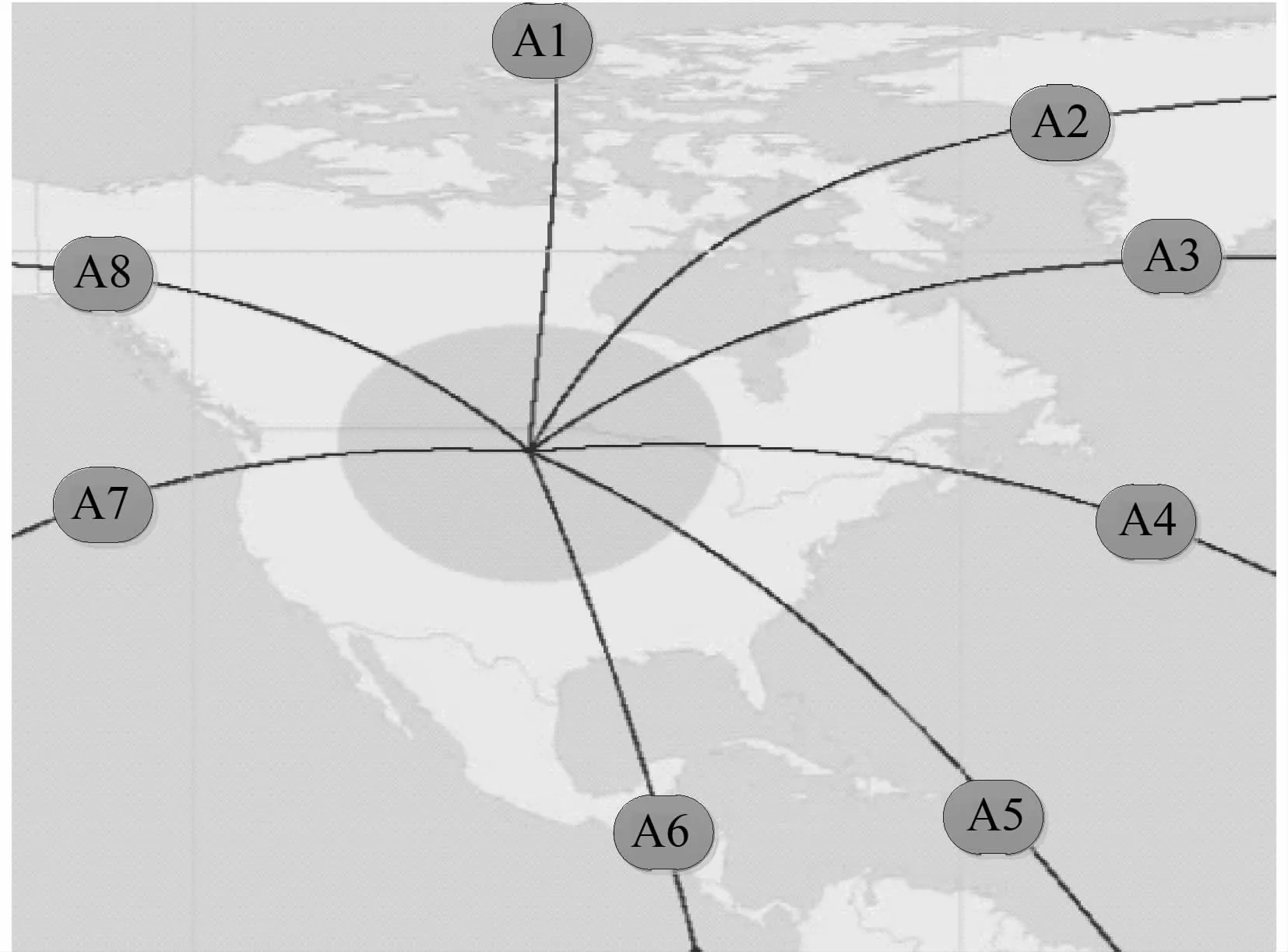
图5 想定攻击场景图

假设现有A和B两种型号的雷达可部署，A雷达同时具有引导拦截武器进行拦截和探测来袭目标的能力，B雷达只具备探测来袭目标的能力，并且A和B雷达之间可以进行良好交接。雷达可部署区域为以受攻击点D为圆心，半径为1200 km的圆形区域。两种型号雷达参数如表2所示。

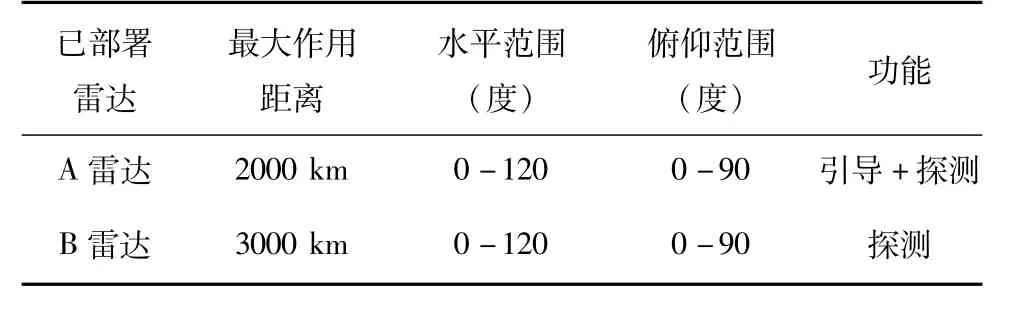
表2 待部署雷达参数表

设定如表3所示的效能评估指标权重：

表3 指标及其权重表

3.2 遗传算法优化结果

由于雷达资源有限，所以在部署时应使用尽量少的雷达来满足作战需求，考虑首先采用表1中雷达作为方案1进行雷达部署。

表4 待部署雷达表（方案1）

对A和B雷达的部署进行优化后得到结果如图6所示：

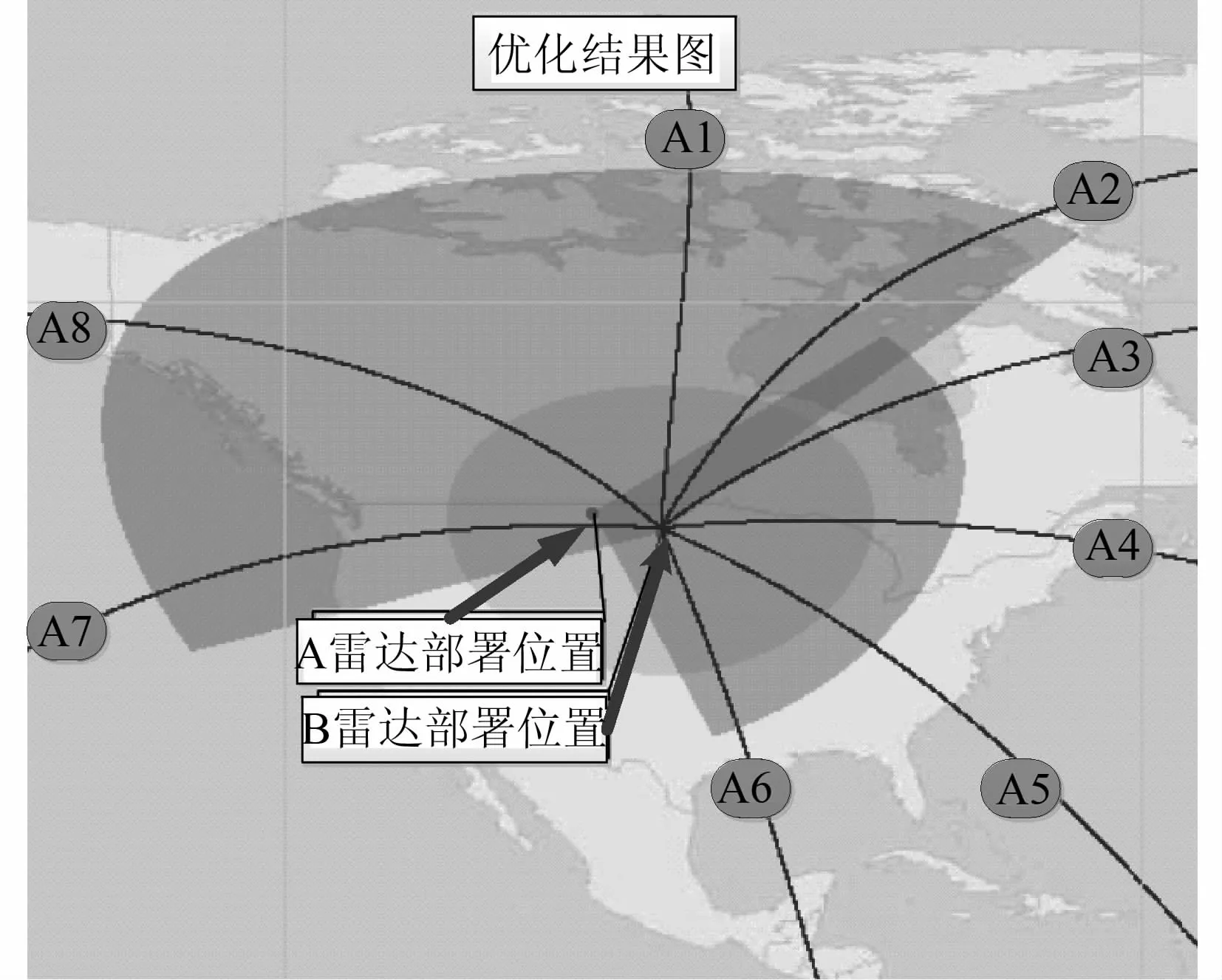
图6 优化部署结果图（方案1）

每条弹道的指标值如表5所示。

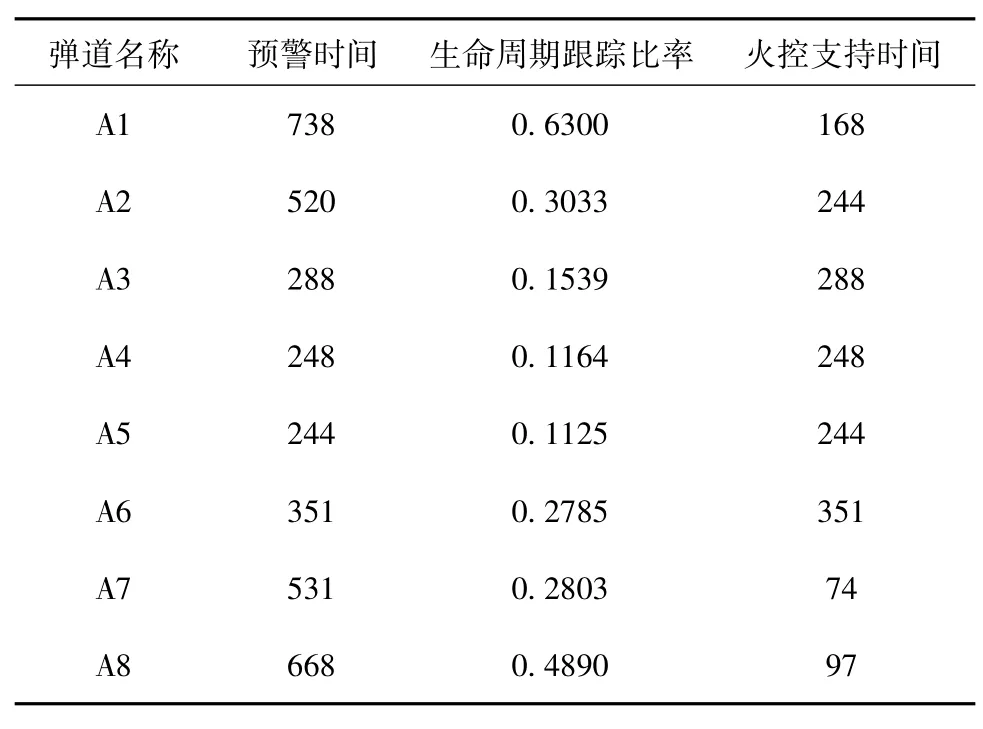
表5 弹道指标值表（方案1）

方案1的系统作战效能值为：0.6321。

通过分析发现，部署方案1对弹道A1，A7，A9三个来袭目标的火控支持能力不足，需要增加A雷达以提高拦截支持能力，对A3，A4，A5三个来袭目标的及时发现能力不足，需要增加B雷达以提高尽早发现能力。

通过多次仿真验证发现，部署3部A雷达2部B雷达之后继续加入新的雷达对雷达系统的效能的增加不再明显。

因此采用表2中的雷达作为方案2进行优化部署。

表6 待部署雷达表（方案2）

因此对于该攻击场景而言，需要部署3部A雷达和2部B雷达，对各个雷达的部署位置和朝向进行优化后得到结果如图7所示。

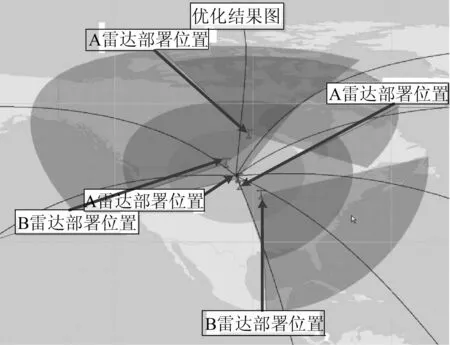
图7 优化部署结果图（方案2）

每条弹道的指标值如表7所示。

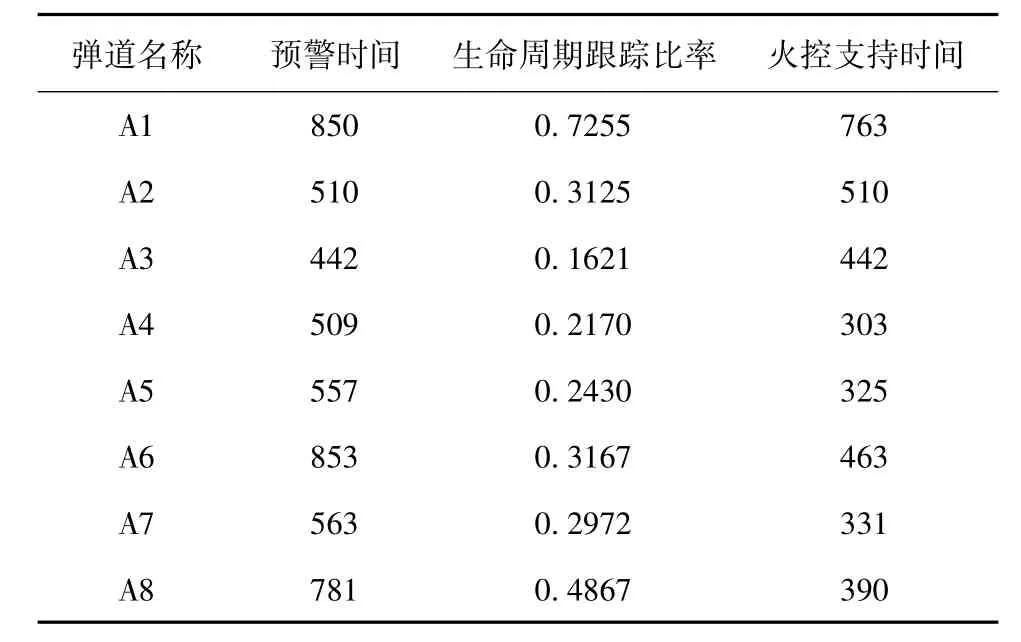
表7 弹道指标值表（方案2）

方案2的系统的效能值为：0.8416。

通过实例证明，遗传算法能够对反导预警雷达系统的雷达优化部署问题进行求解。另外，遗传算法同时对搜索空间中的多个解进行评估，避免了陷入局部最优的风险，同时算法本身易于实现并行化，所以遗传算法可以比较快速准确地求解出作战效能最优的雷达部署方案。

3.3 仿真结果对比及分析

在实际工程中对部署方案的优化多采用枚举法。本文通过仿真实验使用枚举法对上文中方案2的部署进行优化，枚举法首先要对待部署区域进行栅格化分割，仿真假设栅格经度精度为0.1（单位：度），纬度精度为0.1（单位：度），雷达朝向变化精度为10（单位：度），并通过预先处理剔除位于部署范围以外的点，然后对所有可能的方案的效能值进行计算，从中选择作战效能值最优的方案作为最优部署方案，遗传算法和枚举法两种方法的结果对比如表8所示。

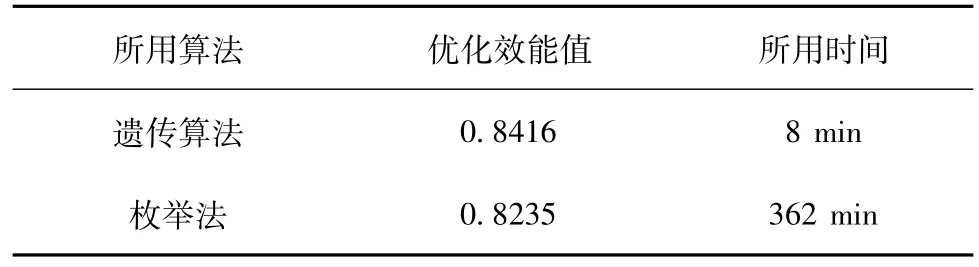
表8 遗传算法与枚举法优化结果表

从上表可以看出，由于枚举法对部署区域进行了离散分割，计算出的方案效能值稍差于遗传算法。另外由于枚举法自身的特性，随着待部署雷达数量的增加，在栅格精度不变的情况下，搜索空间会急剧增大，使得计算时间变得很长，因此枚举法不适合求解复杂的部署方案。通过以上对比可以发现，遗传算法可以更加快速准确的求得最优解。

4 结 语

本文针对基于效能最优的雷达部署优化问题进行研究，根据需要，抽取出了反导预警作战效能关键指标，并提出了通过基于遗传算法对雷达的部署位置和阵面朝向的优化方法。通过仿真实验表明，遗传算法可以应用于基于作战效能最优的雷达部署优化中，并且可以较快的计算速度，能够很快地逼近最优或者次优解。该方法已经在某工作中得到很好的应用。

[1] 张昌芳，朱启超，匡兴华.美国弹道导弹防御C2BMC系统发展综述[J].装备学院学报，2012，23（3）：60-63.

[2] 刘兴，赵敏.一体化空天防御系统及其技术[M].北京：国防工业出版社，2011.

[3] 刘健，姚澎涛，罗亮.早期预警雷达部署要求探讨[J].航天控制，2014，32（4）：91-95.

[4] 张远，方青，曲成华.基于遗传算法的组网雷达优化部署[J].雷达科学与技术，2014，12（1）：76-80.

[5] 李滨辉，陈明珣，钱建刚.基于灰色AHP的海军要地防空预警效能评估[J].海军航空工程学院学报，2011，26（1）：101-104.

[6] 童志鹏.综合电子信息系统[M].北京：国防工业出版社，2008.

[7] 吴红兵，王鹏.C4ISR系统效能层次化评估方法研究[J].中国电子科学研究院学报，2009，14（2）：205-210.

宋佳庆(1991—),男,硕士,主要研究方向为雷达信号与信息处理方向；

E-mail：haierdy@163.com

张 峰(1986—),男,博士,主要研究方向为电子信息系统总体设计；

关永胜(1979—),男,博士,主要研究方向为电子信息系统系统总体设计、雷达自动目标识别；

冯占林(1963—),男,吉林通榆人,研究员、博士,研究方向为电子信息系统设计、综合集成、系统分析与评估；

张晓玲(1964—),女,教授,博士生导师,主要从事合成孔径雷达(SAR)处理技术、ISAR技术、目标分类与识别技术以及卫星导航定位技术等方面的研究。

Research on Radar Deployment Based on Optimal Operational Effectiveness

SONG Jia-qing1，2，ZHANG Feng1，GUAN Yong-sheng1，FENG Zhan-lin1，ZHANG Xiao-ling2
（1.China Academy of Electronic and Information Technology，Beijing 100041，China；2.School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 610054，China）

In view of the deployment of radar detection network undermissile defense scene，a deploymentmethod based on optimal operational effectiveness is proposed.Effectiveness evaluation system is established in accordance with the application of ballistic missile defense.Considering ballistic trajectory character and target type，optimization criteria and an objective function are proposed.In order to improve the running speed and efficiency，genetic algorithm is applied to the deploymentoptimization of radars’positions and orientations.Through the QTProgramming on the Linux platform，the developmentof radar deployment software is completed.Simulating with this software，the efficiency and effectiveness of the proposed method is proved.

effectiveness evaluation；missile-defense operational effectiveness；deployment optimization；genetic algorithm；early warning radar

E956

A

1673-5692（2015）04-372-08

10.3969/j.issn.1673-5692.2015.04.008

2015-05-25

2015-07-29