Low-Delay Loop Detection Algorithm for LDPC Codes

2015-06-23MAKexiangZHANGPeng

中国电子科学研究院学报 2015年4期

MA Ke-xiang，ZHANG Peng

（1.China Academy of Electronics and Information Technology，Beijing 100041，China；2.Communication Network Center，Northwest Regional Air Traffic Management Bureau of CAAC，Xi'an 710082，China）

基础理论

Low-Delay Loop Detection Algorithm for LDPC Codes

MA Ke-xiang1，ZHANG Peng2

A low-delay loop detection algorithm for bit-flipping based iteration LDPC decoding is proposed.By introducing the concept of loop characteristic，only the iteration steps with loop characteristics are detected and labeled for the subsequent loop detection.As a result，computation delay is greatly reduced.Furthermore，the position vector for the selected iteration steps is also established to implement loop detection for these iteration steps，which reduces the hardware cost of the loop detection aswell.The validity of the proposed algorithm is verified by simulations.

loop characteristics；low delay；position vector；parallel

1 Introduction

Low-density parity-check（LDPC）codes[1]，were first proposed by Gallager in the 1960s and later resurrected by MacKay and Neal[2].LDPC has attracted considerable attention due to its near Shannon-limit performance and inherently parallelizable decoding structure[3].There have been two main kinds of algorithms to decode the LDPC codes，belief-propagation（BP）-based algorithm and bit flipping（BF）-based algorithm.BP-based algorithms have been extensively applied for its great decoding performance，especially normalized min-sum algorithm and offsetmin-sum algorithm.Because of their high computational complexity，however，the implement of the BP-based decoder is limited to the hardware resource to some extent，especially thememory resource[4].

Compared with belief-propagation based decoding algorithms，bit-flipping（BF）based LDPC decoding algorithms，e.g.，weighted bit-flipping（WBF）[5]，can achieve a better tradeoff between the error-correcting performance and decoding complexity.In the process of BF-based decoding，however，some bits may be flipped back after several iteration steps，which may result in an infinite loop.To solve this problem，loop detection algorithm[6-8]is proposed to eliminate the invalid iterations.Nevertheless，since the existing algorithms can only be performed in an iterativeway，the inherent high computing delay limits their practical implementations for high-data-rate communication systems[9].

A low-delay loop detection algorithm for the BF-based decoding is proposed by introducing the concepts of loop-characteristic and position vector.The computation delay ismainly reduced by determining the iteration stepswith loop-characteristics.For the subsequent loop detection，the hardware cost of loop detection can be reduced by establishing the position vector of flipped bits for the selected steps.

2 Proposed Algorithm

An LDPC code is a linear block code given by the null space of a“sparse”parity-check matrix H，and“sparse”means that the number of zero entries is much greater than that of the non-zero ones in the parity-check matrix.An LDPC code is defined as a（dv，dc）-regular code if its parity-check matrix has exactly dv“non-zero”entries in each row and dc“non-zero”entries in each column.

A binary LDPC code c=[c1c2…cN]with length N and dimension M is considered.An arbitrary codeword c is transmitted over the AWGN channels and BPSK modulated.It is mapped to s= [s1s2… sN] by sn=1-2cnbefore transmission. The received vector，the initial binary hard-decision vector and the corresponding parity-check matrix are denoted by y=[y1y2… yN]z0= [z1z2… zN]and H=[hMN]，respectively. zk（0＜k≤Kmax）represents the tentative binary harddecision vector at the end of the k-th decoding iteration and Kmaxis themaximum number of the decoding iterations.Theweightof the syndrome vector sk=zk×HTis denoted by wk.

a）Loop-Characteristic and Position Vector

In essence，a loop appears at the k-th iteration if and only if

Tab le I Key parameters in the decoding process at different SNR

zk=zk0（0≤k0＜k）·As a result，the weights wkand wk0of the corresponding syndrome vectors become equal.If wk=wk0，we say that the k-th tentative binary hard-decision vector zkhas a loop-characteristic.It should be noted that，wk=wk0is only a necessary condition for the appearance of a loop.Hence，further work should be carried out to check whether a loop really appears.

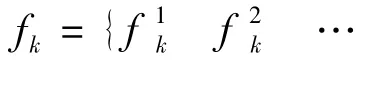
b）Proposed Algorithm

The proposed algorithm consists of two major steps：

Step 1：Loop-characteristic detection

To detect the loop-characteristic of the tentative binary hard-decision vectors zkat the end of k-th iteration step，the weight of current syndrome vector is computed and compared with the weights of all previous syndrome vectors.When any two weights become equal，a loop-characteristic is detected.Note that wk=wk0is only a necessary condition for zk=zk0. Hence，loop detection must be implemented for these iteration stepswhich have loop characteristics.

Step 2：Position vector based loop detection

3 Delay and Hardware Cost Analysis

In the existing algorithms，loop detection between the current iteration and any previous iteration is performed in an iterative way at the end of each iteration. By denotingk as the average number of iterations，ithas been shown that the average computational delay of loop detection for some received vector is（k+1）·k ·ο（ω）/2，whereο（ω）①ωis the number of the total flipping positions in one iteration[7] [8].is the computational delay which is required to detectwhether a loop appears between two iterations.Because loop detection can only perform sequentially[7]-[8]，itwill result in a remarkable increase in the decoding delay.

For the proposed algorithm，the computational delaymainly results from loop-characteristic detection and position vector based loop detection.For loop-characteristic detection，the weight wkshould be compared with each previousweight，but it can be performed by k comparators in a parallelway.Hence，the loop-characteristic detection only requiresk clock cycles in total. The number of the error bits in the decoding process is consistently varying，and then wkwill be varying simultaneously[10].Thus，the average numberτof the iterations with loop characteristic is very small.Consequently，most iterations are not involved into loop detection.As a result，the computational delay of the proposed algorithm mainly depends on the loop-characteristic detection.From the analysis above，we conclude that the computation delay of the proposed algorithm（（k-+τ·ο（ω）））is much lower than that of the previous algorithms（（k-+1）·k-·ο（ω）/2）·

The hardware cost of the proposed algorithm is analyzed as follows.Since dk0→kis a P-dimension vector，the hardware cost of loop detection based on position vector isο（P）（ο（N）for the previous algorithm[7]-[8]）.In the common communications systems，most bits in some N-dimension received vector can be correctly demodulated.Moreover，only a small fraction of the correct bitswould be wrongly flipped in the process of BF-based decoding，hence P is usually smaller than N.Correspondingly，the hardware cost of loop detection based on position vector is reduced.

4 Simulation Analysis

Here，different parameters in the decoding process for the proposed algorithm are provided.Type-I（1023，781）EG-LDPC code with the WBF-based LDPC decoding algorithm in[8]is adopted and the maximum number of the decoding iterations is50.Moreover，an AWGN channel with zero mean and variance N0/2 and BPSK modulation are considered.For each SNR，the number of the trialed codeword is 105.

Tab.I shows the average numbers of loops and loop-characteristics appearing in the iterative decoding process of the 105received vectors at different SNR，as well as the average iteration number（k-）and the average length of position vector（P-）.From Tab.I，we can see that，the average number of iteration stepswith loop-characteristics is only 0.04 in the iterative decoding process at4.2 dB.Moreover，the number of iteration stepswith loop-characteristic is gradually reduced with an increase in the SNR.Hence，most iterations only involve the loop-characteristic detection（actual loop-detection is unnecessary）.This means the processing delay of the proposed algorithm is relatively low.We also notice that the maximum average length of position vector appears at4.0 dB，which is equal to 1/40 of the codeword length N（=1023）.Therefore，the hardware costο（P）of the position vector based loop detection is smaller than that of the existing loop detection algorithms（ο（N））·

5 Conclusion

We propose a low-delay loop detection algorithm. Based on the concepts of loop characteristic，loop detection is only implemented for a small fraction of iterations，which greatly reduces the processing delay of the loop detection.Compared with the existing algorithms，the proposed approach has a lower processing delay and hardware cost.Simulation results verify the efficiency of the propose algorithm.

[1] GALLAGER R.Low-density Parity-check Codes[J].Information Theory，IRE Transactions，1962（8）：21-28.

[2] MACKAY D JC，NEAL R M，Near Shannon Limit Performance of Low Density Parity Check Codes[J].Electronics Letters，1997（33）：457-458.

[3] LI ZW，et al.Efficient Encoding of Quasi-cyclic Lowdensity Parity-check Codes[J].Communications，IEEE Transactions，2006（54）：71-81.

[4] CHEN X H，et al.Memory System Optimization for FPGA-Based Implementation of Quasi-Cyclic LDPC Codes Decoders[J].Circuits and Systems I：Regular Papers，IEEE Transactions，2011（58）：98-111.

[5] LIS，JR D JCOSTELLO.Error Control Coding：Fundamentals and Applications[J].2nd edition，Prentice-Hall，Upper Saddle River，NJ，2004.

[6] LIG，FENG G.Improved Parallel Weighted Bit-flipping Decoding Algorithm for LDPC Code[J].Communications，IET，2009（3）：91-99.

[7] NGATCHED TM N，et al.An Improved Decoding Algorithm for Finite-geometry LDPCCodes[J].IEEE Trans. Commun，2009（57）：302-306.

[8] LIU Z，PADOSD A.A Decoding Algorithm for Finitegeometry LDPCCodes[J].IEEE Trans.Commun，2005

曾勇虎(1972—),男,江西龙南人,博士,研究员,主要研究方向为电子信息系统建模仿真与评估、复杂电磁环境模拟构建及效应；

蒙洁(1972—),女,广西藤县人,硕士,高级工程师,主要研究方向为电子信息系统效能评估理论。（53）：415-421.

[9] MILADINOVIC N，FOSSORIER M P C.Improved Bitflipping Ddecoding of Low-density Parity-check Codes [J].Information Theory，IEEE Transactions，2005（51）：1594-1606.

[10]CHO J，SUNGW.Adaptive Threshold Technique for Bit-Flipping Decoding of Low-Density Parity-Check Codes [J].IEEE Commun.Lett，2010（14）：857-859.