一种新型垂尾抖振抑制方法实验研究
2015-06-23华如豪叶正寅
张 庆, 华如豪, 叶正寅
(西北工业大学 翼型叶栅空气动力学国防科技重点实验室, 西安 710072)
一种新型垂尾抖振抑制方法实验研究
张 庆, 华如豪, 叶正寅
(西北工业大学 翼型叶栅空气动力学国防科技重点实验室, 西安 710072)
现代高性能三角翼/双垂尾布局战斗机的垂尾结构普遍受到严重的非定常抖振载荷的困扰。根据自诱导理论提出了一种新型的垂尾抖振抑制方法,利用机头处的静态或振动式硬质鼓包,使三角翼前缘涡涡核弯曲、扭转,从而改变前缘涡的轨迹,延缓涡的破裂,减弱前缘涡破裂尾迹在垂尾周围流场处的脉动强度,以达到抑制垂尾抖振的目的。在西北工业大学低湍流度风洞实验室进行了风洞实验,实验所用模型为一个铝制的全机模型,该模型由一个70°大后掠的三角翼,以及两个31°后掠的垂尾组成。风洞内实验段的风速为10m/s以及20m/s,迎角范围为20°~50°。实验目的是测量机头处的静态或振动式球形鼓包对垂尾抖振的抑制效果。在尾翼根部两侧粘贴有半桥连接的应变片,用以测量尾翼根部的应变,以此应变作为尾翼抖振强度的衡量标准。实验结果表明,不论是静态的还是振动式的鼓包都不同程度地减缓垂尾的抖振响应,振动式鼓包对垂尾的抖振抑制效果与鼓包的振动频率有关。某一侧的鼓包仅对该侧的垂尾抖振有抑制效果,它不影响另一侧垂尾的抖振响应。频谱分析的结果表明,鼓包在抑制垂尾抖振的同时并没有改变垂尾振动的主频。
机头鼓包;大后掠三角翼;前缘涡;自诱导理论;抖振抑制
0 引 言
大后掠三角翼/双垂尾气动布局是现代高性能战斗机经常采用的一种布局形式,此类战斗机依赖强涡流来产生大迎角操纵所需的高升力。即使在极限高度和极限飞行条件下,三角翼前缘卷起的涡流仍会在上翼面产生强吸力区,这就使飞行员可以对此类战斗机进行有效操纵,而这对没有涡流的常规战机来说是很难做到的。另外,强涡流也使战斗机具有异常优异的横侧向稳定性,在越来越具威胁性的现代空战中,明显增强了战斗机的战场生存能力[1-5]。
但是,大后掠三角翼卷起的涡流增加了战斗机绕流流场的复杂程度,给战斗机的气动性能和结构安全性带来了很多负面影响。在大迎角下,连续的涡流结构会破裂形成高度紊乱的尾流,尾流撞击在垂尾上,造成严重的垂尾抖振现象,因此,涡流结构决定了垂尾抖振的强度[4-6]。现代高性能战斗机,如F-16[2],F/A-18[7-12],F-22[13],F-35,由于连续的前缘主涡结构的提前破裂,都受到不同程度的垂尾抖振的困扰,对于具有双垂尾的战斗机,抖振问题更为突出。垂尾抖振现象发生时,加载在垂尾结构上的极限非定常载荷导致垂尾结构的提前疲劳破坏,加剧了战斗机的维护成本,严重缩短了战斗机的综合使用寿命[2-5]。澳洲皇家空军服役的F/A-18就曾因为涡破裂而导致尾翼抖振,急剧缩短了尾翼结构的使用寿命。为此,美国、加拿大、新西兰以及澳大利亚的科研人员组成了一个合作研究团队,致力于解决该型飞机的垂尾抖振问题[11]。
对于双垂尾抖振以及抖振载荷的抑制问题,世界范围内的研究人员已经利用风洞实验、数值模拟以及理论分析等方法进行了大量的基础研究和工程应用研究,研究的重点集中在破裂旋涡流的流动形态以及旋涡破裂的流动控制[2-4]。在此基础上,一些垂尾抖振的抑制方法被提出来[14-16],大致包括被动控制和主动控制两个方面。被动控制[14-15,17-20]不需要外部输入能量,其主要思路是当地外形修正或者增加气动装置,包括加装Gurney襟翼,扰流片,导流栅以及采用新型能量吸收材料等方法。以上的被动控制方法均能有效延迟旋涡破裂,但被动控制往往需要付出额外的代价,例如,浸润面积增大致使阻力增加,新型材料的研制进展缓慢,控制律的通用性及可靠性不足等。因此,人们又研究了主动控制手段对前缘涡破裂的控制作用。主动控制方法[2,14-16]大多需要外部输入能量,其主要思路是连续或周期性吹气/吸气,包括切向吹气,沿着涡轴吹气,后缘吹气/吸气,偏转矢量吹气等方法。主动控制方法具有操作简单,针对性强等优点,但是其控制装置以及控制律设计较复杂、附加成本较高,并且不同飞行状态下的控制效果强烈依赖于吹/吸气位置,因此难以大量推广使用。总之,两种控制方法都没能够在涡结构或破裂点位置的控制上表现出效率或效果上的明显优势,它们都只是根据期望的结果给出了一种独特的控制涡破裂点的可能,要想将这些控制方法可靠而有效地应用于真实飞行中,还需要深刻理解涡流的物理规律,提高预测能力[3]。
华盛顿大学的博士生S. Srigrarom等人提出一种自诱导理论来解释涡破裂现象,该理论指出,在涡破裂的形成过程中,直线涡核周围的剪切层的相互自诱导造成了涡量的卷起,从而诱使出回流以及流面的径向扩张。如果采取一定的方法强迫涡核轨迹由直线变为曲线,那么前缘涡的破裂就会被抑制,垂尾的抖振情况就会有所改善[18-20]。由此,本文中提出一种简单而又可靠的方法以更好地抑制垂尾抖振载荷,从而降低此类战机的维护费用,延长全机的寿命周期。既然垂尾抖振根源于高度紊乱的涡破裂尾流,并且涡流决定垂尾抖振的强度,设想利用机头处的静态的或振动式的鼓包来改变涡流,强迫前缘涡偏离原来的近似直线的轨迹,从而避免与尾翼翼面的直接碰撞,以减轻尾翼翼面周围流动的湍流度,从而抑制尾翼的抖振。为了验证机头静态或振动式鼓包对垂尾抖振抑制的有效性,在西北工业大学的低速风洞内进行了相关验证实验,用垂尾根部应变的均方根值以及频谱分析得到的功率谱密度来定量描述垂尾的抖振响应[5,8,11-12]。
1 实验设备及实验模型
1.1 实验模型
图1是机头左右两侧各有一个鼓包的模型的三视图。原始模型是一个由一个大后掠三角翼和两个垂尾构成的铝制全模,该模型全长为830mm,三角翼的前缘后掠角为70°,根弦长为400mm,厚度为5mm,前缘的下表面有60°的倒角。两侧垂尾的几何外形完全相同,并且对称地安装在模型的尾部,两个垂尾的中性面之间夹角为40°。垂尾的平面形状为直角梯形,根弦长为126mm,展长为130mm,厚度为3mm,尾翼的前缘后掠角为31°,尾翼前后缘两侧的对称倒角均为45°。由图1可以清晰地看到机头左右两侧各有一个圆球形鼓包,两侧鼓包安装位置对称,左侧鼓包的球心位于(0.0894m,-0.0326m,0)处,鼓包半径为7mm,由内部支架紧固。鼓包可以在机体内部电机的带动下分别做上下往复振动(侧视图),振幅为3mm,运动的频率随电机驱动电压的不同而变化,实验中鼓包振动频率与驱动电压的关系详见表1。当驱动电压为2.0V时,鼓包振动的频率为3.55Hz,当驱动电压为6.0V时,鼓包振动的频率为10.65Hz,当驱动电压为12.0V时,鼓包振动的频率为21.30Hz。
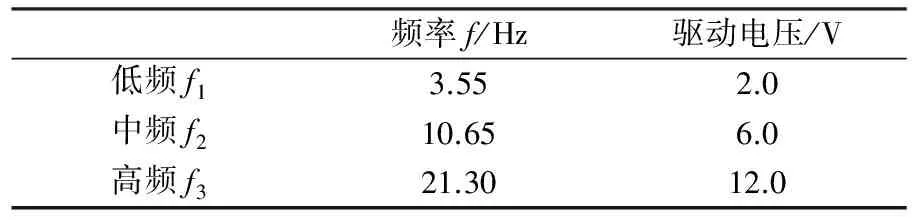
表1 鼓包振动频率与驱动电压的关系

图1 实验模型的三视图
1.2 实验设备和实验条件
验证实验在位于西北工业大学的低湍流度风洞实验室内进行,该风洞是一个开环、低速、低湍流度风洞,其实验段宽度为1200mm,高度为1050mm,长度为2800mm,可提供的风速范围为5~20m/s。实验时对本文模型的测量迎角范围为20°~50°,每2°迎角测量一次,迎角最大时整个模型对风洞的最大壅塞度不超过7.8%。
本实验用垂尾内外两侧半桥连接的应变片测量出的应变来定量表示垂尾的抖振响应,应变片的粘贴位置如图2所示。每个垂尾的内外两侧均粘贴有应变片,两侧的应变片采用半桥方式连接,外侧与内侧应变的差值可以用来表示垂尾抖振响应的大小。在不同的实验条件下,每隔0.00125s用与应变片连接的数据采集系统记录下各个应变片的应变值,采样时间为10.24s,每个实验条件下共有8192组数据。本文的应变为变形值与尾翼厚度的比值,因此应变是无量纲的。

图2 垂尾及应变片位置
1.3 本文的研究目标
为了验证机头前缘处的静态或振动式鼓包对垂尾抖振的减缓效果,在西北工业大学低湍流度风洞实验室进行了相关实验。首先,在风速为10m/s和20m/s的条件下分别对原始模型进行实验,实验的迎角范围为20°~50°,每2°迎角记录一次数据。然后分别对机头左侧装有静态鼓包的模型以及机头左右各装有一个静态鼓包的模型进行实验。最后,对做不同频率振动的左侧鼓包模型进行实验。此时开启机体内部的电机,在电机的驱动下,两侧的鼓包做往复运动,运动的频率随驱动电压的不同而变化。带鼓包模型的实验风速和测量迎角范围与原始模型相同,数据采样频率也完全相同。
2 实验结果及分析
从上述实验中,在每个测试条件下,可以得到10.24s内的垂尾根部内外侧的应变值,采样频率为800Hz,然后可以得到时域内8192组垂尾根部外侧与内侧的应变差值,以这个差值描述抖振响应的大小。在以下的分析中,首先求得抖振响应的均方根值(RMS, Root Mean Square),而均方根说明了垂尾在测试条件下根部变形的波动程度,以RMS作为时域内抖振响应的主要依据。然后用傅里叶变换将时域信号转化到频域,可以得到各个不同实验状态下的主频和功率谱密度(PSD, Power Spectral Density)的峰值,此峰值可以作为频域内的抖振强度的表征。
图3是原始模型左侧垂尾根部应变均方根值随迎角的变化曲线。由该图可以看出,风速为10m/s时,RMS值在整个测量迎角范围内都很小,说明在此风速条件下,垂尾的抖振效应很微弱。风速为20m/s时,RMS值在小迎角时增长缓慢,迎角超过30°时开始急剧增加,在38°时达到最大值,随后减小,从42°开始又继续增加,在46°达到第二个峰值,随后减小。38°和46°对应垂尾抖振最严重的两个状态。下图是风速为20m/s时,左右两侧垂尾翼根应变RMS值随迎角变化曲线的对比图,两条曲线基本重合,说明左右两侧的流动在实验条件下基本对称,左右垂尾的抖振响应相同。


图3 原始模型垂尾根部应变均方根值随迎角的变化曲线
图4是原始模型与静态鼓包模型的翼根应变RMS随迎角的变化曲线,上图对应左侧垂尾,下图对应右侧垂尾。从上图中可以看出,几组模型的左侧垂尾翼根应变RMS变化趋势类似,但是,有静态鼓包的模型RMS值要小于原始模型,并且双侧鼓包模型比左侧鼓包模型稍小。说明机头处鼓包可以有效减缓左侧垂尾的抖振,在38°迎角时,左侧鼓包模型左侧垂尾的翼根弯矩RMS比原始模型减小12.67%,而双侧鼓包模型比原始模型减小15.38%;在46°迎角时,有鼓包的两模型左侧垂尾的翼根弯矩RMS分别比原始模型减小为5.16%,7.04%。
下图中原始模型与左侧静态鼓包模型的右侧垂尾翼根应变RMS随迎角的变化曲线基本重合,说明左侧静态鼓包对右侧垂尾的抖振情况影响不大,有双侧鼓包的右侧垂尾翼根应变RMS小于原始模型对应的值,在38°和46°迎角时,比原始模型分别减小12.67%和7.98%。对比可知,双侧的鼓包对右侧垂尾抖振的减缓效果比左侧稍小。
图5是原始模型与左侧振动式鼓包模型左侧翼根应变RMS随迎角的变化曲线。由图可知,在迎角为30°以下时,3组振动式鼓包模型对应的值比原始模型有所减小,但是减小幅度非常小。迎角继续增大,低频振动模型的值明显小于原始模型,而另外两组模型相对于原始模型的减小量仍然不太明显。在38°迎角时,低频、中频、高频3组模型左侧垂尾的翼根弯矩RMS分别相对原始模型的改变量分别为-23.98%,0.45%,-4.98%;而在46°迎角时,低频、中频、高频3组模型左侧垂尾的翼根弯矩RMS分别相对原始模型的改变量分别为-12.21%,-4.69%,-5.63%。由此得出结论,对本文所用模型来说,低频振动鼓包比中频和高频鼓包更加有效地抑制了垂尾的抖振。


图4 原始模型与静态鼓包模型翼根应变RMS随迎角变化曲线
Fig.4 RMS of tail root strain for the original model and models with static bulges

图5 原始模型与左侧振动式鼓包模型翼根应变RMS随迎角变化曲线
Fig.5 RMS of tail root strain for the original model and models with left vibrating bulges
图6是分别是在迎角为38°时对不同模型的左侧翼根应变进行傅里叶变换后的频谱图。由图可知,虽然不同模型的功率谱密度峰值有所差别,但是主频都大致相同,保持为52Hz。
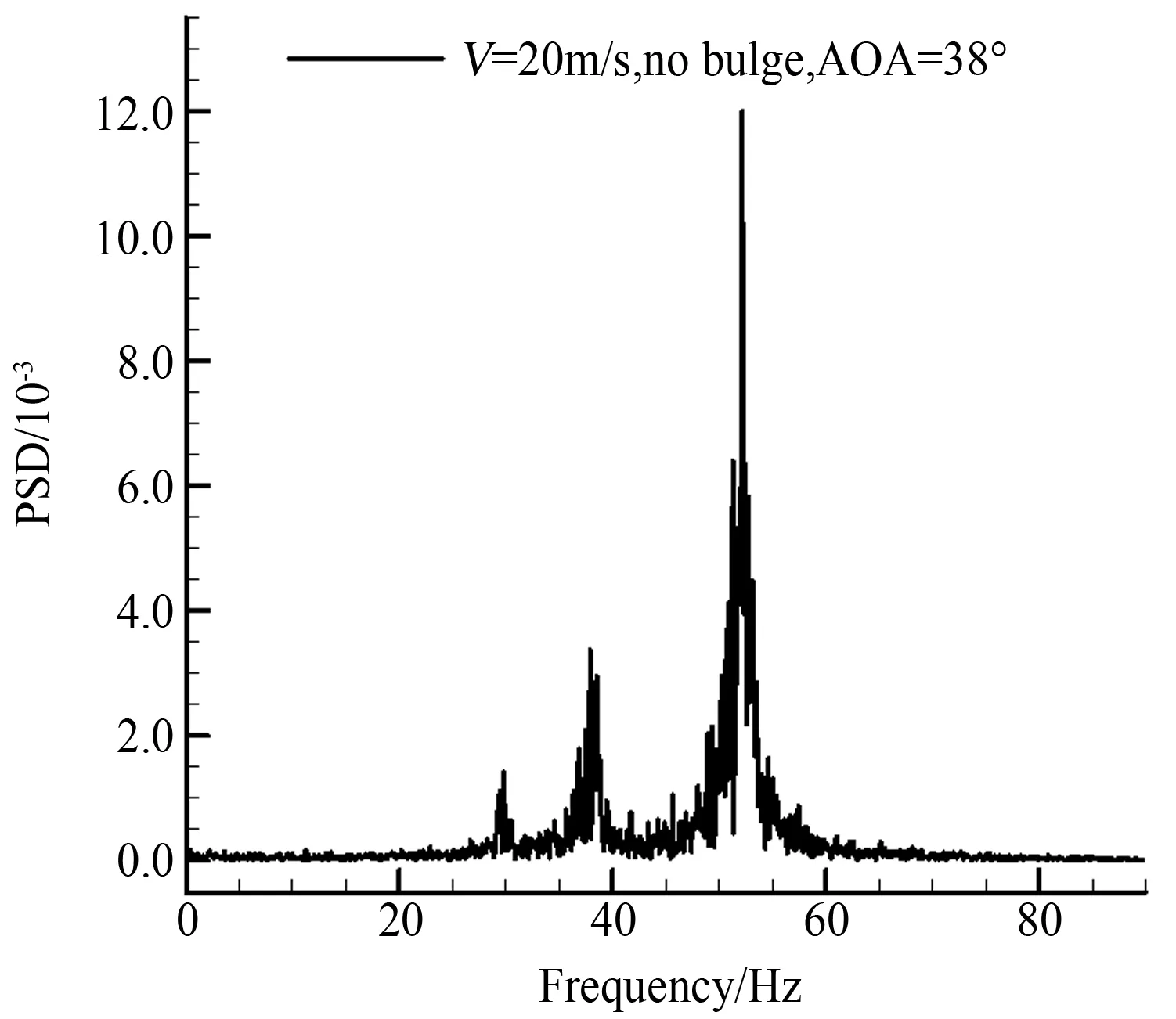


图6 迎角为38°时不同模型的频谱图
图7是原始模型与两组有静态鼓包模型的左侧垂尾翼根应变的功率谱密度峰值随迎角的变化曲线,功率谱密度峰值对应抖振最严重的状态,是抖振响应程度的重要标志。由图可知,3组曲线变化趋势类似,在迎角小于30°时,功率谱密度的峰值随着迎角的增大缓慢增加,当迎角超过30°时,开始剧烈增加,在38°时达到最大值,随后减小,接着又开始增加,在46°时达到第2个峰值,然后开始降低。比较而言,有机头鼓包的两组模型的值比原始模型小,但是在小迎角时减小幅度不大,迎角超过36°时才有明显减小。在迎角为38°时,左侧鼓包模型和双侧鼓包模型分别比原始模型减小38.17%,40.50%;迎角为46°时,左侧鼓包模型和双侧鼓包模型分别比原始模型减小21.44%,22.68%。
图8是是原始模型与左侧振动式鼓包模型的左侧垂尾翼根应变的功率谱密度峰值随迎角的变化曲线。由图可知,以不同频率振动的鼓包对左侧垂尾翼根应变的影响情况各不相同。在小迎角时,图中4组模型对应的值没有显著差别,在大迎角时,差别较为明显。在迎角为38°时,低频、中频、高频3组模型对应的值分别比原始模型减小48.92%,40.50%,32.83%。在迎角为46°时,低频、中频模型对应的值分别比原始模型减小14.11%,16.04%,而高频模型对应的值比原始模型增加16.60%。再对比图7的结果可知,对本模型来说,以低频振动的机头鼓包对垂尾抖振的减缓作用最为显著,在38°和46°两个垂尾抖振最严重的状态,有效降低了垂尾翼根应变功率谱密度的峰值。

图7 原始模型与静态鼓包模型功率谱密度峰值对比图
Fig.7 Comparison of peak of PSD between the original model and models with static bulges

图8 原始模型与左侧振动式鼓包模型功率谱密度峰值对比图
Fig.8 Comparison of peak of PSD between the original model and models with left vibrating bulges
3 总结与展望
三角翼双垂尾布局飞机在进行大迎角飞行时,前缘涡不可避免地会在垂尾之前破裂,涡破裂尾迹形成高度不规则气动载荷激励,直接撞击在垂尾上引起垂尾结构的强迫振动,造成垂尾结构的疲劳甚至破坏,这就是三角翼/双垂尾布局战斗机的垂尾抖振现象。本文根据自诱导理论提出了一种新方法,用机头处静态或振动式鼓包来改变涡流的发展规律,延缓涡流的破裂,从而抑制抖振,并且在风洞内进行了相关验证实验。本实验用垂尾根部的应变值及其对应的功率谱密度来定量描述垂尾的抖振响应,可以得到以下结论:
(1) 在一定的来流条件下,静态的或是振动式的鼓包都能有效抑制垂尾抖振。振动式鼓包的抖振抑制效果与振动频率有关,在大迎角下(大于36°),低频振动鼓包的抑制效果更好。
(2) 某一侧的鼓包仅能影响该侧涡流,从而减缓该侧垂尾抖振强度,它对另一侧垂尾抖振没有明显影响。
(3) 本文中所用鼓包在实验条件下都有一定程度的抖振抑制效果,同时并没有改变垂尾振动的主频,该值保持在52Hz。
风洞实验结果证明了本文中所用鼓包在实验条件下的抖振抑制效果,虽然本文关注的重点是大后掠三角翼/双垂尾布局的双垂尾抖振抑制,但这种抖振抑制的思路可以推广到其它布局的飞行器上。下一步工作重点包括用多种流场显示方法揭示前缘涡的演化过程,鼓包将涡流由直线改变为曲线的具体过程,以及抖振响应与鼓包振动频率的具体关系。深入理解这些问题是将该方法可靠而有效地进行工程应用的前提。
[1] Menke M, Yang H, Gursul I. Experiments on the unsteady nature of vortex breakdown over delta wings[J]. Experiments in Fluids, 1999,27(3):262-272.
[2] Lee B H K. Vertical tail buffeting of fighter aircraft[J]. Progress in Aerospace Sciences, 2000, 36(3): 193-279.
[3] Mitchell A M, Délery J. Research into vortex breakdown con- trol[J]. Progress in Aerospace Sciences, 2001, 37(4): 385-418.
[4] Lucca-Negro O, O’doherty T. Vortex breakdown: a review[J]. Progress in Energy and Combustion Science, 2001, 27(4): 431-481.
[5] Breitsamter C. Unsteady flow phenomena associated with leading-edge vortices[J]. Progress in Aerospace Sciences, 2008, 44(1): 48-65.
[6] Lee B H K. Statistical analysis of wing/fin buffeting response[J]. Progress Journal of Aircraft, 2005, 42(2): 299-319.
[8] Lambert C, Gursul I. Characteristics of fin buffeting over delta wings[J]. Journal of Fluids and Structures, 2004, 19(3): 307-319.[9] Younjong Kim, Ozgoren M, Rockwell D. Vortex breakdown-tail interaction[J]. AIAA Journal, 2003, 41(3): 544-549.
[10] Bean D E, Wood N J. Experimental investigation of twin-fin buffeting and suppression[J]. Journal of Aircraft, 1996, 33(4): 761-767.
[11] Hangan H, Vickery B J. Buffeting of two-dimensional bluff bodies[J]. J Wind Engineering and Industrial Aerodynamics, 1999, 82(1): 173-187.
[12] Vlahostergios Z, Missirlis D, Yakinthos K, et al. Computational modeling of vortex breakdown control on a delta wing[J]. International Journal of Heat and Fluid Flow, 2013, 39: 64-77.
[13] Caroline Lambert, Ismet Gursul. Insensitivity of unsteady vortex interactions to Reynolds number[J]. AIAA J, 2000, 38(5): 937-939.
[14] Gursul I, Vardaki E, Wang Z. Active and passive control of reattachment on various low-sweep wings[R]. AIAA Paper, 2006, 506: 2006.
[15] Stanewsky E. Adaptive wing and flow control technology[J]. Progress in Aerospace Sciences, 2001, 37(7): 583-667.
[16] Caruana D, Mignosi A, Corrège M, et al. Buffet and buffeting control in transonic flow[J]. Aerospace Science and Technology, 2005, 9(7): 605-616.
[17] Lowson M V, Riley A J. Vortex breakdown control by delta wing geometry[J]. Journal of Aircraft, 1995, 32(4): 832-838.
[18] Srigrarom S, Lewpiriyawong N. Controlled vortex breakdown on modified delta wings[J]. Journal of Visualization, 2007, 10(3): 299-307.
[19] Srigrarom S, Kurosaka M. Shaping of delta-wing planform to suppress vortex breakdown[J]. AIAA Journal, 2000, 38(1): 183-186.
[20] Srigrarom S, Kurosaka M. Surface shaping to suppress vortex breakdown on delta wings[J]. AIAA Journal, 2000, 38(1): 186-187.
(编辑:张巧芸)
Experimental study on a novel method for vertical tail buffet suppression
Zhang Qing, Hua Ruhao, Ye Zhengyin
(National Key Laboratory of Aerodynamic Design and Research, Northwestern Polytechnical University, Xi'an 710072, China)
The twin tails of the modern high performance fighter aircrafts with delta wing/twin vertical tails configuration generally experience significant dynamic load due to aerodynamic buffet caused by highly unsteady vortex breakdown flow. This paper proposes a new type of buffet alleviation method by solid static or oscillating bulges attached on the forebody of a delta wing model, and conducts wind tunnel experiment for the model which consists of a sharp-edged, 70-degree leading edge sweep delta wing, and twin 31° leading edge sweep vertical tails. The model has been tested at 10m/s and 20m/s of free stream velocity, and at angle of attack ranging from 20° to 50° with an interval of 2° in the low-speed wind tunnel at Northwestern Polytechnical University. According to the self-induced theory proposed by experts from University of Washington, the bulges attached on the forebody of a delta wing would twist and kink the vortex core, change the vortex trajectory after the bulge, delay the vortex breakdown position, and decrease the fluctuating level of the flow around the twin vertical tails. Thus the goal of buffeting suppression is achieved. This study aims at investigating the buffet alleviation effect of the static or vibrating bulges attached on the forebody surface of the model. Two pairs of half bridged strain gauges are employed for the measurement of unsteady root strain on the vertical tails, with one pair on each side. The experimental results show that both static and vibrating bulges behave positively as a novel tool to alleviate tail buffet, and the alleviation effect correlates with the vibrating frequency. Besides, the bulge on one side can only alleviate the buffeting for the tail of the same side, and it has no obvious alleviation effect for the tail on the opposite side. Results of spectral analysis prove that the bulges used in this experiment could alleviate tail buffeting, but they do not change the dominant frequency of the oscillation of the tails in the vortex breakdown flow.
forebody bulge;high sweep delta wing;leading edge vortex;self-induction theory;buffet suppression
1672-9897(2015)01-0037-07
10.11729/syltlx20140020
2014-03-04;
2014-06-23
国家自然科学基金(11072199)
ZhangQ,HuaRH,YeZY.Experimentalstudyonanovelmethodforverticaltailbuffetsuppression.JournalofExperimentsinFluidMechanics, 2015, 29(1): 37-42. 张 庆, 华如豪, 叶正寅. 一种新型垂尾抖振抑制方法实验研究. 实验流体力学, 2015, 29(1): 37-42.
V211.4
A

张 庆(1988-),男,湖北襄樊人,博士研究生。研究方向:大后掠三角翼垂尾抖振抑制。通信地址:陕西省西安市友谊西路127号西北工业大学航空学院翼型叶栅空气动力学国防科技重点实验室中楼203室(710072)。E-mail:zhangqing2220@mail.nwpu.edu.cn
