威布尔比例风险模型装备状态维修检测间隔期研究

张仕新，昝 翔，李 浩，韩朝帅

（装甲兵工程学院，北京 100072）

威布尔比例风险模型装备状态维修检测间隔期研究

张仕新，昝 翔，李 浩，韩朝帅

（装甲兵工程学院，北京 100072）

针对装备的实际寿命受到多种复杂因素影响的情况，以威布尔比例风险模型为基础，建立了反应装备状态的可靠度模型，针对传统参数估计方法的不足，提出了利用遗传算法进行模型参数估计的方法。同时，利用主成分分析法，保证原始数据信息损失最小的情况下,以少数的综合变量取代原有的多维变量,简化了状态参数。以故障风险为决策目标，建立了状态维修检测间隔期决策模型。通过实例，验证了该方法的可行性和有效性。

威布尔比例风险模型，状态维修检测间隔期，遗传算法，主成分分析

0 引言

随着高新技术的应用，装备的故障规律和故障模式日趋复杂化，定时维修的适用范围逐步减小，使得状态维修［1］（Condition-based Maintenance，CBM）逐步得到重视和推广，在保证可靠性的前提下提高装备的可用度。对于装甲装备实现精确保障，减少维修保障费用具有重要的意义。

维修决策时CBM的关键步骤之一，目前可以用于状态维修决策的模型有很多，比例风险模型（Proportional Hazards Model，PHM）就是重要的模型之一。能够将状态参数引入可靠度模型中，综合考虑装备役龄与状态参数的变化，为维修决策提供有力支持。李小波［2］等通过建立比例风险模型预测装备的剩余寿命，并以发动机的某类轴承为例，进行了维修决策研究。满强［3］等利用比例风险模型建立了状态信息的故障率模型，实现了状态维修决策。

目前，大多的CBM检测间隔期模型以维修费用为目标，无法很好地满足可靠性和安全性的目标，并且多数的间隔期决策模型建立在等间隔期的基础上，忽视了装备状态的劣化特点。因此，本文以控制故障风险为目标，建立CBM检测间隔期动态决策模型，根据状态变化，及时调整检测间隔期，降低装备的故障风险概率。

1 威布尔比例风险模型的建立

PHM模型是Cox［4］于1972年率先提出的。PHM模型将状态参数、工作载荷，故障等因素视为装备寿命的伴随影响因素，并将这些因素视为失效风险函数的协变量，并且对装备的实际风险产生乘积效应［5］。

1.1 威布尔比例风险模型

比例风险模型［6］具有如下性质：不同个体的风险成比例。比例风险模型形式为：

由于威布尔分布能够较好地拟合大部分机电类产品的寿命分析规律，因此，采用到威布尔比例风险模型（Weibull Proportional Hazards Model,WPHM）建立装备的可靠度模型。

结合比例故障模型和两参数威布尔分布，可以得到WPHM的分布形式，可以利用该模型描述状态与故障率的关系。其表达式为

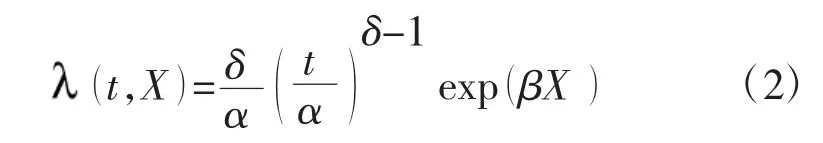
其中，t0为尺度参数，α为尺度参数，Z是p维协变量，X装备的状态信息；β是协变量的系数向量，并且。

1.2 基于遗传算法WPHM模型参数估计

传统方法是通常使用Newton-Raphson迭代算法进行参数估计，但是该方法极易形成局部最优解，且受到估计初值的影响较大，得到的结果往往不够准确。遗传算法具有较强的全局寻优能力，并且不受估计初值的影响。因此，本文选择遗传算法进行参数估计。

在工程应用中，可以利用Matlab中的遗传算法工具箱GOAT［7］进行遗传算法的计算。基于遗传算法的威布尔比例风险模型的参数估计步骤为：

1.2.1 确定编码方式

染色体的编码方式通常采用十进制或者二进制。在选定了编码方式以后，就可以进一步确定各待估参数在染色体内的长度和位置。

1.2.2 设置计算参数

需要设置的参数包括种群的规模，染色体的选择方式、交叉方式、交叉率、变异方式、变异率等等。

1.2.3 确定适应度函数

装备状态的联合概率密度似然函数为：

式中：R（Tj）表示第i台的可靠度函数表示第i台装备的故障密度函数；p（Xj-1i，Xji）表示由Xj-1i转变为Xji的概率。

根据式（3），可得含有状态参数的装备可靠度函数为：

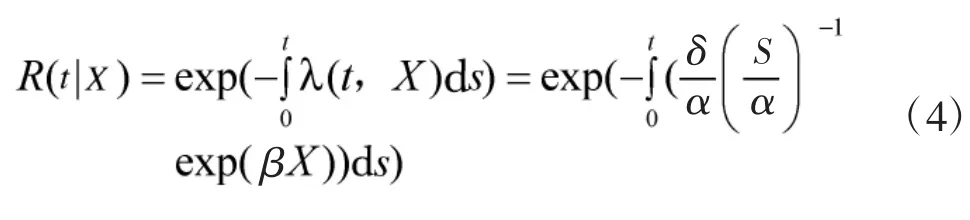
将式（3）和式（7）代入式（8），可得

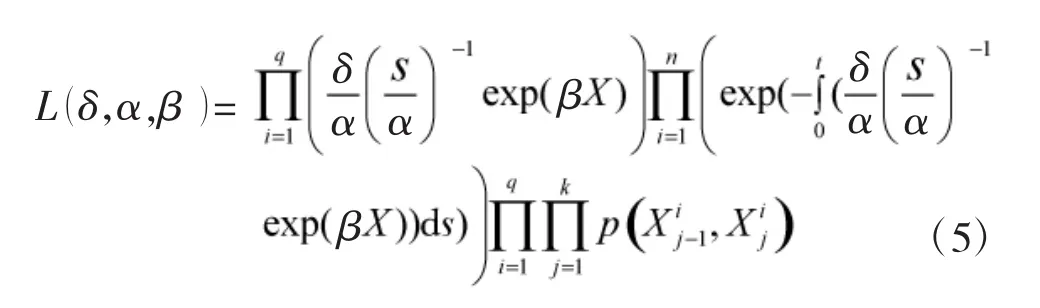
两边取对数，可得

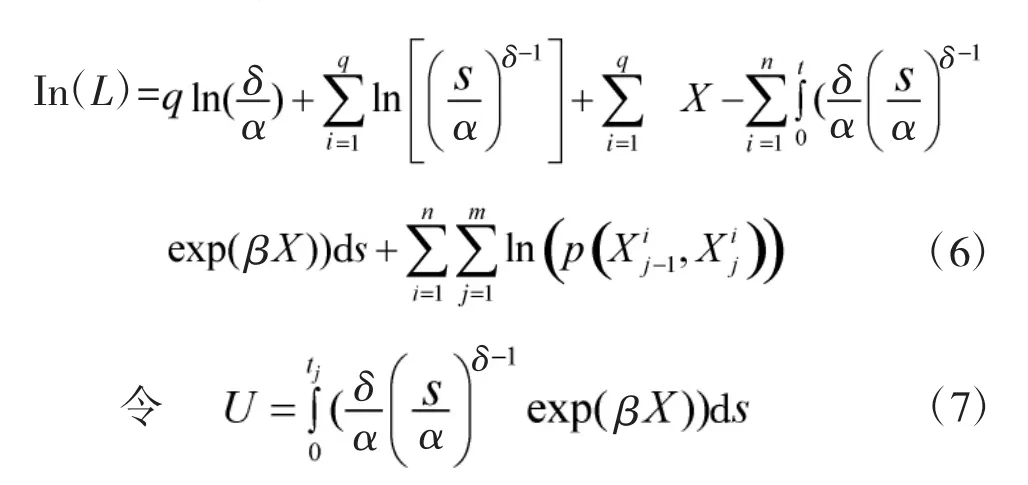
由于假设装备的状态变化规律为右阶跃函数，所以式（11）可以表示为：

可得，遗传算法的适应度函数为：

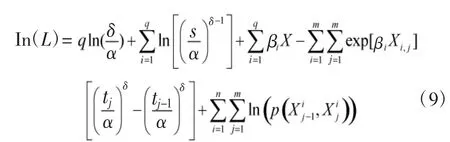
1.2.4 迭代运算

根据威布尔分布参数的意义，结合工程实践经验，可以确定各待估参数的取值范围为：

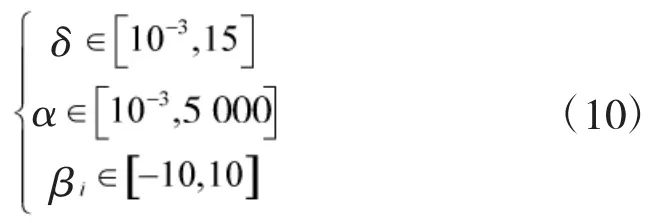
利用多步的迭代运算直到满足终止条件，输出最优解。

通过以上遗传算法的步骤，利用Matlab软件可最终求得可以求出α、δ和βi的估值。

1.3 状态参数确定

在WPHM模型中，通过观测值求得表征状态值Xi是关键步骤之一。在原始数据中，状态参数往往不是唯一的，当参数的维数较高时会导致计算量偏大，同时也容易产生较大的误差，需要通过降维处理来减小这些误差。

提取状态参数的步骤如下：

1.3.1 数据预处理

由于操作不当，会导致部分检测数据出现明显的误差，这些误差会干扰对状态的判断，所以在进行维修决策前必须将明显偏离正常值的数据剔除。

1.3.2 数据归一化

由于可能有不同种类的数据表征同一维修单元的状态，这些数据的量纲不同，属性值的数量级也可能存在差异。所以，在进行主成分分析之前，需要对数据进行归一化处理。

1.3.3 主成分分析

①对样本数据进行预处理和归一化后，计算处理结果的协方差矩阵

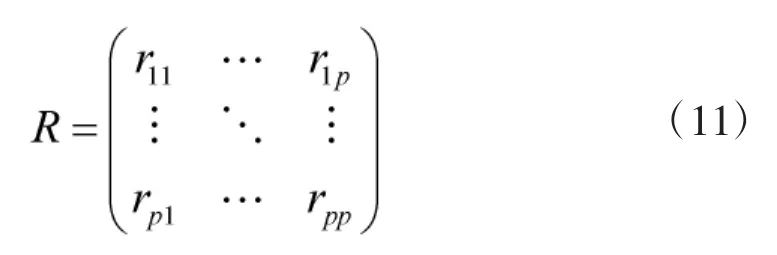
式中：rij为xi和xj的相关系数。

③通过计算前m个主成分的累积贡献率

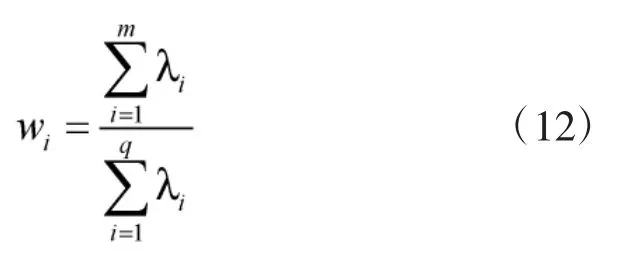
当累积贡献率超过80%时，可以认为前m个主成分几乎包含样本数据的所有特征。

1.3.4 计算状态参数

将所求的m个主成分与各个状态参数乘积的线性组合结果，作为最终的状态参数。

2 基于故障风险的检测间隔期决策

2.1 故障风险的概念

装备的故障风险［9］是指在工作到t时刻检查时确认状态完好的前提下，下一检测间隔期△t内发生故障的概率。若装备的寿命为T，装备故障风险为r，则有以下表达式：

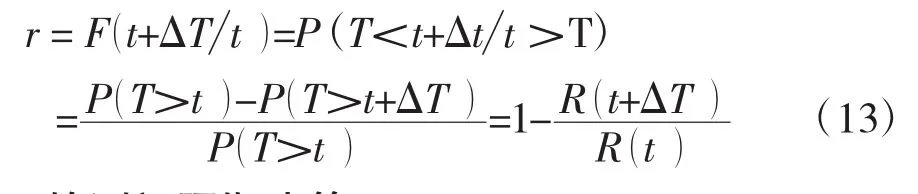
2.2 检测间隔期决策

基于故障风险的状态维修检测间隔期决策的目标，是通过控制故障风险得出最优检测间隔期。通常是设定某一故障风险阈值或者一个故障风险的接受范围，随时对装备的运行和状态参数的更新对条件失效概率分布进行分析，从而对检测间隔期进行动态据决策。

将式（2）代入式（13）可得：

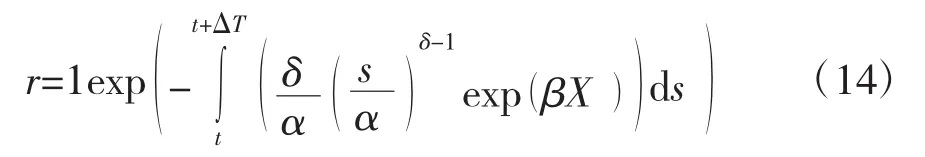
假设装备的状态变化规律为右阶跃函数，即只在检测点发生突变。将估计值代入式（4）。则式（4）可以简化为：

由式（5）可以得出检测间隔期的计算式为：

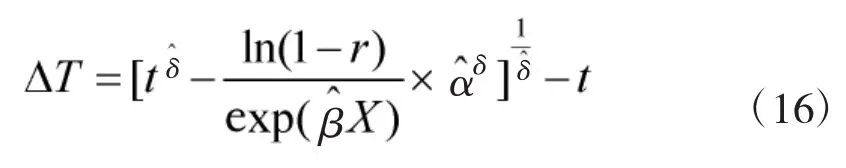
3 实例分析

3.1 实例背景

选取某装备发动机的油液检测数据进行分析，选取主要金属磨损检测数据为样本数据。样本为两辆同样型号车辆，在同种工作条件下运行，定时对发动机油液数据进行检测数据，将2号车检测数据作为样本数据进行参数估计，1号车数据作为验证数据。2号车数据处理后的结果如下页表1所示。

3.2 状态参数确定

按照式（11）、式（12）进行主成分分析。结果，第1主成分的贡献率达到了92.43%，因此，可以将认为第1主成分几乎包括了样本的全部信息。通过计算可得第一主成分的系数为：a=［0.4,51,0.453，0.455,0.419，0.456］。

最终，可以求得状态参数，如下页表2所示。

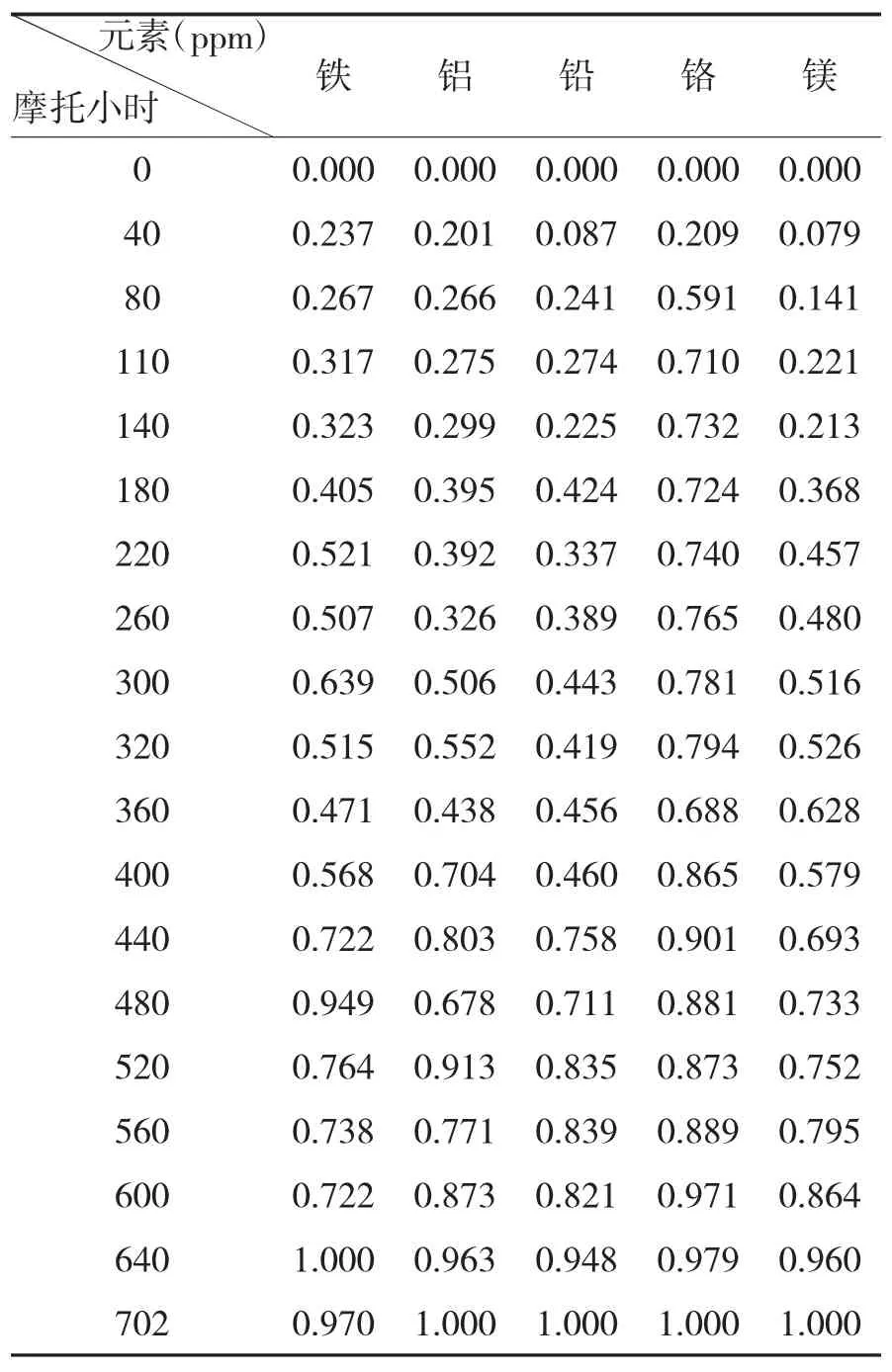
表1 2号车检测数据归一化处理结果

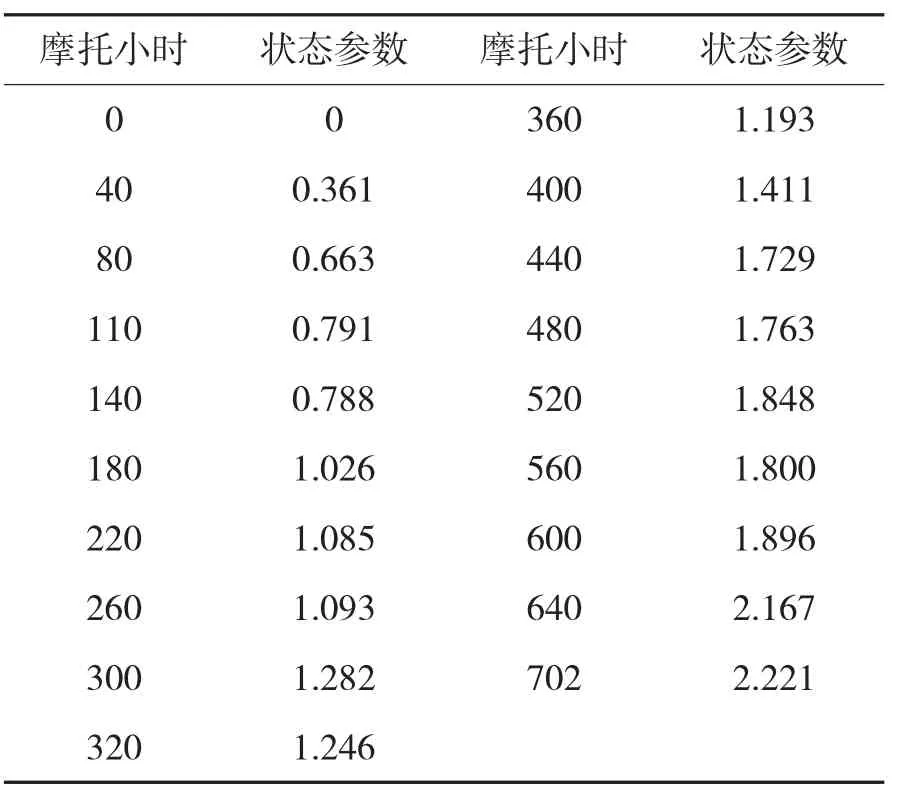
表2 2号车检状态参数

3.3WPHM模型参数估计

利用遗传算法，利用表2中的状态参数对WPHM模型中的参数进行估计，所得的计算结果为：

即所求得的WPHM模型为

3.4 检测间隔期计算

3.4.1 数据处理

取1号车数据，经过预处理、归一化、主成分分析等步骤后，最终求得的状态参数如表3所示。

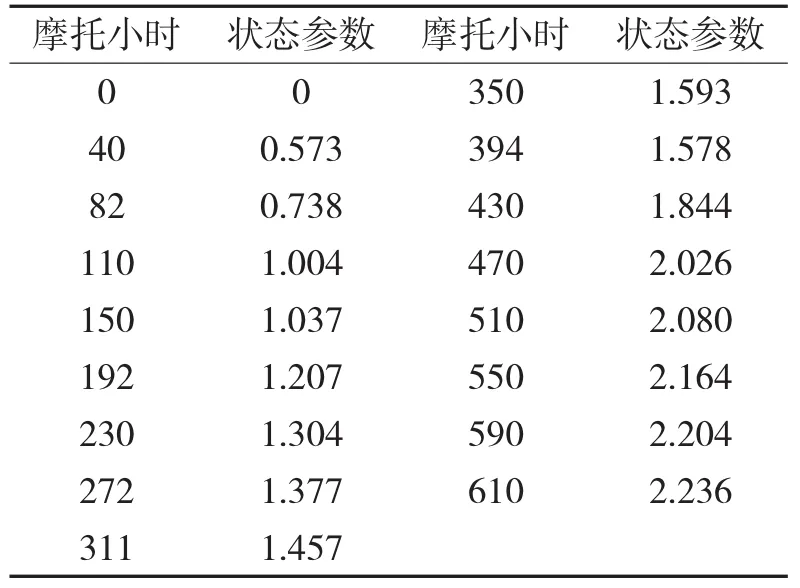
表3 1号车状态参数

3.4.2 算式确定

根据以上计算结果，可得检测间隔期的计算式为：

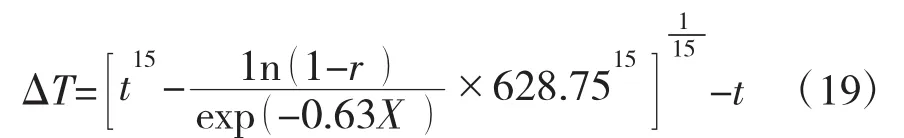
由于故障风险过大，会导致装备运行的危险程度加大；故障风险过小，会导致维修费用的大幅度增加。根据经验，装备故障风险在r∈［0.02,0.05］范围内均可以接受。

3.4.3 最终结果计算

根据技术状态评估结果进行维修决策，1号车发动机在430摩托小时以后需要减小检测间隔期。所以，可以给出1号发动机的最优检测检测期的决策结果，如表4所示。

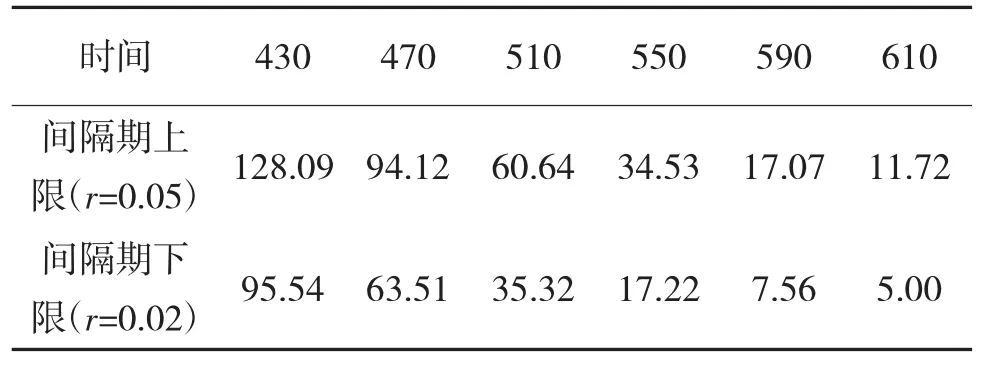
表4 1号车状态参数

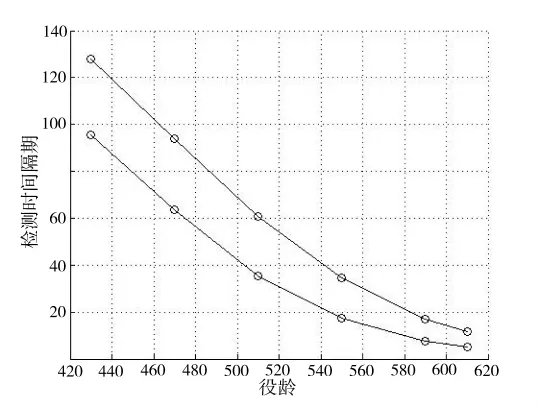
图1 检测间隔期调整决策范围

根据表4的决策结果，绘制如图1所示的检测间隔期调整决策图，可行的检测期范围内，根据实际情况，综合考虑，最终得到最优检测间隔期。

4 结束语

本文将由装备状态检测信息作为观测值求得的状态参数作为协变量，引入了装备可靠度模型中，并且通过威布尔比例风险模型将二者有机的结合。以控制故障风险为决策目标，以检测间隔期为决策变量，进行了状态维修检测间隔期决策。通过给出故障风险范围，为决策者提供了充分的决策空间。

［1］马飒飒，贾希胜，夏良华.军队装备维修工程CBM综述［J］.装备指挥技术学院学，2008，19（2）：111-116.

［2］李小波，王宏伟，李良锋，等.基于PHM的发动机旋转部件状态维修决策研究［J］.科学与技术工程，2011，36（11）：9113-9115.

［3］满强，陈丽，夏良华，等.基于比例风险模型的状态维修决策研究［J］.装备指挥技术学院学报，2008，19（6）：36-39.

［4］Lawless J F.寿命数据中的统计模型与方法［M］.北京：中国统计出版社,1998.

［5］Jiang S T,Landers T L,Rhoad T R.Assessment of Repairable-system Reliability Using Proportional Intensity Model：a Review［J］.IEEE Transactions on Reliability, 2006,55（2）：328-336.

［6］左洪福，蔡景.维修决策理论与方法［M］.北京：航空工业出版社，2008.

［7］方元华，胡昌华，李瑛.基于遗传算法的威布尔分布参数估计及MATLAB实现［J］.战术导弹控制技术，2007，56（1）：100-103.

［8］骆行文，姚海林.基于主成分分析的岩石质量综合评价模型与应用［J］.岩土力学，2010，31（增刊2）：452-455.

［9］张耀辉，郭金茂，徐宗昌，等.基于故障风险的状态维修检测间隔期的确定［J］.中国机械工程，2008，19（5）：555-558.

Weibull Proportional Hazards Model Based Determination of the Test Intervals for Condition Based Maintenance

ZHANG Shi-xin，ZAN Xiang，LI Hao，HAN Chao-shuai
（Academy of Armored Force Engineering，Beijing 100072，China）

According to the fact the real life of equipment is from complex factors，based on WeibullProportionalHazardsModel（WPHM）,reliability modelisestablished.Considering disadvantage of traditional methods,genetic algorithm is utilized to estimate the values of model parameters.At same time,A few conditional parameters can substitute for original multidimensional variables by principal component analysis with little data information lost.Based on failure risk,test intervals model for Condition Based Maintenance（CBM）is established.The result shows the model works well and effectively.

WPHM，test interval of CBM，genetic algorithm，principal component analysis

TH17

A

1002-0640（2015）07-0151-04

2014-05-10

2014-07-25

张仕新（1971- ），男，河北青龙人，博士，副教授，硕士生导师。研究方向：装备维修理论与技术方面的研究。