指定目标不延误条件下的拦截决策算法*

高建军，韩金城，刘冠英，郭 强，崔艳丽

（防空兵学院，郑州 450052）

指定目标不延误条件下的拦截决策算法*

高建军，韩金城，刘冠英，郭 强，崔艳丽

（防空兵学院，郑州 450052）

从现有的拦截排序准则出发，根据实际作战中进袭目标的特点，应用现代排序理论，分别建立了动态目标拦截排序模型和总损失最小化模型，给出相应的求解算法。最后实例计算得出模型既体现了现有的拦截准则，又对现有的准则进行了推广。

威胁判断，拦截排序，防空导弹，火力单元

0 引言

对于程序化指挥控制决策而言，一般在信息场搜索发现目标、跟踪目标、计算诸元和目标识别后要进行目标威胁判断，程序化防空导弹射击指挥控制辅助决策，所以必须嵌入目标威胁判断模块，是因为一个国家或地区的防空资源有限，又必须对众多被掩护对象提供掩护，而空袭是动态、多变的，当空袭方集中对某些被掩护对象突击，特别是采用中、大规模空袭编队进袭时，防空导弹火力单元（群）往往面临超饱和的目标数量［1-2］。为此，必须分轻重缓急，先拦截威胁值最大的目标，完成射击循环后，再拦截其他目标。因此，目标拦截次序是否科学、合理，将直接影响着防空作战效能的高低。本文通过建立数学模型，首先研究了动态目标情形，其次探讨在上级指定目标不延误条件下，我防空导弹火力单元拦截目标的先后次序，使总损失最小。

1 拦截排序问题

1.1 拦截排序现状

拦截排序，是防空导弹射击指挥控制中的关键子过程，是指挥控制结构化辅助决策的关键功能模块。随着防空体系的发展，国内外学者对拦截排序已有很多研究，提出了很多的准则和方法，这些准则和方法实际上是按作战效能得出的，就查阅文献看来，当前这些准则［3］主要包括：

（1）对上级指定优先拦截的目标，按上级指定的次序优先拦截。

（2）对火力单元自行判断威胁值大的目标，优先拦截。

（3）对威胁值相同或相近的目标先到先拦截。

（4）当发射区内存在多个威胁值相同或相近的目标时，先拦截近的，后拦截远的。

（5）当发射区内存在多个目标时，先拦截远的，后拦截近的。

对于前三条准则不存在争议，而后两条则是对立的。大多数都认为先拦截近的，后拦截远的。文献［3］详细分析了这两种对立的情况，得出“对于单通道火力单元应先打近后打远；多目标通道火力单元应先打远后打近，但对逼近有效发射区近界的空中目标应先打近后打远”。文献［4］指出合理的拦截次序应该是根据空袭目标的实际情况，以及我防空武器系统的数量，特别要将空袭目标的拦截剩余时间和优化目标等因素综合加以考虑，充分利用拦截纵深，确定合理的拦截次序，使得拦截效能最大。同时文献［4］考虑在面对饱和的空袭目标，我防空导弹火力单元不可能一一拦截时，建立上级指定目标不延误条件下，我防空导弹火力单元拦截决策模型，把“延误的目标数量最少”作为优化目标进行了研究，但这里所采用的算法是静态算法，是通过反复调用静态算法来研究目标的动态情形。本文在文献［4］的基础上首先讨论了动态目标情形，直接应用经过严格论证过的动态算法研究动态目标的拦截决策问题。其次，讨论在上级指定目标不延误条件下，把目标对我造成的总损失作为目标函数加以研究，试图为拦截决策提供合理的依据。

1.2 连续跟进目标的拦截条件

一个目标通道拦截多个目标时，应尽早拦截可以利用空中目标的前后时间间隔和拦截纵深，一个目标通道可通过火力转移向同一编队的多个空中目标进行拦截，从而充分发挥一个火力单元的作战效能。一个目标通道拦截2个连续跟进空中目标的条件［5］：

其中，△LLS2为第2个空中目标到对应发射区近界的距离，即空中目标2的拦截剩余距离；△Lfy1为第1个空中目标对应发射区远界的距离；vm1为第1个空中目标的飞行速度；tmzy1为防空导弹与空中目标1在杀伤区远界的遭遇时间；te为一次连射导弹发射时间间隔总和；tp为对一个空中目标的射击结果评定时间；tz为目标通道从射击一个空中目标转向射击另一个空中目标的火力转移时间；vm2为第2个空中目标的飞行速度。

也可以写时间表达形式：

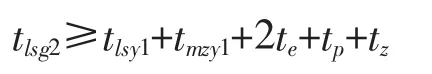
其中，tlsg2为第2个空中目标的拦截剩余时间；tlsy1为第1个空中目标到达其发射区远界的时间。

2 动态拦截模型

2.1 模型假设

（1）待拦截的各目标为同类目标。

（2）一次拦截后，指挥控制系统能继续转火，向未被杀伤的目标实施拦截。

（3）在我防空武器系统充足的条件下，所有目标都是可拦截并能被毁伤的目标。

（4）上级指定的拦截目标在优先拦截条件下不会发生延误。

（5）进袭目标为动态目标。

（6）如果目标进入发射区的时间与最晚拦截时间具有一致性关系。

2.2 模型建立

设作战持续时间内，进袭的目标构成目标集M={M1，M2，…，Mn}，各目标进入发射区的时间分别为r1，r2，…，rn，最晚拦截时间分别为t1，t2，…，tn，进入发射区的时间与最晚拦截时间满足一致性关系，也就是当ri≤rj时，ti≤tj。上级指定优先拦截的目标集T={Mj1，Mj2，…，Mjk}，k≤n，E=M/T={Mi1，Mi2，…，Mil}，k+l=n，设目标Mj（j=1，2，…，n）的拦截剩余时间tlsgj（j=1，2，…，n），并设sj为拦截目标Mj的防空导弹发射时间，pj为导弹拦截目标Mj的实际拦截时间，C{M}表示目标集M的拦截总时间，Uj为未杀伤的目标对我攻击的单位损失，cj为导弹与目标Mj的遭遇时间，满足cj=sj+pj。因目标Mj（j=1，2，…，n）必须在杀伤区内被杀伤，因此，必须在tlsgj-pj之前开始发射导弹，若cj＞tlsgj，则目标未被杀伤，可能投弹对我攻击，因此，发生拦截延误，对我造成损失，记作Uj=1，若cj≤tlsgj，则未发生拦截延误，记作Uj=0，问题是确定一个拦截方案，使得在上级指定目标不延误条件下，尽可能杀伤更多的目标，对我造成的损失∑Ui最小。

2.3 算法

2.3.1 引理

本文考虑单目标通道拦截动态目标决策问题，在进入发射区的时间与最晚拦截时间满足一致性关系条件下，使总损失∑Ui最小化，把这一问题简称为动态一致损失决策问题。

定义：对于目标集M的子集T，如果在子集T的一个拦截排序中，这些目标都没有发生延误，那么这个子集T称为不延误目标子集。

下面利用引理说明“动态一致损失决策问题”有最优解的必要条件和最优解的结构［6-7］。

引理1动态一致损失决策问题有最优解的必要条件是T，是不延误目标子集。

引理2动态一致损失决策问题存在最优解，其拦截次序可以分为前后两部分：①不延误的目标按拦截剩余时间由小到大排序；②延误的目标，以任意次序排在后面。

2.3.2 算法

步骤1：设决策时刻上级指定的目标

T={Mj1，Mj2，…，Mjk}，k≤n，

及需要拦截的其他目标

E=M/T={Mi1，Mi2，…，Mil}，k+l=n。

步骤3：令E0=T，ME0={Mi1，Mi2，…，Mil}。

步骤4：E0=T中的目标按照最短拦截剩余时间tlsgj由小到大的顺序拦截。

步骤5：若k=l+1，算法终止，（El，MEl）就是最优排序；若k＜l+1，转步骤6。

步骤6：按照拦截剩余时间和拦截两个连续跟进目标的条件确定拦截顺序，

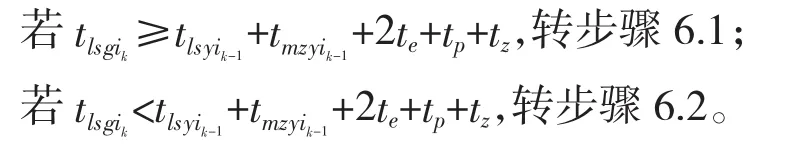
步骤7：令k=k+1，转步骤5，当有新目标出现或原有目标未被毁伤，转步骤1。

2.3.3 算法的最优性

引理由算法2.3.2所产生的拦截目标排序是动态一致损失决策问题的最优解。

3 总损失最小化模型

3.1 模型假设

在2.1模型假设（1）～假设（4）下，另外假设：

（1）目标拦截剩余时间与权重具有一致性关系。

（2）未及时拦截目标对我造成的损失与目标权重成正比。

3.2 拦截排序模型

设作战持续时间内，进袭的目标构成目标集M={M1，M2，…，Mn}，各目标权重分别为w1，w2，…，wn，未及时拦截目标对我造成的损失为λw1，λw2，…，λwn（λ为权重与损间的比例系数）。最晚拦截时间分别为t1，t2，…，tn，上级指定优先拦截的目标集，目标Mj（j=1，2，…，n）的拦截剩余时间tlsgj（j=1，2，…，n），且拦截剩余时间与权重满足一致性关系，也就是当tlsgi≤tlsgj时，wi≤wj。并设sj为拦截目标Jj的防空导弹发射时间，pj为导弹拦截目标Jj的实际拦截时间，Uj为未杀伤目标对我造成的单位损失，cj为导弹与目标Jj的遭遇时间，满足cj=sj+pj。因目标Jj（j=1，2，…，n）必须在杀伤区内被杀伤，因此，最晚必须在tlsgj-pj之前开始发射导弹。若cj＞tlsgj，则目标未被杀伤，可能投弹对我攻击，因此，发生拦截延误，记Uj=1，对我造成损失为λwjUj，若cj≤tlsgj，则未发生拦截延误，记作Uj=0，此时未对我地面目标造成损失，即λwjUj= 0。问题是确定一个拦截方案，使得在上级指定目标不延误条件下，对我造成的总损失∑λwjUj最小。

3.3 算法

3.3.1 引理

本文考虑单目标通道拦截目标问题，在拦截剩余时间与权重满足一致性关系，且保证上级指定目标不延误条件下，使总损失∑λwjUj最小化，把这一问题简称为加权一致损失决策问题。

下面利用引理说明“加权一致损失决策问题”有最优解的必要条件。

引理3加权一致损失决策问题有最优解的必要条件是T为不延误目标子集。

3.3.2 算法

步骤1：设指定目标集E0=T，记l=n-|T|，其中|T|表示T中的目标个数，记非上级指定目标集M/T=；

步骤3：若k=l+1，算法终止，（El，M/El）就是最优的目标拦截排序；若k＜l+1，转步骤4；

步骤4：按照拦截两个连续跟进目标的条件，

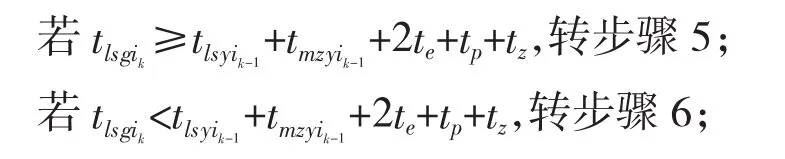
步骤7：按照Ek中确定的目标顺序进行拦截，当有新目标出现或原有目标未被毁伤，转步骤1。3.3.3 算法分析

引理4 算法3.3.2所产生的拦截目标排序是加权一致损失决策问题的最优解。证明较为复杂，证明思想与方法可参考文献［6］。

4 实例

下面以总损失最小化模型为例说明。

假设某次要地防空作战中，先后有8批目标进入发射区（方便起见，不妨设每批目标的数量都为1），我防空导弹火力单元共有2个目标通道，防空导弹的平均速度为1 100 m/s，空袭目标的相关数据如表1所示。

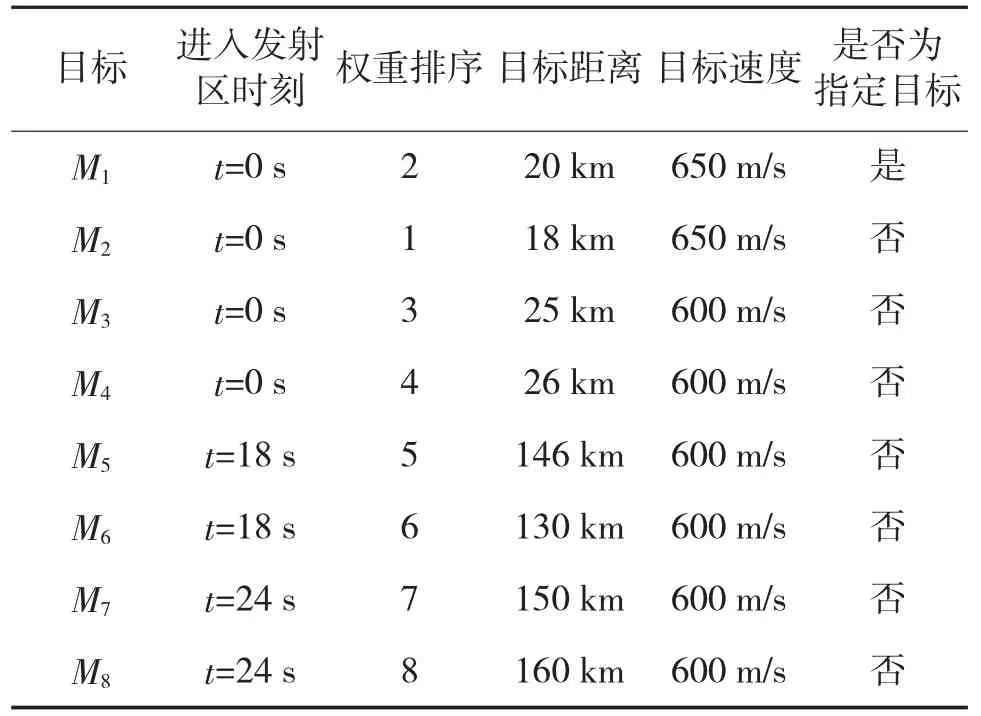
表1 空袭目标相关数据

根据算法时刻t=0 s，上级指定的目标T={M1}，需要拦截的其他目标E=M/T={M2，M3，M4}。计算目标M1，M2，M3，M4的拦截剩余时间tlsg1=11.4 s，tlsg2=10.2 s，tlsg3=14.7 s，tlsg4=15.2 s，此时目标通道全部空闲，因目标M1是指定目标，必须优先拦截，所以可以用通道1拦截目标M1，设导弹发射时间间隔总和为16 s，因目标M2，M3，M4的拦截剩余时间都小于16 s，所以目标M2，M3，M4中必然有两个目标会发生拦截延误，此时M4的权重最大，所以安排通道2拦截目标M4，M2，M3放弃拦截。在时刻t=18 s时，目标M5，M6进入发射区，t=24 s时M7，M8进入发射区，拦截剩余时间分别为 tlsg5=85.8 s，tlsg6=76.4 s，tlsg3=88.2 s，tlsg4=94.1 s，都能得到有效拦截，所以t=18 s时，分别安排通道1和2拦截目标M5，M6，t=34 s时，再安排通道1和2拦截目标M7，M8。

5 结束语

通过算法2.3.2、3.3.2和实例4，可以得出：

（1）对上级指定的优先拦截目标，实施优先拦截；（2）不能有效毁伤的目标不拦截；（3）威胁值大的目标，优先拦截；（4）一次拦截未被毁伤的目标，还在下次拦截的目标范围之内，可实施2次拦截；（5）先来目标不一定先拦截；（6）拦截花费的总时间最短（由2.3.2的步骤6.1可得）。

与现有的准则对比，可以看出，算法既体现了现有的拦截原则，比如对上级指定的目标实施优先拦截，优先拦截威胁值大的目标等；同时也考虑了实际情况，先到不一定先拦截，不能有效毁伤的目标不拦截等，保证在目标函数最优的前提下使得拦截总时间最短，并且两算法都是最优算法。但这里研究的主要是单目标通道拦截决策问题，模型也只考虑单一的目标函数，对于更为复杂的多目标通道和多目标函数的拦截决策问题是今后需进一步研究的方向。

［1］娄寿春.地空导弹射击指挥控制模型［M］.北京：国防工业出版社，2009.

［2］丁勇军，刘法明，郭宝金.空袭目标威胁判断的模糊聚类分析［J］.弹箭与制导学报，2006，26（1）：324-326.

［3］徐品高.防空导弹火力单元对空中目标的拦截排序问题［J］.战术导弹技术学报，2007（2）：1-9.

［4］高建军，赵瑞峰，郭强.指定目标不延误条件下的防空导弹火力单元拦截排序研究［J］.防空兵学院学报，2013（4）：53-54.

［5］徐品高.关于防空导弹的连续射击能力问题［J］.战术导弹技术学报，1996（3）：1-7.

［6］陈小林.带权的误工排序问题的最优算法［J］.运筹与管理学报，2009，18（3）：41-45.

［7］苏永英，蒋宗彩，孙叶平.推广的误工排序问题的最优算法［J］.上海第二工业大学学报，2008，25（3）：201-206.

［8］张鑫，张丕旭.防空导弹中末制导交班成功概率评估方法［J］.四川兵工学报，2013，34（3）：41-44.

［9］Sidney J B．An Extension of Moore’s Due Date Algorithm［J］．Symposium on the Theory of Scheduling and Its Applications，1973（1）：393-398.

Intercept Decision Algorithm for Specified Targets without Delay

GAO Jian-jun，HAN Jin-cheng，LIU Guan-ying，GUO Qiang，CUI Yan-li
（Air Defense Forces Academy，Zhengzhou 450052，China）

Proceed from the existing interception sort criteria，combining with the characteristics of incoming targets，and applying modern sorting theory，dinamic decision-making model and the totle minimization model are established respectively，and giving the corresponding optimal algorithm. Finally，the example tells that models and algorithms derived in this paper embodies the existing interception criteria，but also on the promotion of the existing guidelines.

menace estimate，intercept scheduling，air defense missil，fire unit

N945.12；N945.13

A

1002-0640（2015）07-0071-04

2014-04-05

2014-06-07

全军军事学研究生基金资助项目（2010JY0534-296）

高建军（1978- ），男，山西临县人，硕士，讲师。研究方向：系统优化与决策分析。