Application of surface-heat-flux estimation by measuring model interior temperature in hypersonic wind tunnel tests

张石玉, 赵学军, 陈则霖

(中国航天空气动力技术研究院, 北京 100074)

Application of surface-heat-flux estimation by measuring model interior temperature in hypersonic wind tunnel tests

A series of hypersonic wind tunnel tests are implemented to estimate the aero-heating flux of a test plate. The heat flux at the heated surface is not directly measured, but is estimated by solving an inverse heat conduction problem (IHCP) based on measured temperature at the back surface or inside of the plate. The most outstanding advantage of this method is that the temperature sensors do not contact with the high temperature outflow directly, but are embed ded inside the plate. Therefore, it provides an alternative approach to estimate the high temperature surface heat flux for practical hypersonic vehicle flight tests. The primary aim of this paper is to verify the applicability of this method to predict the flow characteristics of the outflow filed. The hypersonic wind tunnel tests are implemented in FD-03 WT of China Academy of Aerospace Aerodynamics (CAAA). Some tests apply a smooth plate in general hypersonic wind tunnel tests; and others adopt a test plate bounded with a trip line to interrupt the boundary layer of the plate. As shown in the heat flux estimated results, severe changes in the outflow such as shock waves caused by the trip line can be predicted by the estimated heat flux.

inverse heat conduction problem;surface heat flux;estimation;aerothermodynamics;wind tunnel test

0 Introduction

The aero-heating effect of a hypersonic aircraft cannot be ignored. As the Mach number increases, the temperature in the boundary layer on the hypersonic aircraft surface could increase to thousands of degrees centigrade. It is very difficult to measure the aero-heating heat flux directly at such high temperatures by applying general sensors such as Schmidt-Boelter gage , coaxial thermocouples and general heat flux sensors[7]. These sensors are always attached on the heating surface and would be easily destroyed by high temperature outflow. In order to solve this problem, one available method to estimate the surface heat flux is to embed temperature sensors inside the thermal insulation layer, and use the measured temperatures to estimate the surface heat flux. Such an approach is based upon the principle of Inverse Heat Conduction Problem (IHCP)[8-12].

Cai[1], Zhou[11],and Coy[12]applied the IHCP to evaluate the heat flux by adopting simulation data. The heat flux in Ref.[12] is described by a polynomial model, which is impractical under general hypersonic vehicle flight conditions. Practical situation is that the heat flux value is transient and changing with time. The Sequential Future-Information (SFI) method is used in this paper to predict the initial heat flux, which changes with time and is dependent on the priori heat flux.

Qian[13]and Mehta[10]applied a similar method for electrical heating tests and combustion tests to estimate the heat flux at the heating area, and achieved reasonable results.

In Ref.[2], we adopted the surface heat flux estimation method for hypersonic aero-heating wind tunnel tests in CAAA to estimate the aero-heating heat flux, the result of which is inaccordance with the result of empirical methods. Based on this research, this paper is aimed to verify the applicability of estimated heat flux to predict the outflow field characteristics.

The basic physical mechanism and mathematical method of heat-flux estimation method are introduced in Section one, and a series of hypersonic aero-heating tests at wind tunnel FD-03 of CAAA are displayed in Section two. Then surface-heat-flux of test plate is estimated and analyzed to demonstrate the usefulness of the heat-flux estimation method in hypersonic flight tests in Section three.

1 Heat-flux estimation mechanism

Utilizing inside temperature measurements to estimate boundary heat flux is an inverse heat conduction problem (IHCP) as described in Ref. [14] and Ref. [15]. The flow chart of this estimation method is shown in Fig.1. The general process could be simplified as “Prediction & Correction”. At the beginning, the initial heat flux on the upwind surface is predicted. Then the temperature inside the plate can be calculated via the heat conduction simulation codes. Then, according to the error criterion from an optimization algorithm, the corrected heat flux is estimated. After that, repeat the heat conduction calculation applying the corrected heat flux as a new boundary condition, and iterate the above processes until the error criterion is satisfied.

Fig.1 Flow chart of heat flux estimation

Many literatures indicate that the estimation process of IHCP is unstable, as illustrated in Ref. [14-15]. It means that small errors in temperatures will lead to large errors in the heat flux. Consequently, Finite Impulse Response (FIR) low-pass filter is adopted to preprocess the measured temperature to reduce the high frequency noises before the heat-flux estimation.

In following sections, the heat transfer model, heat-flux estimation criterion and optimization algorithm will be introduced briefly.

1.1 Heat transfer model

Figure 2 shows a one-dimensional heat transfer model of the shell of a hypersonic flight vehicle, whereinOYrepresents the heated surface,OXis the thickness direction of the shell, anddis the thickness. Assuming that the temperature gradient in the direction ofOYcan be ignored, the heat transfer model can be simplified to a one-dimensional heat conduction model. Take the upwind surface as the heat-flux boundary and the back surface as the isolation boundary, the one-dimensional heat transfer function can be expressed as follows:

(1)

and the boundary conditions as,

Whereλdenotesthethermalconductivityoftheshell,ρdenotesthedensityandCpisthespecificheatratio.TheinitialtemperaturedistributionalongOXisT0(x).Theheatedsurfacex=0 is set to be the heat-flux boundary asQ(0,t).Thebacksurfacewherex=dis set to be the isolation boundary. The finite difference method is used to solve such partial differential equations.

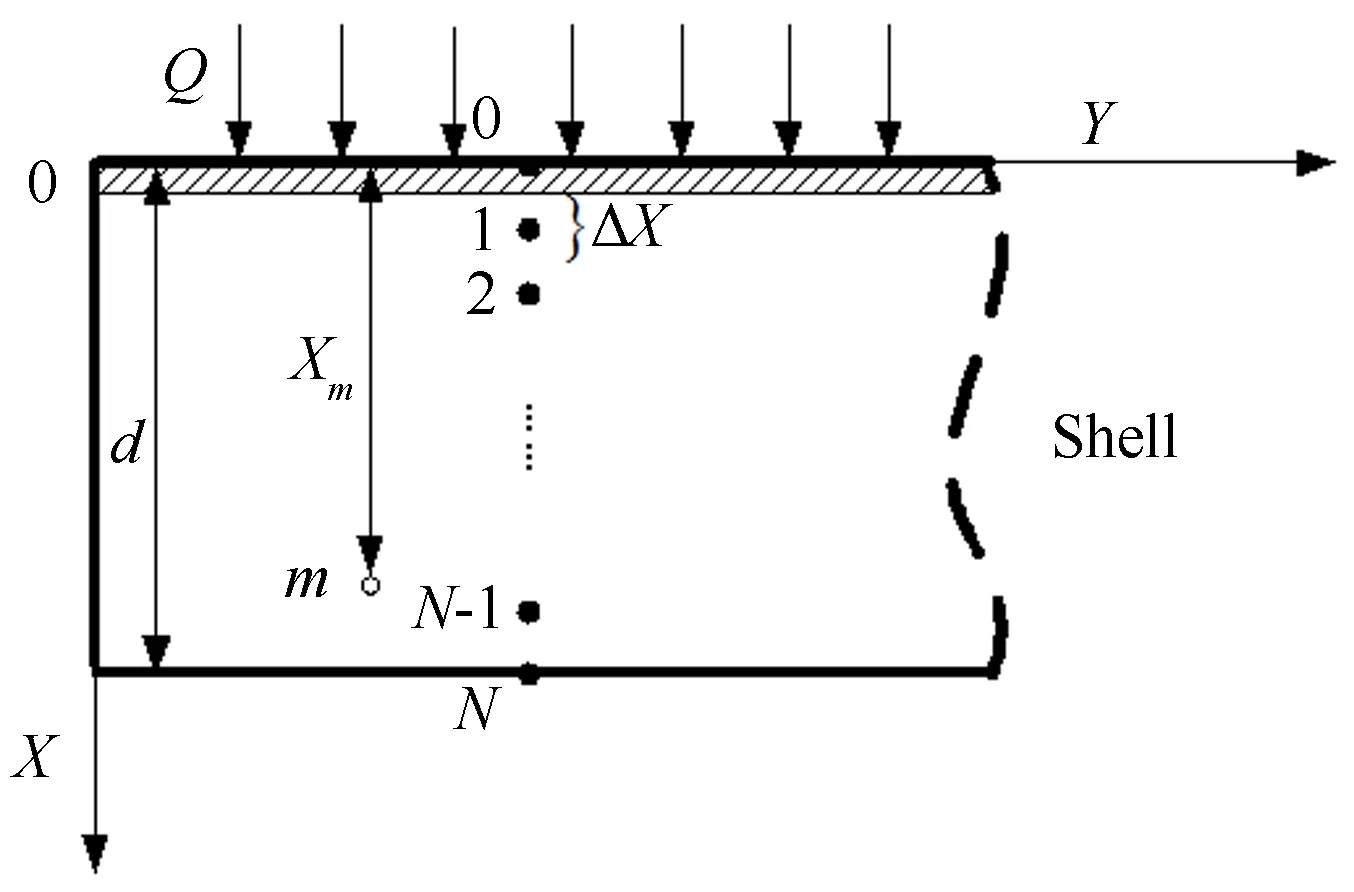
Fig.2 Sketch of one dimensional heat transfer model in a shell of hypersonic flight vehicle

图2 高超声速飞行器壳体一维热传导模型

1.2 Heat-flux estimation criterion and optimization algorithm

Sequential Future-Information (SFI) method developed by James V. Beck[9]is applied to predict the initial heat flux at the beginning of a time step. Considering the time steptM,theheatfluxispredictedbyrtime steps aftertM.HeatfluxoftimestepM+1 toM+ris initialized by the following function.

(2)

The estimation criterion is selected as temperature-error criterion, which is the sum of squares of residual errors between measured and calculated temperatures inrtime steps[1], as follows.

(3)

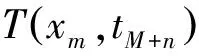
Intheoptimizationprocess,Newton-Raphson(NR)minimizationalgorithmisusedtocorrecttheheatfluxQ. The NR optimization function is given as follows,

(4)

Wherekandk+1 denote the optimizing steps.

The whole estimation process can be simplified as follows: firstly, the initial heat flux ofQ0should be initialized by Eq. (2), and then the NR optimization function of Eq. (4) is applied to iterate the heat fluxes of the nextrsteps, thatQ0toQ0+r, until the relative error of temperature-error-criterionJ(Eq. (3)) is convergent. Then turn to the next time step to iterate the new heat flux. Details of this estimation process can be found in Ref. [1] and Ref.[2].

2 Hypersonic wind tunnel tests

The previous study of heat-flux estimation method in standard plate heating tests refers to the research of Qian Weiqi etc.[13]. They inserted an electric resistance into a test plate to heat the plate, aiming to verify the experimental precision of this technology.

In previous research of CAAA, a series of hypersonic wind tunnel tests were implemented to verify the reliability of the method for wind tunnel tests. All of these research results can be found in Ref. [2]. These tests were implemented in FD-03 Wind Tunnel of CAAA, which is an intermittent hypersonic scientific research wind tunnel, can operate at four Mach numbers, asMa5, 6, 7 and 9, and the stagnation temperature is from 358K to 1028K.

The test model is a flat plate made of aluminum alloy with the size of 390mm×180mm×30mm. The width of the test plate is equal to that of the inflow section of the wind tunnel, in order to ensure the entire upwind surface of the test plate in a homogeneous flow field. Meanwhile, in order to reduce the heat dissipation, the test plate is packed with isolation materials around except for the upwind surface. Nickel chrome-nickel silicon thermocouples are embedded into the test plate to measure inner temperatures, with measurement error of 0.75%×temperature(℃).

The wind tunnel is operated atMa5 in tests, with stagnation temperature of nearly 481K and the environment temperature of nearly 281K.

A series of tests are implemented, including general tests and trip-line tests. A photograph of a general test is shown in Fig.3, and a trip-line test picture is shown in Fig.4. The trip line is bounded between the 7thand the 8ththermocouples, and the diameter of the trip line is 1.5mm. The primary states of experiments are shown in Table 1.

表1 风洞试验及实验模型主要状态参数

Fig.3 Picture of test chamber in wind tunnel with test plate installed

图3 风洞试验安装图

Fig.4 Picture of test plate with a trip line tied up

The photograph of the back surface and the sketch of embedded thermocouples are shown in Fig.5(a) and Fig.5(b) respectively. It can be seen that there are 14 thermocouples, while the 1stto the 13ththermocouples are installed inside the plate and the depth is 15mm. Meanwhile, the distance between two thermocouples is equal in the outflow direction. And the 14ththermocouple is installed on the back surface, between the 6thand the 7ththermocouples, as a validation measurement. The analysis of the thermocouples can be found in Ref. [2].

It should be noticed that, there are two Data Acquisition Units (DAUs) used to acquire temperature data. The 1stto the 7ththermocouples are connected to DAU A. The others are connected to DAU B. As the test results indicate, the collected data of DAU A and B are with non-negligible bias. In order to eliminate this bias error, this paper utilizes the data acquired by DAU A only.

Fig.5 Sketch of embedded thermocouples in test plate

3 Estimation results and heat flux analysis

In the wind tunnel tests, the primary three factors that strongly affect the estimated heat flux are described as follows: firstly, the characteristics of outflow field, secondly, the inflow temperature, and thirdly, the initial temperature of the test plate. In order to prove the applicability of the estimated heat flux to analyze the characteristics of the outflow field, it is necessary to reduce the influence of the second and the third factors. For the second factor, as there is an inflow heater in front of the inflow section, it is enssured that the inflow temperature could be controlled nearly at the same temperature. But the initial temperature of the test plate is hard to control precisely in practice due to the limitation of test instruments and test time. As a result, the initial temperatures of the same thermocouple are not identical in different tests, with deviations of nearly 0.3 to 0.6K, which means that it is necessary to choose those tests whose initial temperatures are as close as possible to eliminate the influence of different initial temperatures. After comparing all tests data, two groups of tests are selected to estimate the aerodynamic heat flux whose initial temperatures are close to each other. The first test group contains two general tests as test 1 and test 2, and the second group contains a general test and a trip-line test as test 3 and test 4, as shown in Fig.6.

Initial temperature curves of the 1stto the 7ththermocouples in selected tests are shown in Fig.6, where test 1, test 2 and test 3 are general tests, and test 4 is a trip-line test.

Fig.6 Initial temperatures of the 1st to the 7th points in four tests

The surface heat fluxes estimated by the 1stthermocouple for the four tests are shown in Fig.7. As the figure shows, the start times of the wind tunnel in the four tests are not the same. Meanwhile, the durations of steady periods in the four tests are different too (It is controlled by researchers but not so exactly in every tests. But it does not influence the heat flux analysis, as interpreted in Ref.[2]). At the same time, the four test measurement curves can be divided into four stages. The first stage is the initial period. As the wind tunnel test does not start, the heat flux in this period is nearly zero. When the wind tunnel turns on, a high heat flux period arises which is named as starting-peak period. After almost 20 seconds, the test develops to the steady period, while the heat flux keeps constant. At last when the heat flux is raised in every curve, it develops to the wind tunnel turn-off period (The detailed introduction of the heat flux peak can be found in Ref. [2], too.). In order to analyze the outflow characteristics, the average value of the heat flux curve at the early 40 seconds in the steady period is analyzed because the average heat flux is more stable and the trend of the heat flux is clearer.

Fig.8 is the comparison of the average heat flux values from the early 40s of the steady periods of test 1 and test 2. From this figure, it can be concluded that:

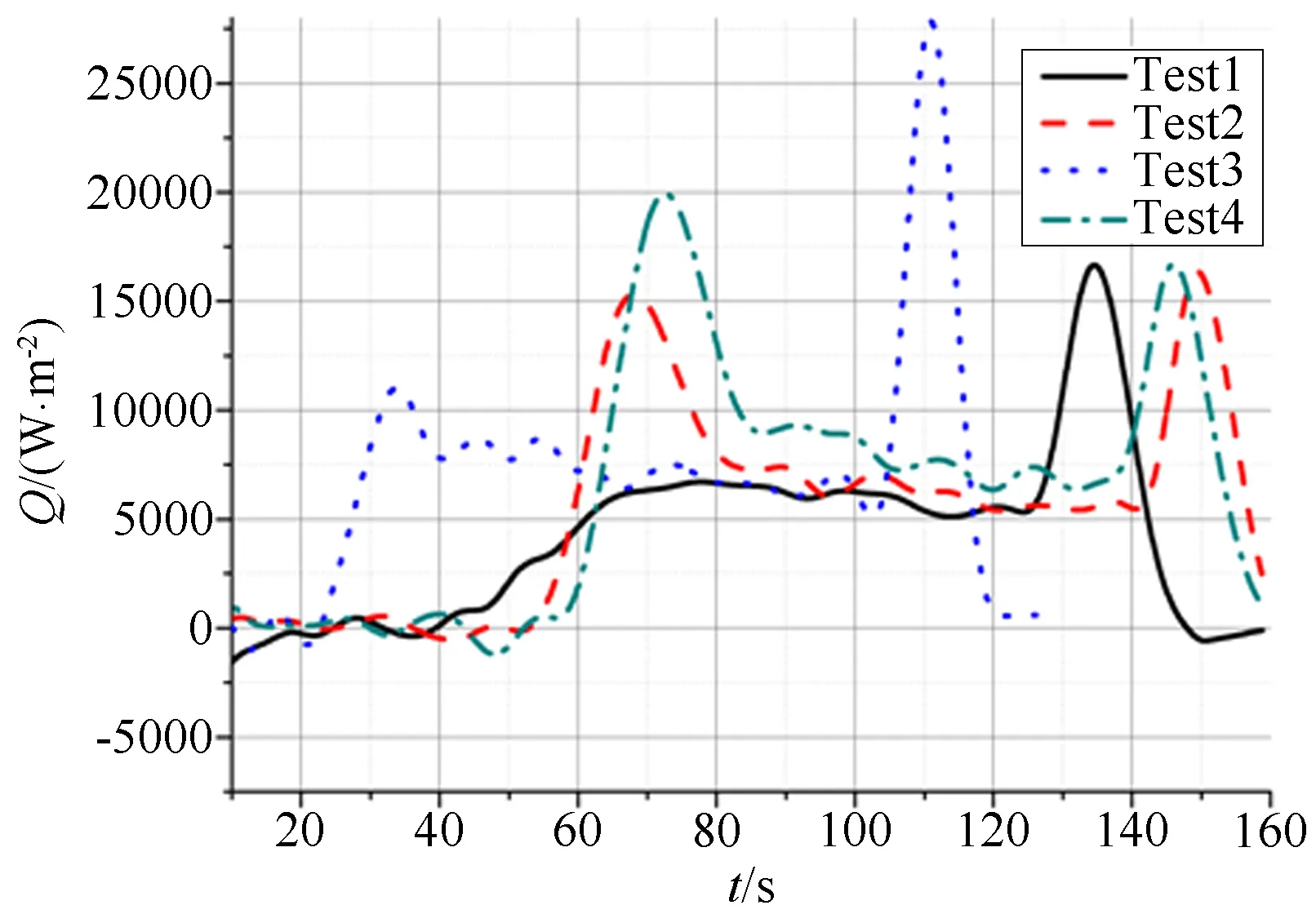
Fig.7 Comparison of estimated heat flux of the 1st point

Fig.8 Heat-flux average of test 1 and test 2 at the early 40s in steady period

图8 试验1和试验2稳定段前40s热流均值

(1) Each curve of this figure shows that the heat flux is decreasing from the 1stto the 7ththermocouple, which is opposite to Fig.6, as the initial temperature is increasing. It means that when the initial temperatures of the thermocouples are increasing, the heat flux is decreasing. It is in coincidence with the heat conduction theory. These results indicate that the initial temperature is the dominant factor that determines the trends of heat flux curves in general tests.

(2) Comparing two curves of test 1 and test 2, it can be seen that the differences of heat fluxes at the same thermocouple between two tests are approximately identical. Meanwhile, the initial temperature differences in Fig.6 at the same point are nearly identical, too. It means that the heat flux in general tests is estimated with good consistency.

Fig.9 is the average heat flux results of test 3 and test 4 from the early 40s of the steady stage.

As shown in Fig.9, the heat flux curve of test 4 is absolutely different from that of test 3. Although the initial temperatures of these two tests in Fig.6 are close, the heat-flux curve of test 4 is with a significant difference to that of test 3. From this figure it can be concluded that:

Fig.9 Heat flux average of test 3 and test 4 at the early 40s in steady period

图9 试验3和试验4稳定段前40s热流均值

(1) The heat flux of the 7ththermocouple is much larger than the measurement result before. As previously mentioned, test 4 is designed to bind a trip line between the 7thand the 8ththermocouples. It is supposed that the trip line is the primary factor that causes the high heat flux to the 7ththermocouple. As a proof, the schlieren picture in Fig.10 displays that there is an oblique shock in the outflow near the trip line. As we know, the heat flux before the shock wave would grow up strongly. This result indicates that the estimated heat flux can be used to predict intensive changes in the flow field. In addition, it can be extended that the surface-heat-flux estimation can be used to solve many problems, for instance, to search transition location, to identify shock wave indirectly, to evaluate the strong changes in outflow field, etc.

Fig.10 Schlieren photograph of test4 in steady period

(2) As previously mentioned, considering that there is no trip line in test 4, the heat flux should be higher than that in test 3. But the estimated results indicate that from the 2ndto the 6thmeasurement the heat flux of test 4 is smaller than that of test 3. Meanwhile, the gradient of this heat-flux curve is larger than the curve of test 3. As we presumed, the reason is that the shock wave may interfere with the boundary layer in the forward distance. This conclusion needs to be verified in further research.

At last, the estimated heat flux of test 4 indicate that when there is a shock wave in the flow field, the flow characteristics are the dominant factor that strongly influence the heat flux.

4 Conclusions

Surface-heat-flux estimation is applied to estimate the aerodynamic heat flux of a test plate in hypersonic wind tunnel tests. A series of tests are implemented to study the applicability of the estimated heat flux to predict the outflow characteristics, including general tests and trip-line tests. The results indicate that the estimated heat flux can be utilized to identify the intensive changes in the outflow. As a conclusion, the surface-heat-flux estimation method of this paper could be used as follows: (1) to estimate the aero-heating flux of hypersonic and high temperature flow fields, (2) to analyze complex hypersonic flow fields, (3) to identify the location of the boundary layer transition point, (4) to validate thermo-protection schemes, etc.

In future research, it is necessary to develop two-dimensional and three-dimensional heat-flux estimation methods to improve the ability to analyze the whole aero-heating area.

[1] Cai Jinshi. Aircraft system identification[M]. Beijing: China Astronautic Publishing House, 1995.

[2] Zhang Shiyu, Ma Yuanhong, Zhao Xuejun. The experimental study of heat-flux identification technology for hypersonic aero-thermodynamics[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(5): 33-37.

[3] Coblish J J, Davenport A H. Recent efforts at AEDC’s Von Karman facility and hypervelocity wind tunnel 9 to enhance facility compatibility[R]. AIAA-2002-2787, 2002.

[4] Kidd C T, Adam J C. Development of a heat-flux sensor for commonality of measurement in AEDC hypersonic wind tunnels[R]. AIAA-2000-2514, 2000.

[5] Coblish J J, Coulter S M, Norris J D. Aerothermal measurement improvements using coaxial thermocouples at AEDC hypervelocity wind tunnel No.9[R]. AIAA-2007-1467, 2007.

[6] Bezuidenhout J J, Schetz J A. Heat flux determination using surface and backface temperature histories and inverse methods[R]. AIAA-2001-3530, 2001.

[7] Smith R H, Scott E P, Ligrani P M. Experimental validation of an inverse heat conduction problem using thermocouple and infrared data[R]. AIAA-2001-0507, 2001.

[8] Imber M, Khan J. Prediction of transient temperature distributions with embedded thermocouples[J]. AIAA Journal, 1972, 10(6): 784-789.

[9] Osman A M, Beck J V. Nonlinear inverse problem for the estimation of time-and-space-dependent heat-transfer coefficients[J]. Journal of Thermophysics, 1989, 3(2): 146-152.

[10] Mehta R C. On the estimation of combustion gas temperature and convective heat transfer coefficient[R]. AIAA-2007-806, 2007.

[11] Zhou J H, Zhang Y W, Chen J K, et al. Inverse heat conduction using measured back surface temperature and heat flux[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(1): 95-103.

[12] Coy E B. Measurement of transient heat flux and surface temperature using embedded temperature sensors[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(1): 77-84.

[13] Qian Weiqi, Wu Shijian, Bu Haitao, et al. Preliminary investigation of principle experiment for aero-thermodynamic parameter estimation[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(2): 59-62.

[14] Frankel J I. Regularization of inverse heat conduction by combustion of rate sensor analysis and analytic continuation[R]. AIAA-2006-1184, 2006.

[15] Frankel J I. Regularization of inverse heat conduction by combination of rate sensor analysis and analytic continuation[R]. AIAA-2006-1184, 2006.

Author biography:

Zhang Shiyu(1984-),male, born in Suining, Sichuan Province, Engineer. Engaged in aircraft aerodynamic parameter identification and aero-thermal heat flux estimation research. Address: Mailbox 7201-56, Beijing, China. E-mail: zhangsy701@sina.com.

(编辑：张巧芸)

1672-9897(2015)02-0061-07

ZhangSY,ZhaoXJ,ChenZL.Applicationofsurface-heat-fluxestimationbymeasuringmodelinteriortemperatureinhypersonicwindtunneltests.JournalofExperimentsinFluidMechanics, 2015, 29(2): 61-67. 张石玉, 赵学军, 陈则霖. 采用内部测温估计表面热流在高超声速风洞试验中的应用. 实验流体力学, 2015, 29(2): 61-67.

Zhang Shiyu*, Zhao Xuejun, Chen Zelin

(China Academy of Aerospace Aerodynamics, Beijing 100074, China)

表面热流预估方法利用试验件内部的温度来预估其表面热流。该方法的最大优点是测量温度的热电偶是内埋在试验件内部，不与外界的高温气流直接接触。该方法为高超声速飞行器飞行实验估计表面热流提供一种可行的途径。为了验证该方法在预测外界流场特性方面的能力，在航天空气动力技术研究院(CAAA)的FD-03风洞中开展了一系列高超声速气动热风洞试验。试验中采用一块铝合金试验板，部分试验采用光滑平板，其余试验在试验平板的表面添加拌线以干扰外界流场。而后采用热流估计方法预估试验板的表面热流。预估结果表明，如由拌线产生的激波等外流场的强烈变化将在估计的热流结果中得到清晰的显示。

热传导逆问题；表面热流；估计；气动热；风洞试验

V211.71

A

10.11729/syltlx20140089

date: 2014-07-27;Revised date:2015-01-20

采用内部测温估计表面热流在高超声速风洞试验中的应用

张石玉, 赵学军, 陈则霖

(中国航天空气动力技术研究院, 北京 100074)

*Corresponding Author E-mail: zhangsy701@sina.com