条(环)状干摩擦阻尼器的微滑移数值模型*

赵宁，蔺彦虎(西北工业大学机电学院，陕西西安710072)

条(环)状干摩擦阻尼器的微滑移数值模型*

赵宁，蔺彦虎
(西北工业大学机电学院，陕西西安710072)

提出一种求解弹性条(环)状阻尼器微滑移接触运动的数值方法。将阻尼器和外部激励历程在空间和时间上离散，将相同数量的干摩擦触点布置于离散阻尼器上；把接触运动判据应用到各离散接触点，确定其运动状态并修正刚度矩阵，求解整个阻尼器的平衡方程。该方法避免了有限元软件求解含摩擦接触问题的迭代过程，从而保证了求解的可执行性。同时，克服了微滑移模型理论解法对法向载荷分布规律及载荷时变性的限制，为求解具有局部性以及时变性的法向载荷的结构动态响应提供了更为精确的边界条件，从而可提高结构频响分析的准确性。应用多谐波平衡法分别计算宏滑移和微滑移阻尼器约束下的结构动态响应，发现在结构减振中，微滑移模型能够适应更宽范围的法向力。

干摩擦阻尼器；微滑移；接触运动；多谐波平衡法；动响应

由于结构简单、在高温及复杂环境的稳定性及优良的减振性能，干摩擦阻尼器被广泛应用于工程中。如为了降低筒形结构的航空发动机的篦齿封严装置振动幅值，在其定子或转子上安装有阻尼环或阻尼套筒；航空发动机的叶-盘系统中，叶片设计有凸台，通过振动时凸台间的挤压和相对运动来降低叶片振动幅值；航空薄壁齿轮上安装的阻尼环等结构［1］，均是应用干摩擦进行结构减振的实例。

叶片减振结构中，凸台面积以及凸台间的法向力较小，可将其简化为单对触点，进行非线性结构的动响应求解［2］。然而，对于安装阻尼环、阻尼套筒的结构，由于接触面积大，加上筒状结构进行周波型振动或者盘状结构进行节径型振动时，将引起不同接触部位的法向力变化，局部法向力可能会变得较大，这时还将阻尼器与结构间的作用通过单对接触点来表示，将不符合阻尼器与结构间的实际。

微滑移模型用多对触点来表达其与结构间的局部摩擦作用，Menq［3-4］建立了考虑微滑移效应的矩形杆模型，杆与结构间分布有厚度可忽略的剪切层，用该剪切层模拟阻尼器和结构表面微观凸起，给出了接触运动以及干摩擦力的理论解［3］，并将该理论解应用于结构动态响应计算，并与实验结果［4］对比，验证了该模型的准确性。徐自力［5］将该模型引入叶片减振分析，并分析了最优正压力的影响因素。Csaba［6］的微滑移模型忽略了Menq模型中的剪切层，用单元节点切向刚度模拟阻尼器的切向刚度。Menq与Csaba模型均采用解析法求解，法向力分布为特定形式，不可时变，激励力或激励位移也被设定为谐波形式。这些假设往往不符合应用中的载荷分布以及变化特性，具有一定的局限性。

商用有限元软件应用迭代法求解含摩擦的接触问题，迭代过程实际上是确定触点运动状态的过程。有限元软件能较好地模拟含摩擦的局部接触作用，并对结构做时域内的响应分析，然而，多数商业有限元软件，如Ansys、Abaqus等均不能用来做非线性频响分析，而非线性频响求解又是薄壁结构减振设计的重要内容。马晓秋［7］用谐波法描述干摩擦力，将干摩擦力等效为结构内阻，用Ansys软件计算了叶片频响。然而一阶谐波法是一种近似方法，不能准确表达接触运动的粘-滑效应，等效方法对求解的准确性也有一定影响。因此有必要针对阻尼器具体结构，发展出能够方便求解接触运动的数值模型，将其应用于非线性频响分析，摆脱应用有限元软件求解接触问题的束缚。

本文将Yang［8］发展的宏滑移模型黏滞—滑移—分离判据应用于微滑移模型，形成了求解微滑移接触运动的数值方法。相比微滑移模型理论解法，该方法对微滑移模型法向载荷分布规律及其时变性没有限制，同时取消了Menq［3］模型中防止刚体位移的限位弹簧，可对刚体位移进行准确求解。求解过程无须迭代，从而保证求解的可执行性。最后，应用多谐波平衡法(Multiple Harmonic Balance Method，MHBM)计算微滑移数值模型约束下的结构动响应，以证实所发展模型的实用性，并分析了宏滑移模型和微滑移模型对结构动响应影响的异同。

1 Yang模型及算例

1.1 Yang宏滑移模型

相比于微滑移模型，对宏滑移模型的研究较多，也较为成熟。Sanliturk和Ewins［9］发展了一种求解宏滑移模型的“轨迹跟踪法”，该方法将求解周期离散为若干时间点，对每一时间步的运动状态进行判断，确定运动状态后，计算出相应状态下的位移量及干摩擦力。重复进行以上步骤，即可得到整个周期内的触点运动状态及干摩擦力，一般地，跟踪过程只需维持两个周期，即可得到稳定的运动状态。单颖春［10］应用类似方法计算叶片动响应，并与实验值对比，取得了很好的效果。

Yang于1998年发表文章［8］详细讨论了宏滑移模型的运动状态确定以及状态判定依据，并假设激励为谐波形式时运动状态的转换角。所建立的滑移模型如图1所示。

图1中，body1和body2表示两接触物体，通过触点表示两者的作用力，body2可运动也可固定。n0表示初始法向力；ku，kv分别为切向及法向刚度；u，v分别为切、法向运动；f表示干摩擦力；μ为干摩擦系数；w表示触点切向运动；n表示法向力。两接触体可能存在3种运动状态，黏滞、滑移或分离状态，在接触运动周期内，这几种状态可能会相互转化，如表1所示。

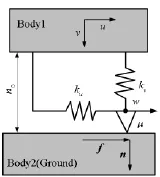
图1 Yang接触运动模型Fig.1 Yang’s contact kinematicmodel

表1中，“E”表示黏滞状态，“P”表示正向滑动，“N”表示反向滑移，“S”表示分离状态，“当前”表示当前时刻触点的运动状态，“后继”表示运动状态从当前到下一时刻的转化。

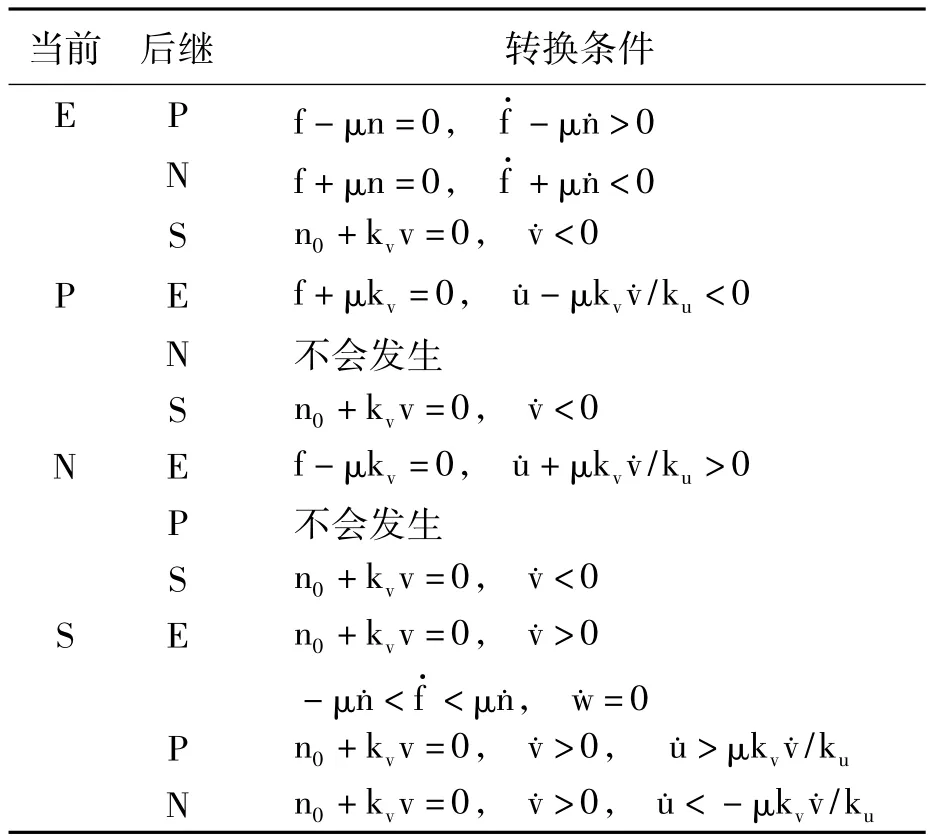
表1 运动状态转化条件Tab.1 Translation criterion of kinematic state

干摩擦力遵循Coulomb摩擦定律，即

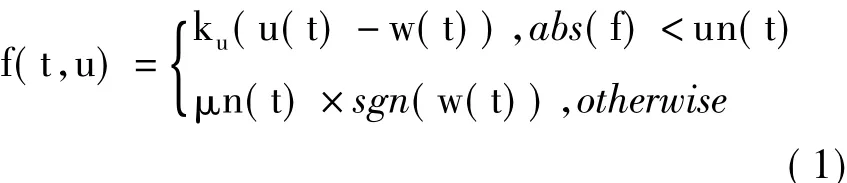
式中，sgn为符号函数，abs为绝对值符号，t为时间。

1.2 宏滑移接触运动模型算例

选取图1中“body1”的运动参数如表2所示，“body2”固定不动，求解该模型。求解时将周期离散，按表1中所示的“当前状态”，计算运动状态参数及力值，然后依据表1中的不等式，判定是否发生了运动状态转化，如果转化，则按照新的状态求解各参量，如果未发生状态转化，则计算下一个时刻各参数。计算取摩擦系数μ为0.5，t代表离散时间点。

结果如图2所示，图中每列为表2中计算参数的运动状态、力及滞回环。可以看出应用Yang发展的判据可求解复杂的运动状态。从图2第二行可以看出在运动过程中，两物体遍历了分离—黏滞—滑移运动，所以该行的第三列所示的滞回环中有相当一部分值为0。第三行表示在平面内的运动频率不同时的运动状态，类似于李萨如的运动形式，这时摩擦力及滞回曲线显得更为复杂，平面内y向运动频率为x向的3倍，所以滞回环也呈现出这种关系。

表2 宏滑移模型计算参数Tab.2 Parameters ofmacro-slip model

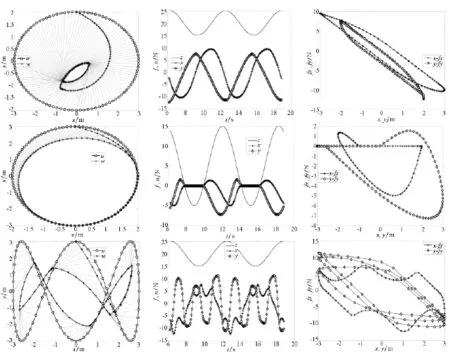
图2 运动状态、力及滞回曲线Fig.2 Curve of kinematic state，force and hysteresis

2 微滑移数值模型及求解方法

2.1 条(环)状阻尼器的离散

工程中经常用到的阻尼器为环状或条状结构，如阻尼环、阻尼块。干摩擦模型的建立是为了研究法向力存在时的切向运动及受力，故适合用杆模型等效条状阻尼器［3］。图3(a)为Menq［3］建立的微滑移模型，在阻尼块与结构的接触面上布有剪切层，用来模拟接触面的切、法向力学行为。该模型认为，当接触体表面粗糙度足够小时，将接触表面均匀划分为若干块，尽管各分块的凸起和凹陷形貌不尽相同，然而，从统计学的角度看，他们表现出来的力学行为是相同的。因此剪切层的不同部位具有相同的切、法向刚度。

用数值方法对微滑移理论模型求解的第一步是对阻尼器离散。根据求解问题，在Menq模型底部预设一定数量触点来替代剪切层，将模型均匀离散，离散数量与触点数相同，如图3(b)所示。由于均匀离散，各触点的力学特征相同，所以触点切向刚度Ku相等。条(环)状阻尼器法向尺寸远小于接触平面尺寸，法向力引起的弯曲效应较小，可将法向力作用直接施加在触点上。若阻尼器为开口环或条状阻尼器，则连接第n块与第1块的弹簧将不存在，对于整体环，则弹簧存在。图中fn，x(t)(x=1，2，…，n)表示法向载荷，该载荷可时变。k为离散单元间的刚度。

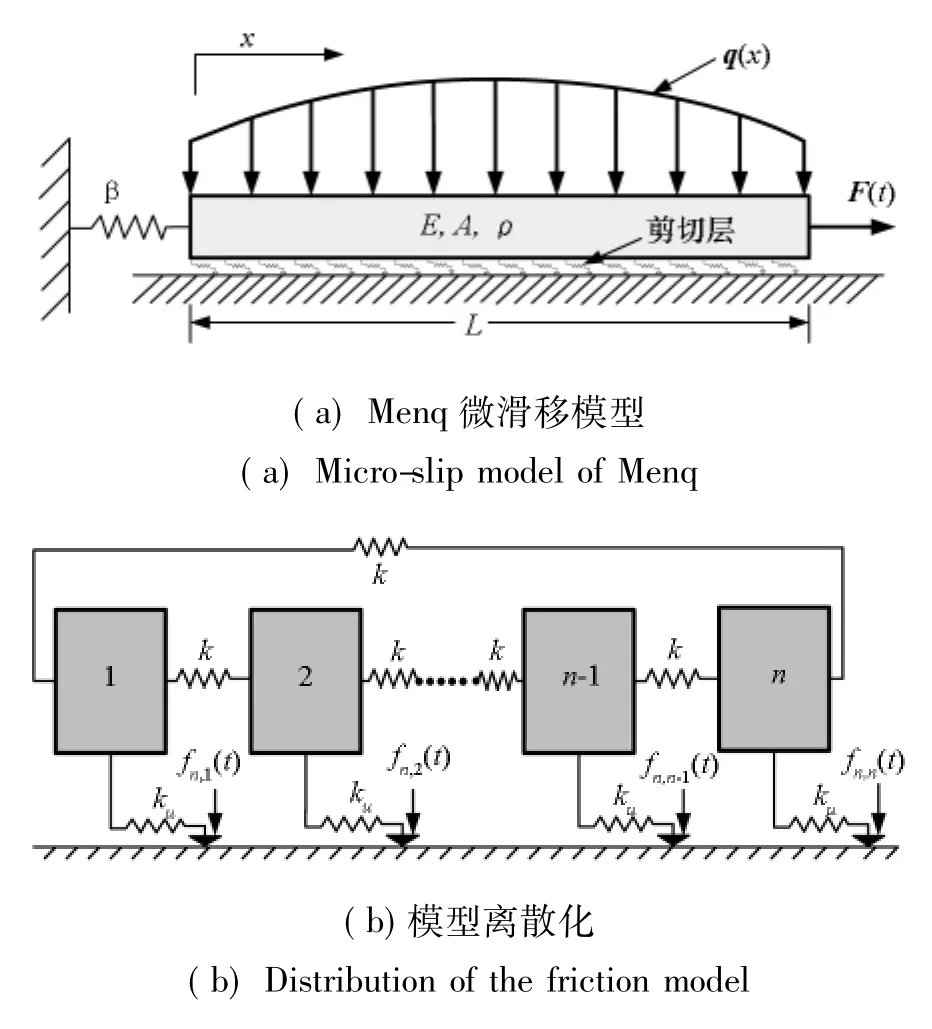
图3 Menq微滑移模型及其离散Fig.3 Menq’smicro-slipmodel and its discretization

2.2 求解流程

与宏滑移模型相似，求解微滑移模型也需要在求解周期内离散。

如图3(b)所示，假设在第1号离散体上作用位移载荷，则该位移载荷也可被离散为有限多个值，用uj和d uj表示j时刻的位移以及j+1时刻与j时刻的位移变化量。用Fi，j表示触点i在j时刻的受力，d Fi，j表示第j+1时刻与j时刻触点i受力变化量。类似地，用wi，j和d wi，j表示触点位移量及其变化量，用xi，j和d xi，j表示离散段的位移量及其变化量。用s表示u，F，x，w则有

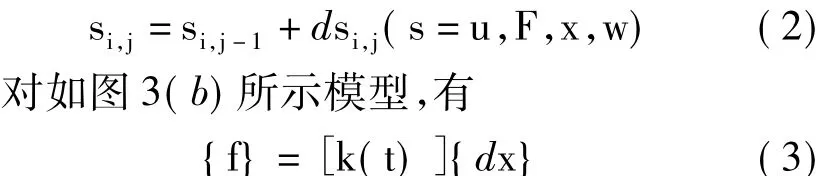
d x为一向量，表示离散位移增量，长度等于离散体个数。k(t)为离散体刚度矩阵，呈带状，是时变量:黏附于离散体的触点(如第q个触点)处于黏滞时，刚度矩阵对应的k(q，q)值为k(q，q)= 2k+ku，ku为剪切刚度，如图3(b)所示。若处于滑移或分离状态时，对应节点的刚度值为k(q，q) =2k。需要注意的是，由于激励形式为位移激励，因此在任何时间点上任何离散块体都处于受力平衡状态，即每个离散块体所受合力为0，故f为0向量，注意式(3)中的f是各离散体所受合力，不是摩擦触点的受力。求解结果有可能出现阻尼器的刚体位移，这取决于位移载荷的大小和法向力值。图4给出求解流程，图中i表示干摩擦触点，j表示离散时间点。

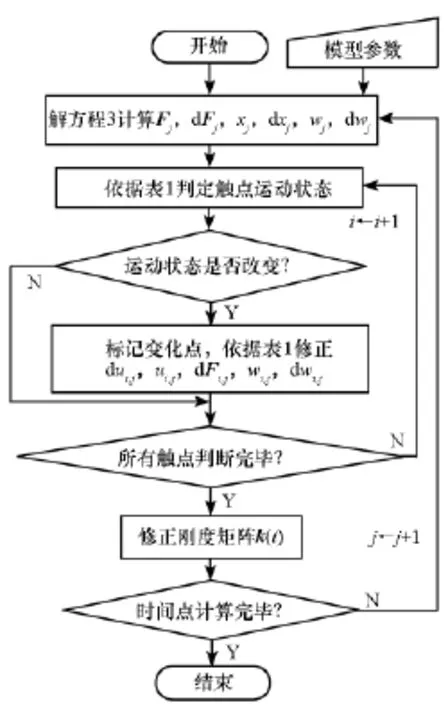
图4 微滑移模型计算流程Fig.4 Flowchart of solving micro-slip model

3 算例

3.1 算例1均布载荷的整体环状阻尼器

图5所示的整体环状阻尼器，与图3(a)相比，除了结构与载荷变化外，做了两个调整:一是激励形式变为位移形式，带来的好处是可以求解刚体位移，既可求解出整体滑移也可求解出局部滑移。在阻尼器实际工作中，也属位移激励的情形，摩擦力伴随接触运动产生。二是解除了防止阻尼器产生刚体位移的弹簧β，对原模型的假设限制进一步减少。

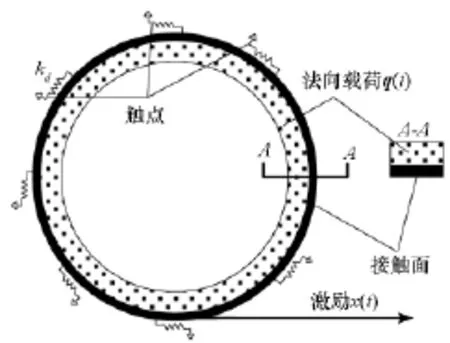
图5 均布载荷的环状阻尼器Fig.5 Circular damper with uniform load

如图5所示，阻尼环横截面为矩形，弹性模量E=2.07×105MPa，宽b=30mm，阻尼环内径r= 140mm，外径R=150mm，μ=0.5，切向刚度kd按Mindlin［11］理论计算。激励取x(t)=0.31sin(2πt)，方向沿环的切向，法向力q(t)=137N，t为离散时间点，将结构均匀离散，得到图6所示的滞回环。

如图6所示，离散数取n=1时，阻尼器模型为宏滑移模型，由于未考虑阻尼器本身的弹性变形，其滞回环的斜率最大。其求解结果与跟踪求解［9］方法一致，当n逐步增大时，求解结果越逼近微滑移模型理论解，当离散数n=15时，数值模型的滞回曲线与理论解重合，已经足够接近理论解［3］了。在激励历程中，微滑移触点逐次滑移，最终达到整体滑移，形成刚体运动。

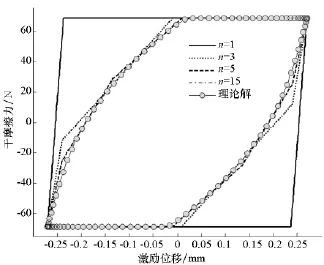
图6 微滑移模型滞回环Fig.6 Hysteresis curve ofmicro-slip model

3.2 算例2非均布载荷

如图7所示，阻尼器横截面为矩形，杨氏模量与宽度，即干摩擦系数同算例1，高h=3mm，激励x(t) =0.32sin(2πt)，长L=80mm；载荷呈抛物线状，最大值分布于两端，均为34.5N，最小值为5N。

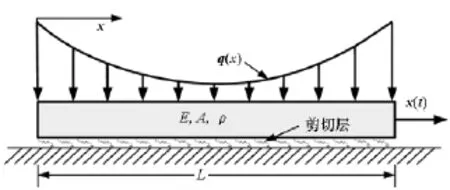
图7 非均布载荷模型Fig.7 Modelwith non-uniform load

求解阻尼器离散为15段，得到如图8所示的滞回环。从滞回环可以看出，该模型在激励下并未发生刚体滑动，只是产生了局部滑移。

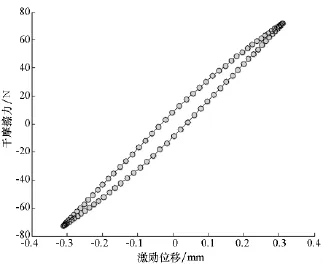
图8 非均布载荷下的滞回环曲线Fig.8 Hysteresis curve of non-uniform load

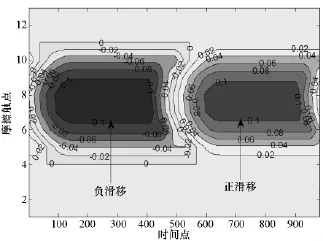
图9滑移等值线图Fig.9 Contourmap of slip

图9 为各摩擦触点在一个运动周期内的滑移量等值线图，可以看出8号触点的滑移量最大，成为滑移核心，结合图7，可以发现这是由于法向载荷较小造成的；等值线图不是关于点8对称而是偏向于编号小的触点，这是由于计算中考虑了阻尼器的变形以及切向载荷的位置共同造成的。1～4号触点及11～15号触点一直处于黏滞状态，所以模型呈部分滑移状态，与图8的结论是一致的。

该计算流程还可以求解法向力时变条件下的微滑移接触运动及干摩擦力，也可计算有分离运动的实例。限于篇幅，这里不再给出算例。

4 MHBM法计算计及微滑移的结构动响应

具有干摩擦约束的结构呈现出强边界非线性，传统的数值积分方法由于计算耗时太长而不能满足结构设计过程所要进行的频响分析。因而人们发展出了摄动法，谐波平衡法，加辽金法等。经研究［12］，应用MHBM法结合Fourier变换及其逆变换法求解含干摩擦的动响应问题，具有足够的准确度和求解速度。本文用该方法结合快速Fourier变换及快速逆Fourier变换法，计算计及微滑移的结构动态响应。

4.1 多谐波平衡法

图10为一装有微滑移阻尼器的振动模型，该模型可用来表示航空发动机涡轮叶盘B-D型减振器。M，C，K分别表示质量、阻尼和刚度。fex(t)为激振力，q为阻尼器法向载荷。其控制方程为

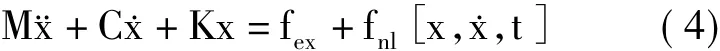
式中fnl［x，˙x，t］为由阻尼器产生的非线性力。谐波平衡假设认为，在周期性载荷作用下，系统的响应也是周期的，因此可用傅里叶序列表示

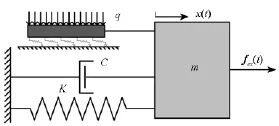
图10 装有微滑移阻尼器的振子模型Fig.10 A vibratormodelwith a micro-slip damper

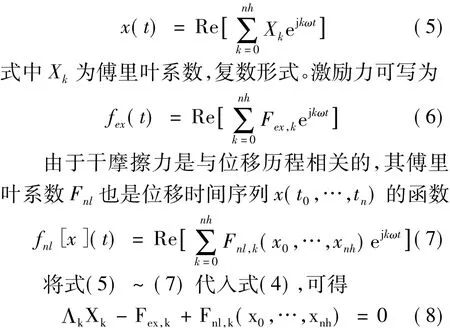
式中Λk=-(kω)2M+j kωC+K，为动刚度矩阵。

求解时，首先对位移序列傅里叶系数进行傅里叶逆变换，得出时域位移值，用该位移序列求解干摩擦力，之后对干摩擦力进行傅里叶变换，得到干摩擦力在频域内的谐波系数值。最后对位移序列的傅里叶系数值迭代，直到满足式(8)为止。式(8)为一非线性方程，需用迭代方法求解，Newton法及其衍生格式是求解该方程的基础。本文采用Broyden法求解。

4.2 计算结果

选取表3所列的计算参数，分别应用微滑移模型和宏滑移模型计算结构动响应。

表3 计算参数表Tab.1 Parameters used in the calculation

微滑移模型计算的频幅响应如图11所示，图中Fn为法向载荷，即图10中的q，计算微滑移模型离散为15段，切向刚度求解用Mindlin［11］理论。

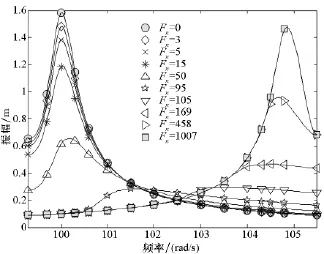
图11 微滑移模型结构频响图Fig.11 Frequency response of structure withmicro-slip model

求出宏滑移模型频响后，即可对比两者减振性能的差异。如图12所示，法向力较小时，微滑移模型与宏滑移模型的效果相差无几，微滑移模型对振动的抑制效果稍差于宏滑移模型，这主要是微滑移模型考虑了阻尼器的弹性形变而显示出切向刚性不足，不能给结构提供足够的干摩擦力约束振动幅值。随着法向载荷的增加，则显示出大的差异:采用宏滑移模型时，阻尼器很快处于黏滞状态，这时可等效为一弹簧，因此随着法向力的进一步增加，结构振动幅值基本不再增加；而微滑移模型考虑了结构的局部滑移，阻尼器仍未完全黏滞，因此可以提供不同幅值的干摩擦约束力，从图6也可以观察出这一点。直到法向载荷增加至1007N，微滑移模型所有触点才完全黏滞，达到与宏滑移模型相同的振动幅值。由于在较大法向载荷下仍有触点可以滑动，因此微滑移模型在较大法向载荷时，仍具有较明显的减振效果。

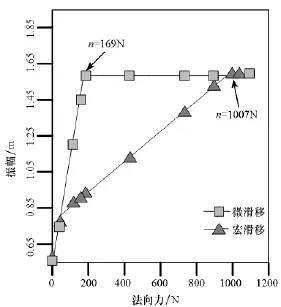
图12 宏、微滑移模型减振效果对比Fig.12 Contrast between themacro-slip model and themicro-slip model

Griffin［13］的用宏滑移迟滞模型为航空发动机叶片B-D型阻尼器建模，计算了叶片的频响及动应力，并搭建实验台验证计算结果的可靠性。计算及实验结果如图13所示［13］。图13为两种不同刚度的阻尼器在不同法向力下叶片的动应力。文献［13］未给出叶片及阻尼器的几何及力学参数，因此无法用本文发展的微滑移模型计算其动响应。但观察其计算结果与实验结果可发现:法向力值较低时，实验结果和计算结果相符合；但随着法向力的增加，实验值与计算值出现偏离，尤其是在阻尼器刚度较小的条件下，并且法向力较大时，动应力的计算值总是大于实验值。

切向刚度较大时，阻尼器更像是一个刚体，因而可用宏滑移模型描述，其计算结果与实验值相差不大；当切向刚度较小时，阻尼器在整体滑动之前更容易产生局部滑移，这时如果还用宏滑移模型来描述阻尼器，则会在法向力较大时无法计及局部滑移而使得计算值偏大。对比图12，当法向力增大时，使用宏滑移模型计算的结构频响值会很快上升，而使用微滑移模型的频响值上升缓慢。可见用微滑移模型，动应力计算结果会缓慢上升，因而更加接近于实验值。这也说明使用微滑移模型可为结构提供更加精确的边界条件，使结算结果更符合实际；微滑移模型能够在更宽的法向力范围为结构提供振动幅值衰减，从而使动应力计算值降低。

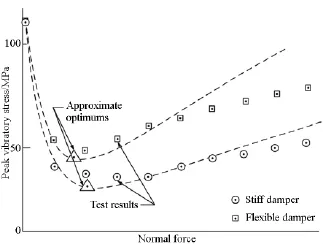
图13 Griffin计算结果与实验结果对比Fig.13 Contrast between calculation result and test result of Griffin

5 结论

1)依据Yang发展的单触点分离—接触—滑移判据，求解了不同法向力及不同牵引切向运动时，干摩擦触点的运动状态及干摩擦力。

2)将Yang判据应用于条状或环状微滑移模型，形成了求解微滑移触点运动状态及受力的数值方法，通过与理论模型对比，检测了算法的准确性。该方法克服了理论模型对于方向载荷分布及激励条件的诸多假设，拓宽了微滑移模型的应用范围，可为结构减振计算提供更加真实的边界条件，同时该求解方法无须迭代，从而避免了有限元软件求解含摩擦接触的收敛问题。

3)用MHBM法分别求解了宏滑移及微滑移阻尼器约束的结构动响应。结果表明，在法向力较小条件下，两者相差不大，随着法向力的增加，两者减振效果出现明显差别，微滑移模型对法向力的适应能力更强，可在较宽法向载荷范围内达到结构减振的目的。

References)

［1］晏砺堂，朱梓根，李其汉，等.高速旋转机械振动［M］.北京:国防工业出版社，1994.YAN Litang，ZHU Zigen，LI Qihan，et al.Mechanical vibration with high rotational speed［M］.Beijing:National Defense Industry Press，1994.(in Chinese)

［2］单颖春，郝燕平，朱梓根，等.干摩擦阻尼块在叶片减振方面的应用与发展［J］.航空动力学报，2001，16(3): 218-223.SHAN Yingchun，HAO Yanping，ZHU Zigen，et al.Application and development of platform friction damper for depressing resonant vibration of blades［J］.Journal of Aerospace Power，2001，16(3):218-223.(in Chinese)

［3］Menq C H，Bielak J，Griffin JH.The influence ofmicroslip on vibratory response，part I:a new microslip model［J］.Journal of Sound and Vibration，1986，107(2):279-293.

［4］Menq C H，Bielak J，Griffin JH.The influence ofmicroslip on vibratory response，part II:a comparison with experimental results［J］.Journal of Sound and Vibration，1986，107(2): 295-307.

［5］徐自力，常东锋，上官博.微滑移离散模型及在干摩擦阻尼叶片振动分析中的应用［J］.机械科学与技术，2007，26(10):1304-1307.XU Zili，CHANG Dongfeng，SHANGGUAN Bo.One-bar microslip discrete model and its application to vibration analysis of blade with dry friction damper［J］.Mechanical Science and Technology for Aerospace Engineering，2007，26(10):1304-1307.(in Chinese)

［6］Csaba G.Forced response analysis in time and frequency domains of a tuned bladed disk with friction dampers［J］.Journal of Sound and Vibration，1998，214(3):395-412.

［7］马晓秋，王亲猛，张锦，等.带干摩擦阻尼结构叶/盘系统动力学分析［J］.航空动力学报，2002，17(1):110-114.MA Xiaoqiu，WANG Qinmeng，ZHANG Jin，et al.Dynamic analysis of bladed disc systems with vibrational dampers［J］.Journal of Aerospace Power，2002，17(1):110-114.(in Chinese)

［8］Yang B D，Chu M L，Menq C H.Stick-slip-separation analysis and non-linear stiffness and damping characterization of friction contacts having variable normal load［J］.Journal of Sound and Vibration，1998，210(4):461-481.

［9］Sanliturk K Y，Ewins D J.Modeling two-dimensional friction contact and its application using harmonic balance method［J］.Journal of Sound and Vibration，1996，193(2): 511-523

［10］单颖春，朱梓根，刘献栋.凸肩结构对叶片的干摩擦减振研究-规律分析［J］.航空动力学报，2006，21(1):174-180.SHAN Yingchun，ZHU Zigen，LIU Xiandong.Investigation of the vibration control by frictional constraints between blade shrouds-rule analysis［J］.Journal of Aerospace Power，2006，21(1):174-180.(in Chinese)

［11］Mindlin R D.Compliance of elastic bodies in contact［J］.Journal of Applied Mechanics，1949，16:259-268.

［12］Wang JH，Chen W K.Investigation of vibration of a blade with friction damper by HBM［J］.Journal of Engineering for Gas Turbines and Power，1993，115(2):295-299.

［13］Griffin J H.Friction damping of resonant stresses in gas turbine engine airfoils［J］.Transactions of the American Society of Mechanical Engineers，Journal of Engineering for Power，1980，102:329-333.

A numericalmodel for the bar or circular m icro-slip dry friction damper

ZHAO Ning，LIN Yanhu
(College of Mechanical，Northwestern Polytechnical University，Xi’an 710072，China)

A numericalmethod to solve the contact kinematic problems of elastic bar or circularmicro-slip dry friction damper was proposed.Firstly，the damper and the time course of external excitation were discretized in the space and time domain respectively，and the same number of contact points was attached to the discrete damper.Secondly，the determination criterion of the contact kinematic state of the contact point pairswas used to each contact pair，and the stiffnessmatrix of the damper wasmodified.Thirdly，the whole balance equation with the new stiffnessmatrix was solved in each time step.Differing from the way the finite element software dealing with the contact problem with friction，the iteration was avoided，thus the feasibility of the solution was guaranteed.Meanwhile，the restriction of the distribution and the time variability of the normal load was overcome，and therefore it provided a more accurate boundary condition for solving dynamic response of structure.Lastly，the response of structures constrained by themacro-slip and micro-slip damper were computed by the MHBM(Multi Harmonic Balance Method)respectively and the distinctness of the solution was analyzed.Results show that themicro-slip model damper can have a broader normal force range for vibration reduction.

dry friction damper；micro-slip；contact kinematic；multiharmonic balancemethod；dynamic response

TH133

A

1001-2486(2015)05-067-08

10.11887/j.cn.201505011

http://journal.nudt.edu.cn

2014-10-15

国家自然科学基金资助项目(51075328)

赵宁(1958—)，男，广东广州人，教授，博士，博士生导师，E-mail:zhaon@nwpu.edu.cn