基于计算机求解土的先期固结压力

彭 静, 张胜军, 何 娇, 蒋晓娟, 周蕙娴

(水利部 长江勘测技术研究所,湖北 武汉 430011)

基于计算机求解土的先期固结压力

彭 静, 张胜军, 何 娇, 蒋晓娟, 周蕙娴

(水利部 长江勘测技术研究所,湖北 武汉 430011)

在研究卡萨格兰德(Casagrande)经验作图法的基础上,采用等跨度圆弧求圆半径及拉格朗日多项式插值法求取最小曲率半径Rmin点的计算思路,通过Matlab语言编制相应的计算程序求取先期固结压力pc值。结合膨胀土算例表明该方法对试验数据具有较好的适应性,且操作简便,能以图形化方式显示确定先期固结压力,避免人为误差,计算速度快,还可将研究成果拓展到其他需要做大量数据统计、图形绘制和分析的应用领域中。

先期固结压力;卡萨格兰德法;最小曲率半径;Matlab语言

土体先期固结压力pc是指天然土层在历史上所经受的最大竖向固结压力,是判断土体应力历史的一个重要指标,在不同的应力历史状况下土层的变形分析中,它也是一个重要的计算参数[1]。

pc的推求方法大致有3种[2]：Casagrande方法(1936年)、布麦斯脱方法(1940年)、薛迈脱曼方法(1955年)。目前,卡萨格兰德法因其简单易行而成为确定pc的普遍方法,也是规范中采用的方法,这种方法是利用e-lgp曲线曲率突变点来推求先期固结压力的。

本文以南阳膨胀土为研究对象,选取Casagrande方法,在分析了既有e-lgp曲线数学模型不足的基础上提出了一种用计算机确定先期固结压力pc值的方法,即利用Matlab语言编写了相应计算程序,将试验数据导入计算机即可求解得到土体先期固结压力pc值,并自动完成图解画图,可以消除目测定点的人为性,提高求解精度,取得较满意的结果。

1 先期固结压力计算方法研究

1.1 国内外研究现状

先期固结压力pc的确定,最常用的方法是卡萨格兰德(Casagrande,1936年),它依据室内高压固结曲线,寻找最小曲率半径点,然后以经验图解法求得。为提高Casagrande法确定先期固结压力的精确度,许多学者提出了不同的改进方法,如波密斯德(Burmister,1942年)建议的确定pc方法、三笠氏“ Cc” 法、施默特曼(schmertmann,1966年)以及国内一些学者也相应提出“ F” 法、割线平移法以及快速固结试验法等。通过大量的试验研究和pc曲线作图,确定先期固结压力pc,用卡萨格兰德法最为简单,试验数据获取快,得出的pc值也比较适当。

求解先期固结压力e-lgp曲线,由试验所得数据描点并用圆润的曲线段连接而成,其关键是确定曲线的最大曲率点,而常规的手工作图法凭肉眼找出该点,对作图比例的依赖性较大,而且切线、角平分线等绘制繁杂,很容易引起人为误差,也很难用直接拟合的数学函数描述或近似其变化规律。

目前,有很多学者对使用计算机确定土体先期固结压力进行研究。如刘用海采用3次多项式和最小二乘法回归拟合压缩曲线直接求其曲率函数的方法推求pc值[3]。刘衍成用相邻三点得两条直线段比较相邻直线斜率变化幅度大小的方法确定曲率最大点得到pc值(以下简称斜率变化法)[4]。张书宪提出相邻三点逐一比较圆半径的大小确定曲率最大点(以下简称三点定圆法)[5]。周国云采用先对试验数据点插值后以三点求圆半径比大小的方法(以下简称插值后三点定圆法)[6]。

1.2 计算机求解先期固结压力存在的问题

根据卡萨格兰德的经典图解法,以实验室固结压力试验数据所描绘的离散点为基础而连接成的圆滑e-lgp曲线,理论上该曲线是呈顺时针弯曲的,而且原始的试验数据点与整条曲线的特性存在很大的关联性,采用多项式拟合或插值法得到的曲线会丢失原始试验数据点或使曲线发生顺时针和逆时针交替弯曲的状态,而且在数据间隔较大的曲线段拟合曲线和插值曲线明显较卡萨格兰德法所得曲线弯曲程度要大,这些都改变了卡萨格兰德的方法所得e-lgp曲线的特征,如图1所示：

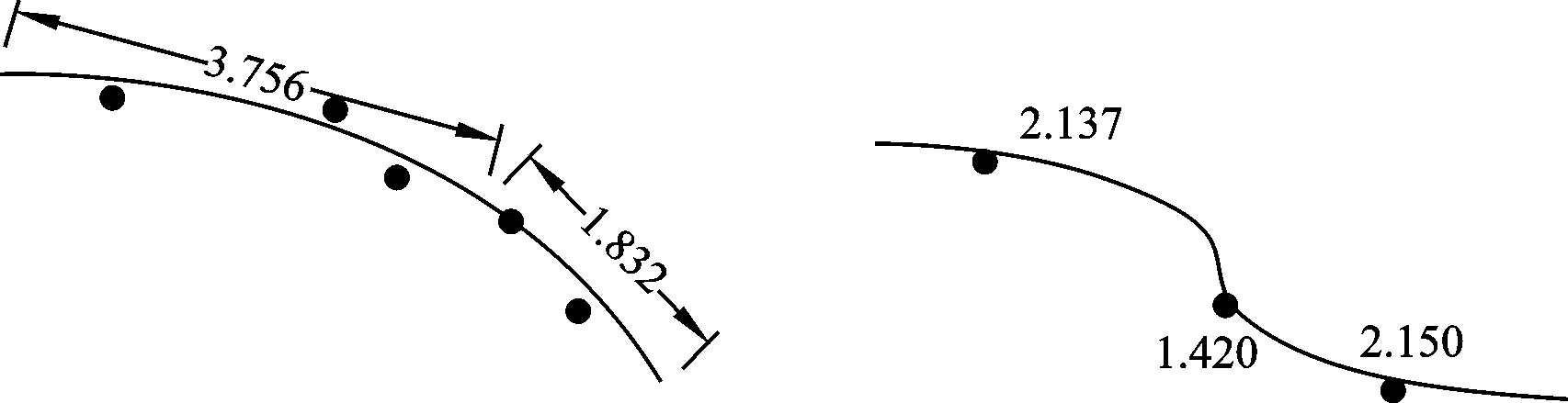
图1 拟合曲线和插值曲线相对原始试验数据点的特征变化Fig.1 Variation characteristics of experimental data points in fitting curve and interpolation curve

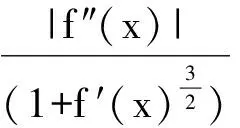
采用斜率变化法、三点定圆法以及插值后三点定圆法,也会由于试验数据点分布的间距不一受到干扰,间距很近的3个数据点,中间点位置的变化对所确定的圆弧半径或两直线斜率的影响程度明显要比间距较大的情形要大得多(图2)。

图2中左边由间距大的点构成的圆弧,当中间点偏移形成新圆弧时,新旧两圆弧的曲率变化幅度不大;右边相距较近的三点构成的圆弧,当中间点偏移形成新圆弧时,新旧两圆弧的曲率变化幅度很大。由于试验数据或多或少的存在着误差,这些描点时的偏差会使上述现象总是存在。这类现象会使斜率变化法、三点定圆法以及插值后三点定圆法在试验数据点密集的区域产生错误判断,且称为局部误判现象。假设图2右边图形为卡萨格兰德经典作图法的前固结压力的e-lgp曲线,用斜率变化法、三点定圆法以及插值后三点定圆法判断弯曲程度最大的点明显在末端的小圆弧的中间点处,而从先期固结压力的定义以及卡萨格兰德图解法的实际意义出发,需要找出e-lgp曲线整体趋势上一个产生最大弯曲变化的点,凭经验可以判断该点应在大圆弧中间一点附近。因此斜率变化法、三点定圆法以及插值后三点定圆法三种方法仍存在很大缺陷。

图2 不等间距三点确定圆弧曲率Fig.2 Curvature determined by unequal spacing of three-point

2 先期固结压力求解及自动作图

要真正实现用计算机求解卡萨格兰德经典图解法求解土体先期固结压力的工程实践问题,需要保持卡萨格兰德经典图解法图形的几何特性,设计出遵从其图解原理的一种新算法。

2.1 最小曲率半径Rmin的确定

采用等跨度(圆弧起始点和终止点在横轴方向上间距相等)圆弧求圆半径,比较找到最小半径的圆弧段确定曲率最大点所在的范围,克服局部误判现象。具体圆弧分段如图3：

图3 试验数据点在e-lgp曲线上的分布示意图Fig.3 Distribution chart of experimental data points of e-lgp curve

试验采用逐级加荷方式,压力值(单位kPa)分别为25,50,100,200,300,400,600,800,1 200,1 600,2 400,3 200(取对数后的刻度为1.398,1.699,2.000,2.301,2.477,2.602,2.778,2.903,3.079,3.204,3.380,3.505),取对数后分别对应e-lgp曲线中A,B,C,D,E,F,G,H,I(最后三点确定直线趋势线,图中未画出)的横坐标,先等跨度取圆弧定圆比较半径选出半径最小圆弧,则由该组数据描绘的e-lgp曲线的曲率最大点就在所得圆弧上。如图4等跨度三点取圆弧可得到五段圆弧,进而可得圆弧半径的求解公式为：

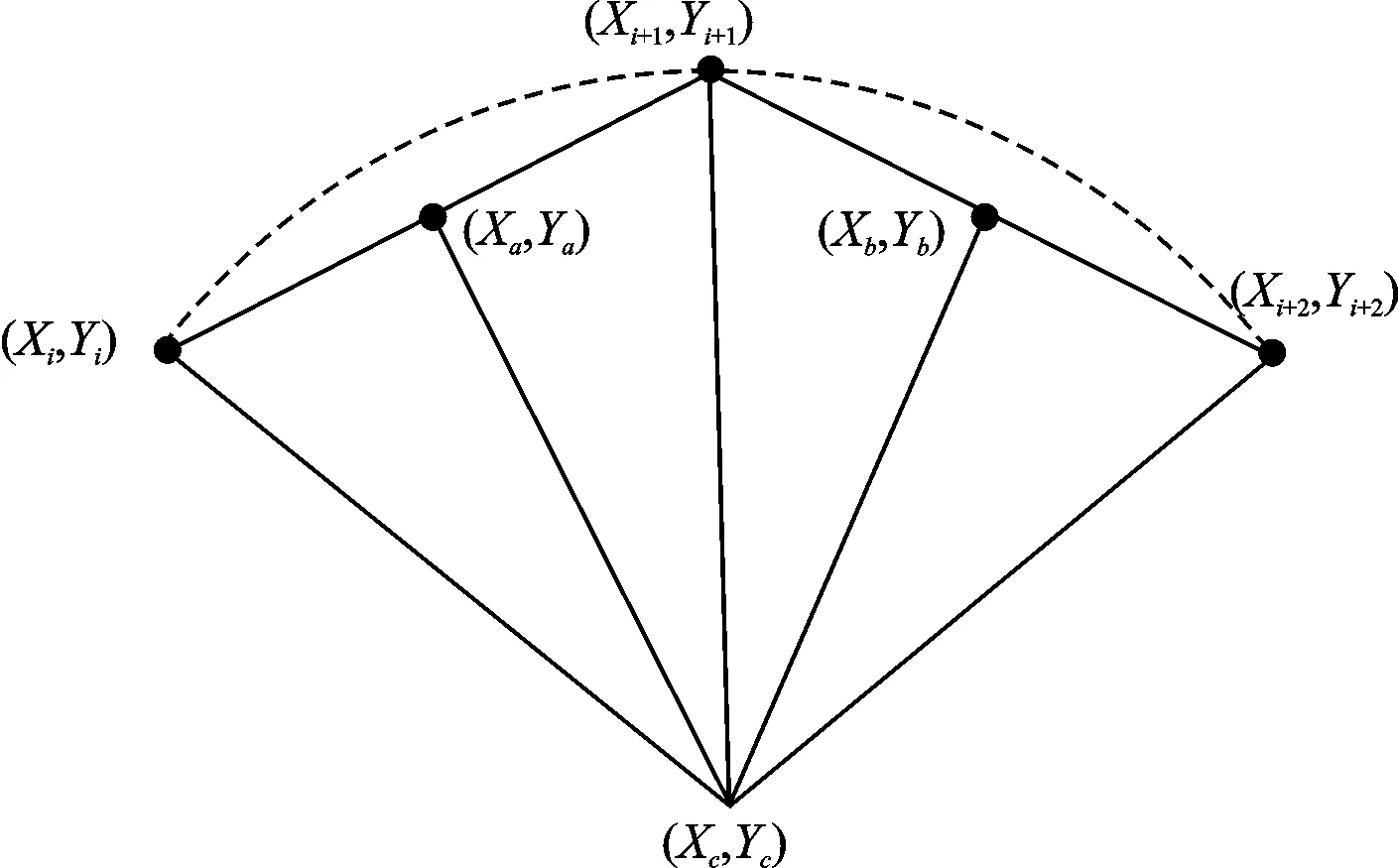
图4 三点定圆求圆半径推导示意图Fig.4 Derived schematic diagram of solution of the circle radius of three-point circle

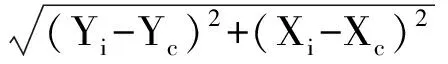
其中：

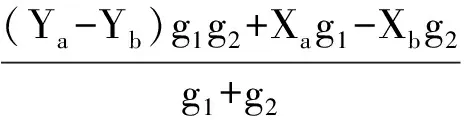
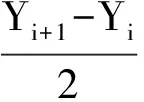
等跨度取圆弧计算比较半径后可以得到一段曲率半径最小点所在的圆弧,对所得小圆弧上进行拉格朗日多项式插值(插入10个点),对插入的点(连同小圆弧端点)进行下一轮三点定圆比较圆半径并找到曲率最大的一段圆弧(由3个插值点构成),取该圆弧的中间点输出即为所求e-lgp曲线的曲率最大点,进一步可以根据插值函数求出该点处切线斜率。该部分确定e-lgp曲线的曲率最大点可以在MATLAB中实现。

2.2 先期固结压力pc的确定

卡萨格兰德经典图解法(图5),作图步骤如下：

(3) B点对应的应力就是先期固结压力pc。

图5 卡萨格兰德经典图解法Fig.5 Classic graphic method of Casagrande

2.3 基于MATLAB和EXCEL结合的软件平台实现先期固结压力求解和自动作图

(1) 从EXCEL加载项扩展应用中安装MATLAB应用加载项,从EXCEL中启动MATLAB,成功实现MATLAB从EXCEL对应的单元中自动读取数据,并运用这些数据完成相应计算,将计算结果自动输送到EXCEL预先设定功能应用的单元格中。

(2) MATLAB中的M函数是通过相互嵌套调用实现求解e-lgp曲线的最大曲率点和该点切线斜率,并输出到EXCEL的功能单元格。MATLAB软件算法由前节先期固结压力求解部分可得。

(3) 在EXCEL中运用VBA宏汇编设计前期固结试验数据的统计和自动画出卡萨格兰德经典图解示意图的应用模版。VBA宏汇编设定好该EXCEL自动数据统计和绘图模版特定功能格的函数定义,当MATLAB中完成相应运算后将结果输回EXCEL时,单元格预设功能函数在启动按钮的激发下,自动完成作图。

3 计算实例

结合南阳膨胀土室内固结试验成果,分别利用计算机方法及传统卡萨格兰德经验作图法求解膨胀土先期固结压力,其物理力学指标及计算成果见表1,软件自动计算结果见图6。

由表1试验成果可知,不同深度土样皆为超固结状态,膨胀土因其特殊的工程性质,大都具有多裂隙性和超固结性,因此,结论符合实际情况。同时,由计算机计算得到的先期固结压力值与传统卡萨格兰德经验作图法非常接近,这说明本文采用计算机求解先期固结压力的方法是可行的。

4 结语

本文在对国内外各学者计算方法的研究基础上,通过Matlab语言编制了相应的计算程序,结合算例表明该方法对试验数据具有较好的适应性,且操作简便,能以图形化方式显示确定先期固结压力,避免人为误差,计算速度快,可以把该研究成果拓展到其他需要做大量数据统计、图形绘制和分析的应用领域中。但其计算精度依赖于计算理论和试验数据的准确性,所以,该方法有待进一步研究和试验数据的检验。

表1 试验区试样物理力学指标Table 1 Physical and mechanical indexes of sample in test area

图6 软件自动计算结果Fig.6 Automatic computation of software

[1] Matlock H S.Correlation for design of laterally loaded pile in soft clay[C]//Proceedings of 2nd Offshore Technology Conference.Houston:[s.n.],1970.

[2] 钱家欢，殷宗泽.土工原理与计算[M].北京：中国水利电力出版社,1996.

[3] 刘用海,朱向荣,常林越.基于Casagrande法数学分析确定先期固结压力[J].岩土力学,2009，1(1):211-214.

[4] 刘衍成.前期固结压力的计算和绘图程序[J].工程勘察,1987(3):10-15.

[5] 张书宪.用计算机绘图确定先期固结压力的一种方法[J].岩土工程界,2000,8(3):45-47.

[6] 周国云.一种确定前期固结压力(pc)的电算方法[J].水文地质工程地质,1987(5):34-36.

(责任编辑：陈文宝)

PENG Jing, ZHANG Shengjun, HE Jiao, JIANG Xiaojuan, ZHOU Huixian
(ChangjiangReconnaissanceTechnologyResearchInstitute,MinistryofWaterResources，Wuhan,Hubei430011)

Solving Pre-consolidation Pressure of Soil Based on Computer

On the basis of research the Casagrande’s experience graphic method,using the same span arc to find the circle radius and using Lagrange polynomial interpolation method to calculate the minimum curvature radius point,then using Matlab language to compile the corresponding calculation program to calculate the pre-consolidation pressure value.Combined with expansive soils examples show that the method has better adaptability to the test data,and easy to operate,and it also can be displayed graphically to determine pre-consolidation pressure,in the same time it can avoid human error,and have high computing speed,the research results can also be extended to other application areas which needs a lot of statistics,graphing,and analysis.

pre-consolidation pressure;Casagrande method;minimum curvature radius;MATLAB

2014-12-24改回日期：2015-03-02

彭静(1977-)，女，工程师，工程地质专业，从事岩土勘察试验工作。E-mail：tgsypj0104@sina.com

TU432

A

1671-1211(2015)02-0202-04

数字出版网址:http://www.cnki.net/kcms/detail/42.1736.X.20150204.1046.015.html 数字出版日期:2015-02-04 10:46