基于纤维模型的FRP约束混凝土圆柱本构模型研究
2015-06-16周芬冷举良杜运兴
周芬+冷举良+杜运兴

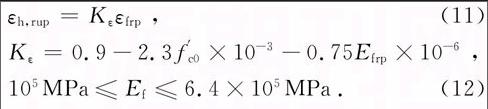
摘要:在OpenSees平台上采用纤维模型模拟FRP约束混凝土圆柱的受力性能时需要开发相应的本构模型.基于Jiang和Teng提出的分析型骨架本构模型,将不同峰值应力、应变计算公式的计算结果与试验结果进行比较,选择了更为精确的计算公式,并将其引入该骨架模型.该模型还考虑了箍筋对核心混凝土的约束作用,采用FRP极限环向抗拉应变折减系数得出FRP片材在环向受拉破坏时的极限拉应变.根据是否考虑钢筋的疲劳采用两种不同钢筋本构关系对试件进行模拟.采用该模型不但可以得到构件的轴向应力应变关系,还可以计算横向应变与轴向应力的关系,模拟结果与试验结果吻合较好.
关键词:纤维增强塑料;约束混凝土;纤维模型;本构模型
中图分类号:TB83;TM753 文献标识码:A
Research on the Constitutive Models of FRP
Confined Concrete Cylinder Based on Fiber Models
ZHOU Fen,LENG Ju-liang, DU Yun-xing
(College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China)
Abstract:The related constitutive model is needed when using fiber model to simulate the mechanical behavior of FRP confined concrete cylinder on OpenSees platform. Based on the skeleton-line constitutive model proposed by Jiang and Teng, the test results were compared with the calculation results under different peak stresses and strains, and more precise formulas were chosen and taken into the skeleton-line constitutive model. In the constitutive model, with the confinement effect of stirrup on core concrete taken into consideration, the ultimate tensile strain of FRP under hoop tensile failure was obtained by the reduction factors of ultimate hoop tensile strain. In addition, two different constitutive models were adopted to simulate the member according to whether considering the steel fatigue through the constitutive model. Both the relationship of axial stress and strain and the relationship of lateral strain and axial stress for the structural member were obtained, and the prediction results agreed well with the test results.
Key words:FRP(Fiber Reinforced Plastics);confined concrete;fiber models;constitutive models
OpenSees平台是基于纤维模型的计算平台,与传统的有限元相比,纤维模型能够在保证准确性的基础上大幅降低计算耗时,并且更易收敛,能够用于大型结构的数值模拟.国内学者在该平台上对构件、结构的仿真进行了广泛的研究,并积累了大量的科研成果[1-2].这些研究成果主要集中在钢筋混凝土结构及型钢混凝土结构领域.对于FRP加固的钢筋混凝土结构,OpenSees材料库中缺乏与其对应的本构模型,制约了该平台对这种结构的仿真分析.近年来,由于FRP材料优越的力学性能和物理性能,FRP片材已经广泛地用于加固结构和构件中,特别是震后结构的修复工作,FRP的约束作用不仅能提高结构的承载力,还能大幅提高柱在地震作用下的耗能能力和延性[3].因此,研究基于纤维模型的FRP约束混凝土柱的本构模型非常有意义.
目前,一些学者对基于纤维模型的FRP约束混凝土柱本构模型进行了初步研究,这些研究按模拟的方法可以分为3类:1)采用材料库中已有的材料,通过适当改变材料性能参数来模拟FRP约束混凝土材料.例如王代玉[4]采用预定义材料Concrete02,通过提高混凝土的极限抗压强度和极限压应变来模拟FRP约束混凝土,这样做的优点在于方便易行,不需要对OpenSees进行二次开发就能近似地模拟FRP约束混凝土的性能.但是由于材料Concrete02是基于钢筋混凝土构件提出的本构关系,用来模拟FRP约束混凝土是不够准确的,并且也不能考虑不同FRP材料性能参数对FRP约束混凝土构件的影响.2)采用简化了的FRP约束混凝土材料的本构模型,再将其嵌入OpenSees中.如何铭华等[5],虽然材料骨架曲线采用Lam等[6]提出的较为精确的FRP约束混凝土设计型本构模型,但是加卸载曲线却采用Karsan等[7]根据混凝土循环轴压试验提出的本构模型,这样虽然降低了编程难度,但也导致模拟结果不够精确.3)Teng等[8]采用C++编程,材料本构关系采用Teng等[9]提出的改进的设计模型,结合Lam 和Teng[10]提出的加卸载模型,并运用动态链接库建立新编材料与OpenSees平台的连接,成功模拟了一钢筋混凝土柱在水平往复荷载作用下的滞回性能,虽然模拟结果与试验有较好的吻合,但是该模型没有模拟出由于钢筋疲劳导致的骨架曲线的下降段,并且模拟结果的极限水平位移较试验结果小,说明其结果并不理想.
综上所述,可以看到:上述对FRP约束混凝土柱的研究采用的本构模型都是设计型本构模型,该类模型虽然简单易用,但是用于有限元数值模拟方面却不如分析型模型精确.为准确模拟FRP约束混凝土圆柱的受力性能,本文建立了适于运用到纤维模型中的单轴分析型本构模型,并进行了相应的程序模块开发.
1材料本构模型
1.1混凝土本构模型
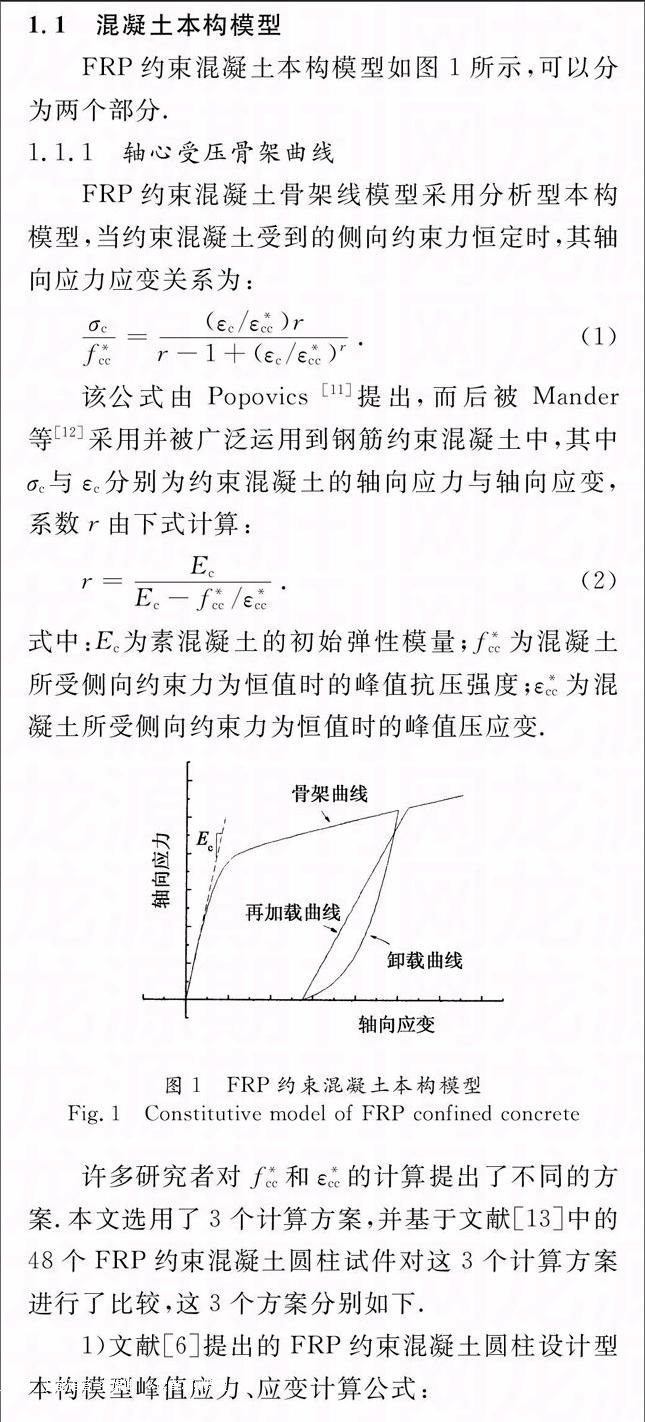
FRP约束混凝土本构模型如图1所示,可以分为两个部分.
1.1.1轴心受压骨架曲线
FRP约束混凝土骨架线模型采用分析型本构模型,当约束混凝土受到的侧向约束力恒定时,其轴向应力应变关系为:
σcf*cc=(εc/ε*cc)rr-1+(εc/ε*cc)r.(1)
该公式由Popovics [11]提出,而后被Mander等[12] 采用并被广泛运用到钢筋约束混凝土中,其中σc与εc分别为约束混凝土的轴向应力与轴向应变,系数r由下式计算:
r=EcEc-f*cc/ε*cc. (2)
式中:Ec为素混凝土的初始弹性模量;f*cc为混凝土所受侧向约束力为恒值时的峰值抗压强度;ε*cc为混凝土所受侧向约束力为恒值时的峰值压应变.
许多研究者对f*cc和ε*cc的计算提出了不同的方案.本文选用了3个计算方案,并基于文献[13]中的48个FRP约束混凝土圆柱试件对这3个计算方案进行了比较,这3个方案分别如下.
1)文献[6]提出的FRP约束混凝土圆柱设计型本构模型峰值应力、应变计算公式:
f*cc=f′c0+3.3fl, (3)
ε*ccεc0=1.75+12(flf′c0)(εlεc0)0.45.(4)
2)文献[13]提出的FRP约束混凝土圆柱分析型本构模型峰值应力、应变计算公式:
f*cc=f′c0+3.5fl, (5)
ε*ccεc0=1+17.5(flf′c0)1.2.(6)
3)文献[9]提出的FRP约束混凝土圆柱改进后的设计型本构模型峰值应力、应变计算公式:
f*cc=f′c0+3.5f′c0(2Efrptfrp(f′c0/εc0)D-0.01)εlεc0, (7)
ε*ccεc0=1.75+6.52Efrptfrp(f′c0/εc0)D0.8(εlεc0)1.45.(8)
式中:f′c0为素混凝土的抗压强度;εc0为素混凝土的峰值压应变;fl为混凝土受到的侧向约束力;εl为FRP材料的环向拉应变.
fl的计算公式为:
fl=-EfrptfrpεlR. (9)
式中:Efrp为FRP材料的弹性模量;tfrp为FRP片材的厚度;R为混凝土柱的截面半径.
公式(9)中的负号表示fl与εl方向相反,因为fl是混凝土受到的侧向压应力,而εl是FRP材料的环向拉应变.本文若无特别说明,假定压应变和压应力为正,而拉应变和拉应力为负.对于设计型本构模型而言,参数ε l等于FRP片材的极限环向拉应变εh,rup,而对于分析型本构模型而言,参数εl的计算应考虑整个受力过程中它的变化.本文采用的是分析型本构模型,采用文献[13]中的公式计算εl,该公式如下:
εcεc0=0.85(1+8flf′c0)×1+0.75(-εlεc0)0.7-
exp -7(-εlεc0). (10)
上述公式中,当已知轴向应变εc求解横向应变εl时需要采用迭代的方法进行计算.根据文献[13]中48个试件的试验资料,将以上3种方案的计算结果与试验结果进行对比分析,如表1所示.
表1中第2列与第4列表示不同方案对48个试件的峰值应力与应变的模拟结果与试验结果之比的平均值,可看到方案3对试件峰值应力的模拟最为精确,所以本文采用方案3的公式(7)计算试件的峰值应力.而对峰值应变的模拟,3个方案的模拟结果相差不大,本文采用相对简单的公式(6)进行模拟.
注:f*cct与ε*cct分别为试验试件峰值应力和应变.
1.1.2卸载、再加载曲线
国内外对FRP约束混凝土的轴心反复受压本构模型的研究已经较为成熟[14].本文的卸载和再加载曲线采用文献[10]提出的FRP约束混凝土圆柱的轴心受压卸载、再加载规则,由于该规则计算较为复杂,具体计算方法可参见文献[10].需要注意的是,由于该卸载、再加载规则是基于文献[6]中的设计型骨架本构模型建立的,所以当将其运用到本文的分析型骨架本构模型时,需要将它原本的峰值应力、应变计算公式改为本文的公式(7)和公式(6).
1.2钢筋本构模型
钢筋本构关系采用OpenSees材料库中的ReinforcingSteel材料模型,本构模型如图2所示.其中参数取值参照文献[15],初始强化点应变εsh取为屈服点对应应变的14倍 ,强化段初始弹性模量Esh取为2 138 MPa,极限强度fsu取1.5倍屈服强度fy,对应应变εsu取为εsh加上0.14.ReinforcingSteel相比于OpenSees中其他钢筋材料(如Steel01和Steel02),不仅更加适用于钢筋混凝土柱的非线性
分析[16],而且它还能考虑钢筋的强度退化、疲劳以及屈曲等问题.因此,本文采用材料ReinforcingSteel本构模型中预定义的Coffin-Manson[17]准则考虑钢筋的疲劳刚度退化问题对柱构件滞回性能的影响.
2试验分析与验证
本文采用OpenSees单元库中基于柔度法的梁柱单元nonlinearBeamColumn进行模拟.单元布置5个高斯积分点,混凝土圆柱纤维划分为沿径向和环向各为10,总共100个纤维,加载方式为位移控制加载.素混凝土初始弹性模量取为Ec=4 730(fc0) (MPa) [18],并且当素混凝土峰值点应变未知时取为0.002 2.由于采用纤维模型进行模拟,在建模过程中需要遵循以下假定:
1)不考虑试验中柱所受剪力作用;
2)不考虑钢筋的粘结滑移效应;
3)构件变形满足欧拉平截面假定.
2.1单调轴心受压试验
本文有11个FRP约束混凝土圆柱轴心受压试件,其中2个取自文献[13]中编号为28和29的试件数据,这两个试件全为FRP弱约束混凝土试件,另外9个都取自Xiao和Wu[19]的试验数据,这9个试件根据混凝土强度可分为3组,每组都包括3个试件,这3个试件分别包裹1~3层FRP片材.试件编号CL表示低强度混凝土,CM表示中等强度混
凝土,CH表示高强混凝土,F1到F3表示FPR层数从1~3层.试件几何材料属性如表2所示.Xiao等[19]的试件中没有给出FRP极限环向拉应变εh,rup的值,本文采用Lim等[20]提出的FRP极限环向抗拉应变折减系数Kε估算εh,rup的取值,具体公式如下:
εh,rup=Kεεfrp,(11)
Kε=0.9-2.3f′c0×10-3-0.75Efrp×10-6,
105MPa≤Ef≤6.4×105MPa.(12)
式中:εfrp为FRP轴心受拉极限应变;Efrp为FRP材料的弹性模量;f′co为素混凝土强度.
由于本文本构模型采用分析型模型,所以我们能够通过计算得到试件横向应变与轴向应变的关系,并且相比于文献[5]采用的设计型本构模型,本文还能模拟弱约束混凝土的强度下降段.在模拟试件28和29时,模型的FRP极限环向拉应变取为试件的平均值,由图3(a)我们可以看到本文对弱约束混凝土强度下降段的模拟较为准确.由图3(b),3(c)和3(d)可知:强度为33.86 MPa和43.77 MPa的混凝土试件的模拟结果与试验吻合良好,表明本文采用的纤维模型能够较好地模拟FRP约束混凝土材料的受力性能.而对于强度为55.21 MPa的混凝土试件的模拟,由于本文采用本构关系中的计算公式都是基于素混凝土强度不超过47 MPa的柱构件提出的,所以并不适用于素混凝土强度超过47 MPa的构件.需要注意的是图3中x轴表示混凝土材料应变,当其小于零时表示横向应变,当其大于零时表示轴向应变.
应变
(a)试件28-29
应变
(b)试件CLF1-CLF3
应变
(c)试件CMF1-CMF3
应变
(d)试件CHF1-CHF3
2.2水平循环加载试验
水平循环加载试验选用Haroun等 [21]中编号CS-R1的FRP约束混凝土圆柱进行模拟,试件高2 438 mm,直径610 mm,配置横向箍筋和纵向钢筋,其中横向箍筋直径为6.35 mm,间距为127 mm,屈服强度为210.3 MPa,纵向钢筋沿环向布置20根,每根钢筋直径为19.05 mm,屈服强度为299.2 MPa,混凝土保护层厚度为25.4 mm,混凝土和FRP片材材料属性如表3所示.
本文在建模过程中,考虑了横向箍筋对混凝土的约束作用.结合Mander等[12]和Carlo等 [22]提出的理论,采用下面公式计算混凝土受到的侧向约束力:
Pu=fl+flsAcc/Ag. (13)
式中:Pu为总约束力;fl为FRP提供的约束力,采用公式(9)计算;Acc为箍筋约束核心混凝土面积;Ag为整个柱截面面积;fls为横向箍筋提供的约束力,计算方法可以参见文献[12]和文献[22].根据试验条件,在建模过程中需要将构件底端设为固端约束,而顶端只约束其转动,并且需要施加大小为644.96 kN的轴力.
当采用ReinforcingSteel模拟钢筋且不考虑钢筋的疲劳及刚度退化时,计算结果如图4(a)所示,骨架曲线上水平力随着水平位移的增大而增加,并且几乎呈线性趋势,这明显与试验结果骨架曲线不符.试验骨架曲线中水平力在水平位移小于40 mm时,随着水平位移增大水平力也增大,但是位移继续增加以后,水平力的增大开始变缓,最后甚至出现下降段.同时模拟构件中滞回环也较试验过于饱满,整体来说模拟结果不太准确.
当考虑钢筋疲劳及刚度退化时(图4(b)),可以明显地看到其模拟结果滞回曲线与试验曲线吻合较好,并且能较好地模拟骨架曲线在水平位移较大时水平力的下降.将本文图4(b)得出的结果与文献[8]的模拟结果进行对比,结果如图4(c)所示,可以看到文献[8]模拟的滞回曲线没能模拟出FRP约束钢筋混凝土柱由于多次循环加载导致的水平承载力下降.同时文献[8]的滞回曲线中的极限水平位移较试验偏小,而本文由于考虑了FRP极限环向抗拉应变折减系数,所以可以精确估计构件的极限应变值,得出了与试验吻合较好的极限水平位移.需要注意的是,图4(b)模拟结果的滞回环较试验饱满,这主要是因为本文没有考虑钢筋与混凝土的粘结滑移因素,并且由于本文采用纤维模型进行模拟,也没有考虑剪力对滞回曲线的影响.
水平位移/mm
(a)不考虑钢筋疲劳结果与试验对比
水平位移/mm
(b)考虑钢筋疲劳结果与试验对比
水平位移/mm
(c)计算结果与文献[8]结果对比
3结论
1)本文基于OpenSees平台运用纤维模型对FRP约束混凝土圆柱进行了模拟分析,在Jiang和Teng提出的FRP约束混凝土圆柱的分析型骨架本构模型的基础上,通过对比不同本构模型的峰值应力、应变计算公式的模拟结果,选取了更为精确合理的计算公式,从而改进了FRP约束混凝土的骨架本构模型.在此基础上,结合Lam等提出的加卸载本构模型,本文通过C++编程成功地将FRP约束混凝土材料分析型本构模型嵌入OpenSees材料库中.
2)结合编制的C++程序,基于OpenSees平台采用纤维模型模拟了FRP约束混凝土圆柱不同受力状态下的应力应变结果,模拟结果不仅能得出构件轴向应变与轴向应力的关系,还得到构件横向应变与轴向应力的关系.需要注意的是,本文采用的本构模型只适用于素混凝土强度不高于47 MPa的构件.
3)本文在水平循环加载试验模拟过程中,考虑了箍筋对混凝土材料的约束作用,并且对纵向钢筋是否考虑钢筋的疲劳与刚度退化因素采用了两种钢筋本构模型,并对比了两者计算结果的滞回曲线.分析结果表明,不考虑钢筋疲劳与刚度退化时会夸大构件的刚度,导致过大估计构件的承载能力.当考虑钢筋疲劳与刚度退化时,模拟滞回曲线与试验吻合较好.
参考文献
[1]张传超,郑山锁,李磊,等. 基于柔度法的纤维梁柱单元及其参数分析[J].工业建筑,2010,40 (12):90-94.
ZHANG Chuan-chao, ZHENG Shan-suo, LI Lei,et al. Flexibility-based fiber beam-column element and its parametric analysis[J]. Industrial Construction, 2010, 40(12): 90-94. (In Chinese)
[2]韩军,李英民,姬淑艳. RC框架结构合理破坏机制的实现[J]. 哈尔滨工业大学学报,2010,42(12):2003-2008.
HAN Jun,LI Ying-min,JI Shu-yan. Realization of rational failure mechanism for the RC frame structure[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 2003-2008. (In Chinese)
[3]丁洪涛,易伟建,冼巧玲.碳纤维布(CFRP)加固压弯构件全过程分析[J].湖南大学学报:自然科学版,2003,30(3):139-141.
DING Hong-tao, YI Wei-jian, XIAN Qiao-ling. Nonlinear analysis of carbon fiber sheets (CFRP) strengthened members subjected to axial load and lateral shear[J]. Journal of Hunan University: Natural Sciences, 2003, 30(3): 139-141.(In Chinese)
[4]王代玉. FRP约束混凝土柱轴压本构关系及抗震性能[D].哈尔滨:哈尔滨工业大学土木工程学院,2008: 60-67.
WANG Dai-yu. Axial constitutive relationship and seismic performance of FRP confined column[D]. Harbin: School of Civil Engineering,Harbin Institute of Technology, 2008: 60-67.(In Chinese)
[5]何铭华,栾雨琪,刘晖,等.基于OpenSees的FRP约束混凝土本构开发及墩柱性能分析[J].桥梁建设, 2013, 43(6): 19-26.
HE Ming-hua, LUAN Yu-qi, LIU Hui, et al. Development of FRP confined concrete constitutive model and analysis of pier/column behavior based on OpenSees[J].Bridge Construction, 2013,43(6):19-26. (In Chinese)
[6]LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete[J]. Construction and Building Materials, 2003, 17(6/7): 471-489.
[7]KARSAN D, JIRSA J. Behavior of concrete under compressive loadings[J]. Journal of the Structural Division, ASCE, 1969, 95(12): 2543-2563.
[8]TENG J G, LU J Y, LAM L, et al. Numerical simulation of FRP-jacketed RC columns subjected to cyclic loading[C]// The 5th International Conference on FRP Composites in Civil Engineering. Beijing: Advances in FRP Composites in Civil Engineering, 2010:820-823.
[9]TENG J G, JIANG T, LAM L,et al. Refinement of a design-oriented stress-strain model for FRP-confined concrete[J]. Journal of Composites for Construction, 2009,13(4): 269-278.
[10]LAM L, TENG J G. Stress-strain model for FRP-confined concrete under cyclic axial compression[J]. Engineering Structures, 2009, 31(2): 308-321.
[11]POPOVICS S. Numerical approach to the complete stress-strain relation for concrete[J]. Cement and Concrete Research, 1973, 3(5): 583-599.
[12]MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.
[13]JIANG T, TENG J G. Analysis-oriented stress-strain models for FRP-confined concrete[J]. Engineering Structures, 2007, 29(11): 2968-2986.
[14]王代玉,王震宇,乔鑫.CFRP中等约束钢筋混凝土方柱反复受压本构模型[J]. 湖南大学学报:自然科学版,2014,41(4): 39-46.
WANG Dai-yu, WANG Zhen-yu, QIAO Xin. Cyclic stress-strain model for CFPR moderately-confined reinforced concrete square columns[J]. Journal of Hunan University: Natural Sciences, 2014, 41(4): 39-46.(In Chinese)
[15]DHAKAL R P, MAEKAWA K. Path-dependent cyclic stress-strain relationship of reinforcing bar including bucking[J]. Engineering Structures, 2002, 24(11): 1383-1396.
[16]HEO Yeong-ae, KUNNATH S K. Sensitivity to constitutive modeling in fiber-based discretization of reinforced concrete members for performance-based seismic evaluation[J]. Advances in Structural Engineering,2009, 12(1): 37-51.
[17]MAZZONI S, MCKENNA F, MICHAEL H S, et al. OpenSees users manual[R]. Berkeley, Califorma: PEER, University of Califorma,2004.
[18]ACI 318-95Building code requirements for structural concrete (318-95) and commentary (318R-95)[S]. Farmington Hills, Michigan, USA: American Concrete Institute (ACI), 1999.
[19]XIAO Y, WU H. Compressive behavior of concrete confined by carbon fiber composite jackets[J]. Journal of Materials in Civil Engineering, 2000, 12(2): 139-146.
[20]LIM J C, OZBAKKALOGLU T. Confinement model for FRP-confined high-strength concrete[J]. Journal of Composites for Construction, 2014,17(5):1-19.
[21]HAROUN M A,MOSALLAM A S,FENG M Q. Experimental investigation of seismic repair and retrofit of bridge columns by composite jackets[J]. Journal of Reinforced Plastics and Composites, 2003, 22(14): 1243-1268.
[22]CARLO P, CLAUDIO M. Analytical modelfor FRP confinement of concrete columns with and without internal steel reinforcement[J]. Journal of Composites for Construction, 2010, 14(6): 693-705.
