窄带干扰抑制对载波相位测量零值影响分析
2015-06-15刘泳庆安建平李一品
刘泳庆,安建平,李一品
(北京理工大学信息与电子学院,100081北京)
窄带干扰抑制对载波相位测量零值影响分析
刘泳庆,安建平,李一品
(北京理工大学信息与电子学院,100081北京)
为研究窄带干扰抑制对卫星导航系统载波相位测量零值的影响,采用典型窄带干扰抑制算法的等效滤波模型进行分析,构建窄带干扰抑制下的载波相位测量零值偏差分析模型,推导载波相位测量零值偏差与等效滤波器的关系,并给出载波相位测量零值无偏性的条件.分析表明:等效滤波器为线性相位滤波器的窄带干扰抑制算法对载波相位测量零值没有影响,等效滤波器为非线性相位滤波器的窄带干扰抑制算法对载波相位测量零值的影响与等效滤波器的时域抽头系数直接相关.蒙特卡洛仿真给出了典型窄带抑制干扰算法在不同窄带干扰参数下对载波相位测量零值造成的偏差.
载波相位测量零值;窄带干扰抑制;载波环;相频响应
载波相位测量在卫星导航系统精密定位中起到关键性作用[1-2],载波相位测量误差通常包括测量精度与测量零值.其中,测量精度是对载波相位随机误差的度量,其分析已经非常成熟,主要的误差来源包括相位抖动和动态应力误差;测量零值是对载波相位系统误差的度量,通常工程上对载波相位测量零值不太关注.然而在复杂多变的信息对抗信道环境中,窄带干扰抑制算法的应用在实现了系统对时变窄带干扰抑制的同时[3-5],对载波相位测量零值造成影响.在载波相位测量零值出现误差的情况下去分析其测量精度是舍本逐末的.
目前,国内外针对载波相位测量零值偏差的研究较少.载波相位测量零值偏差是指接收机对载波相位测量零值的影响,文献[6-7]通过将阵列处理传递函数的相频响应泰勒展开,并省略了二次项及高次项,得到载波相位测量零值偏差由泰勒展开式中的常数项决定、时间延迟偏差由泰勒展开式中一次项系数决定的结论;然而该分析方法不仅忽略了系统传递函数的幅频特性对载波相位测量零值的影响,并且忽略高阶展开项的近似方法会带来分析误差.文献[8]通过仿真手段分析了自适应阵列天线在进行空时域干扰抑制处理时对GNSS信号造成的码/载波相位偏差;但通过仿真分析的方法并不能从本质上给出消除或者补偿偏差的方法.文献[9]分析信道滤波器对接收机载波相位测量零值的影响,基于反正切鉴相器模型,推导了载波相位测量零值无偏差的充分必要条件,并给出信道滤波器在不同特性下载波相位测量零值偏差的表达式,但是该分析仅针对二次曲线型群时延特性的滤波器进行讨论,不能够全面涵盖窄带干扰抑制的等效滤波器特性.
本文以窄带干扰抑制后接收信号的载波相位测量零值为研究对象,基于锁相环对输入信号相位测量的无偏性构建载波相位测量零值分析模型,结合窄带干扰抑制的等效滤波模型进行理论分析,推导载波相位测量零值偏差的数学表达,并由此推出载波相位测量零值无偏的条件.最后通过蒙特卡洛仿真验证时域自适应滤波的等效滤波器为线性相位、时域自适应滤波的等效滤波器为非线性相位以及频域陷波技术3种情况下的载波相位测量零值偏差.
1 载波相位测量零值分析模型
载波同步的任务是在接收端产生出与接收信号载波频率、相位都一致的本振信号,从而完成载波的完全剥离[10].这里假设伪码同步是理想的,即复制的伪码与接收信号的伪码相位完全一致.载波相位估计是通过锁相环实现的,其典型实现结构见图1.无论锁相环的阶数为一阶或是多阶,锁相环误差信号的稳态终值均为零,也就是说,任何阶数的锁相环都可以准确无误地跟踪、锁定输入信号的相位零值.
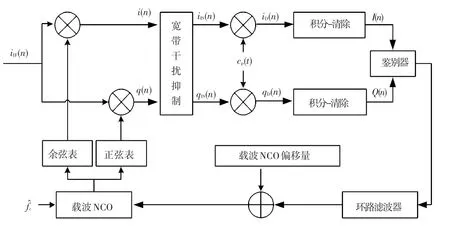
图1 载波相位估计器实现结构
假设rIF(n)为中频采样接收信号,w(n)为零均值高斯白噪声,j(n)为窄带干扰信号,sIF(n)为发送扩频信号,D(n)为发送数据比特,通常采用双极性表示{±1},c(n)为伪码序列,fc为记到达接收端的信号载波频率,θ0为相位,Ts为采样间隔:
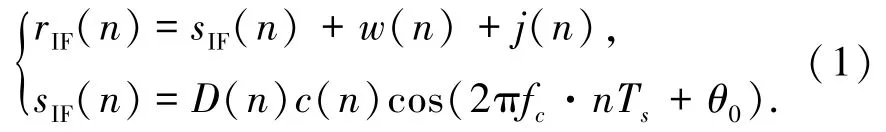
显然载波相位测量零值与噪声项无关,因此在分析中忽略白噪声项[4].记^fc为载波频率估计值,^θ0为载波相位估计值,也就是载波相位测量零值.正交下变频完成载波的剥离:
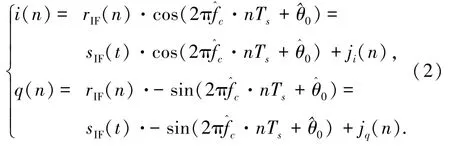
Δf=fc-^fc为频率估计误差;Δθ=θ0-^θ0为相位估计误差,也就是载波相位测量零值偏差.本文讨论载波相位测量零值问题,因此假设载波频率估计误差为0,即Δf=0.则式(2)化简为
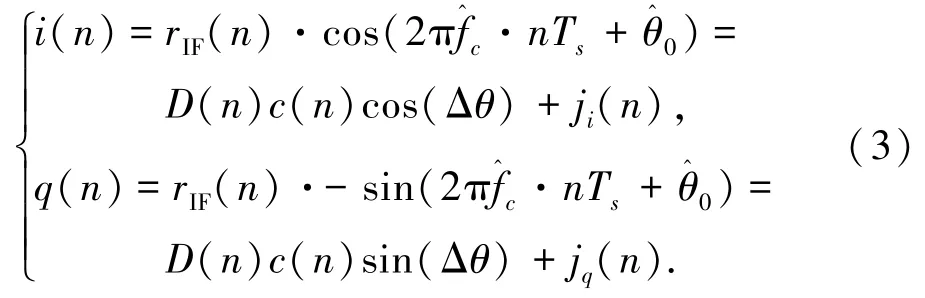
记干扰抑制滤波器为h(n),干扰抑制后的基带信号可为

在理想伪码同步情况下有

记相干积分时间为T0,则L=T0/Ts为相干积分时间内的采样点数,相干积分后的信号为

最后通过相位鉴别器得到载波相位测量零值偏差的估计
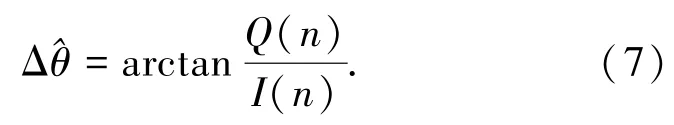
载波相位测量零值偏差包括测量的固定偏差和随机偏差,其中固定偏差表示由于信号处理带来的固有偏差,如由于滤波对接收信号造成时延从而带来的固定偏差,这部分偏差不随外部环境变化,可通过补偿的方式消除影响;随机偏差表示由于外部环境变化而导致系统产生的随机误差,如由于干扰频率、干扰功率或干扰带宽等特性发生变化导致窄带干扰抑制模块的特性发生变化,从而引起载波相位测量零值发生变化,该误差是影响载波相位测量零值性能的主要因素.
2 窄带干扰抑制模型
如图1所示,窄带干扰抑制模块作为接收链路中的一个插入模块,可以等效为一个数字滤波器.记F[]为信号的频域变换,滤波器的频率响应表述为

数字滤波器按照相频响应是否为频率的线性函数可分为线性相位滤波器和非线性相位滤波器.其中,线性相位滤波器由于不会造成信号的相位失真而被广泛应用.线性相位滤波器满足共轭对称或共轭反对称的时域特性[11].记滤波器脉冲响应为h(n),滤波器阶数为N,则线性相位滤波器满足下式
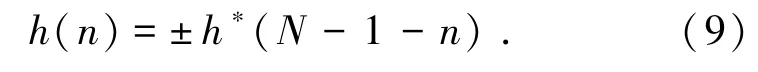
其实部和虚部满足:

常见的窄带干扰抑制手段包括时域自适应滤波技术和频域陷波技术[12].
频域陷波技术利用窄带干扰与扩频信号在频率域能量聚集度的差别,以接收信号频谱幅度统计量的线性组合作为门限来检测并抑制干扰.其典型结构框图见图2.
频域陷波技术等效滤波器hfde的频率响应:
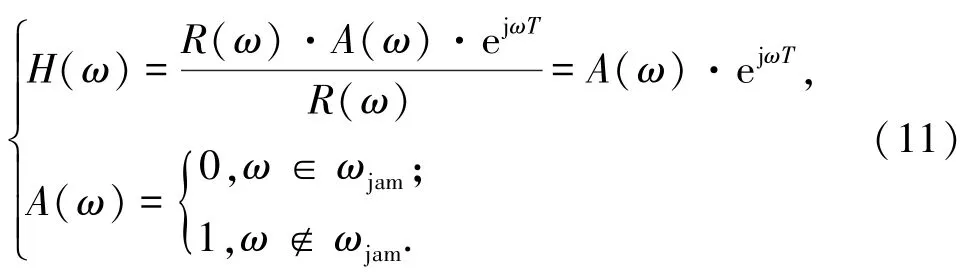
式中:A(ω)为干扰删除图样,ωjam为干扰所占频率集合;T为系统时延,取决于FFT的点数、FFT的计算方法和干扰抑制造成的延迟.可见,频域陷波技术的等效滤波器hfde可看作一个线性相位的带阻滤波器.

图2 频域陷波技术实现结构
3 窄带干扰抑制下的载波相位测量零值分析
3.1 线性相位滤波器
等效滤波器为线性相位的窄带干扰抑制算法对信号不会造成相位失真.记滤波器时域为
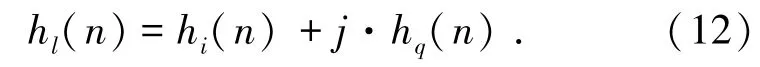
代入式(3)、(4),可得干扰抑制后的基带信号:
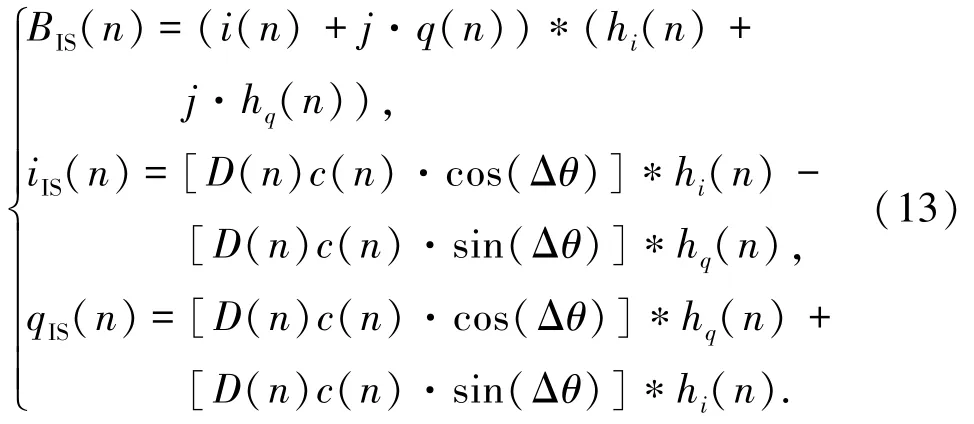
在理想伪码同步情况下cp(n)=c(n),可实现对伪码的完全剥离,因此结合式(5)(13)可得
筹资活动现金流对企业的发展具有辅助作用,无论是在企业亟需解决资金问题时还是扩大投资时,有效的筹资行为都可以对企业的发展起到至关重要的作用。因此,企业应当建立稳定的筹资渠道,确保企业经营稳定性。
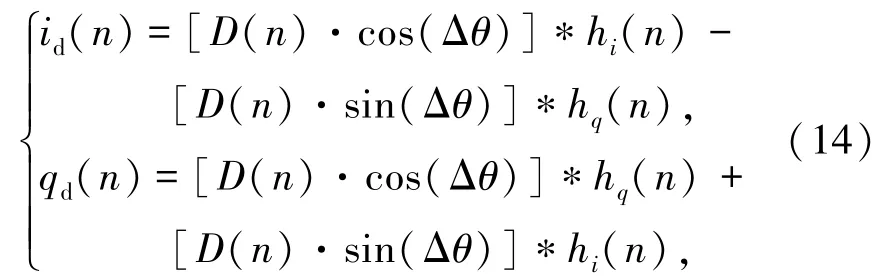
记:
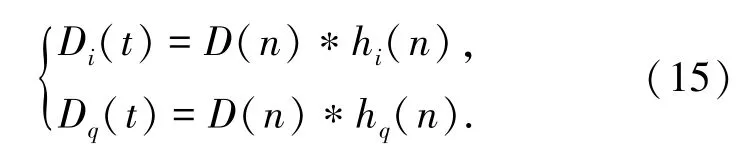
于是式(14)可表达为

代入相干积分表达式(6),可得
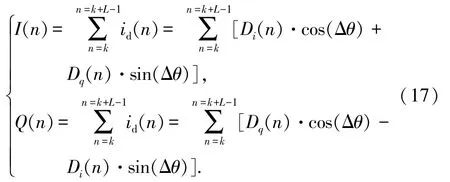
D(n)为发送数据比特.在卫星导航系统中由于采用了扩频的体制,因此码速率远大于信息速率,再结合奈奎斯特采样定理可知,信号采样速率同样远大于信息速率.因此,可认为D(n)在相干时间T0内保持数据电平不变,为1或-1.
结合式(10)、(15),可知,当线性相位滤波器满足共轭对称特性时有

将式(18)代入式(17),可得输入鉴相器的相干积分结果表达:
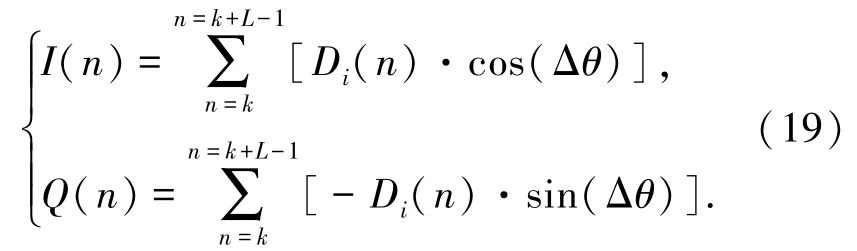
最后通过相位鉴别器得到载波相位测量零值偏差的估计:

当线性相位滤波器满足共轭反对称特性时有
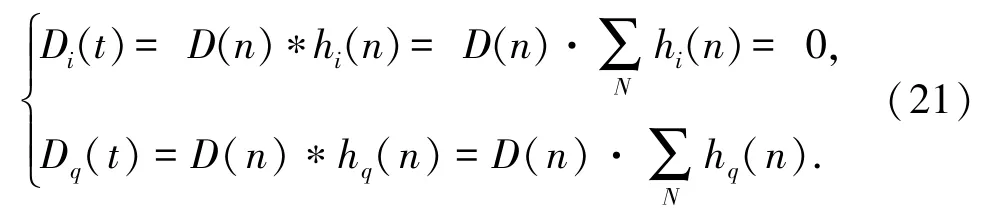
将式(21)代入式(17),可得输入鉴相器的相干积分结果表达:

最后通过相位鉴别器得到载波相位测量零值误差的估计:
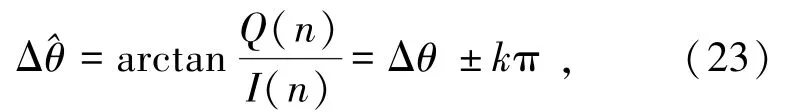
当锁相环环路达到稳态时,有[13]

于是Δθ=±k·πor±k·π/2,即载波相位测量零值的估计会出现π或π/2的固定偏差.可看出,该固定偏差与干扰位置、干扰强度等干扰参数无关.因此,在不同窄带干扰环境中,窄带干扰抑制等效的线性相位数字滤波器仅造成载波相位测量零值出现固定偏差而没有随机偏差.
3.2 非线性相位滤波器
非线性相位的数字滤波器会对信号造成相位失真.结合式(14)、(16)可得
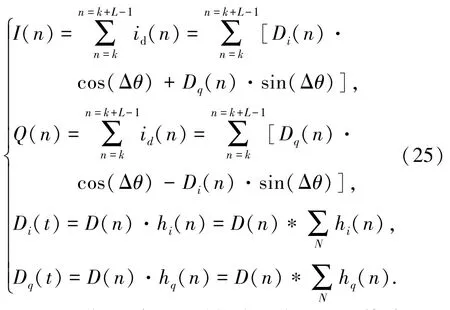
通过相位鉴别器得到载波相位误差的估计:

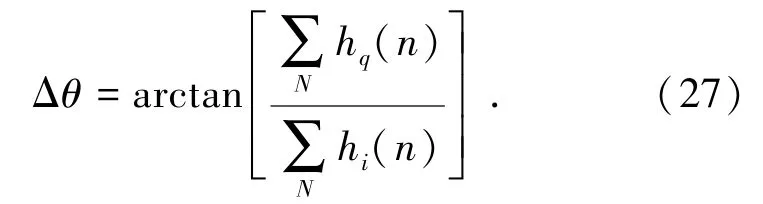
因此,满足载波相位测量零值无随机偏差的条件是Δθ为固定常数,即在不同的干扰环境中,自适应窄带干扰抑制算法的等效滤波器的虚部之和与实部之和的比值为固定常数是满足载波相位测量零值无随机偏差的充分必要条件.显然,线性相位滤波器是其中一个特殊情况.
根据以上两节,在设计卫星导航接收机的窄带干扰抑制算法时应尽量采用等效滤波器为线性相位的窄带干扰抑制算法以保证载波相位测量零值的无偏性;如果在特殊场合必须采用等效滤波器为非线性相位的窄带干扰抑制算法,则可以根据式(27)对载波相位测量零值进行实时补偿.
4 仿真分析
针对典型窄带干扰抑制算法进行仿真.仿真模型基于图1.载波相位鉴别器采用反正切相位鉴别器,信息速率50 bps,码速率为1.023 Mcps,采样速率为8 MHz,积分时间取1 ms,仿真时间10 s.由于载波相位测量零值的固定偏差对性能并无影响,因此仿真结果给出的是载波相位测量零值的随机偏差.
4.1 时域自适应滤波的等效滤波器为线性相位滤波器
采用基于LMS的自适应滤波算法,滤波器采用双边带滤波器[14],抽头系数更新满足式(8)共轭对称特性.滤波器阶数选择20阶,在不同干扰位置、不同干扰强度和不同干扰带宽的环境下得到不同陷波位置、不同陷波深度和不同陷波带宽的线性相位滤波器,基于收敛的滤波器权值进行载波相位测量零值的仿真分析.仿真结果见表1.
载波相位测量零值偏差在不同陷波位置、不同陷波深度和不同陷波带宽的线性相位滤波器下,仿真结果<10-12,该数值是仿真中的计算误差.仿真结果表明:不同陷波位置、不同陷波深度和不同陷波带宽的线性相位滤波器,对于载波相位测量零值是不会造成随机偏差的.
4.2 频域陷波技术
采用基于CME算法[15]的频域陷波技术进行窄带干扰抑制.针对不同干扰位置和不同干扰带宽的环境下进行频域抗干扰处理,进行载波相位测量零值的仿真分析.仿真结果见表2.

表1 线性相位的时域自适应滤波下的载波测量零值偏差

表2 频域陷波技术下的载波测量零值偏差
载波相位测量零值偏差在不同陷波位置和不同陷波带宽的频域陷波技术下,仿真结果<10-15,该数值是仿真中的计算误差.这是因为在Matlab仿真软件中,数值存在默认的精度,该精度可以用函数eps进行测定,例如eps(1)=2.220 4×10-16.随着数值运算的增加,误差一定会呈现增大的趋势.
仿真结果表明:针对不同干扰位置和不同干扰带宽环境下的自适应频域陷波技术对载波相位测量零值不造成随机偏差.
4.3 时域自适应滤波的等效滤波器为非线性相位滤波器
同4.1节,采用基于LMS的自适应滤波算法,滤波器采用双边带滤波器,但是抽头系数更新时不约束线性相位特性,即不需要满足共轭对称特性.滤波器阶数选择18阶,在不同干扰位置、不同干扰强度和不同干扰带宽的环境下得到不同陷波位置、不同陷波深度和不同陷波带宽的非线性相位滤波器,基于收敛的滤波器权值进行载波相位测量零值的仿真分析.仿真结果见表3.
仿真结果表明:不同陷波位置、不同陷波深度和不同陷波带宽的非线性相位滤波器,对于载波相位测量测量零值是有偏的;并且仿真结果与理论推导结果式(27)吻合.在采用等效滤波器为非线性相位的窄带干扰抑制算法时,根据式(27)对载波相位测量零值可以进行有效的实时补偿.

表3 非线性相位的时域自适应滤波下的载波测量零值偏差
5 结 语
本文针对窄带干扰抑制下的载波相位测量零值偏差进行分析,研究结果表明:等效滤波器为线性相位滤波器的窄带干扰抑制算法对载波相位测量零值没有影响,等效滤波器为非线性相位滤波器的窄带干扰抑制算法对载波相位测量零值的影响与等效滤波器的时域抽头系数直接相关,满足式(27).卫星导航接收机的窄带干扰抑制算法设计应尽量采用线性相位滤波,以保证载波相位测量零值的无偏性;非线性相位滤波器具有阶数小、陷波性能好等优点,在采用等效滤波器为非线性相位的窄带干扰抑制算法时,可以根据式(27)对载波相位测量零值进行实时补偿.如何针对非时域的窄带干扰抑制技术推导其等效滤波器模型并针对载波相位测量零值误差进行补偿还需进一步研究.
[1]HATCH R R,SHARPE R T,YANG Yunchun.An innovative algorithm for carrier-phase navigation[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation.Long Beach,CA:Institute of Navigation(ION),2004:1431-1437..
[2]隋叶叶,杨小江,柳涛.载波相位平滑伪距算法研究与精度分析[J].电子设计工程,2013,21(8):112-115.
[3]PING Lai,LU Ruimin.An improved variable step-size affine projection algorithm for narrowband interference suppression in DSSS systems[C]//2013 International Conference on Quality,Reliability,Risk,Maintenance,and Safety Engineering(QR2MSE).Chengdu:IEEE,2013:2043-2046.
[4]HAKAM A,SHUBAIR R,JIMA S,et al.Robust interference suppression using a new LMS based adaptive beamforming algorithm[C]//Mediterranean Electrotechnical Conference.Beirut:IEEE,2014:45-48.
[5]MEI Lin,ZHANG Qinyu,SHA Xuejun,et al.WFRFT precoding for narrowband interference suppression in DFT-based block transmission systems[J].IEEE Communications Letters,2013,17(10):1916-1919.
[6]FANTE R L.Performancemeasures for GPS anti-jam antenna arrays[R].Massachusetts:The MITRECorporation,2006.[7]CHURCH C M.Estimation of adaptive antenna induced phase biases in global navigation satellite systems receiver measurements[D].Ohio:The Ohio State University,2009.
[8]赵宏伟,冯娟,廉保旺.GNSS自适应阵列天线引入误差的分析与估算[J].系统工程与电子技术,2014,36(8):1460-1465.
[9]李柏渝.高性能卫星导航接收机模拟信道关键技术研究[D].长沙:国防科学技术大学,2011.
[10]李柏渝,陈雷,李彩华,等.通道非理想特性对导航接收机伪码测距零值的影响分析[J].电子与信息学报,2011,33(9):2138-2143.
[11]PROAKIS JOHN G,MANOLAKIS DIMITRIS G.Digital signal processing:principles,algorithms,and applications,3rd edition[M].Englewood Cliffs:Prentice Hall,1998.
[12]MILSTEIN L B.Interference rejection techniques in spread spectrum communications[J].Proceedings of the IEEE,1988,76(6):657-671.
[13]GARDNER FLOYDM.Phaselock techniques,third edition[M].New York:Wiley-Interscience,2005.
[14]LOH-MING LI,MILSTEIN L B.Rejection of narrowband interference in PN spread-spectrum systems using transversal filters[J].IEEE Transactions on Communications,1982,30(5):925-928.
[15]HENTTU P,AROMAA S.Consecutive mean excision algorithm[J].Proceedings of the IEEE International Symposium on Spread Spectrum Techniques and Application,Prague,Czech Republic,2002,2(2):450-454.
(编辑苗秀芝)
Effect of narrowband interference suppression on carrier phase biasesmeasurements
LIU Yongqing,AN Jianping,LIYipin
(School of Information and Electronics,Beijing Institute of Technology,100081 Beijing,China)
To explore the effect of narrowband interference suppression on carrier phasemeasurement zero value for satellite navigation system,this article establishes the equivalent filtermodel for classic NBIsuppression algorithm,and presents a study in order to analyze the effect of NBIsuppression on Carrier Phase bias.Then,the articlebuilds an analysismodel of carrier phase zero value in the introduction of the NBIsuppression,works out the relationship between the carrier phase zero value bias and equivalent filter,and shows a condition for the unbiasedness of carrier phasemeasurement zero value.It is shown that linear phase filter has no effect on carrier phase zero value. Nonlinear phase filter has an effect on carrier phase zero value,which isdirectlyrelatedtothefilter weights.Based on the Monte Carlosimulation,thebiasvalue of carrier phase measurement zero value,which is simulated in the different parameter of the narrowband interference by using classic narrowband interference suppression algorithms,is obtained.
carrier phase zero value;narrowband interference suppression;carrier loop;phase-frequency response
TN914.42
:A
:0367-6234(2015)11-0102-06
10.11918/j.issn.0367-6234.2015.11.018
2014-09-22.
国家自然科学基金(61271258,61301089).
刘泳庆(1987—),男,博士研究生;安建平(1965—),男,教授,博士生导师.
安建平,an@bit.edu.cn.
