多特征结合相似度优化的三维工程模型检索算法

庄廷，张旭堂，侯珍秀

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

多特征结合相似度优化的三维工程模型检索算法

庄廷，张旭堂，侯珍秀

（哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

为提高三维模型的检索准确度，针对工程三角网格模型提出了一种基于随机点间距离和法向夹角余弦联合分布及二进制粒子群优化的检索算法。在模型表面构造若干随机点并计算各点之间的距离和法向夹角余弦，然后以距离和余弦为坐标轴建立距离－余弦二维网格，统计各网格中的随机点数量，得到三维模型的距离⁃余弦联合形状分布矩阵，用分布矩阵之间的L2距离表示模型之间的相似度。为了体现形状分布矩阵中各元素对模型相似度影响的差异性，采用一种基于二进制粒子群优化的方法对相似度计算过程进行了改进。实验结果表明，本算法可有效提高工程三角网格模型检索的准确性。

三维模型检索；基于内容的检索；多特征联合；距离⁃余弦分布；相似度计算；二进制PSO优化

随着三维模型在机械行业的广泛使用，如何有效地重用三维模型逐渐引起了学术界和工业界的重视，作为模型重用首要环节的模型检索问题更是成为研究热点［1⁃3］，这也是本文的研究目的所在。三维模型检索研究中，基于模型内容的检索技术由于其良好的检索性能受到了广泛关注。基于内容的检索算法分为3个步骤，首先对模型进行归一化处理，消除模型外形大小和位姿对模型检索造成的影响；然后自动计算并提取三维模型的特征，如形状、空间关系等，建立三维模型的多维信息索引；最后以多维特征空间中特征向量之间的距离表示模型之间的相似度［4］。文献［5］提出的基于形状分布的三维模型检索算法（D2）是基于内容的三维模型检索领域的开创性算法。该算法首先在模型表面构造随机点，然后计算任意2个随机点之间的欧式距离，根据距离的分布情况构造距离分布直方图。使用两个直方图之间的距离表示模型之间的相似度。D2算法无需归一化处理，实现简单、计算快捷。但由于仅使用随机点之间的距离作为形状特征，所以对模型的分辨能力有限，对复杂模型的检索效果不佳。为了弥补D2算法的不足，有学者对其进行了改进［6⁃9］。这些改进算法通过改善D2的特征提取环节不同程度地提高了D2的检索能力，但都忽视了对相似度计算环节的改善。为此，本文从以下两方面入手提出了一种新的检索算法：1）使用随机点距离－弦联合分布，通过多特征联合增强算法检索能力；2）以检索结果最优为目标，采用二进制粒子群算法对距离⁃余弦联合分布矩阵各行进行筛选，用选中的行进行相似度计算。

1 算法说明

1.1 基于距离－向夹角余弦分布的模型

1.1.1 距离与法向夹角余弦的计算

本文采用文献［5］的随机点构造方法，随机点的法向与其对应的三角面片法向一致。图1中的P1和P2表示2个随机点，n1和n2为2个随机点对应的法向，d表示P1和P2之间的欧式距离，α为n1和n2的夹角。

图1 随机点之间的距离与法向夹角示意图Fig.1 The distance and included angle of two random points

1.1.2 距离⁃余弦二维分布矩阵

设随机点间距离的最大值为dmax，平均值为davg。以距离作为横轴，余弦作为纵轴，将（0，1）、（dmax，1）、（dmax，－1）和（0，－1）4个点确定的矩形区域划分成一个m×n网格，用bij（i＝1，2，..，m；j＝1，2，..，n）表示单元网格。对距离进行平均值归一化，将［0，davg］和［davg，dmax］分别等分为n／2个单元；余弦的值域为［－1，1］，等分为m个单元。如果随机点之间的距离属于横轴单元j，夹角余弦属于纵轴单元i，网格bij中的数字加1。当所有随机点对统计完毕后，使用网格中的数字组成一个m×n矩阵，称该矩阵为模型的距离⁃余弦分布矩阵（下文将其简称为DC分布）。表1为2个模型的D2分布和DC分布的比较，这2个模型外形迥异，但D2分布较为相似，DC分布则明显不同。由此可见DC分布对模型的分辨能力强于D2。

表1 距离－余弦联合形状分布示例Table 1 Examples of distance⁃cosine distribution

1.2 基于二进制粒子群优化的相似度计算过程

1.2.1 相似度计算公式改进

得到模型的DC分布矩阵后，模型相似度计算问题转化为分布矩阵之间的距离计算问题。本文使用DC矩阵之间的L2距离来表示模型之间的相似度。令A、B分别代表模型ma和mb的DC分布矩阵，aij和bij表示A、B的元素，模型ma和mb之间的相似度计算公式如下

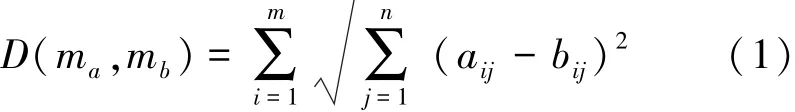
为了消除分布矩阵中噪音数据对相似度计算带来的影响，对式（1）进行了修改，加入系数向量X。X＝｛x1x2..xn｝′，其中xi等于1或0。式（2）为改进后的相似度计算公式。当xi＝0时，分布矩阵的第i行将不参与相似度计算。当X不全为1时，与式（1）相比，式（2）的计算结果将发生变化，即ma和mb的相似度发生变化。

如果使用ma表示检索模型，mb表示模型库中的模型。使用式（1）计算模型库中所有模型与ma的相似度，按照与ma的相似度从小到大的顺序对模型库中的所有模型进行排序，排序结果称为相似度排名（或者检索结果）。当前通用的检索算法性能评价指标均以相似度排名为依据对检索算法的性能做出定量评价，相似度排名的评价越高说明检索算法性能越强，反之则越差。由式（2）知，对同一个检索模型，采用不同的X可产生不同的相似度排名，使用算法性能评价指标对这些排名进行分析，结果必然有优有劣。由此可知，X的变化可以影响到算法的检索性能。对X的变化加以控制，保证其变化始终朝着相似度排名更优（算法性能评价更优）的方向进行，这就是本文相似度计算环节的优化思路。

1.2.2 二进制粒子群优化

粒子群优化算法（particle swarm optimization，PSO）是由Kennedy等提出的一种非线性优化算法［10］。PSO求解优化问题时首先随机生成若干个粒子，每个粒子对应搜索空间中的一个解。粒子本身有2个属性：位置和速度，还有一个由被优化函数决定的适应度，适应度描述了粒子对优化问题的优劣程度。粒子的初始状态随机确定后，算法进入迭代求解过程。在每一次迭代中，粒子通过跟踪2个“极值”来更新自己的速度和位置信息：一个是该粒子当前的历史最优解，称为个体极值点（用gbest表示），另一个是整个种群的当前最优解，称为全局极值点（用gbest表示）。每次迭代结束后，粒子根据适应度的大小更新自己的个体极值点gbest，并在所有的gbest中选出最优解作为种群的全局极值点gbest。迭代终止条件为预先确定的最大迭代次数或者为对优化结果的精度要求。为了解决组合优化问题，Kennedy等在PSO的基础上提出了二进制离散版本的PSO算法［11］，其优化思想与PSO一致。二进制PSO算法在第k次迭代时，粒子Pm按照

更新自己的速度和位置信息。式中：vmn和xmn分别为粒子Pm在第k次迭代中第n维的速度和位置；pbestmn表示粒子Pm在第k次迭代后得到的个体极值点在第n维的位置，gbestn表示在第k次迭代后得到的全局极值点第n维的位置；w为惯性权值；c1和c2为学习因子；rand1、rand2以及是属于（0，1）的随机数；

1.2.3 粒子适应度函数

理论上讲，所有相似度排名的评价指标均可作为粒子适应度函数。但是，由于在实际使用中只能将检索结果中排在前几位的模型返回给用户（如前10个模型），所以在排名靠前的检索结果中相关模型越多，排名越靠前，算法的实用性越强。为此，本文选用相似度排名评价指标First⁃Tier（下文用FT表示）［12］作为二进制PSO的适应度函数。FT指标的计算公式如下：

式中：C为检索模型所在类的模型总数；R表示前C－1个检索结果中相关模型的数量。根据式（5）可知，FT指标的计算需要用到检索模型的类别信息，而在实际检索过程中，用户提交的检索模型其类信息未知。为此，本文采用文献［13］提出的预测相似类的概念。用M表示三维模型库，M＝｛mi｜i＝1，2，…n｝，用Q表示检索模型。使用式（3）计算mi与Q的相似度，称Q的最相似模型所在的模型类为Q的预测相似类。

相似度计算过程优化以DC分布矩阵为输入，通过多次迭代输出使得FT指标最大的系数向量为X。优化过程朝着FT指标增长的方向进行，FT指标越高检索结果越好。

1.3 算法整体流程

首先使用式（1）进行一次相似度计算，确定模型的预测相似类；然后，使用二进制PSO优化相似度计算过程，输出使得FT取得最大值的系数向量X以及对应的检索结果。检索流程如下：

1）用户提交检索模型Q；

2）使用式（1）计算Q与模型库中所有模型的相似度，确定Q的预测相似类，生成检索结果；

3）对相似度计算过程进行二进制PSO优化，确定最优系数向量X以及优化后的检索结果Re⁃trivel_Result；

4）返回Retrivel_Result的前K个模型。

2 算法时间复杂度分析

本节从DC分布矩阵构造、模型检索和二进制PSO优化3个方面来分析整个算法的时间复杂度。

1）构造DC分布矩阵的时间复杂度

分布矩阵的构造由两步完成：首先构造随机点；然后计算随机点之间的距离和法向夹角余弦，并进行统计。假设随机点数量为n，那么构造DC分布矩阵的时间复杂度为O（n2）

2）模型相似度计算的时间复杂度

假设分布矩阵的规模为n×m，三维模型库中的模型数量为k。模型相似度的时间复杂度为O（n×m×k）。

3）二进制PSO优化的时间复杂度

假设粒子数量为p，迭代次数为t，那么二进制PSO优化环节的时间复杂度为O（n×m×k×p×t）。

3 算法验证

以VS2010为集成开发环境，结合MATLAB（R2011b）实现了本文提出的检索算法。使用普渡大学建立的工程模型标准库（engineering shape benchmark，ESB）［14］对算法进行了验证。实验采用PC机，CUP为E5400，主频2.7 GHz，2 G内存。形状描述阶段生成1 024个随机点，形状分布矩阵规模为50×50；二进制PSO优化过程参数设置如下：学习因子w为1，粒子数量为50，迭代20次。检索试验过程中检索模型已从模型库中剔除。

本节共进行了两类检索实验。第一类：使用式（1）计算模型对应的DC分布之间的距离，意在验证本文提出的多特征联合的检索能力（下文用DC表示）；第二类：在DC分布的基础上，加入二进制PSO优化，使用式（2）计算模型相似度，意在验证优化环节的效果（下文用DC+PSO表示）。两类检索实验的结果均与D2算法进行了对比，其中部分检索实验的结果如表2所示。表2显示了部分检索实验的前9个相似模型的分布情况。3个检索模型分别取自ESB库的薄壁类、棱柱类和回转类。

在薄壁类模型的检索实验中，D2检索到3个相关模型，排名为①、③和④；DC检索到5个相关模型，排名为①、②、③、④和⑤；而DC+PSO检索到的相关模型为①、②、③、④、⑤、⑥和⑨。无论是从相关模型的数量还是排名来比较，DC+PSO的检索结果在3种算法中最优，DC次之，D2最差。在棱柱类模型的检索实验中，D2检索到的相关模型排在第①、②、⑧和⑨，DC为①、②、③、④和⑥，DC+PSO为①、②、③、④、⑤、⑦和⑧，同样是DC+PSO最优，DC次之，D2排在第3位。在回转类模型试验中，D2检索到的相关模型为①、②、③、⑤、⑥、⑧和⑨，DC为相关模型，但DC+PSO相关模型排名更高。

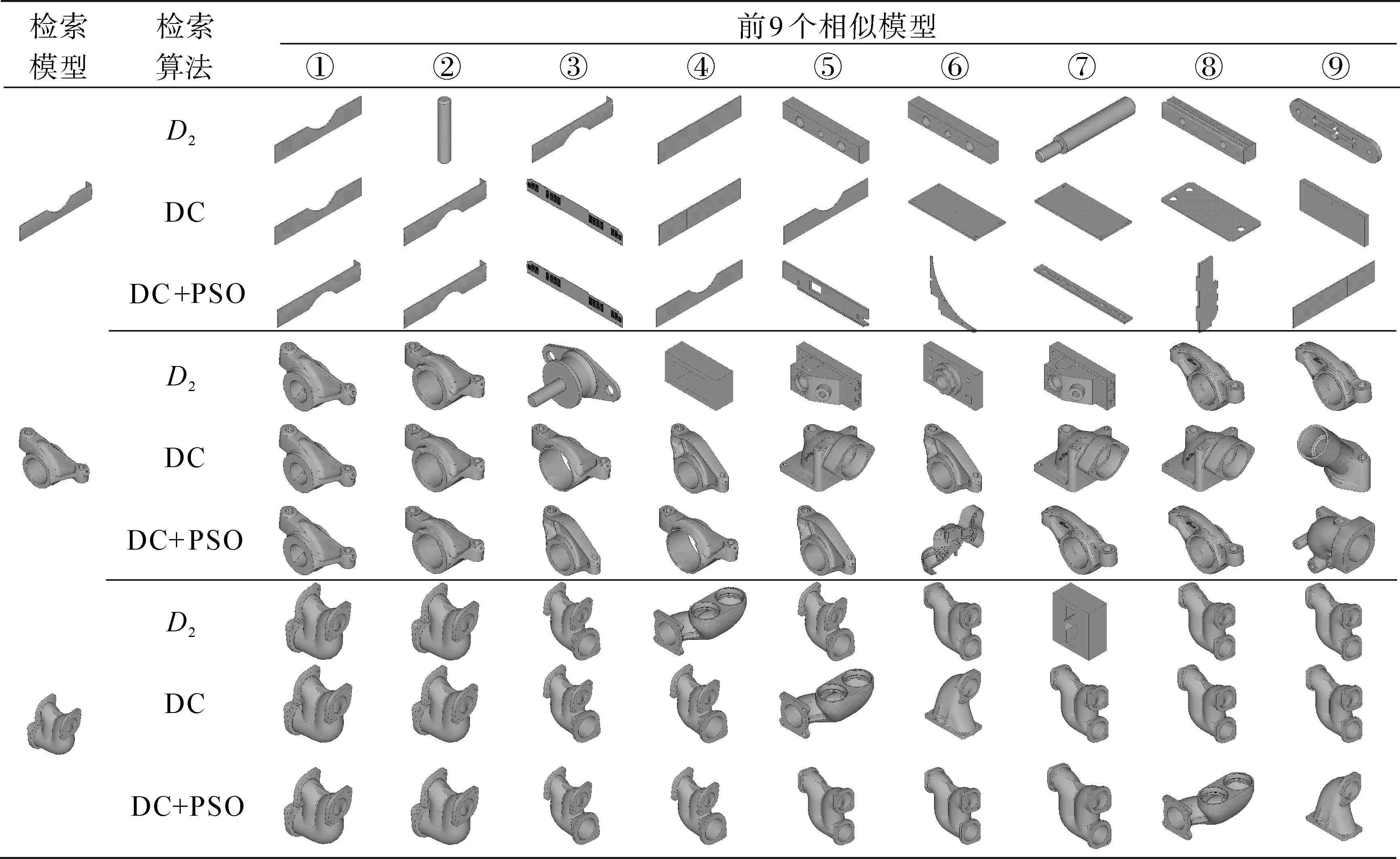
表2 距离－余弦联合形状分布示例Table 2 Examples of distance⁃cosine distribution

表3为D2、DC和DC+PSO关于薄壁类、棱柱类、回转类以及ESB全库的平均查准率对比。从表3的数据可以看到，DC+PSO检索性能明显优于D2和DC；DC在薄壁类和棱柱类上的检索性能优于D2，在回转类上略逊于D2。图2为DC、DC+PSO与几种典型检索算法（D2［5］、光场描述子［15］、特征临界点［16］以及测地连接图［17］等）在ESB全库上的平均查全率－查准率（Recall⁃Precision）曲线对比。从查全⁃查准曲线对比上来看，DC+PSO的检索性能略优于光场算法，明显优于其他几种算法。

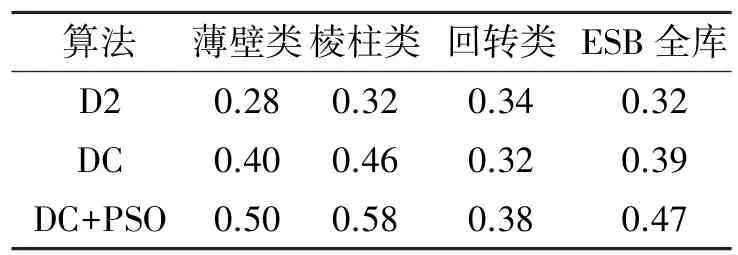
表3 D2、DC和DC+PSO 3种算法的平均查准率对比Table 3 Average precision of D2，DC and DC+PSO

本文采用FT（first⁃tier）、ST（second⁃tire）、NN（nearest neighbor）以及DCG（discounted cumulative gain）等4类指标［12］对3种算法（D2、DC和DC+ PSO）的检索性能进行了评价，并统计了其在分布矩阵构造与模型检索阶段的时间消耗，具体内容如表4所示。表4中的数据显示：DC算法的检索性能全面优于D2，FT、ST和NN指标增幅明显，说明多特征联合有效提高了算法的检索能力。与DC相比，DC+PSO的检索性能进一步提高，FT指标增长到50%，优化效果明显。但由于增加了优化环节，所以时间消耗有所增加。

图2 球面冲击波作用于刚性平板Fig.2 The spherical shock wave acting on a rigid plate

表4 算法性能的定量比较Table 4 Performance metrics comparison

4 结论

针对D2算法的不足，提出了基于随机点距离－法向夹角余弦分布和二进制PSO优化的三维工程网格模型检索算法。该算法通过统计随机点之间的距离与法向夹角余弦构造距离⁃余弦二维联合分布矩阵，以此矩阵对模型进行描述；在相似度计算环节，为了消除噪音数据对检索带来的影响，以检索结果最优为目标，采用二进制粒子群优化对分布矩阵的行向量进行筛选，将相似度计算限制在保留下来的行向量之间。实验结果表明本文算法可有效提高三维工程网格模型的检索效率。

在本文中，预测相似类是二进制粒子群优化适应度函数的计算依据。简言之，错误的预测相似类将导致优化过程失去意义，优化后检索结果的优劣性不可知。所以提高预测相似类的准确度是后续研究的重点。

［1］YER N，JAYANTI K，LOU K Y，et al.Three dimensional shape searching：state⁃of⁃the⁃art review and future trends［J］.Computer⁃Aided Design，2005，37（5）：509⁃530.

［2］TANGELDER J W H，VELTKAMP R C.A survey of con⁃tent based 3D shape retrieval methods［J］.Multimedia Tools and Applications，2008，39（3）：441⁃471.

［3］JAYANTI S，KALYANARAMAN Y，RAMANI K.Shape⁃based clustering for 3D CAD objects：a comparative study of effectiveness［J］.Computer⁃Aided Design，2009，41（12）：999⁃1007.

［4］杨育滨，林晖，朱庆.基于内容的三维模型检索综述［J］.计算机学报，2004，27（10）：1297⁃1310.

YANG Yubin，LIN Hui，ZHU Qing.Content⁃based 3D model retrieval：a survey［J］.Chinese Journal of Comput⁃ers，2004，27（10）：1297⁃1310.

［5］OSADA R，FUNKHOUSER T，CHAZELLE B，et al.Shape distributions［J］.ACM Transactions on Graphics，2002，21（4）：807⁃832.

［6］IP C Y，LAPADAT D，SIEGER L，et al.Using shape distri⁃butions to compare solid models［C］／／Proceedings of the 7th ACM Symposium on Solid Modeling and Applications.New York，USA：ACM，2002：17⁃23.

［7］王洪申，张树生，张开兴，等.基于法向分类的三维模型形状分布检索算法［J］.计算机集成制造系统，2009，15（6）：1187⁃1193.

WANG Hongshen，ZHANG shusheng，ZHANG Kaixing，et al.Shape distributions retrieval algorithm of 3D CAD models based on normal direction［J］.Computer Integrated Manufac⁃turing System，2009，15（6）：1187⁃1193.

［8］DARAS P，AXENOPOULOS A，LITOS G.Investigating the effects of multiple factors towards more accurate 3⁃D object retrieval［J］.IEEE Transaction on Multimedia，2012，14（2）：374⁃388.

［9］王洪申，张树生，白晓亮，等.三维CAD曲面模型距离⁃曲率形状分布检索算法［J］.计算机辅助设计与图形学学报，2010，22（5）：762⁃770.

WANG Hongshen，ZHANG Shusheng，BAI Xiaoliang，et al.3D CAD surface model retrieval algorithm based on distance and curvature distributions［J］.Journal of Computer⁃Aided Design＆Computer Graphics，2010，22（5）：762⁃770.

［10］KENNEDY J，EBERBART R C.Particle swarm optimiza⁃tion［C］／／Proceedings of IEEE International Conference on Neural Networks.（s.l.）：IEEE Press，1995：1942⁃1948.

［11］KENNEDY J，EBERBART R C.A discrete binary version of the particle swarm algorithm［C］／／Proceedings of the 1997 IEEE International conference on Systems，Man，and Cybernetics.（s.l.）：IEEE Press，1997：4104⁃4108.

［12］SHILANE P，MIN P，KAZHDAN M，et al.The Princeton shape benchmark［C］／／Proceedings of Shape Modeling International SMI 2004.Genove，Italy，2004：167⁃178.

［13］LI B，JOHAN H.3D model retrieval using hybrid features and class information［J］.Multimedia Tools and Applica⁃tions，2013，62（3）：821⁃846.

［14］JAYANTI S，KALYANARAMAN Y，IYER N，et al.De⁃veloping an engineering shape benchmark for CAD models［J］.Computer⁃Aided Design，2006，38（9）：939⁃953.

［15］CHEN D Y，OUHYOUNG M.On visual similarity based 3D model retrieval［J］.Computer Graphics Forum，2003，22（3）：223⁃232.

［16］侯鑫，张旭堂，金天国，等.基于网格临界点的三维工程模型检索算法［J］.计算机集成制造系统，2009，15（1）：72⁃81.

HOU Xin，ZHANG Xutang，JIN Tianguo，et al.3D engi⁃neering models retrieval algorithm based on mesh salient critical［J］.Computer Integrated Manufacturing System，2009，22（3）：223⁃232.

［17］张旭堂，陈晓峰，蒋立军，等.基于局部特征提取的棱柱类零件三维模型检索［J］.计算机集成制造系统，2012，18（3）：458⁃465.

ZHANG Xutang，CHEN Xiaofeng，JIANG Lijun，et al.Prismatic parts 3D model retrieval based on local shape factures extraction［J］.Computer Integrated Manufacturing System，2012，18（3）：458⁃465.

3D engineering model retrieval algorithm based on multiple features and similarity calculation optimization

ZHUANG Ting，ZHANG Xutang，HOU Zhenxiu
（School of Mechanical Engineering，Harbin Institute of Technology，Harbin 150001，China）

This paper proposes a retrieval algorithm based on the binary particle swarm optimization（PSO）and the joint distribution including the distance between every two random points and the normal included angle cosine in or⁃der to improve the retrieval accuracy of 3D engineering triangular mesh model.Firstly，numerous sample points on the surface of the model are randomly chosen.Next，the distances and the cosine values of the normal angles among the sample points are calculated.Finally，a two⁃dimensional grid with the distance and the cosine value as the coordinate axes is established.The joint distance⁃cosine shape distribution matrix of the 3D model is constructed through the sta⁃tistic data of sample points acquired in each mesh，using the distance L2between distribution matrixes to represent similarity between models.In order to demonstrate the different influence of shape distribution elements on the simi⁃larity in 3D models efficiently，binary PSO is employed to ameliorate the similarity computing process.Experimental results showed that the approach could improve the retrieval accuracy of engineering mesh models effectively.

3D model retrieval；content⁃based retrieval；multi⁃feature；distance⁃cosine distribution；similarity cal⁃culation；binary PSO

10.3969／j.issn.1006⁃7043.201312089

http：／／www.cnki.net／kcms／detail／23.1390.U.20150414.1613.010.html

TP391

A

1006⁃7043（2015）05⁃0720⁃05

2013⁃12⁃26.网络出版时间：2015⁃04⁃14.

国家自然科学基金资助项目（51001121）.

庄廷（1982⁃），男，博士研究生；

侯珍秀（1958⁃），女，教授，博士生导师.

庄廷，E⁃mail：zt_hit＠126.com.