T型三电平逆变器的共模电压及其抑制算法
2015-06-15王全东常天庆李方正苏奎峰
王全东, 常天庆, 李方正, 苏奎峰, 张 雷
(装甲兵工程学院控制工程系, 北京 100072)
T型三电平逆变器的共模电压及其抑制算法
王全东, 常天庆, 李方正, 苏奎峰, 张 雷
(装甲兵工程学院控制工程系, 北京 100072)
对T型逆变器共模电压的产生机理进行了分析,推导了PWM控制下逆变器共模电压的Fourier表达式,分析了其谐波成分及数学含义。阐述了传统SPWM、SVPWM算法的调制原理,对逆变器分别采用2种算法时的共模电压进行了仿真分析,并提出了减小共模电压的改进算法。为完全消除共模电压,采用了一种调制波移相PWM算法,并通过仿真验证了该算法的有效性。最后对各种算法下逆变器的共模电压、线电压等参数进行了对比分析。
T型逆变器;PWM;共模电压;抑制算法
与传统的两电平逆变器相比,多电平逆变器具有功率容量大、电压应力小和谐波含量低等诸多优势[1-2],在光伏并网、交流调速等高电压、大功率逆变领域的应用日益广泛。T型逆变器是一种改进型的中点箝位型(Neutral Point Clamp,NPC)三电平拓扑,它利用一个双向开关来实现中性点对地的箝位功能,与二极管箝位型(I型)三电平逆变器相比,其结构简单、可靠性高,而且开关上下桥臂的损耗较为均衡[3-4],应用前景较为广阔,是近年来多电平逆变器领域的研究热点。
逆变器控制中普遍采用脉宽调制(Pulse Width Modulation,PWM)技术,其在逆变器负载中性点处会产生共模电压。共模电压会加速电机轴承老化、降低电机寿命[5],作用于逆变器的对地寄生电容时会产生共模电流,不但增加了负载损耗,而且会对逆变器的控制系统以及周围的敏感电子设备构成严重干扰[6-7],给逆变器自身以及电机等负载设备带来了一系列的负面效应。
目前,对共模电压的抑制主要有硬件和软件2种方法:硬件方法是通过在逆变器中外加无源或有源滤波器的方式减小共模电压,但共模滤波器的设计较为复杂,会造成逆变器体积和成本的显著增加[8],滤波的效果也不理想;软件方法通过改进现有PWM调制算法从源头对共模电压进行抑制,既可以省去滤波器的成本,又不会增加原有拓扑的复杂性,已成为解决共模电压问题的重要方法。因此,本文采用软件的方法对T型逆变器共模电压进行抑制,并通过仿真对算法进行验证。
1 共模电压
带电机负载的三相T型三电平逆变器拓扑如图1所示(不含滤波电路)。其中:Cdc1、Cdc2为直流分压电容;O为直流电压中点;La′、Lb′、Lc′为电缆电感;Ra′、Rb′、Rc′为电缆电阻;La、Lb、Lc为电机负载三相绕组的等效电感;Ra、Rb、Rc为电阻负载三相绕组的等效电阻。
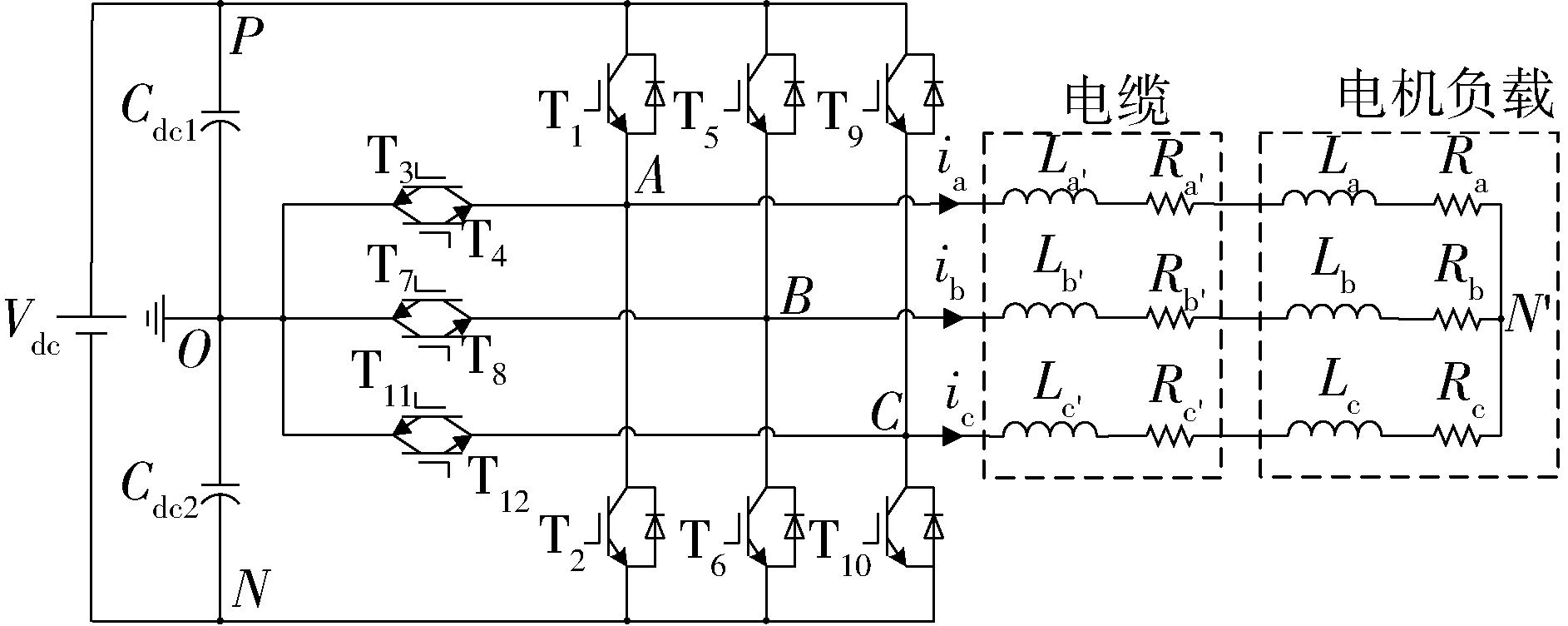
图1 带电机负载的三相T型三电平逆变器拓扑
以O点为参考点,三相桥臂中点A、B、C对中性点N′的电压分别为
(1)
根据图1,由基尔霍夫电压定律可得
(2)
假设电缆及电机的三相参数对称,即
(3)
将式(3)代入式(2),并对uAN′、uBN′、uCN′求和可得
uAN′+uBN′+uCN′= 3(L′+L)d(ia+ib+ic)/dt+
3(R′+R)(ia+ib+ic)。
(4)
对于三相对称感应电机,存在
ia+ib+ic≈0,
(5)
将式(5)代入式(4)可得
uAN′+uBN′+uCN′=0,
(6)
将式(6)代入式(1)可得
uON′=-(uAO+uBO+uCO)/3。
(7)
在三相PWM逆变器中,共模电压定义为逆变器输出中点N′对参考地的电位差[9]。则三相T型逆变器的共模电压为
uCM=uN′O=-uON′=(uAO+uBO+uCO)/3。
(8)
图2为A相输出电压uAO的仿真波形,在1个工作周期内,其关于点(Ts/2,0)成镜像对称。
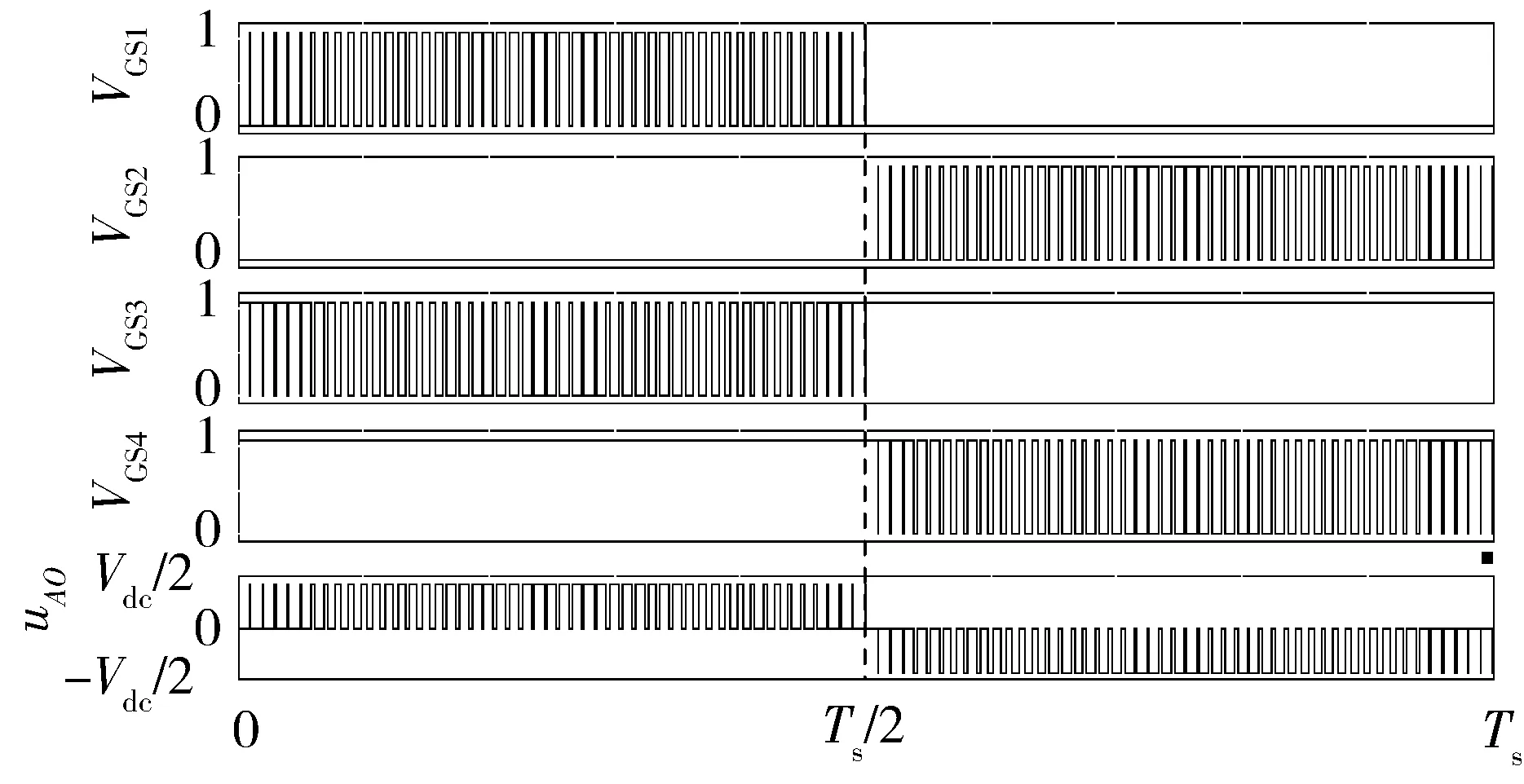
图2 A相输出电压uAO仿真波形
令调制比M=VS/VC,载波比N=ωC/ωS,其中:VS、VC分别为调制波、载波峰值电压;ωS、ωC分别为调制波、载波的频率。则根据贝塞尔函数可得uAO的Fourier级数表达式为
uAO= (Vdc/2)Msin(ωSt-φ)+(Vdc/π)×
sin{[mN±(2n-1)]ωSt},
(9)式中:Jn为贝塞尔函数[10];φ为三角载波与调制波不同步时二者的相位差。而当载波比N为3的整数倍时,B、C相的波形也为镜对称,此时的共模电压为
uCM=(uAO+uBO+uCO)/3=Vdc/2+(Vdc/π)×
cos{[mN±3(2n-1)]ωSt)。
(10)
由式(10)可知:共模电压所包含的电压频谱中不存在开关频率次谐波及其m次开关谐波(m=1,2,…),而只存在其边频带。当载波与三相调制波均同步时,边频带的幅值和相位分别为
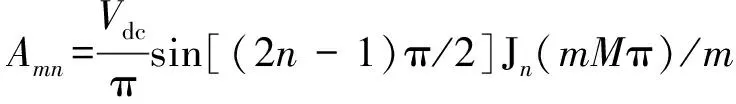
(11)
φmn=(2n-1)φA。
(12)
式中:φA为A相调制波相位。
开关频率f=15 kHz=300fs(fs=50 Hz,为工频频率)时,共模电压uCM的FFT分析结果如图3所示。可见:FFT分析结果与上述理论分析结果一致,频谱中mN±3次谐波的幅值较大。
图3 f=15 kHz时共模电压FFT分析结果
2 SPWM及其改进算法
2.1 SPWM算法
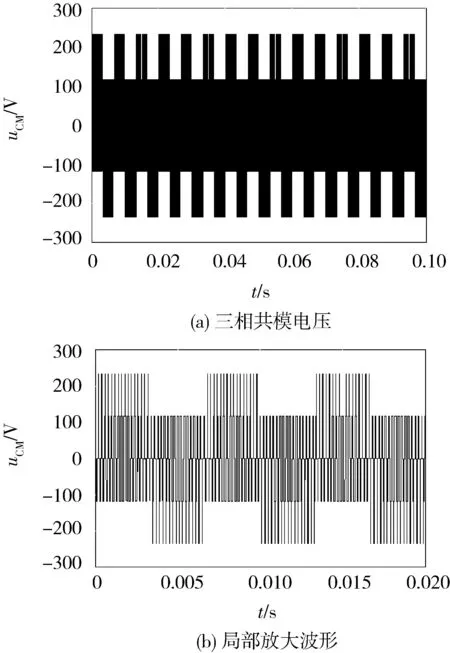
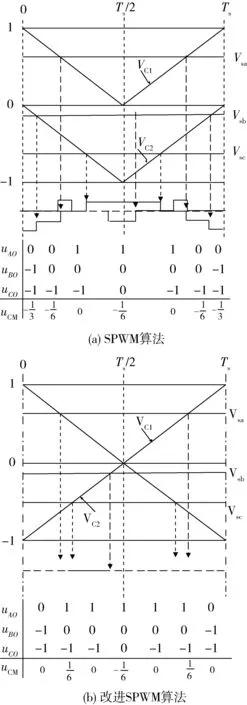
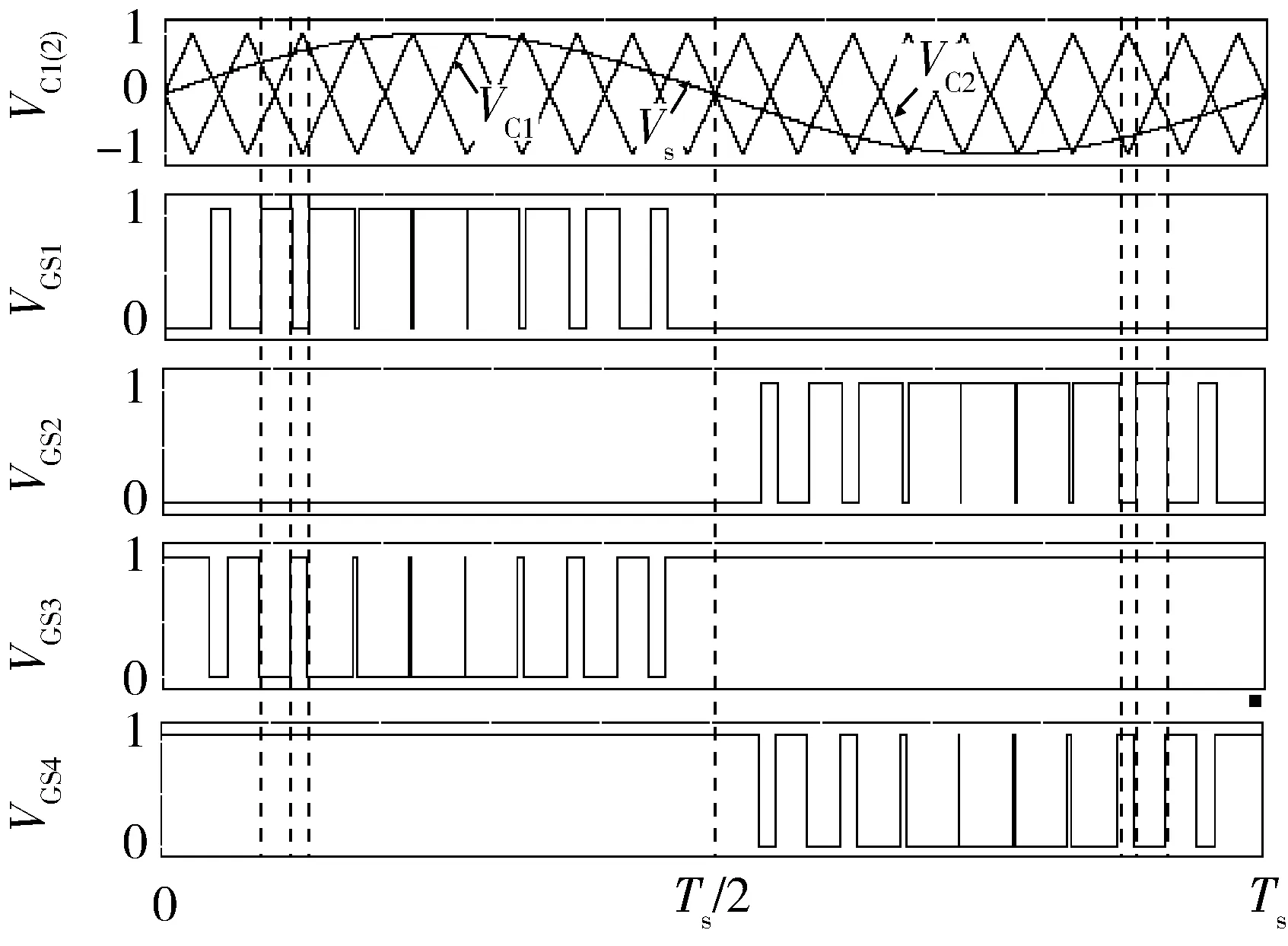
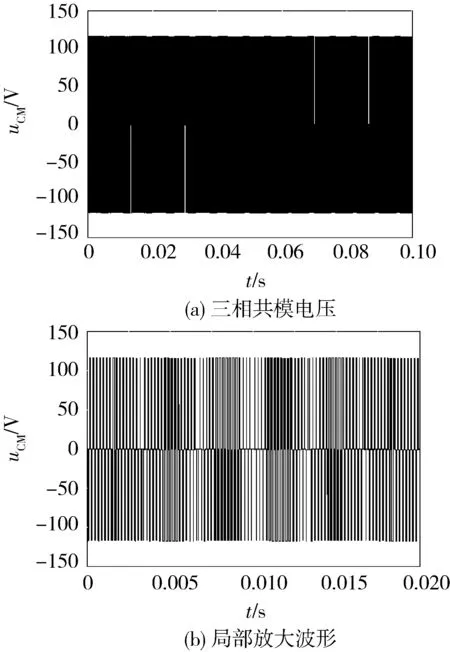
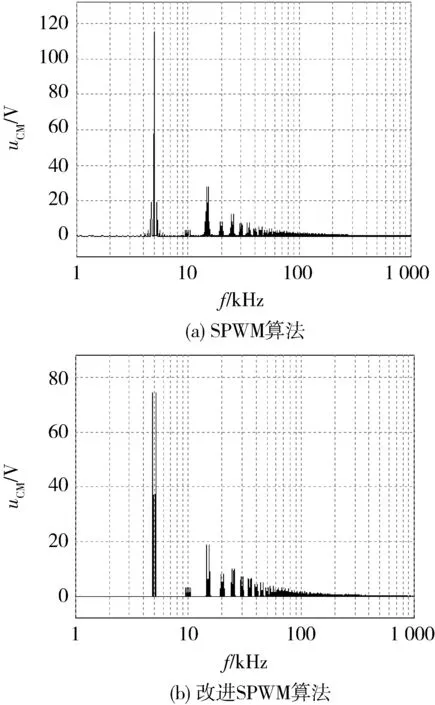
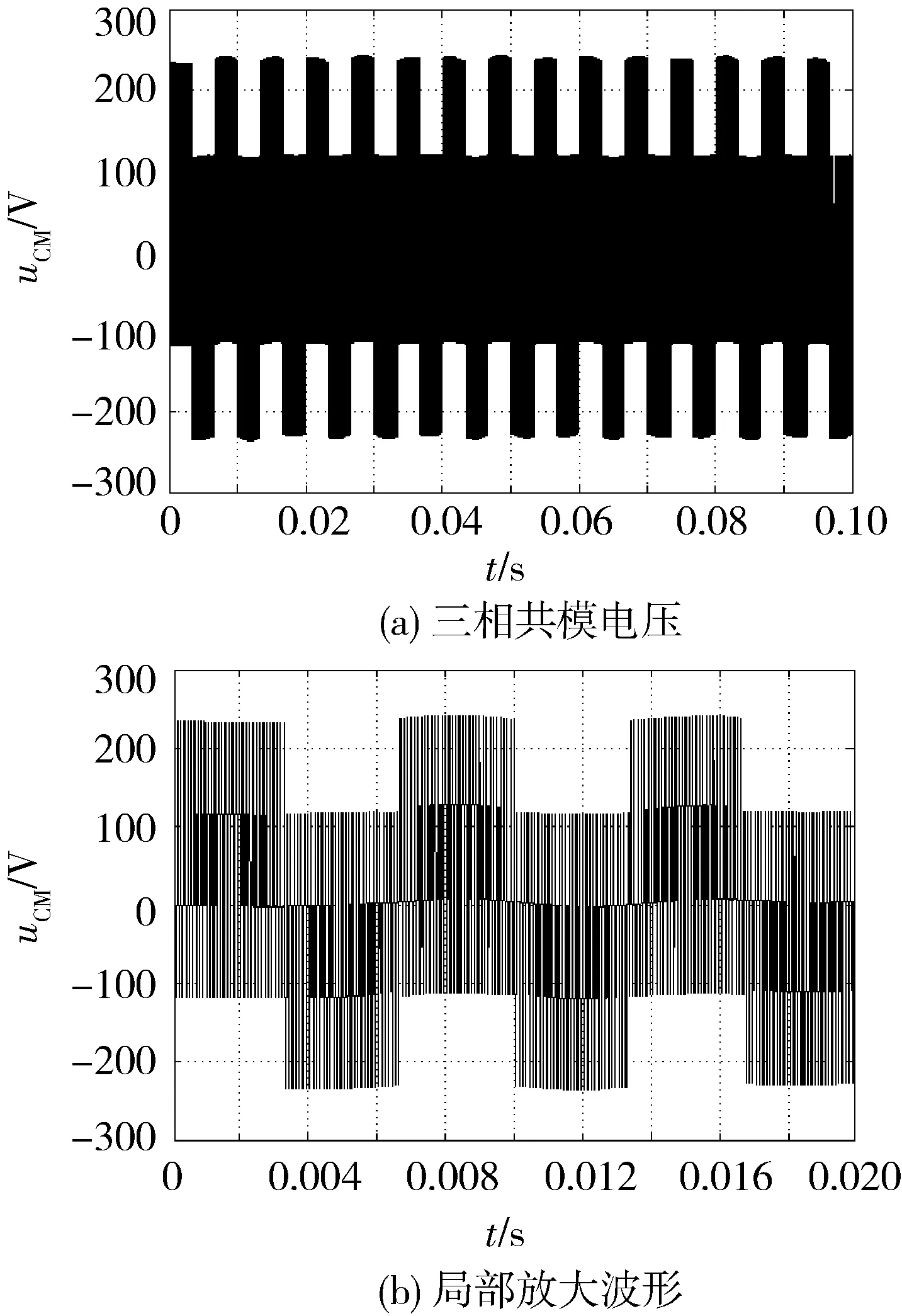
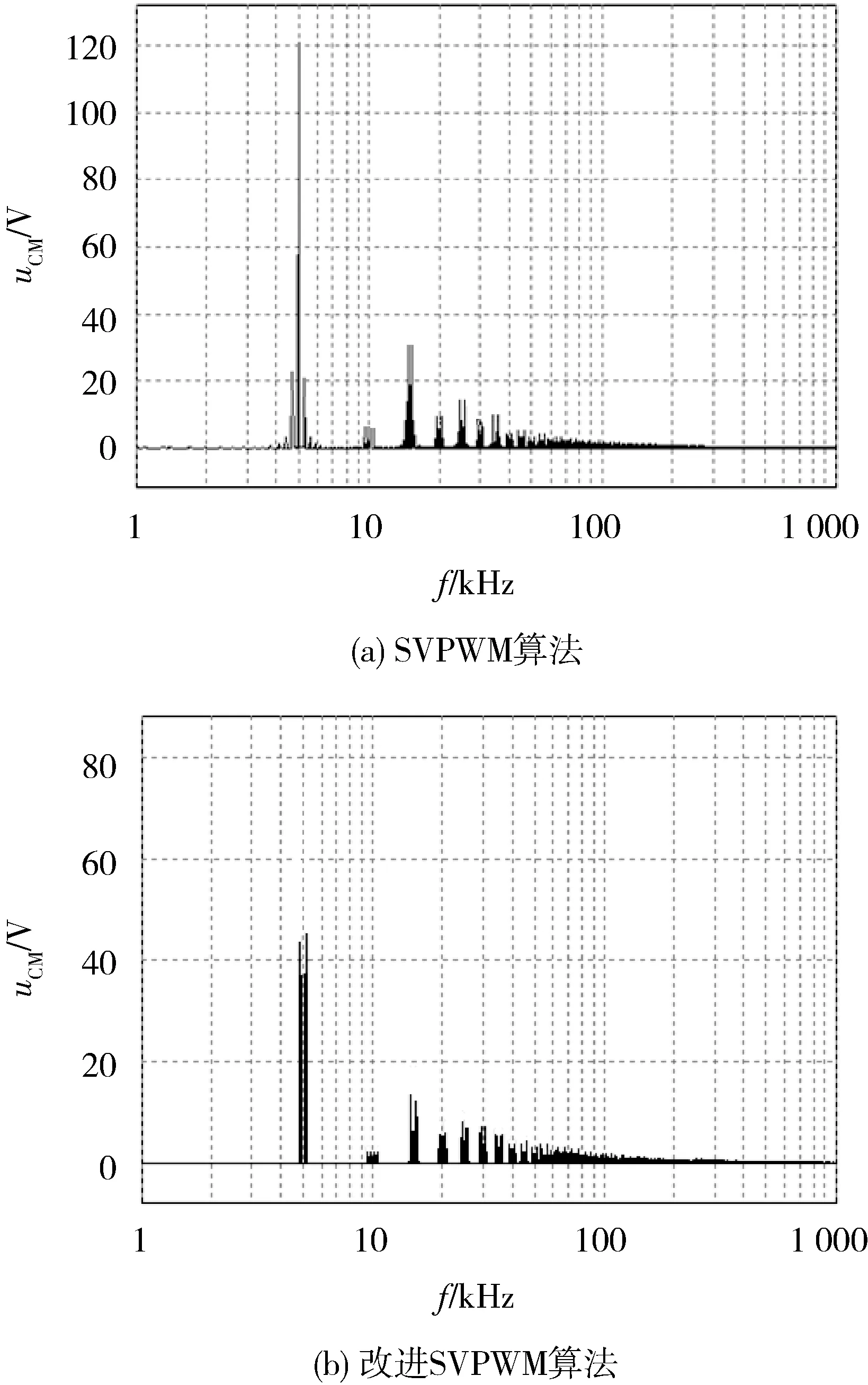
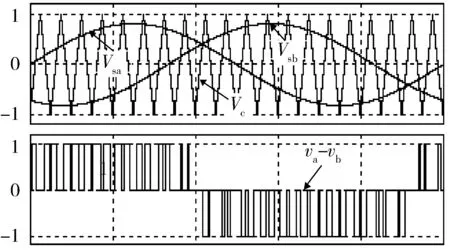
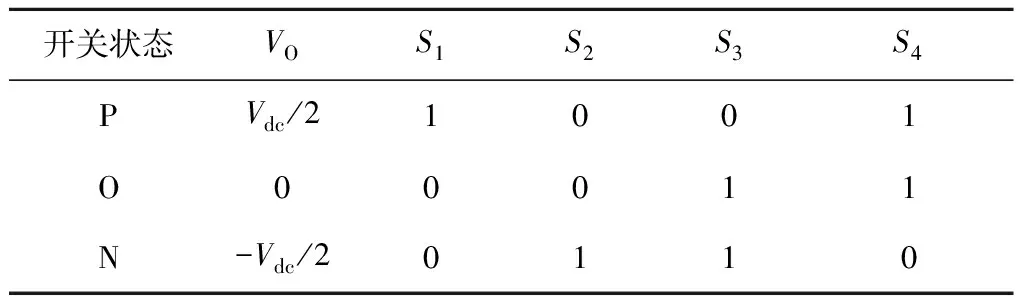
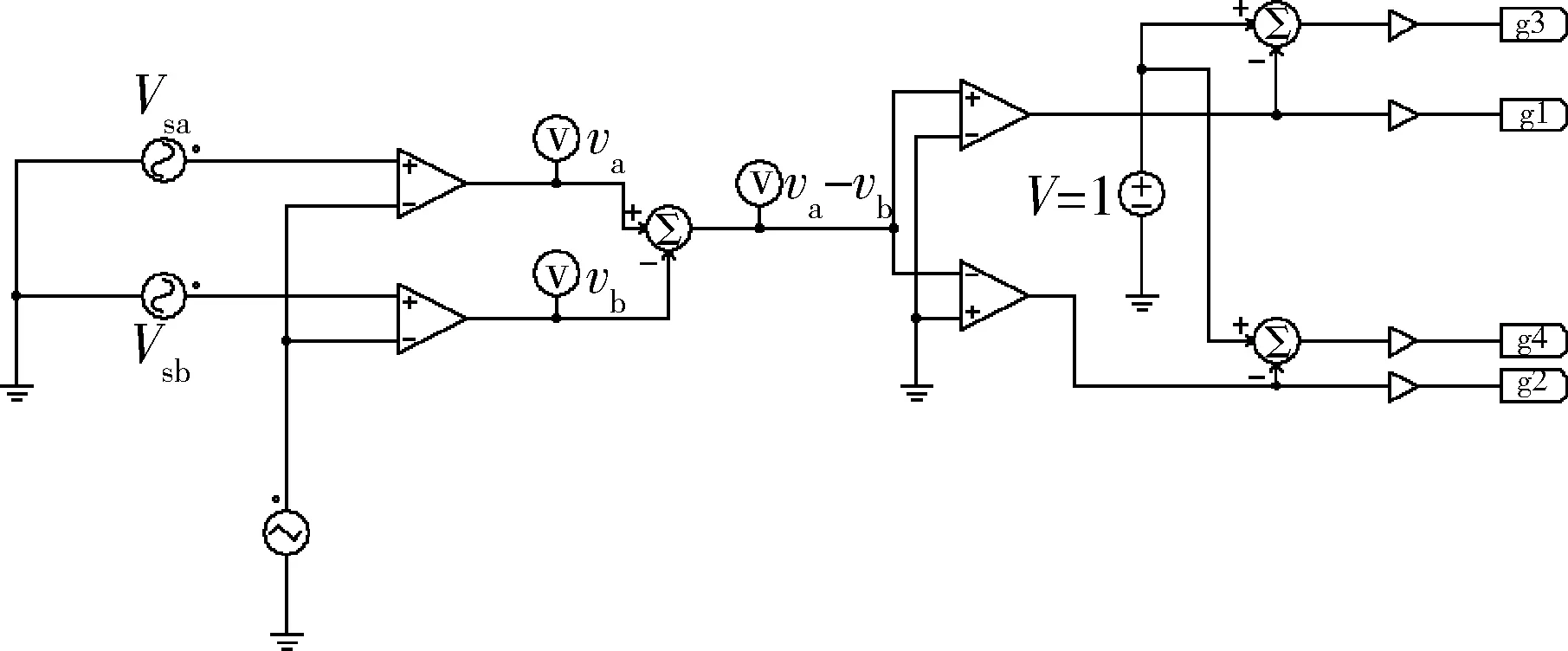
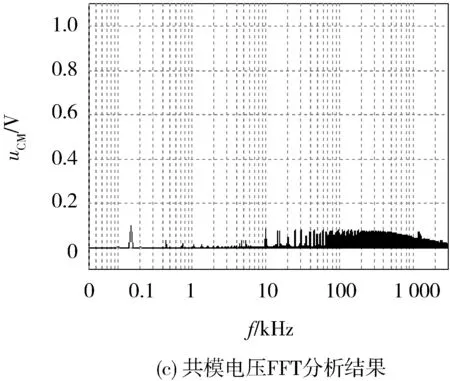
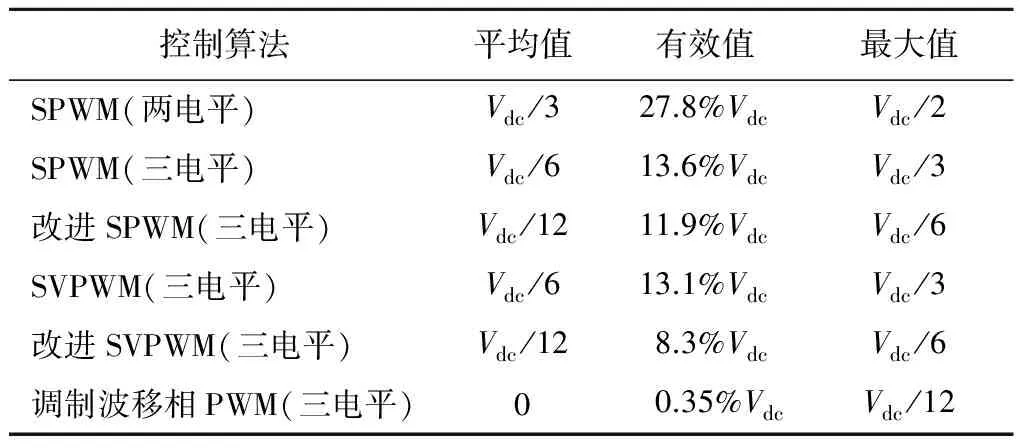
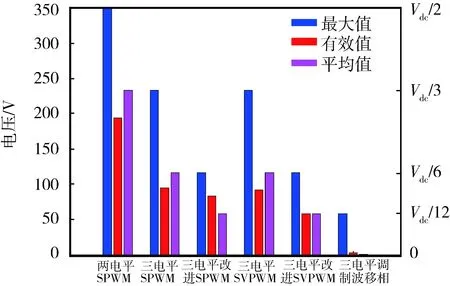
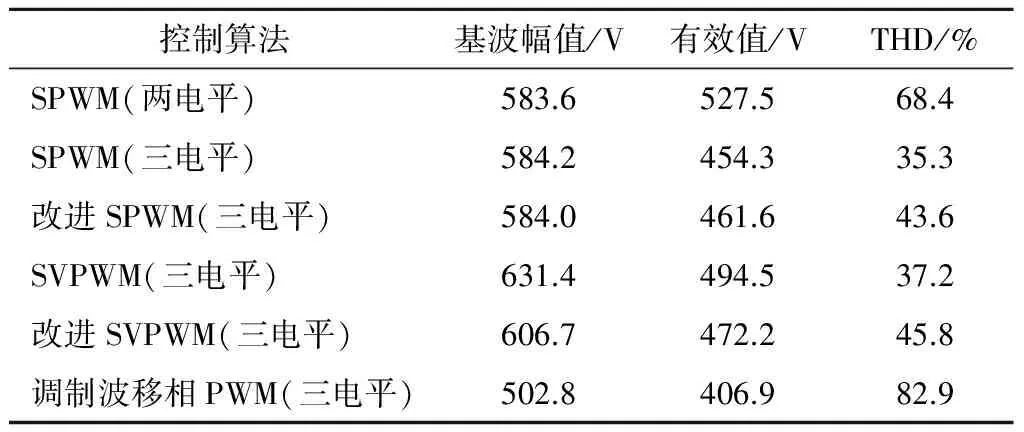
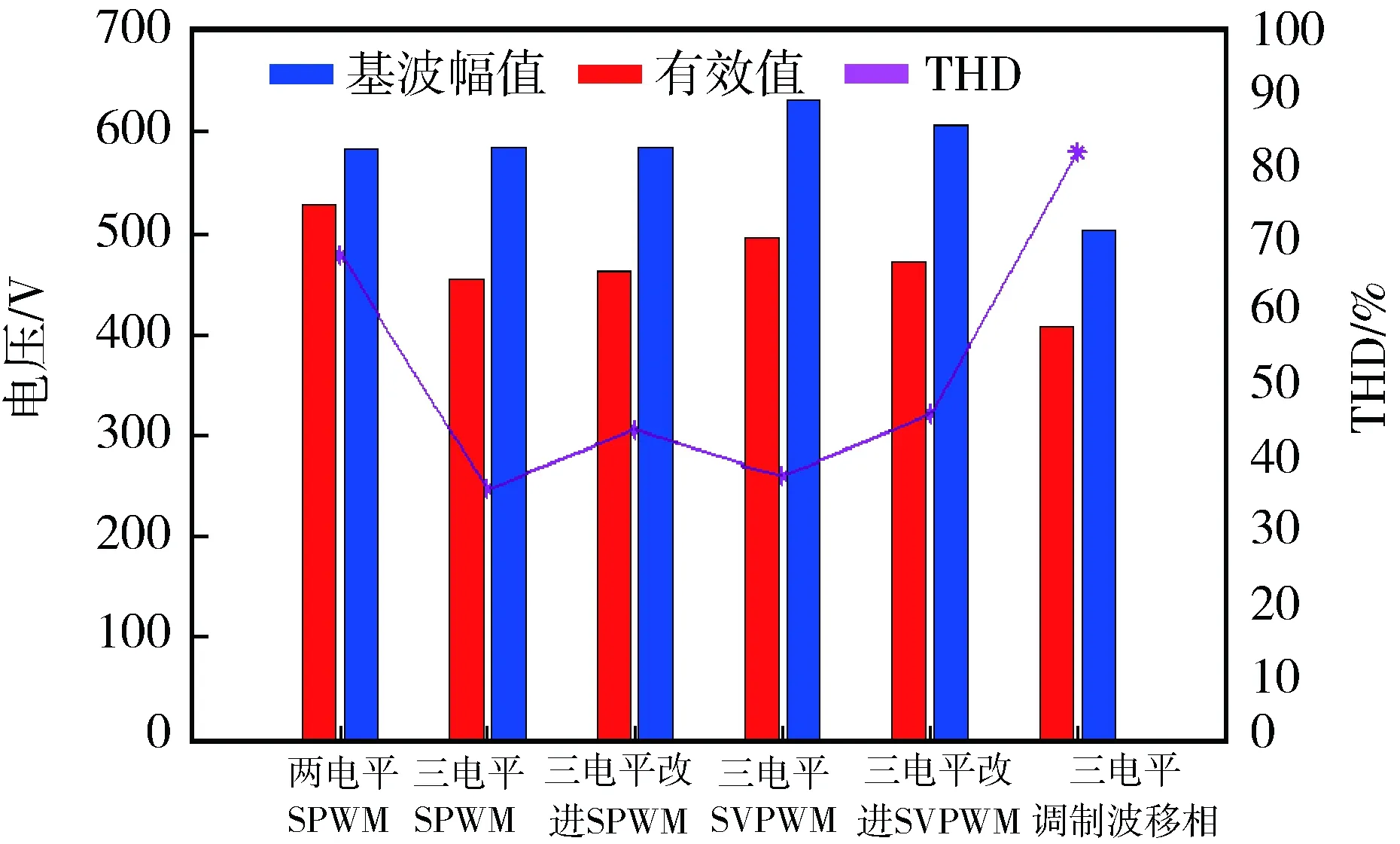
正弦波脉冲宽度调制(Sine Pulse Width Modulation,SPWM)算法被广泛用于两电平及多电平逆变器的控制之中。对于N电平逆变器,每相需要1路正弦调制波信号和N-1路三角载波信号,具体到本文的三电平逆变器,其SPWM控制策略的控制逻辑如图4所示。其中:VC1、VC2为2路同相位三角载波(VC1位于x轴上方,VC2位于x轴下方);Vs为正弦调制波。在(0,Ts/2)区间内,驱动信号VGS2恒为0,VGS4恒为1,当Vs>0且Vs>VC1时,VGS1=1,VGS3=0,当Vs>0且Vs 图4 SPWM算法控制逻辑 在SPWM算法控制下,三相T型逆变器的共模电压及其局部放大波形如图5所示。 图5 SPWM算法三相共模电压及其局部放大波形 2.2 SPWM改进算法 采用SPWM控制算法时的共模电压如图6(a)所示,uCM绝对值的最大值为Vdc/3。为了减小共模电压,将x轴下方的载波信号VC2右移半个载波周期,得到一种改进SPWM调制算法,如图6(b)所示,可将uCM绝对值的最大值减小为Vdc/6。 改进SPWM算法的控制逻辑如图7所示,其中:VC1、VC2为关于x轴对称的2路相位相差180°的三角载波;Vs为正弦调制波。在(0,Ts/2)区间内,驱动信号VGS2恒为0,VGS4恒为1,当Vs>0且Vs>VC1时,VGS1=1,VGS3=0,当Vs>0且Vs 在改进SPWM算法控制下,三相T型逆变器的共模电压及其局部放大波形如图8所示。可以看出:采用改进SPWM算法时,共模电压的最大值由Vdc/3减小为Vdc/6。 图6 2种算法下的共模电压 图7 改进SPWM算法控制逻辑 图8 改进SPWM算法三相共模电压及其局部放大波形 2.3 对比分析 为了进一步分析改进SPWM算法对共模电压的抑制效果,共模电压在2种SPWM算法控制下的FFT分析结果如图9所示。可以看出:2种共模电压包含的谐波种类(频率)未变,但改进算法包含的谐波幅值较小,有效减小了逆变器的共模电压。 图9 共模电压在2种SPWM算法控制下的FFT分析结果 3.1 SVPWM算法 SVPWM控制策略的核心思想是使每个开关周期内逆变器输出电压的Park变换与期望输出的三相正弦波电压合成的空间矢量等效[11],该算法比较成熟,而且在PWM逆变器的控制中应用广泛。 在SVPWM算法控制下,三相T型逆变器的共模电压及其局部放大波形如图10所示,由于SVP-WM算法是采用空间矢量实现SPWM算法的一种形式,其本质与传统SPWM算法无异,因此其线电压及共模电压的仿真波形与传统SPWM算法一致。 图10 SVPWM算法三相共模电压及其局部放大波形 3.2 SVPWM改进算法 单相T型逆变器输出电压有正、零、负三种极性,分别对应逆变器的P、O、N三种开关状态。则三相T型逆变器一共存在33=27种开关状态,表1为各开关状态下的共模电压。 传统的SVPWM 调制包含了上述27种开关状态,uCM的值在-Vdc/2~Vdc/2 之间变化,共模电压较大。如果仅选用uCM为0的7种开关状态,虽然uCM降到0,但是较少的电压矢量会造成参考电压过渡不平滑,逆变器输出波形变差,谐波含量THD(Total Harmoic Distortion)较高。将两者折中考虑,对传统的SVPWM算法进行改进,选用uCM为Vdc/6、0、-Vdc/6的3类开关状态(19种),这样uCM的值降到-Vdc/6~Vdc/6之间,且输出波形质量得到保证。在19矢量的SVPWM调制中,每个电压矢量对应的开关状态无冗余。 表1 各开关状态下的共模电压 改进SVPWM算法的原理与其传统算法一致,主要差别在于矢量顺序及时间分配,其也必须满足减少开关动作次数和矢量对称的要求,改进前后的SVPWM算法在扇区1区间1内的矢量顺序及时间分配如图11所示,其余区间同理可得。 图11 改进前后的SVPWM算法在扇区1区间1内的矢量顺序及时间分配 在改进SVPWM算法控制下,三相T型逆变器的共模电压及其局部放大波形如图12所示。可见:采用改进SVPWM算法时,共模电压的最大值由Vdc/2减小为Vdc/6。 图12 改进SVPWM算法三相共模电压及其局部放大波形 3.3 对比分析 为了进一步分析改进SVPWM算法对共模电压的抑制效果,在2种SVPWM算法控制下的共模电压FFT分析结果如图13所示。可见:2种共模电压包含的谐波种类(频率)未变,但改进算法包含的谐波幅值明显减小,有效减小了逆变器的共模电压。 图13 在2种SVPWM算法控制下的共模电压FFT分析结果 4.1 算法实现 改进型的SPWM、SVPWM与其传统算法相比,都可以有效减小逆变器的共模电压,但无法将其完全消除,主要原因仍在于PWM调制无法保证所有时刻三相输出电压之和为0。在此,采用一种调制波移相的PWM调制方式,如图14所示。首先,将正弦调制波Vsa移相120°得到调制波Vsb;然后分别与三角载波进行比较,得到2组调制信号va和vb;最后结合表2中输出电压与开关状态,通过PWM控制将va-vb转化为三电平逆变器的相电压波形,va-vb转化为A相四路控制信号逻辑电路,如图15所示。 图14 调制波移相PWM控制 表2 输出电压与开关状态 开关状态VOS1S2S3S4PVdc/21001O00011N-Vdc/20110 图15 va-vb转换为A相四路驱动信号 假设va、vb的幅值为1,则A相电压为 VAO=(Vdc/2)(va-vb), (13) 同理可得B、C相电压,则三相共模电压为 VCM= (VAO+VBO+VCO)/3=(Vdc/6)× [(va-vb)+(vb-vc)+(vc-va)]=0。 (14) 由此可知:采用调制波移相PWM控制方式,可以从理论上完全消除三相T型逆变器的共模电压。 4. 2 仿真分析 在调制波移相PWM算法控制下,三相T型逆变器的共模电压及其FFT分析结果如图16所示。可见:采用调制波移相PWM算法时,共模电压的最大值为Vdc/12,而且共模电压的谐波含量不同于传统的SPWM、SVPWM及其改进算法,此时的共模电压为开关动作产生的电压尖峰,不含输入电压且其持续时间为瞬间,因此其在频域内表现为大量幅值很小的高次谐波,几乎不含开关频率的低次谐波,极大地减小了逆变器的共模电压。 图16 调制波移相PWM算法仿真波形 4.3 算法比较分析 不同控制算法下共模电压的平均值、有效值及最大值如表3所示(两电平也考虑在内)。 表3 不同算法下共模电压平均值、有效值及最大值 对比分析表3可知: 1) 无论采用何种PWM调制方式,三电平逆变器的共模电压比两电平逆变器普遍要小; 2) 2种改进算法较其传统算法,可以在一定程度上抑制逆变器的共模电压; 3) 与其他算法相比,调制波移相PWM算法的共模电压抑制效果最显著。 不同控制算法下共模电压的平均值、有效值及最大值直方图如图17所示。 图17 不同控制算法下的共模电压平均值、有效值及最大值直方图 仿真中观察发现:采用不同PWM调制算法时,线电压的仿真结果存在差异,为了分析各算法对逆变器输出线电压的影响,将各算法下线电压(滤波前)的基波幅值、有效值和THD汇总如表4所示。 表4 不同算法下的线电压(滤波前)基波幅值、有效值和THD 不同控制算法下逆变器输出线电压的基波幅值、有效值和THD直方图如图18所示。 图18 不同控制算法下的线电压基波幅值、有效值和THD直方图 通过分析表4和图18可知: 1) 在相同条件下,两电平和三电平逆变器线电压的基波幅值基本相同,两电平逆变器线电压的有效值较大,直流电压利用率较高,但三电平逆变器线电压的THD(调制波移相PWM算法除外)要明显小于两电平,输出波形更接近正弦波且所需滤波器较小; 2) 改进SPWM算法与其传统算法的基波幅值和有效值基本一致,但它在减小共模电压的同时增加了线电压的THD; 3) 改进SVPWM算法的基波幅值和有效值较其传统算法有所下降,而且其为减小共模电压牺牲了部分矢量状态,使线电压的THD有所增加; 4) 调制波移相PWM算法虽在理论上可消除逆 变器的共模电压,但以牺牲线电压的正弦度为代价,导致输出线电压的基波幅值和有效值较小,存在直流电压利用率低和输出THD较大的缺点。 对现有PWM调制算法进行改进是解决逆变器共模电压问题的重要手段。本文通过对T型逆变器分别采用SPWM、SVPWM及其改进算法和调制波移相PWM算法进行仿真发现:改进SPWM、SVPWM算法可以在一定程度上抑制逆变器的共模电压;虽然调制波移相PWM算法抑制共模电压的效果显著,但其线电压THD较大,为了保证波形质量,需要很大的输出滤波器,这给逆变器的成本和功率密度带来不利影响。从电压利用率、共模电压和线电压THD等方面进行综合考虑,改进型SVPWM算法最具工程应用价值。 [1] 王付胜, 何立灿, 成晓潇, 等. 基于三电平中矢量的零共模电压算法研究[J]. 电力电子技术, 2012, 46(10):77-79. [2] 戴文君, 张兴, 王付胜, 等. 一种新颖的三电平光伏逆变器调制策略研究[J]. 电力电子技术, 2014, 48(1):4-6. [3] 王全东, 李方正. 基于RB-IGBT的T型逆变器中点电压控制技术仿真研究[J]. 通信电源技术, 2014, 31(3):39-41. [4] 王全东, 李方正, 孟宪波. 杂散参数对T型逆变器IGBT关断电压的影响与叠层母线设计[J]. 装甲兵工程学院学报, 2014, 28(6):64-70. [5] 毛承雄, 李维波, 陆继明, 等. 高压变频器共模电压仿真研究[J]. 中国电机工程学报, 2003, 23(9):57-62. [6] 钟玉林, 赵争鸣. 改进式SHEPWM对三电平变频器系统的共模电压和轴电压的抑制作用[J].电工技术学报,2009, 24(6):48-55. [7] 姜艳姝, 徐殿国, 赵洪, 等. 多电平SPWM变频器中共模电压抑制技术的研究[J]. 中国电机工程学报, 2005, 25(3):19-22. [8] 罗北, 和军平, 彭志辉, 等. 三电平光伏并网逆变器共模电压SVPWM抑制策略研究[J]. 电源世界, 2010, 16(6):21-25. [9] 裴雪军, 康勇, 熊健, 等. PWM逆变器共模传导电磁干扰的预测[J]. 中国电机工程学报, 2004, 24(8):83-88. [10] 姚端正,梁家宝. 数学物理方法[M]. 武汉:武汉大学出版社,2001:358-373. [11] 胡慧慧. 基于空间矢量控制的三电平逆变器的研究[D]. 青岛:中国石油大学(华东), 2008. (责任编辑:尚彩娟) Common-mode Voltage of T-shaped Three-level Inverter and Its Suppression Algorithm WANG Quan-dong, CHANG Tian-qing, LI Fang-zheng, SU Kui-feng, ZHANG Lei (Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China) The generating mechanism of T-shaped inverter common-mode voltage is analyzed, the Fourier expression of common-mode voltage under the control of PWM is deduced, and its harmonic components and mathematical meaning are analyzed. In addition, the modulation principles of traditional SPWM and SVPWM algorithms are expounded, the common-mode voltage of the inverter using the two algorithms is simulated and analyzed, and the ameliorated algorithm which can reduce common mode voltage is put forward. In order to eliminate completely the common-mode voltage,a modulation wave phase-shifted PWM algorithm is proposed, and its effectiveness is verified by simulation. Finally, common-mode voltage, line voltage and other parameters under various algorithms are compared and analyzed. T-shaped inverter; PWM; common-mode voltage; suppression algorithm 1672-1497(2015)04-0068-08 2015-03-30 王全东(1989-),男,博士研究生。 TM464 A 10.3969/j.issn.1672-1497.2015.04.014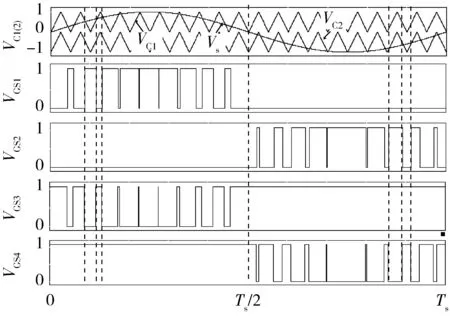
3 SVPWM及其改进算法


4 调制波移相PWM算法

5 结论
