基于冲量法实现航天器编队重构控制仿真的研究

刘 猛，池 云，张德育

（1.沈阳理工大学信息科学与工程学院，沈阳 110159；2.辽宁行政学院，沈阳 110161）

基于冲量法实现航天器编队重构控制仿真的研究

刘 猛1，池 云2，张德育1

（1.沈阳理工大学信息科学与工程学院，沈阳 110159；2.辽宁行政学院，沈阳 110161）

针对航天器编队重构的可视性不强，提出一种冲量法实现航天器编队重构的视景仿真技术。双脉冲机动是指航天器对空间目标的近轨道转移时，所需要的两次冲量机动。应用航天器之间相对运动原理，以空间目标轨道六要素为目标函数，通过调整航天器轨道参数对空间目标进行编队重构，有摆动绕飞转移至摆动式悬挂绕飞，进而得出了航天器转移摆动式悬挂绕飞编队到所需冲量基本关系，从而实现航天器对空间目标进行编队重构控制。

双脉冲机动，相对运动，编队重构，摆动式悬挂

0 引言

随着航天技术的迅猛发展，空间航天器的数量、水平及能力不断提高，各航天大国为了保持空间的优势，纷纷开展有关航天器机动性的研究。在此项研究中，航天器编队重构技术已成为其关注的焦点。为了提供航天器编队重构的直观显示，真实呈现航天器编队重构的任务过程，本文运用STK卫星工具仿真软件设计航天器编队重构控制仿真系统。

1 相对运动的双脉冲机动

航天器C相对于参考目标A的位置矢量δr0和速度δv0为已知，在t=0时刻进行脉冲机动，在时刻t=0+瞬间将速度变为δv0+。δv0+的分量如下页图1所示，要确定引入距阵标记来定义相对位置的矢量和速度矢量

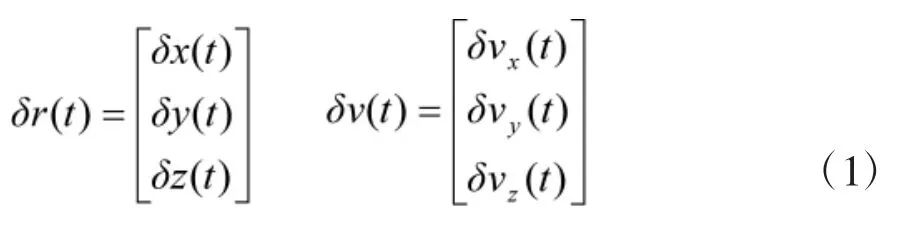
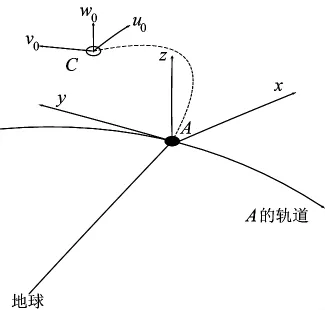
图1 轨道追踪相对轨道示意图

初始值为：

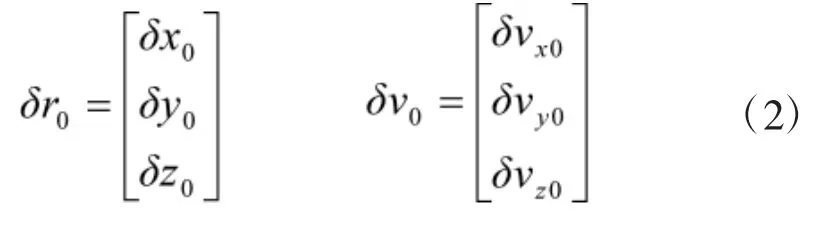
在交会分析中所有的运动量均是相对与C-W坐标而言利用矩阵可以进一步解为：

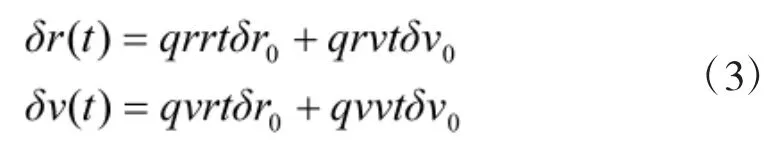
其中的C-W距阵为：

式（4）处的δu0+、δv0+、δw0+，以使C能于规定的tf时刻准确到达目标航天器处。将C置于交会轨道所需要的速度增量为：

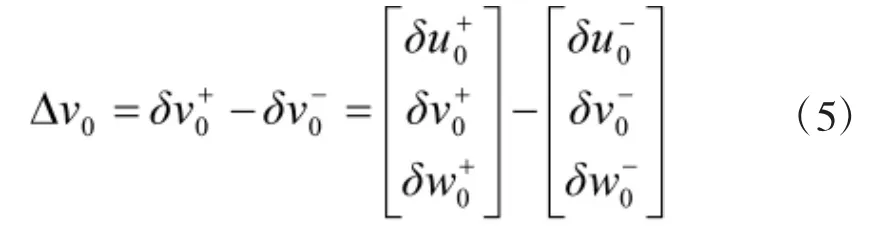
在tf时刻，C将到达运动坐标系的原点A处，即δrf=δr（tf）。在tf时刻的值，可得

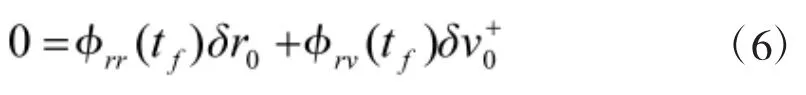
由此解出

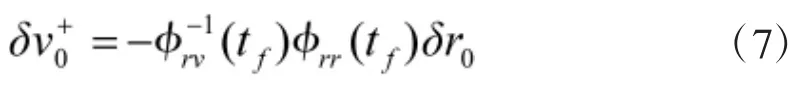
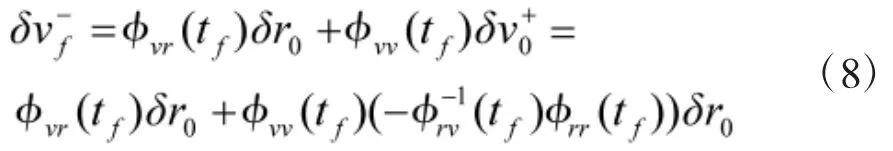
化简后，可得

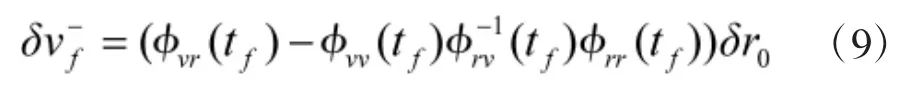
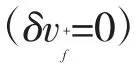
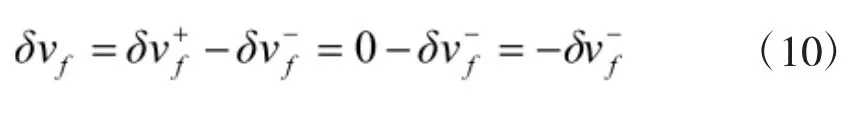
2 基于摆动式悬挂绕飞的轨道设计

摆动编队轨道构形中，参考目标和航天器均在圆轨道上运行，航天器在同一平面内相对参考目标作简谐运动，从参考飞行器的视角来看，航天器在参考的Z轴方向像“钟摆”一样的简谐运动，所以称其为钟摆式编队。假设参考参考目标A的轨道要素为（a，i，w，Ω，θ），空间虚拟航天器B的轨道六要素为（a1，i1，w1，Ω1，θ1），在赤道惯性坐标系中，参考目标与空间虚拟航天器的相对位置△r1为：

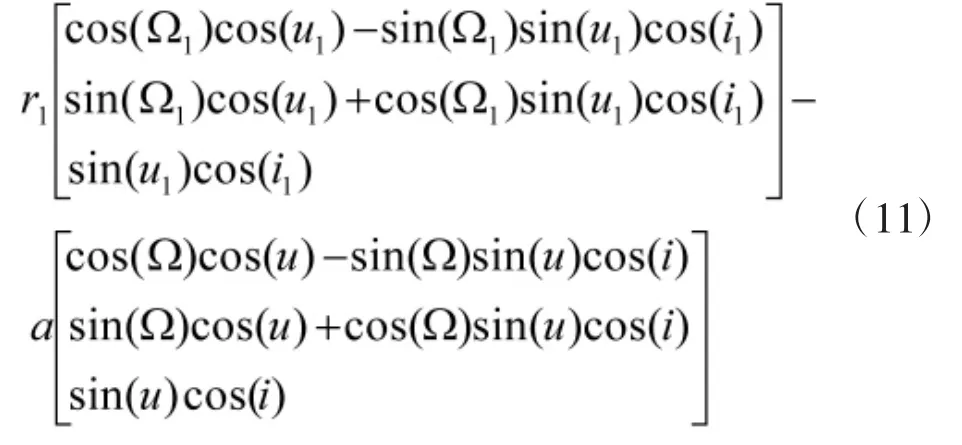
其中，

由于伴随卫星运动于圆轨道上，因此e=0，可以Hill方程推导绕飞轨迹方程为：

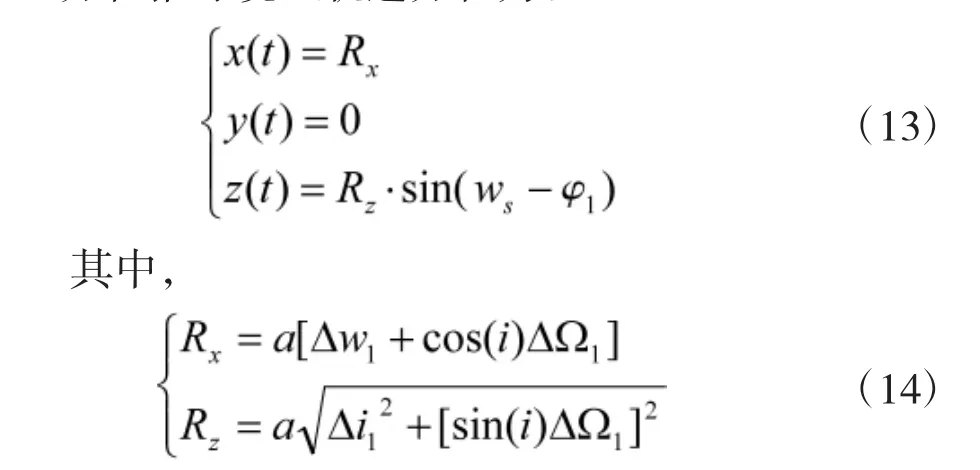
式中，φ1为B在摆动编队的初始相角，ws为摆动编队的平均角速度，Rx表示沿参考目标飞行方向B相对于参考目标A的距离，Rz表示B沿着垂直参考目标A轨道平面方向作简谐运动的幅度。钟摆编队有：

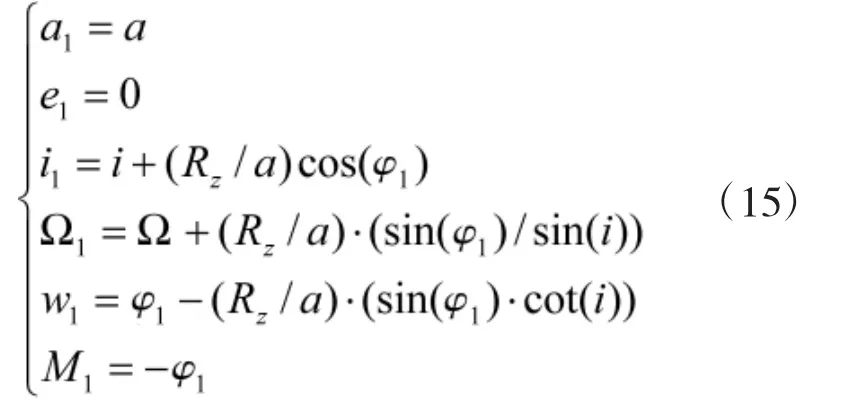
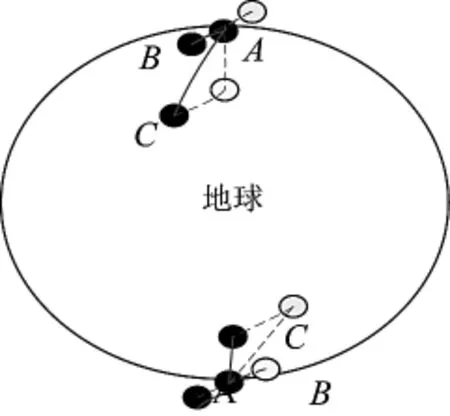
图2 悬挂轨道摆动编队示意图

图2所示，航天器C的轨道是参考目标A的轨道的悬挂摆动轨道。参考空间虚拟飞行器B的轨道半径为a1；航天器C的轨道半径为a2，f为其轨道半径的差。

根据悬挂轨道的定义，空间虚拟飞行器B和航天器C的瞬间运行角速度相等，航天器C的轨道六要素为（a2，i2，w2，Ω2，θ2），航天器的长半轴为

由于航天器C为圆轨道e2=0，航天器C与空间虚拟飞行器B相同轨道面因此轨道倾角相同，即

航天器C对空间虚拟飞行器B为悬挂轨道，根据其悬挂特性，航天器C与空间虚拟飞行器B轨道六要素除轨道半径不同，其他均相同。航天器的轨道六要素为（a2，i2，w2，Ω2，θ2）与参考目标A的轨道六要素关系为：

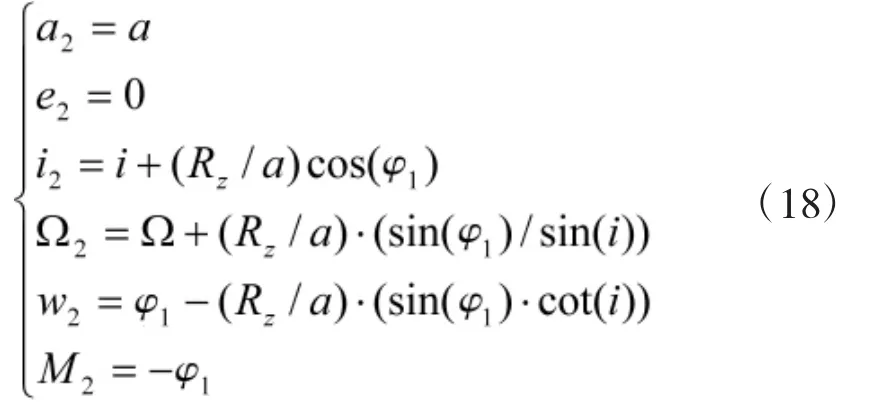
3 基于双脉冲机动的实现重构悬挂绕飞编队

根据特定任务，航天器由相对空间目标摆动绕飞编队重构形成摆动悬挂绕飞编队。虽然航天器的轨道与空间目标的轨道距离较近，但是航天器与空间目标的轨道不相同，因此，进行航天器编队重构转移，其转移过程如图3所示。

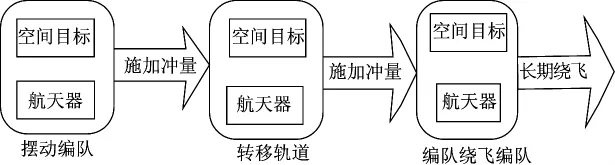
图3 轨道转移过程的框图

如图4所示，航天器C与空间目标A在t0时刻做摆动绕飞运动，航天器经过双脉冲机动后，在t1时刻航天器C与空间目标A悬挂式摆动绕飞。

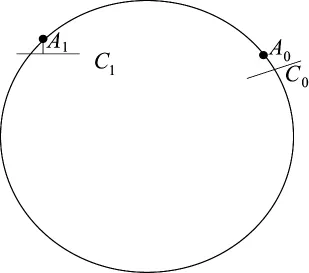
图4 轨道转移示意图

4 仿真模型的建立

航天器A和C的轨道六要素如表1所示，航天器C经过双脉冲冲量在9 000 s后，实现相对于航天器A的摆动式悬挂绕飞。

表1 航天器A和C的轨道六要素

控制过程的加速度同悬挂轨道，在STK中进行仿真如图5所示。

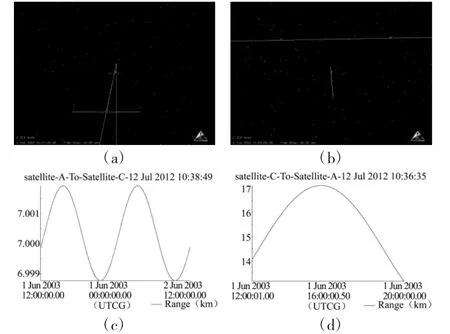
图5 悬挂摆动轨道应用模式

通过图5（a）中的视景仿真图和图5（c）航天器距离图可以看出航天器C对空间目标A做振幅为7 km的摆动绕飞。经过双冲量机动后，从图5（b）的视景仿真图和图5（d）航天器距离图可以看出航天器C在空间目标A的5 km下方作振幅为7 km悬挂式摆动绕飞。

6 结论

本文构建了一种基于编队航天器重构技术研究，对航天器双冲量机动方式进行了设计和实验。实验结果表明通过双冲量机动可以实现航天器编队重构，生成了STK编队重构视景仿真，进行了航天器编队重构计算和可视化服务研究。

［1］苏晏，黎康.卫星编队飞行相对轨道动力学模型的比较及选用［J］.空间控制技术与应用，2010，36（4）：54-58.

［2］赵军，蔡志勤，齐朝晖.基于平动点轨道的绳系卫星编队重构仿真［J］.系统仿真学报，2011，23（12）：2805-2812.

［3］袁建平.航天器轨道机动动力学［M］.北京：中科院研究生院，2010.

［4］杨帆，崔祜涛，崔平远.编队飞行卫星轨道的初步设计研究［J］.飞行力学，2005，23（2）：59-62.

［5］刘凯.基于相对轨道要素的卫星编队构型重构制导算法［J］.西北工业大学学报，2007，25（3）：374-377.

Research on Impulse Method of Spacecraft Formation Reconfigurable Control Simulation

LIU Meng1，CHI Yun2，ZHANG De-yu1
（1.Shenyang Ligong University，Shenyang 110159，China；2.Liaoning Academy of Govemance，Shenyang 110161，china）

Spacecraft Formation reconstructed for visibility is not strong，proposes to impulse a spacecraft formation reconstructed visual simulation technology.Double pulse motor is the transfer of the spacecraft space near orbit that it needs two impulse maneuver.Application of the principle of relative motion between the spacecraft，space target orbit six elements as the objective function space target by adjusting the orbital parameters of the spacecraft formation reconfiguration，swing around the fly transferred to swing hanging around the fly，and then come to the transfer of spacecraft the swing hanging around fly formation to the basic relationship of the impulse required to achieve control of the spacecraft space target formations reconstruction.

double pulse motor，relative motion，formation reconfigurable，swing suspension

TP391.9

A

1002-0640（2015）03-0167-03

2014-01-16

2014-03-22

刘 猛（1977- ），男，辽宁营口人，硕士，高级实验师。研究方向：嵌入式程序设计、分布式仿真技术。