水工结构工程分析计算方法回眸与发展

吴中如顾冲时苏怀智陈 波

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098；2.水资源高效利用与工程安全国家工程研究中心，江苏南京 210098）

水工结构工程分析计算方法回眸与发展

吴中如1，2，顾冲时1，2，苏怀智1，2，陈 波1，2

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098；2.水资源高效利用与工程安全国家工程研究中心，江苏南京 210098）

遵照《国家中长期科学和技术规划》中水利学科的水工结构工程创新前沿研究的要求，针对高坝与特高坝以及病险大坝的特点，讨论这些水工结构工程的关键问题及其存在的重大科学技术问题。重点针对应力分析、极限承载和非线性等关键科学技术问题，评述相关代表成果和研究进展，探讨了现行分析理论与方法的长处和不足，提出宏观、细观与纳观3层嵌套分析模型，微纳尺度分析法与随机疲劳理论等发展方向，以及水工结构工程科学中的应力分析、极限承载与非线性等健康诊断的综合分析理论与方法。

水工结构工程；大坝应力分析；大坝极限承载；大坝非线性；综述

我国人均水资源贫乏且时空分布严重不均，水资源主要分布在西南地区，为充分利用水资源和水能资源，兴建了大量水工结构工程。水利部和国家统计局公布的《第一次全国水利普查公报》表明，截至2012年底，全国共有已建、在建水库大坝98002座，其中大型水库756座，中型水库3938座，小型水库93308座，总库容9323.12亿m3，装机容量3.33亿kW［1］。这些水工结构工程在防洪、灌溉与供水、发电、航运等方面发挥了巨大的社会经济效应，是国民经济的重要基础设施。然而，这些水工结构工程存在以下主要关键问题：

a.大多数水工结构工程建于20世纪50—70年代，普遍存在防洪标准低、工程质量差等安全隐患，加上管理维护不善、工程老化等不利因素的影响，大量工程已为病险工程。据2006年全国水库大坝安全普查可知，病险水库大坝有3.7万座，且分布广、威胁大、病险工况复杂、险情重。病险水工结构工程不仅难以正常发挥工程效益，而且严重威胁人民的生命财产、其他基础设施与环境的安全，一旦溃决将产生毁灭性的灾难，如1975年8月石漫滩、板桥水库大坝溃坝和1963年8月刘家台水库溃坝等。因此研发新的实用可靠的水工结构分析理论与方法，对病险工程进行安全监控、预报与病险预警等十分重要。

b.我国西南地区存在大量的高坝水库，特高混凝土坝有锦屏一级（305 m）、小湾（294.5 m）、溪洛渡（285.5m）、白鹤滩（284m）等拱坝，特高土石坝有拟建的双江口（314m）和已建的糯扎渡（261.5m）心墙堆石坝［2］。这些大坝坝高200～300m，具有地形与地质极其复杂、地应力高、泄洪流量大等特点，设计、施工和运行等技术指标已突破了现行规范，需要利用安全监测手段和现代分析计算方法反馈与监控大坝安全工作性态，为制定新的水工结构工程设计、施工和运行规范提供技术支持。

c.水工结构工程安全是《国家中长期科学和技术发展纲要（2006—2020年）》中“重大自然灾害监测与防御”的重要内容。我国大型水电工程开发将在21世纪50年代基本结束，今后将主要转为运行管理。水工结构工程的安全分析与评价、病险水库大坝的补强加固、运行寿命诊断和退役或改建等将成为水利学科的研究重点。因此，基于运行多年的水工结构工程的大量监测资料发展现行水工结构的强度、稳定与耐久性和非线性等分析理论和方法很有必要。

d.随着信息科学的发展和智能分析技术的进步，水工结构工程分析计算领域的大数据和智能化特点越加突出，信息采集、传递、存储、计算、展示等流程的效果和效率进一步优化，这为实现水工结构工程安全的智能分析与决策提供了良好的技术支持。此部分内容将另行撰文阐述。

针对上述关键问题及其科学技术，笔者首先评述上述领域的代表性成果和研究现状与进展，然后提出研究发展方向。

1 水工结构工程分析计算的研究现状

1.1 高坝与特高坝应力分析

1.1.1 混凝土坝的应力分析

1.1.1.1 现行规范法及其改进

在重力坝与拱坝设计的现行规范［3-6］中规定，重力坝、拱坝分别采用材料力学法、拱梁分载法进行应力分析，并给出了相应的强度安全标准。但对于1～2级水电工程或结构复杂的重力坝、拱坝，这2种方法的误差较大，需要采用有限元法或模型试验加以验证或相互验证。因此，一些学者基于有限元法计算的应力推求内力，并采用材料力学公式反求等效应力［7］。等效应力可以消除应力集中现象，还能反映坝体断面的总体应力水平，从某种意义上解决了有限元法分析中应力数值的不稳定问题。但是，它是一种粗略的取值方法，掩盖了如局部应力集中可能导致一些开裂误判等的特殊问题。另外，虽然最大等效应力比最大有限元应力小，但等效应力的拉应力区范围比有限元应力的范围大。从这一点来说，有限元等效应力法建议的方法和以拉应力分布相对宽度作为控制标准的方法间存在矛盾，不能统一。因此，有限元法分析中应力取值一直是坝工界长期关注而又未很好解决的关键问题之一。DL／T 5346—2006《混凝土拱坝设计规范》［6］规定，对于200m以上的高坝，其拉应力控制标准应专门研究。以上应力分析方法及其控制标准是建立在一定的应力分析方法基础上的，两者必须配套。

1.1.1.2 有限元法

20世纪70年代起，我国水利水电系统推广采用有限元法［8］计算混凝土坝坝体应力，分析各种水工建筑物在不同动力荷载和静力荷载组合作用下的应力、变形和稳定等问题。实践证明有限元法计算灵活、适用范围广，对解决复杂结构与地质上大坝的基础应力及变位问题具有显著优点，亦为分析坝体内局部应力与分布，如坝内孔洞、角缘应力集中等问题提供了简捷方法，故在混凝土坝设计规范中明确规定了对于坝内设有大的孔洞、地质条件复杂的高坝应力，除用材料力学法与拱梁分载法计算外，还应进行有限元法或结构模型试验加以验证。在混凝土坝设计规范中还规定有限元法计算应力时以拉应力宽度作为控制标准。但是，至今有限元法仍难以以定量方式纳入混凝土坝设计规范，究其主要原因：（a）有限元法计算的应力受网格单元剖分的影响较大，应力解答具有不确定性，这是该法难以解决的问题。（b）没有与该法配套的安全标准，无法判断计算结果是否安全、合理。鉴于上述主要原因，有限元法在坝工设计中受到限制。为此，需要进一步研究有限元法在水工结构应力分析中的应用，尤其是精确求解应力分布问题。

1.1.1.3 有限元法的改进

有限元法的改进中，较为典型的是无单元法［9］，该法采用节点信息及局部支撑域上的权函数实行局部精确逼近，然后通过配点法或伽辽金法对偏微分方程求解，从而摆脱了单元的束缚。目前流行的无单元法是无单元Galerkin法类，它以最小二乘法构建插值基函数，从微分方程的弱变分形式原理出发，导出求解问题的代数方程；该类方法的特点是求解精度较高，但计算量大，需要背景网格（background cell）作为数值积分的积分域。另一类是基于配点型的无单元法，它以径向基函数来逼近场函数，直接在离散点上满足微分方程或边界条件，建立求解问题的代数方程。无单元法主要依靠形函数逼近来实现，形函数揭示了各类方法的逼近本质。理论上，固体力学无单元法对于三维非线性问题是可行的，但需要寻找合适算法来减少巨大的计算量。如在分析拱坝与坝基相互作用等大尺度问题时，可选用小波函数以减少节点数而又不影响计算精度。

1.1.1.4 混凝土坝应力仿真分析方法

有限元法是目前混凝土坝应力仿真分析的常用方法。混凝土坝的施工方式和材料，尤其是高拱坝的应力大、混凝土标号高、水泥用量多等特点，导致温度效应将延续较长时间，这对大坝施工期与运行期温度场和徐变应力场的全过程以及温控防裂等三维仿真有限元分析提出了更高要求。特别对于碾压混凝土坝，由于薄层碾压浇筑，材料特性（包括热学和力学等参数）随着龄期的不同而不同等，因此仿真分析中的时间步长要短，计算时间总步数有的多达千万，当浇筑层数过多、浇筑时间长时会使计算量大幅度增加。针对碾压混凝土坝三维仿真分析难度较大的特点，人们提出了一系列计算方法，如扩网并层算法、非均质单元法、波函数法、三维有限元浮动网格法和非均质层合单元法等。

1.1.2 面板堆石坝应力分析

通常采用3种方法研究面板堆石坝的应力变形性状，即模型试验法、有限元法和原型监测法，其中有限元法可模拟面板堆石坝施工及蓄水时的应力与变形性状。面板堆石坝坝体的应力与变形分析成果［10-12］主要归纳如下：

a.面板堆石坝的数值计算方面。堆石材料的本构模型必须能真实反映其非线性的应力与应变关系，尤其是徐变问题，线弹性模型不适用于计算堆石变形。目前面板堆石坝的应力、变形计算广泛采用以邓肯-张E-B模型［13］为代表的非线性弹性本构模型和以南水双屈服模型［10］为代表的弹塑性本构模型。其中，邓肯-张模型的弹性模型是应力状态的函数，可以描述堆石料应力应变关系的非线性和剪缩性，但该模型的参数间有一定的相关性，在应用时应注意其参数的协调性。众多面板堆石坝安全监测资料表明，采用这两类本构模型预测坝体应力和变形，与实测值仍有一定的差距。

b.在面板堆石坝的有限元分析中，面板与堆石体的接触，宜采用薄层接触面单元；混凝土面板之间的接触，宜采用分离缝单元；而面板与趾板之间的接触，宜采用软单元。这样的模拟方式，基本上考虑了面板堆石坝界面接触中的主要因素，在大多数情况下均可得出较满意的计算结果。而对于面板堆石坝界面接触的更精确模拟，可以采用界面单元方法，该法可以有效地处理接触面和接缝界面的滑移与分离问题。

c.为解决计算得到的面板堆石坝中面板和防渗墙拉应力值过大问题，采用折线型面板代替直线型面板来减小面板上的拉应力，采用圆弧型防渗墙代替常规的直线型防渗墙来减小防渗墙的拉应力，可以改善面板和防渗墙的应力状态。

d.堆石流变对面板的应力影响比较显著，高面板堆石坝尤为明显，一是堆石流变使面板沿坡向压应力增大，拉应力减小；二是堆石流变使面板河谷部位坝轴向压应力增大，岸坡拉应力增大，堆石流变使面板沿坡向趋于受压，有助于减小该方向上的拉应力，但坡向压应力有较大增加，在设计施工中，应给予足够的重视，并采取相应措施。

1.1.3 土石坝应力分析

土石坝的应力和变形计算有多种方法，主要有弹性理论方法、极限平衡理论方法、弹塑性分区方法、弹塑性差分方法、碎块体理论、工程软件法、有限元法等。其中有限元法是最常用的方法，采用有限元法计算应力应变时，土体的本构模型是关键。工程中常用的本构模型如下：

a.线弹性模型。该模型计算简单坝具有简易、方便等优点，且能够得到较满意的计算结果。但对较复杂的坝体，模型有明显的不足。所以，该模型尚未得到广泛应用。

b.K-G模型［14］。该模型同时考虑了土的剪切和压缩性质，理论相对完善。不足之处是确定K、G参数的试验比较复杂，工作量比较大。

c.推广的双曲线模型。该模型考虑的因素较多，理论比较完整，需要的试验不太复杂，相比其他模型具有明显优势。但是，模型比较复杂，参数较多，考虑了驼峰的剪切曲线和剪胀曲线后，需要确定相应的残余强度和极限剪切体变，在实用上还存在较多困难。

d.邓肯-张模型［15-16］。该模型模拟了土石体的主要特征，发展较早，工程应用经验成熟，各个参数有明确的物理意义和丰富的经验数值，是分析岩土工程的重要模型之一。

综上所述，土石坝数值分析计算常采用有限元计算方法、邓肯-张本构模型等，基本上能模拟土石坝施工时的应力变形过程。

1.2 高坝与特高坝的极限承载分析

极限承载包括稳定性与耐久性等，以往普遍以稳定性来控制，忽略了耐久性。因此评述研究成果时，重点评述稳定分析的成果。

1.2.1 大坝抗滑稳定分析方法

大坝的抗滑稳定十分复杂，其主要是分析坝体与基岩软弱结构面抗滑稳定安全度。近年来，随着各种勘测、处理技术和岩石力学的进展，抗滑稳定分析也取得了一定进展，但尚未形成统一的方法和明确的规定，需要凭借工程经验作出判断。目前大坝抗滑稳定分析方法包括刚体极限平衡法、有限元法、可靠度分析法和分项系数法等［17-20］。

a.刚体极限平衡法是依据勘测与设计经验先设定滑动面，将可能的滑动体（指坝体、岩体、或大坝与岩体组成的滑动体等）视为一个或若干个整体滑移的刚体，忽略其变形与滑裂面上的应力分布，仅考虑滑裂面上在各种荷载组合作用下的合力及其分力（正压力与剪应力），并忽略各个分力对滑裂面形心的力矩。依据勘测和工程经验设定滑动面上的抗剪强度（c、φ值等），计算滑动面上的滑动力与抗滑力及其比值（安全系数），然后根据安全系数判断滑动体的稳定安全度。该法常用剩余推力法、被动抗力法和等安全系数法计算安全度。当滑动面为单一滑裂面、参数（c、φ值等）符合实际情况时，因其有规范所定的安全系数标准，所以工程设计中应用较广泛；但当滑动面复杂、参数不确定时，该法忽略了某些控制性因素，结果将不符合实际情况。

b.有限元法。近年来，有限元法已广泛应用于对刚体极限平衡法的补充。有限元方法主要用点（或局部）抗剪安全系数Ke、抗滑富裕系数Ks、超载安全系数Kp、强度储备安全系数Kf和混合安全系数等分析大坝的抗滑稳定。同时，该法可分析计算：（a）坝体及地基内各点的应力与变位，沿软弱面上的局部安全系数，并据此估算整体抗滑系数；（b）分析在抗力体中的应力方向、应力大小和变位值，以及上游基岩中的拉应力数值和范围；（c）了解破坏区的分布、范围，找出最危险的部位及其严重程度；（d）分析各种加固措施的作用等。对于一些重要的工程，特别是抗滑稳定问题较严重时，除刚体极限平衡法外，常用有限元法与模型试验进行验证。但是有限元法也存在如1.1.1.2节所提及的问题。

c.可靠度分析法。该法是基于概率统计理论的不确定分析方法。基本思路：将影响大坝稳定的各种因素均作为随机变量进行统计分析，然后用结构分析方法建立大坝的失稳模式与极限状态方程。大坝的可靠度采用功能函数来反映：

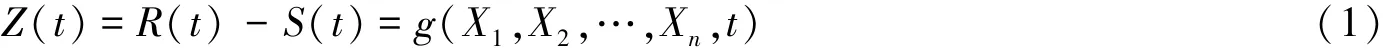
式中：Z（t）——大坝可靠度，Z（t）＞0表示大坝稳定可靠，Z（t）＜0表示大坝失稳破坏，Z（t）=0表示大坝抗滑稳定处于临界状态；R（t）——大坝自身抗力的随机变量；S（t）——大坝承受荷载效应的随机变量；t——时间；g（X1，X2，…，Xn，t）——表示大坝可靠度的功能函数。

假设荷载和抗力服从正态分布关系，满足R～N（μR，σR）和S～N（μS，σS），则大坝的失稳概率可表示为

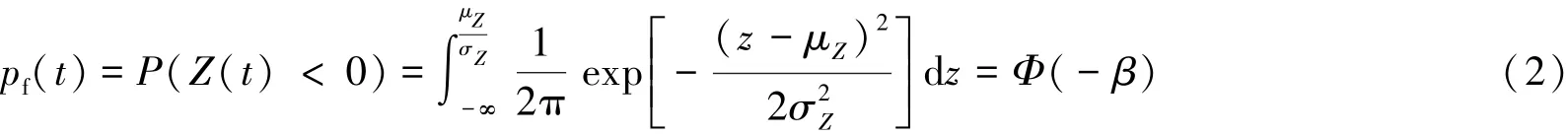
式中：β——可靠指标，当β＜βT时结构失效，其中βT为目标可靠指标。

由式（2）可得到某一时刻大坝的稳定可靠度，具体步骤如下：首先根据大坝可能的破坏模式，建立功能函数（式（1）），然后搜集各随机变量资料，确定统计参数，根据式（2）计算大坝抗滑稳定可靠度。

图1 R、S概率密度函数曲线Fig.1 Curves of R and Sprobability density functions

图1为R和S的概率密度函数曲线，在两曲线的重叠区内，如果R＜S，则结构失效。可靠度分析法将结构的抗力与荷载效应紧密联系（即极限状态方程），又考虑了各种主要参数之间的相关性与各自的随机性，因而比单一的安全系数法更反映实际情况，已逐渐应用于实际工程中。但该法中的极限状态方程难以表达为显式函数，给实际计算带来困难；同时，随机变量和不确定因素的分布对计算结果有较大影响，因而需要大量的试验资料，但在实际工程中往往很难获得足够多的样本，只能凭经验取值来推求一些变量的概率分布，使得计算精度降低。

d.分项系数法是DL 5108—1999《混凝土重力坝设计规范》［4］提出的验算坝体与基岩稳定性的方法，它将抗滑稳定分析从传统的安全系数表达式转化为极限状态表达式。采用分项系数和基本变量表征材料强度和计算方法等引起的不定性和变异性。分项系数法与传统的单一安全系数或多项系数设计方法有本质不同，它的各种分项系数都是根据可靠度理论与可靠指标优选而来。采用该方法的计算结果隐含反映了规定的可靠度水平，这也是现行规范推荐的方法，但也存在可靠度分析的一些具体困难。

e.稳定分析的其他理论和方法。有限元法在稳定分析中存在一些问题，如在大变形的仿真分析中，拉格朗日法的有限元网格可能产生扭曲，单元的雅可比行列式也可能为负值，这不仅会引起计算中网格重构，而且严重地影响解的精度。近几年，人们提出了一些新的分析理论和方法，如石根华［21］、沈振中等［22］提出的块体单元法和不连续变形分析法。

块体单元法假定岩体范围内共有n块可动块体单元，基于第i个块体单元在整体坐标系下的位移和形函数，列出该块体的平衡方程。对于每一个可移动块体单元，都可以建立一个平衡方程，将其集成，得到块体单元法的整体平衡方程。块体单元法认为复杂边坡一般由多种岩体组成，而岩体又被断层、节理、裂隙、层面以及软弱夹层等结构面切割为许多岩块，在组成岩体的许多岩块中，必定有一块安全系数最小，在各种力作用下首先滑移的一个岩块，然后其他岩块随之滑移，进而产生连锁反应，最后造成整体破坏。首先滑下的岩块称为关键块体，关键块体稳定与否，决定着岩体的稳定性。

不连续变形分析法考虑块体平移、转动、正应变和剪应变变形的情况，取块体系统的全一阶位移模式，块体系统的总势能包括块体单元的应变能以及初始应力、点荷载和线性荷载、体荷载、锚杆连接、惯性力和黏性力等势能。由最小势能原理，在势能泛函取最小值时系统达到平衡，建立系统的整体平衡方程。不连续变形分析法将每一个完整的块体作为一个单元，将节理、裂隙、断层等构造面和不同材料分区的界面等作为块体的边界，块体与块体之间用法向弹簧及剪切弹簧连接，从而将被不连续面所切割的块体系统连成一个整体进行计算。块体与块体之间的接触力，即法向及剪切弹簧上的力能较精确地满足平衡条件，由法向力与切向力、摩尔-库仑准则可以较精确地求出沿软弱面或不连续面的抗剪断安全系数分布。不连续变形分析法在模拟大坝的破坏过程方面也有较强的能力，因此是一种有发展潜力的方法。

1.2.2 评判大坝抗滑稳定安全性的标准

在大坝抗滑稳定分析时，会涉及确定失稳判据的问题，常见的失稳判据如下［23-24］：

a.收敛性判别标准。对大坝进行非线性有限元分析时，在荷载施加的某一个过程中，出现大坝变形不收敛现象，由此认为大坝达到了极限状态，此时的强度储备系数与超载安全系数可作为大坝抗滑稳定安全系数。

b.突变性判断准则。当大坝状态发生突变时，大坝从一个平衡状态向另一个平衡状态的转变，表示大坝性态发生了突变，一般可认为是突变标准，据此可以作为大坝的失稳判据。常用的突变特性：（a）大坝荷载变化或强度折减时，特征点的位移随之变化时的突变；（b）大坝关键部位位移变化率的突然变大；（c）塑性区发展成一定的滑动通道；（d）大坝结构中外力所做的功与形变势能不平衡。

c.最大弹性变形能判别标准。通常用于判别大坝与地基系统达到极限平衡状态的位移判别量是局部量，其量值往往随着位置的变化产生较大差别。因此，利用弹性变形能这类系统的整体量来度量大坝极限承载能力，将弹性变形能达到最大值作为系统失稳的判别标准是今后的一个研究方向。

综上分析，抗滑稳定性分析方法较多，各种方法互有优缺点，没有一个公认的最佳方法，失稳判据也存在相同的问题。因此，今后研究的重点是确定最佳抗滑稳定方法及其相应的失稳判据。

1.3 高坝与特高坝非线性问题

高坝的非线性主要包括几何非线性、材料非线性和时间非线性。几何非线性主要包括高坝的损伤和裂缝等，材料非线性主要是材料的塑性等，时间非线性主要是徐变与流变等。高坝和特高坝同时存在几何非线性、材料非线性与时间非线性。

1.3.1 大坝损伤分析

从宏观角度分析，大坝的破坏经历了弹塑性、断裂和破坏3个阶段。融合损伤力学与断裂力学，建立考虑损伤的断裂力学，称为破坏力学。损伤力学主要研究出现宏观裂纹之前材料中分布的细观缺陷的发展演化；而断裂力学则研究出现宏观裂纹之后的扩展和含宏观裂纹变形体的力学性能，忽略在宏观裂纹形成以前的损伤阶段，也忽略了宏观裂纹周围的损伤，只考虑理想的宏观缺陷。因此，断裂力学与损伤力学应当互补，尤其在上述过渡阶段，急待将损伤力学和断裂力学相融合，形成分析过渡阶段的损伤与断裂前兆的方法。在这方面，模糊裂纹模型和钝裂纹带模型可作为参考模型［25-26］。

20世纪70年代前后创立的耗散结构论、协同论、突变论、混沌、分形及超循环理论等，构成了现代非线性科学的理论体系，为识别复杂现象提供了新的思维方式。被誉为20世纪继量子力学和相对论后的第三次科学革命，并成为新世纪科学发展的主要方向之一。在研究混凝土等脆性材料损伤破坏力学中，一些学者敏锐地提出了分析非线性特征的突变论、协同论和耗散结构理论等现代非线性理论，为重新认识材料的损伤破坏过程提供了新的思路。

1.3.2 混凝土坝裂缝分析

1.3.2.1 基于断裂力学的裂缝分析方法

目前，常用断裂力学分析判断裂缝是否发生转异而失稳。最早将断裂力学用于混凝土研究的是Kaplan［27］，他将金属断裂力学理论用于分析混凝土裂缝。越来越多的试验表明，断裂韧度Kc、临界能量释放率Gc及断裂能GF等断裂主要判据不仅依赖于试件大小，还依赖于几何条件，随试件尺寸的变化而变化。应用线弹性断裂力学的一个主要条件是材料为均质连续和各向同性的弹性体，而混凝土则是一种非均质多相复合材料。有些学者在混凝土断裂试验中发现，在扩展演变过程中，混凝土呈现某种程度的非线性，据此认为混凝土并不是脆性材料，而是弹塑性材料。因而倾向于用弹塑性断裂力学参数作为混凝土断裂特性的判据［28-29］。研究表明，混凝土断裂力学参数存在明显的尺寸效应，且试验结果相互矛盾，因此妨碍了断裂力学在混凝土坝裂缝诊断中的应用。在混凝土坝裂缝扩展演变分析方面，一些学者提出了相应的数值模型［30-31］，并进行了数值模拟分析。

目前，国内外学术与工程界对混凝土断裂的研究虽取得了一些进展，但对裂缝发展演变的数值模拟还存在很大困难，特别是非线性材料、各向异性、复杂受力状态的裂缝失稳等还难以解决。

1.3.2.2 应用非线性理论研究混凝土坝裂缝演变规律

带缝大坝与库水和坝基相互作用时，系统具有内在的不确定性，加之外部环境（如气温、降雨、地震等）等多种因素的影响，使大坝处在一个复杂的时空系统中，具有显著的非线性特征。由于应用断裂力学分析混凝土坝裂缝演变规律遇到了较大困难，因此许多学者［32-34］探索用非线性理论对裂缝突变规律进行挖掘、分解、解释和预测等。

1.3.3 大坝黏塑性分析

根据大坝安全细则和监测规范，大坝的安全状态一般分正常、异常和险情三大类；大坝的结构性态也可以相应地分为黏弹性、黏弹塑性和失稳破坏3个工作状态。因此，大坝安全监控指标［24］相应地分为一级、二级、三级，一级和二级安全监控指标已应用到实际工程。

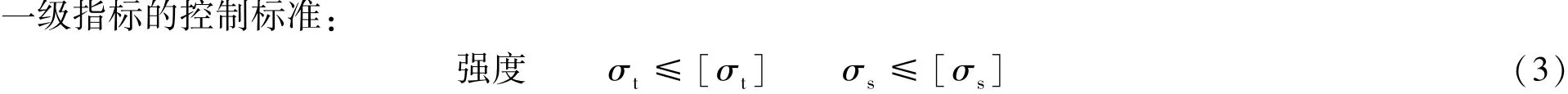
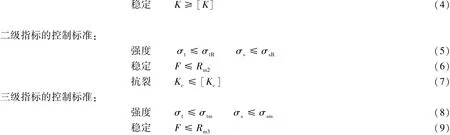
式中：σt、σs——不利荷载工况下在控制部位的拉应力和压应力；［σt］、σtR、σtm——允许拉应力、屈服强度和强度极限；［σs］、σsR、σsm——允许抗压强度、屈服强度和强度极限；F——对应不利荷载组合时，滑裂面上的滑动力；Rm2、Rm3——对应滑动面处于屈服和强度极限时的抗滑力；K、［K］——对应不利荷载组合时的抗滑稳定安全系数和允许抗滑稳定安全系数；Kc、［Kc］——裂缝尖端的应力强度因子和断裂韧度。

在一级监控状态下，高混凝土坝坝体任一点的应力均未超过材料的比例极限，坝踵拉应力小于允许值，坝体处于黏弹性工作阶段（图2中A点之前）；或者坝踵区部分开裂，应力重新调整，下游区压应力增加但仍在比例极限以内，应力与应变关系基本呈线弹性或黏弹性，坝体处于准黏弹性阶段（图2中B点之前）。在该状态下，拟定安全监控指标时，坝体和基岩的本构模型分别采用伯格斯模型和广义开尔文模型。

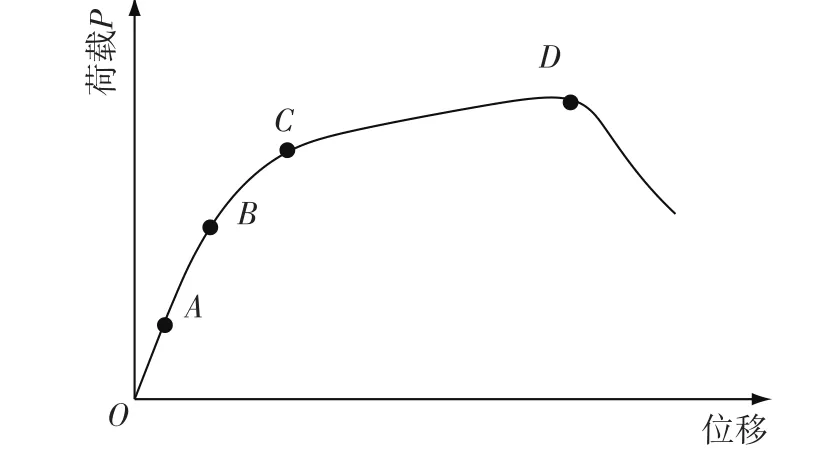
图2 荷载与位移关系Fig.2 Relationship between load and displacement

在二级监控状态下，裂缝区扩展，下游区压应力增加，进入屈服状态，结构的变形有较大增加，应力与应变开始呈非线性，坝体处于黏弹塑性状态（图2中C点之前）。此时，坝基和坝体宜用6参数的弹-黏-黏弹-黏塑性模型［24］。

2 水工结构工程分析计算的发展方向

基于高坝及特高坝的应力分析、极限承载与非线性等研究现状与有待进一步研究问题的综述，针对高坝、特高坝以及病险大坝的结构特点，提出了今后研究的发展方向。

2.1 高坝与特高坝应力分析

2.1.1 混凝土坝

a.在有限元法方面，发展由误差分析自动调整的自适应算法，以提高求解过程中分析成果的可靠性和精度。

b.采集足够多样本资料，对其等效应力和实际应力分布与裂缝开展情况进行综合分析研究，用概率统计的方法确定具有一定安全度的等效应力控制指标。

c.进一步研究更加合理有效的应力仿真分析方法。

d.三维结构仿真模型试验［35-36］也是高坝与特高坝应力分析的重要方法，它可以分析复杂坝型的应力与变形及其分布，揭示大坝变形和破坏的机理。与此同时，可以提高有限元法分析的可靠性和精度，如由模型试验测得的应力为依据，校准与优化有限元网络与算法等。

2.1.2 面板堆石坝

a.试验研究：离心模型试验与数值计算分析相结合是有效的方法。在离心模型试验中，应分析模型试验中的固有误差，发展仿真模拟面板材料、堆石材料缩尺、试验数据采集与传输、内部变形、蓄水过程等新技术。在室内试验中，仿真模拟堆石体的流变特性、面板与垫层之间和防渗墙与墙两侧砂砾石层等相互作用、接缝的应力变形特性，以提出更合理的本构模型及参数。

b.采用更合理的本构模型，在有限元模型中真实模拟混凝土面板与垫层接触面、接缝面板与混凝土防渗墙加载过程及网格划分等。

c.充分利用已有的原型监测资料，运用反分析方法，对现有模型进行检验和修正，并获得较为可靠的参数，使面板堆石坝应力、变形与稳定分析等定量分析成果更好地为工程服务。

2.1.3 土石坝

a.研究更合理的岩土本构模型，目前的岩土本构模型尚难以全面反映岩土体的各种性质，限制了数值分析计算的发展。

b.目前计算参数多数基于三轴试验，虽表征了岩土体的部分力学性质，但应用于各向异性的岩体时，仍有一定的局限性。另外，颗粒土的尺寸效应对计算参数的影响有待进一步研究。

c.水库蓄水后，由于水的渗透作用，土石坝的后期应力与变形比施工填筑期更为复杂，影响因素更多。因此，需要进一步研究土石坝的后期变形。

d.当坝基布设混凝土防渗墙时，由于混凝土防渗墙与坝基土层模量相差悬殊，防渗墙与周围土层难以满足变形协调条件，需要进一步研究界面接触模型。

2.1.4 大坝应力分析新理论

高坝和特高坝具有应力大、应力水平高以及危害性裂缝多等特点，以往的应力分析理论和方法难以分析宏观、细观与纳观耦合的应力应变，需要探索融合微纳米尺度的宏观、细观与纳观3层嵌套的力学模型，据此分析应力应变与裂缝的稳定性，其基本原理：（a）用原子镶嵌模型和分子动力学理论模拟裂纹尖端附近的纳观区行为；（b）用弹性基体加离散位错描述细观区行为；（c）宏观区采用超弹性／黏塑性大变形本构关系和有限元计算。有些学者［37-39］提出了新的MD（分子动力学）-MPM（材料点方法）-HS跨尺度计算模式，在跨尺度计算中，关键区域（如裂纹尖端）采用分子动力学来模拟，其他非关键区域采用连续介质力学模拟，连接区域把材料点看作原子并将其排列在实际晶格位置。

2.2 高坝与特高坝的极限承载分析

由于大坝通常存在软弱结构面，对大坝的变形、受力和稳定性有重要影响，因此抗滑稳定分析是大坝设计中的一个主要内容。与此同时，大坝长期在复杂环境中工作，大坝老化与耐久性问题越来越突出，因此需要进一步研究抗滑稳定和大坝耐久性的分析方法，需研究的问题主要归纳为以下几个方面：

a.刚体极限平衡法具有统一的稳定判断标准，能够求出单一滑动面和双斜滑动面的稳定安全系数。但是在双斜滑动面的理论公式推导过程中，传统算法均涉及了较多假设，对计算结果有较大影响。因此抛弃假定条件，对稳定安全系数的计算方法进行改进，可以提高计算结果的精确度。对存在多个滑动面的大坝，现有的方法难以分析稳定性问题，因此需进一步研究多滑动面稳定安全系数的分析方法。

b.目前广泛使用的有限元法缺乏统一的稳定安全判据，进行稳定性判断时带有较大的主观性，因此需要进一步研究有限元法的稳定判据。DDA、NMM、Meshfree Method等新兴数值方法尚处于初步研究阶段，在高坝与特高坝稳定分析中具有很大的应用潜力。进一步发展地质力学仿真模拟模型试验，并与数值分析有机融合，是研究高坝与特高坝极限承载能力的有效途径。

c.进一步加大对高坝与特高坝耐久性问题的研究，以往在建设中通常用强度与稳定控制，忽略了耐久性的控制。为此，要加大耐久性的研究，其中混凝土坝除重点研究裂缝外，还应研究溶蚀、碳化、腐蚀与碱骨料反应等；土石坝应研究岩土体的流变、渗透变形（管涌和流土）的机理与规律等。

2.3 高坝与特高坝非线性问题

a.混凝土力学特性具有纳观与细观非均质性导致的非线性。只有摆脱传统线性分析的约束，寻求非线性分析理论与方法，结合系统论、控制论、信息论等先进理论，正确揭示材料损伤的破坏机理，才能使混凝土非线性力学的研究进一步发展。

b.任何水工结构工程，尤其是高坝与特高坝的疲劳破坏过程大致都经历4个时期，即疲劳成核期、微观裂纹增长期、宏观裂纹扩展期以及最后断裂期。在工程实践中，为了简化计算，常综合为2个阶段，即疲劳裂纹形成阶段和疲劳裂纹扩展阶段，也即微观与宏观之分。因此，需进一步探索用微纳米尺度的力学分析方法（宏观、细观、纳观3层嵌套的力学模型）分析裂缝和强度。

c.随机疲劳理论是今后研究的重要方向，为此要融合随机过程理论、模糊数学理论等新理论，使处理疲劳问题更加符合实际情况。结构疲劳是一门实验科学，同时要结合其他理论对疲劳理论进行完善，为较准确地计算水工结构工程的全寿命及其可靠性以及高坝与特高坝的设计、施工与运行提供科学依据。

d.发展几何非线性问题的分析理论与方法。裂缝是大坝安全的主要危害，需要利用实测数据，结合数值模拟分析和物理模型试验，融合断裂力学基本概念和非线性理论，研究裂缝发展演变过程的耗散结构特征，构建基于分形几何裂缝扩展演变分形方法，建立混凝土坝裂缝扩展演变的熵变理论与方法体系，并探索基于非线性理论的裂缝转异诊断方法。

e.材料、几何与时间3种非线性的耦合分析。在高坝与特高坝非线性中，这3种非线性关系同时存在，在确定高混凝土坝二级安全监控指标时，可将材料的断裂考虑到坝基和坝体的本构模型中，建立坝基与坝体的7参数（弹-黏-断-黏弹-黏塑性）本构模型；同时，还要深入研究高面板堆石坝的堆石体徐变对大坝强度、稳定安全的分析理论和方法。

3 结 语

a.我国多数水工结构工程建于20世纪70年代以前，由于多种原因存在老化病变问题。水工结构工程的设计、施工和运行规范多数在20世纪80年代前制定，由于当时的科学技术水平限制和工程实践等问题，其技术规范不能适应已建和待建的200～300 m特高坝的设计、施工、运行和大量病险大坝的健康诊断等需要。亟待总结已建水工结构工程的多年运行经验与教训，针对高坝与特高坝和病险大坝的特点，对水工结构工程科学中的应力分析、承载能力和非线性等关键科学技术问题进行深入研究，在评述现有代表性成果基础上，探索实用的新理论与方法，为已建大坝的健康诊断与病险工程处理以及高坝与特高坝的建造提供技术支持。

b.在应力与承载能力（稳定）分析中，以往主要沿用设计、施工和运行规范的方法。本文评述了上述分析理论与方法的优点与不足，提出了研究方向和解决思路，探索了宏观、细观与纳观3层嵌套分析模型以及稳定分析的新理论与方法。

c.在非线性分析中，由于以往大坝与坝基设计的控制应力较小或应力水平较低，强度与稳定安全度较高，所以对大坝的非线性问题尚缺乏有关技术规范。然而，对高坝与特高坝的大应变或应力水平高等所引起的材料、几何和材料等非线性问题以及病险大坝的裂缝等非线性问题，以往不少学者虽做了研究，但是缺少统一的本构模型、分析理论与方法及其相应的安全判据。本文为此作了评述，提出了微纳尺度分析法与随机疲劳理论等分析理论与方法，探索了构建合理实用的本构模型与数值分析方法及其相应判据的途径。

d.融汇原位监测、模型试验与数值分析等理论与方法，提出了水工结构工程科学（尤其是高坝与特高坝和病险坝）中的应力、极限承载与非线性等健康诊断的综合分析理论与方法。

［1］张建云，杨正华，蒋金平，等.水库大坝病险和溃坝研究与警示［M］.北京：科学出版社，2014.

［2］水利部建设与管理局、水利部大坝安全管理中心.中国高坝大库TOP100［M］.北京：中国水利水电出版社，2012.

［3］SL 319—2005 混凝土重力坝设计规范［S］.

［4］DL 5108—1999 混凝土重力坝设计规范［S］.

［5］SL 282—2003 混凝土拱坝设计规范［S］.

［6］DL／T 5346—2006 混凝土拱坝设计规范［S］.

［7］朱伯芳.拱坝的有限元等效应力及复杂应力下的强度储备［J］.水利水电技术，2005，36（1）：43-47.（ZHU Bofang.Equivalent finite element stresses and safety of arch dams under triaxial stresses［J］.Water Resources and Hydropower Engineering，2005，36（1）：43-47.（in Chinese））

［8］杜平安，于亚婷，刘建涛.有限元法：原理、建模及应用［M］.2版.北京：国防工业出版社，2011.

［9］周维垣，黄岩松，林鹏.三维无单元伽辽金法及其在拱坝分析中的应用［J］.水利学报，2005，36（6）：644-649.（ZHOU Weiyuan，HUANG Yansong，LIN Peng.Three-dimensional element-free Galerkin method and its application in analysis of arch dams［J］.Journal of Hydraulic Engineering，2005，36（6）：644-649.（in Chinese））

［10］贾金生，郦能惠.高混凝土面板坝安全关键技术研究［M］.北京：中国水利水电出版社，2014.

［11］蔡新.混凝土面板堆石坝结构分析与优化设计［M］.北京：中国水利水电出版社，2005.

［12］朱晟.水布垭面板堆石坝施工与运行性状反演研究［J］.岩石力学与工程学报，2011，30（2）：3689-3695.（ZHU Sheng.Backanalysis on construction and operation properties of Shuibuya concrete face rockfill dam［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30（2）：3689-3695.（in Chinese））

［13］李炎隆，李守义，丁占峰，等.基于正交试验法的邓肯-张E-B模型参数敏感性分析研究［J］.水利学报，2013，44（7）：873-879.（LI Yanlong，LI Shouyi，DING Zhanfeng，et al.The sensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method［J］.Journal of Hydraulic Engineering，2013，44（7）：873-879.（in Chinese））

［14］NAYLOR D J.Stress-strain laws for soils，developments in soil mechanics［M］.Essex：Applied Science Publishers Ltd.1978.

［15］DUNCAN J M，CHANG C Y.Nonlinear analysis of stress and strain in soils［J］.Journal of the Soil Mechanics and Foundations Division，1970，96（5）：1629-1653.

［16］DUNCAN J M，BYRNE P M，WONG K S，et al.Strength，stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses（UCB／GT／80-01）［R］.Berkeley：University of California，Berkeley，1980.

［17］蒋春艳，常晓林，周伟.用于重力坝抗滑稳定分析的分项系数有限元方法［J］.水力发电学报，2006，25（2）：16-20.（JIANG Chunyan，CHANG Xiaolin，ZHOU Wei.Partial coefficient FEM for gravity dam anti-sliding stability analysis［J］.Journal of Hydroelectric Engineering，2006，25（2）：16-20.（in Chinese））

［18］周伟，常晓林，徐建强.基于分项系数法的重力坝深层抗滑稳定分析［J］.岩土力学，2007，28（2）：315-320.（ZHOU Wei，CHANG Xiaolin，XU Jianqiang.Analysis of anti-sliding stability in deep foundation of gravity dam based on partial coefficient［J］.Rock and Soil Mechanics，2007，28（2）：315-320.（in Chinese））

［19］任旭华.碾压混凝土重力坝的安全评价方法和安全标准的研究［J］.河海大学学报：自然科学版，1998，26（4）：8-13.（REN Xuhua.Study on safety assessment method and safety criteria of RCC gravity dams［J］.Journal of Hohai University：Natural Sciences，1998，26（4）：8-13.（in Chinese））

［20］刘先珊，周创兵，盛永清，等.高拱坝动力分析及坝肩稳定性研究［J］.岩石力学与工程学报，2007，26（增刊1）：3421-3426.（LIU Xianshan，ZHOU Chuangbing，SHENG Yongqing，et al.Dynamic analysis and research on abutment stability of high arch dam［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（Sup1）：3421-3426.（in Chinese））

［21］石根华.数值流形方法与非连续变形分析［M］.裴觉民，译.北京：清华大学出版社，1997.

［22］沈振中，马明，涂晓霞.基于非连续变形分析的重力坝变形预警指标［J］.水利学报，2007，38（增刊1）：94-99.（SHENG Zhenzhong，MA Ming，TU Xiaoxia.Early warning index of deformation for gravity dam based on discontinuous deformation analysis［J］.Journal of Hydraulic Engineering，2007，38（Sup1）：94-99.（in Chinese））

［23］任青文.灾变条件下高拱坝整体失效分析的理论与方法［J］.工程力学，2011，28（增刊2）：85-96.（REN Qingwen.Theory and methods of high arch dam's entire failure under disaster conditions［J］.Engineering Mechanics，2011，28（Sup2）：85-96.（in Chinese））

［24］吴中如.水工建筑物安全监控理论及应用［M］.北京：高等教育出版社，2003.

［25］何建涛，马怀发，陈厚群.混凝土损伤本构理论研究综述［J］.水利水电科技进展，2010，30（3）：89-94.（HE Jiantao，MA Huaifa，CHEN Houqun.Research review on concrete damage constitutive theory［J］.Advances in Science and Technology of Water Resources，2010，30（3）：89-94.（in Chinese））

［26］于海祥，武建华，李强.混凝土损伤本构模型研究评述［J］.重庆建筑大学学报，2007，29（2）：68-72.（YU Haiyang，WU Jianhua，LI Qiang.A review of concrete damage constitutive models［J］.Journal of Chongqing Jianzhu University，2007，29（2）：68-72.（in Chinese））

［27］KAPLAN M F.Crack propagation and the fracture of concrete［J］.Journal of the American Concrete Institute，1961，58（5）：591-610.

［28］ZHANG J，LI J.Elastoplastic damage model for concrete based on consistent free energy potential［J］.Science China-Technological Science，2014，57（11）：2278-2286.

［29］SHAH K R.Elasto-plastic crack growth in pressure sensitive materials［J］.ASTM Special Technical Publication，1999，9（7）：233-247.

［30］许青，邓涛，董伟.基于裂缝扩展准则的混凝土重力坝裂缝扩展全过程数值分析［J］.建筑科学与工程学报，2009，26（3）：49-54.（XU Qing，DENG Tao，DONG Wei.Numerical analysis of complete crack propagation process in concrete gravity dams based on crack propagation criterion［J］.Journal of Architecture and Civil Engineering，2009，26（3）：49-54.（in Chinese））

［31］寇晓东，周维垣.应用无单元法近似计算拱坝开裂［J］.水利学报，2000，31（10）：28-35.（KOU Xiaodong，ZHOU Weiyuan.The application of element-free method to approximate calculation of arch dam crack propagation［J］.Journal of Hydraulic Engineering，2000，31（10）：28-35.（in Chinese））

［32］OU J P，LI H，DUAN Z D，et al.A dynamic model for dam monitoring［C］／／佚名.Proceedings of the 2nd InternationalConference on Structural Health Monitoring of Intelligent Infrastructure.Shenzhen：A.A.Balkema Publishers，2005，11：1243-1246.

［33］GU Congshi，LI Zhanchao，XU Bo.Abnormality diagnosis of cracks in the concrete dam based on dynamical structure mutation［J］.Science China（Technological Sciences），2011，54（7）：1930-1939.

［34］BAO Tengfei，QIN Dong，ZHOU Xiwu，et al.Abnormality monitoring model of cracks in concrete dams［J］.Science China：Technological Sciences，2011，54（7）：1914-1922.

［35］周维垣，杨若琼，刘耀儒，等.高拱坝整体稳定地质力学模型试验研究［J］.水力发电学报.2005，24（1）：53-58.（ZHOU Weiyuan，YANG Ruoqiong，LIU Yaoru，et al.Research on geomechanical model of rupture tests of arch dams for their stability［J］.Journal of Hydroelectric Engineering，2005，24（1）：53-58.（in Chinese））

［36］杨强，刘耀儒，潘元炜，等.高拱坝稳定与控制理论及其试验验证［C］／／中国大坝协会.高坝工程技术进展.成都：四川大学出版社，2012.

［37］张楚汉，金峰.岩石和混凝土离散-接触-断裂分析［M］.北京：清华大学出版社，2008.

［38］杜修力，金浏.基于随机多尺度力学模型的混凝土力学特性研究［J］.工程力学，2011，28（1）：151-154.（DU Xiuli，JIN Liu.Mechanical property research on concrete based on random multi-scale mechanical model［J］.Engineering Mechanics，2011，28（1）：151-154.（in Chinese））

［39］李友云，郑健龙，崔俊芝，等.一类混凝土力学参数的迭代多尺度有限元预测方法［J］.计算力学学报，2010，27（1）：116-120.（LI Youyun，ZHENG Jianlong，CUI Junzhi，et al.Iterative multi-scale finite element predicting method for the elasticity mechanics parameters of the concrete with multi-graded rocks［J］.Chinese Journal of Computational Mechanics，2010，27（1）：116-120.（in Chinese））

Review and prospect of calculation analysis methods in hydro-structure engineering

WU Zhongru1，2，GU Chongshi1，2，SU Huaizhi1，2，CHEN Bo1，2
（1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China；2.National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety，Hohai University，Nanjing 210098，China）

In accordance with demands of theNational Program for Medium-and Long-term Scientific and Technological Developmentfor cutting-edge research on hydro-structure engineering，and in consideration of the characteristics of high dams，super high dams，and dangerous dams，significant scientific and technological problems in hydro-structure engineering are examined.Representative achievements and progress in research on stress，ultimate bearing capacity，and nonlinearity analysis are reviewed，and then the advantages and disadvantages of current theories and methodologies are analyzed.Finally，development directions，including the macro-meso-nano coupling analysis model，micro-nano scale analysis method，stochastic fatigue theory，and the comprehensive analysis theory and method for health diagnosis based on stress，ultimate bearing capacity，and nonlinearity analyses in hydro-structure engineering，are proposed.

hydro-structure engineering；dam stress analysis；ultimate bearing capacity of dam；nonlinearity of dam；review

TV314

A

1000-1980（2015）05-0395-11

10.3876／j.issn.1000-1980.2015.05.003

20150715

国家自然科学基金重点项目（51139001）；国家自然科学基金面上项目（51379068，51179066，51279052）；水利部土石坝破坏机理与防控技术重点实验室基金（KY914002）

吴中如（1939—），男，江苏宜兴人，中国工程院院士，教授，主要从事水工结构安全监控研究。E-mail：zrwu＠hhu.edu.cn