复铰式100%低地板车辆振动特性分析

2015-06-12孔新星肖守讷韦海菊

机械制造 2015年10期

□ 孔新星 □ 朱涛 □ 肖守讷 □ 韦海菊

1.西南交通大学牵引动力国家重点实验室成都 610031

2.南车南京浦镇车辆有限公司动车设计部南京 210031

近年来，我国城市轨道交通得到了飞速发展，截止到2014年8月，已有十个城市开通了城市轨道交通系统，运营里程2 746 km，到2015年预计达到3 500多km，而100%低地板轻轨车作为现代城市新型交通装备，具有造价低、节能环保、适应城市轨道交通线路的特点，是国家科技部“十一五”重点科技支撑项目，在我国具有很大的发展空间和广阔的市场应用前景。

低地板车辆与传统城市轨道车辆的区别在于为了方便乘客上下，车辆的地板面至地面的高度降低到350 mm左右，其动车和拖车转向架都采用了独立车轮的结构，在转向架的轴数、电机的悬挂形式、传动方式等的选择上呈多样化趋势。另外为了适应车辆的小曲线通过性能，车体各模块之间采用铰接的连接方式。因此，结构动力学与振动性能与传统轨道车辆相比相对复杂。常树民从低地板轻轨车的结构特点与承载特性出发，对车体设计和校核进行了介绍与分析；庞洁对低地板轻轨车转向架各部分结构振动强弱分布以及抗振薄弱区进行了分析；张杨等针对铰接车体转向架横摆稳定性进行了分析；池茂儒等对一种新型独立车轮低地板转向架曲线通过性能进行了研究。

现有的文献较多的是对低地板车辆车体、转向架的结构和动力学进行研究，对二者之间的耦合振动关系研究甚少。车辆结构振动特性对整个车辆性能有十分重要的影响，当所受激振力的频率与车辆结构某一固有频率接近时，就可能产生很高的动应力，造成车辆结构的强度破坏或产生不允许的大变形破坏车辆结构的性能。对复铰式低地板车辆，由于难以模拟铰接连接，因此，目前对于复铰式低地板车辆振动模态的研究，都是针对单模块，这种方法无法评价模块铰接成整车时的振动性能。笔者对一种由5节车体组成的复铰式低地板面的轻轨车辆作了振动性能分析,可为100%低地板轻轨车辆的自主设计做理论支撑。

1 模态计算理论

对于具有黏性阻尼的多自由度系统，在广义坐标上受同频率、同相位的正弦力作用下，系统的强迫振动微分方程为：

式中:M为系统质量；x为坐标系下的位移；C为系统阻尼；K为系统刚度；P为强迫振动的幅值；ω为振动频率。

采用正则坐标系下位移xn代替原有坐标系下位移x，建立正则坐标系下的强迫振动方程：

式中:I为正则坐标系下的系统质量；xn为正则坐标系下的坐标位移；Cn为正则坐标系下的阻尼；Kn为正则坐标系下的刚度，即：

式中：xnj为第j阶振型的正则坐标系下位移；Cnj为第j阶振型下正则坐标系下的阻尼；Pnj为第j阶振型的振幅。

又 Pn=AnTP，将式（3）改写为：

式中：ζj为第j阶振型的相对阻尼系数；ωj为第j阶振型的频率。

式（4）是一组互相独立的方程，均可以独求解，即：

式中：λj为第j阶振型的频率比；φj为强迫振动的相位与激振的相位之差

则系统在 Psin（ωt）下的响应为：

2 低地板结构特点及铰接模拟计算

2.1 低地板结构特点

某复铰式100%低地板轻轨车辆为5节编组形式。其中1、5模块为动车模块，2、4模块为悬浮模块，3模块为拖车模块。模块间采用铰接结构，车厢内地板面完全贯通，车门均安置在低地板区域,高度为320 mm，可以方便旅客上下车。车体的底部铰接全部为固定铰，限制X、Y、Z 3个方向的移动，固定铰承受了悬浮模块的垂向力，传递大部分的纵向力和横向力；闭合铰可以绕垂直轴旋转和移动，但是限制了其它4个方向的自由度，承受了部分纵向力和横向力；开放铰仅限制横向的移动，它只可以承受横向力。图1所示为某典型的复铰式100%低地板轻轨车辆。

▲图1 某复铰式100%低地板轻轨车辆

2.2 铰接装置的模拟

铰接装置的模拟是低地板整车模态分析的难点之一。笔者采用运动矢量链来模拟，即将关节视为无质量的运动约束，每一节车体相对基本惯性坐标均有运动连接关系。在有限元软件NASTRAN中使用具有运动约束功能的RJONT单元模拟相应的铰接装置。

对于固定铰，其运动约束为：

对于闭合铰，其运动约束为：

对于开放铰，其运动约束为：

式（7）～式（9）中：U1和 U2分别代表相邻模块车体在铰接关节处的平移运动；R1和R2分别代表转动运动；下标X、Y、Z代表平动或者转动的方向。

2.3 有限元模型建立及计算结果

复铰式五模块低地板车辆的有限元模型如图2所示，车体钢结构全部用相对等厚度的薄壳单元来模拟，车体上的大型设备及重要设备以集中质量的形式施加在各自的质心位置，不同模块之间的连接，用相应自由度的RJONT单元模拟。该有限元模型包含1 458 950个节点，1 761 221个单元。

▲图2 复铰式100%低地板车辆有限元模型

进行模态分析时，考虑到实际情况，在1、3、5模块的空簧底端施加约束，求解约束模态。通过计算，在刚体振型中，垂向振型主要有2个,第一个是模块1和模块2组合在一起的局部点头，第二个是模块3、模块4和模块5组合在一起的局部点头。车体侧滚振型有2个,分别是上心滚摆和下心滚摆。车体的横移和摇头振型共有5个：横向振型1表现为车体1、2与 3、4、5车反向摇头；横向振型2表现为车体1、车体5反向摇头,两悬浮车体也为反向摇头；横向振型3表现为各车体前后反向摇头；横向振型4表现为两悬浮车体同向摇头；横向振型5表现为两悬浮模块反向摇头。弹性振型中，整车振型的前三阶都为垂向振型，从第四阶开始为局部振型，图3为整车一阶垂弯。上述计算结果一同列入表1。

表1列举了整车的10种振型，此后的高阶振型主要是不同模块的局部弹性振动。与传统车辆相比，复铰式低地板有较高频率的局部点头振型，以及较低频率的车体一阶垂弯和二阶垂弯。根据车体动态设计准则，需要分析车体振型和转向架振动的耦合关系。

▲图3 整车一阶垂弯模态

▲图4 整车二阶垂弯模态

3 复铰式低地板车辆模态耦合分析

3.1 车体局部点头振动与构架浮沉振动的耦合关系

研究发现，模块2和模块3连接处的固定铰和开放铰都没有限制绕车体的点头自由度，它是引起复铰式低地板出现较大频率的局部点头振动的根源。如果该振型与转向架垂向振动产生耦合振动的话，会严重恶化模块2、模块3连接铰的受力情况，影响其使用寿命，并降低乘坐舒适性。因此，有必要分析该频率和转向架垂向振动的振幅和加速度倍率关系，表2为转向架的刚体垂向振动频率。

结合车辆的实际运营情况以及车体局部点头的振型。车体的局部点头振动应该与动力转向架的浮沉振动避开。根据动力学理论，当车体振动频率与转向架振动频率之比大于 2 时，才能起到有效隔振的效果。复铰式低地板车辆的局部点头频率小于转向架垂向振动的频率，为了保证车辆有良好的运行品质，就要使图5中的曲线都保持在低值且变化尽可能平缓。

表1 主要设计变量参数

表2 构架主要垂向振型频率/Hz

根据图（5）和图（6），强迫振动动力放大系数为

式中：ω为频率比；ζ为阻尼系数。

因此，车体局部点头振动的强迫振动放大系数为：

虽然车体局部点头振动与构架垂向振动的耦合会导致振幅增大，但是由图5可以看出，该数值在1附近，且在变化平滑区域。动力放大系数远小于1，振动的动力影响被削弱，因此，可以认为车体的局部点头振型与构架垂向振型不共振。

3.2 车体垂弯振动与转向架垂向振动耦合关系

▲图5 振幅扩大倍率与频率比关系

▲图6 加速度扩大倍率与频率比关系

▲图7 振幅扩大倍率与频率比关系

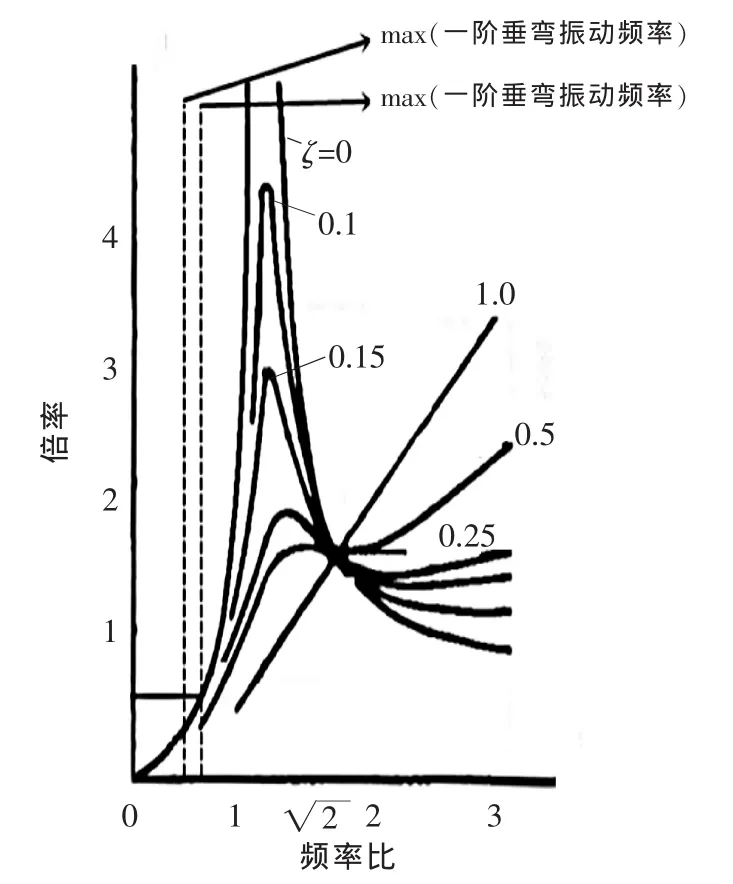
▲图8 加速度扩大倍率与频率比关系

车体的垂弯振动是车体动态设计中必须考虑的因素。如果车体低阶弹性振动频率与转向架刚体振动接近，就会使车体产生较大的振动，从而影响车辆结构的疲劳寿命和乘坐舒适度。我国在《高速试验列车动力车及动力学性能规范》中规定车体钢结构的一阶垂弯振动频率不得低于10 Hz，以避开转向架的浮沉振动，但复铰式低地板模态目前并没有相应的标准。同样，根据振动力学原理，提出只要垂弯振动与转向架浮沉振动的频率比能使振幅扩大倍率以及加速度扩大倍率都保持低值且在平缓变化区，就可以认为车体垂弯振型不会与构架浮沉振型产生共振。

图7和图8为某复铰式低地板车辆车体一阶垂弯频率与转向架构架主要垂向振动频率之间的振幅和加速度扩大倍率与频率比关系图。

根据式（11），车体垂弯产生的强迫振动放大系数为：