基于最小二乘支持向量机的MIMO线性参数变化模型辨识及预测控制

冯凯，卢建刚，陈金水

（浙江大学控制科学与工程学系工业控制技术国家重点实验室，浙江 杭州310027）

引 言

近年来，随着控制理论的发展，线性参数变化（linear parameter varying，LPV）模型系统辨识得到了学术界和工业界的广泛关注[1]。LPV这一名词，最先由Shamma等[2]在研究增益调度时提出，指的是一类状态依赖于某一可测调度变量的模型。

现有的线性参数变化模型根据模型结构进行划分，可分为基于传递函数的模型结构[3]，基于子空间的结构[4]和基于正交基的结构[5]。而基于输入输出传递函数的LPV模型结构大致又可分为2类：基于模型插值LPV结构和基于参数插值LPV结构。在基于模型插值的框架下，文献[6]提出了一种多模型线性参数变化架构。该算法首先选取几个典型工作点，并在典型工作点辨识得到系统的局部线性模型，然后根据工作点测试数据以及工作点间过渡数据，选取合适的权值插值函数，辨识出系统的全局模型。在基于参数插值的模型结构下，调度变量全局连续变化。假设模型系数可表示为一组基函数的线性组合，则系数可通过线性回归求解。两种方法各有优缺点，基于模型插值的LPV结构，典型工作点的选取主要依赖于经验，且合适的权值函数的选择也很关键，但该方法辨识成本较低，不会干扰正常工业过程；而基于参数插值的模型结构需要大范围进行测试，可能会干扰原系统正常运行，但该方法可通过线性回归的方法直接得到全局模型，计算量较低，模型结构更加紧凑。

传统的基于参数插值的LPV模型结构，模型质量与所选基函数密切相关。为了充分描述模型系数与调度变量的函数关系，通常会选取多于实际所需数目的基函数，这会导致严重的过参数化问题。而当系统先验知识不够时，往往又会因为基函数数目过少而导致模型结构偏差。

文献[7]针对单输入单输出系统提出了基于最小二乘支持向量机（least square support vector machine, LSSVM）的 LPV模型结构。LSSVM[8-9]由传统支持向量机发展而来，通过运用l2损失函数和线性回归，可得到问题的唯一解。相比传统SVM算法，LSSVM 算法通过线性回归求得唯一解，可大大减少计算量,这也为构建一种高效的 LPV辨识算法提供了可能。基于LSSVM-LPV模型可逼近复杂非线性系统，能自动决定模型结构，从而避免因基函数选择不当带来的模型结构偏差和方差过大等问题。本文将这一方法推广到多输入多输出（multiple-input multiple-output，MIMO）系统，仿真结果表明MIMO-LSSVM-LPV辨识算法能取得很好的辨识效果。

然后本文研究了基于MIMO-LSSVM-LPV模型结构的预测控制算法（model predictive control，MPC）。MPC因其能处理多输入多输出带约束问题得到了广泛关注[10]。大部分工业过程并不是严格的线性系统，这导致运用线性模型作为预测模型的方法并不是十分准确。而采用非线性模型作为预测模型又会导致最优控制量计算复杂，经典的数值计算方法无法得到最优解甚至可行解。遗传算法（genetic algorithm, GA）[11-12]作为一种非线性全局优化算法，具有简单通用、鲁棒性强、可并行处理等优点，很好地解决了以上问题。本文利用辨识所得的MIMO-LSSVM-LPV模型作为预测模型，在每个采样点预测系统输出，结合遗传算法，实时滚动优化控制量，取得了很好的控制效果。

1 ARX模型的LPV辨识[7]

给定单输入单输出离散时间系统的有源自回归模型（auto-regressive model with exogenous input，ARX）如下

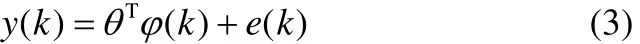
假设样本数据集为

对式( 3 )的最小二乘估计可表示为

从而问题(5)的最优解可表示为

2 基于MIMO-LSSVM-LPV模型辨识

与第 1节介绍的标准最小二乘不同，在基于LSSVM-LPV模型结构辨识算法中，系数iφ与p的函数依赖关系未知。文献[7]已证明，在函数依赖关系未知的情况下，基于LSSVM-LPV模型辨识算法可以得到一致估计。为实现该方法在多输入多输出系统的应用，系统的每一个输出需分别独立进行辨识。为了简化过程，文中以2输入2输出系统为例。记参数化模型结构为

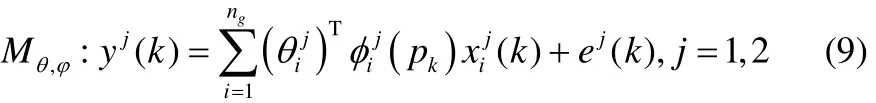
式中，j代表系统第j个输出，代表具体形式未知的特征映射模型。是第i个参数向量，是模型j的预测误差。定义(k)为

记

则式(9)可表示成如下形式

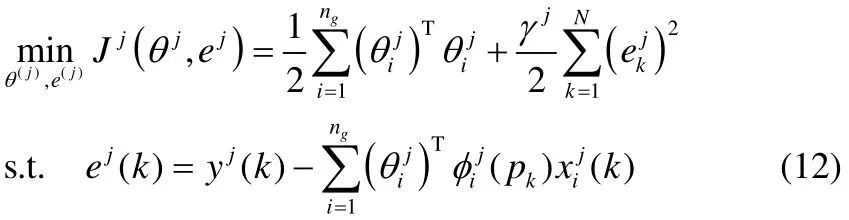
式中，是调节参数，是最小化训练误差和模型复杂度之间的折中，对 LPV 模型的推广性能有着重要影响。该带约束优化问题可通过构造拉格朗日函数在对偶空间求解。

将式(14)、式(15)代入式(16)，可得

式中，k∈ { 1,… ,N}，N代表样本数目。式(17)可进一步表示为

且

式中，Ki是人们熟知的核函数，通过将高维空间的点积运算转化为原输入空间的代数运算，极大地简化了计算。也使得问题的求解不再需要确定的具体形式，只需选择合适的核函数即可。常用的核函数有径向基核函数（radial basis function，RBF）、多项式核函数等。这里采用常用的 RBF，定义如下

其中，是输出的平均值，是根据辨识出的模型的预测值。采用核函数，式(18)的解可表示为

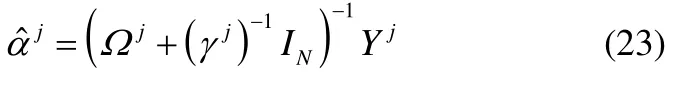
在该算法中，作为中间变量，它的值无法直接求解。通过运用核函数，该方法能得到以系数()T(·)为整体的值。利用得到的，即可根i据式(11)求得模型的预测输出。

3 基于MIMO-LSSVM-LPV模型预测控制研究

预测控制是基于模型的先进控制算法。根据历史信息及未来输入，利用模型预测未来输出，通过对某个性能指标最优化计算确定当前控制时域内最优控制序列[13]。通常只将当前时刻最优控制量作用于系统，并在下一时刻重复上述过程，故称为有限时域滚动优化。预测模型只强调功能不强调结构。对一R输入Q输出带约束系统，性能指标通常为

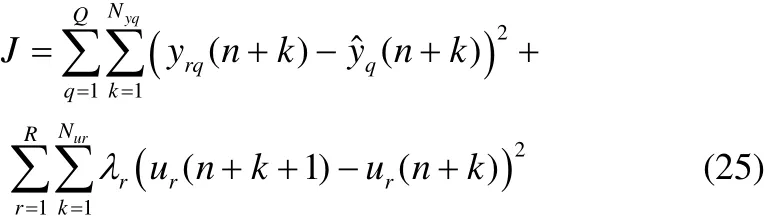
其中系统约束为

式中，Nur为第r个输入的控制时域，Nyq为第q个输出的预测时域，rλ为调节系数，yrq和yˆq分别是第q个输出的实际值和预测值，urh和url分别是第r个输入的上下限。利用辨识所得的MIMO-LSSVM-LPV模型作为预测模型，根据当前所处工况点，根据式(24)计算辨识所得系数，再利用式(11)即可得到模型预测输出。利用遗传算法的全局搜索特性计算满足约束且使性能指标式(25)最优的控制序列。将当前最优控制量作用于系统，并在每个采样点重复上述过程，即可实现过程的控制。具体的算法框图见图1。

图1 预测控制结合遗传算法框图Fig.1 Block diagram of GA based MPC

4 辨识研究

4.1 实例一：LPV-ARX模型辨识

设有如式(27)的双输入双输出LPV系统

其中调度变量P∈[−1 ,1]，e为零均值随机噪声过程 ，系统系数如式(28)所示。

在该系统中，模型系数对调度变量p为静态依赖，但是系数非线性情况复杂，用传统的非线性辨识方法很难得到满意的解。

将对式(27)的辨识问题转化为对如下模型结构的辨识

选取

，的选取并不需要完全一致，具体情况需视辨识系统而定。调度变量p的操作轨迹按照p(k)= sin(0.25k)变化。用幅值在[−1,1]之间零均值均匀分布的随机数作为系统输入u1,u2，产生 2000组输入输出序列。其中，1500组用于辨识，500组用于测试。首先在无噪声条件下测试算法性能。通过网格法，最大化BFR，得核函数中待整定参数为运用基于MIMO-LSSVM-LPV辨识算法对该系统进行辨识，系数的辨识结果如图 2。由图 2可知，在没有系统先验知识的情况下，该算法可以很好地辨识出非线性特性严重的系统参数。

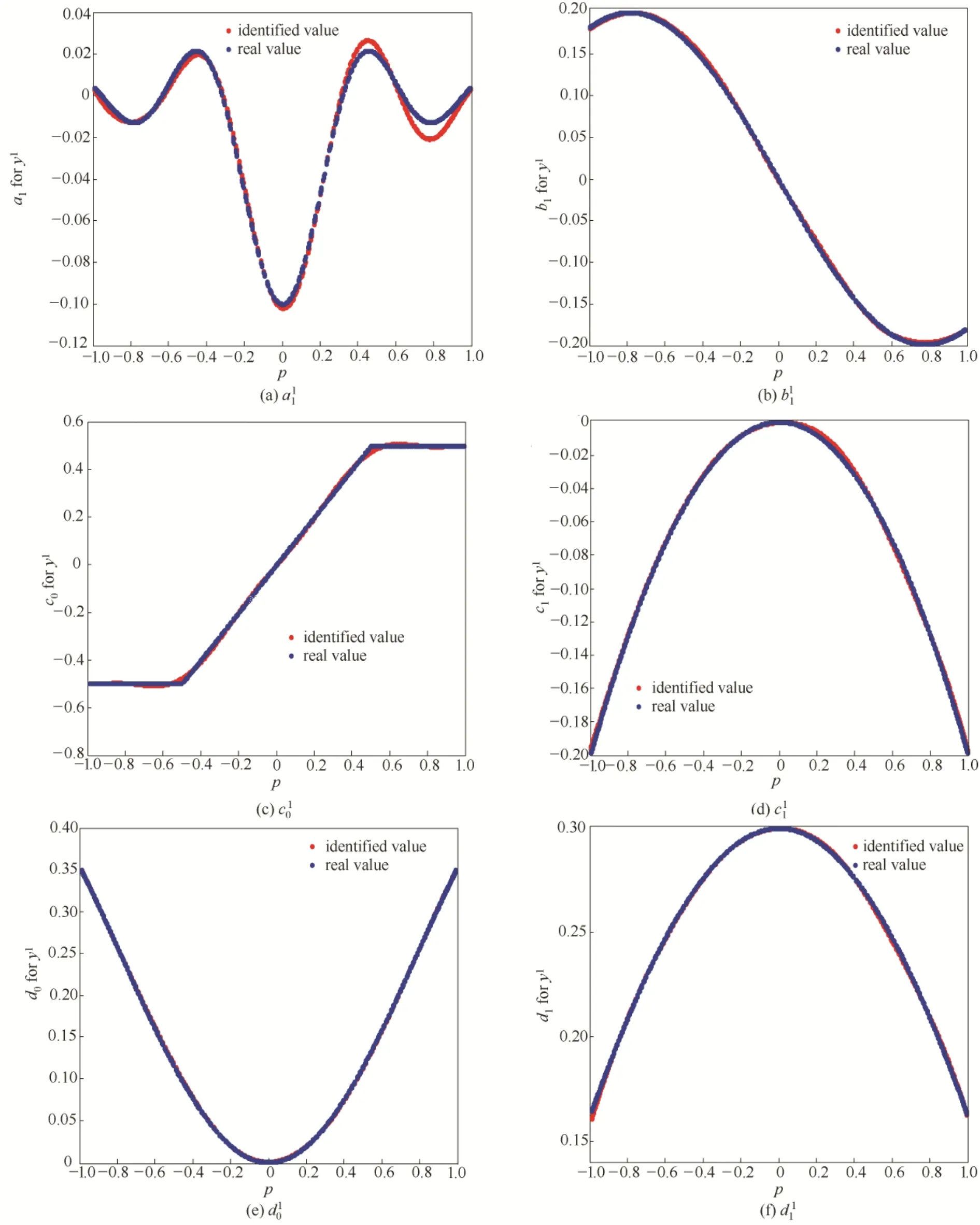
图2 LPV模型参数估计Fig.2 Identified parameters of LPV models

定义输出误差为

图3 辨识模型输出和实际系统输出比较Fig.3 Comparison between identified outputs and actual outputs

对测试集进行预测，预测效果如图3。从图3可以看出，运用基于MIMO-LSSVM-LPV辨识算法辨识得到的模型输出能很好地跟踪原系统的输出，1y，y2的输出误差如表1所示，可见该辨识算法辨识的模型准确度很高。

表1 输出误差Table 1 Output error

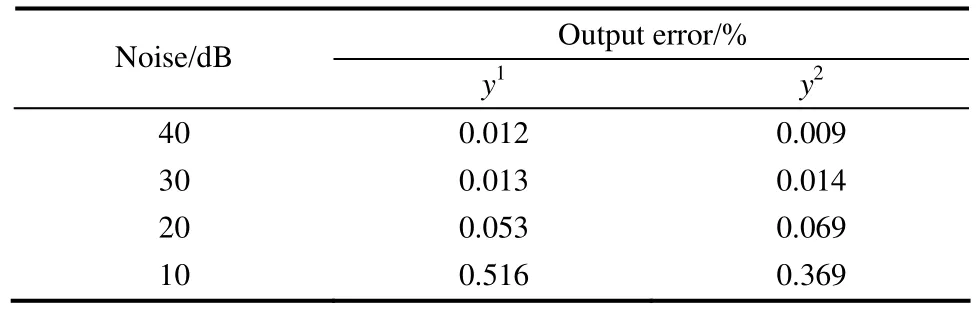
表2 不同噪声水平下系统输出误差Table 2 Output error under different noise

4.2 实例二：等温型CSTR模型辨识

连续搅拌釜反应器（CSTR）[14]是生产聚合物时使用最广泛的反应器。该反应是典型的多工况过程[15-16]。本文选用文献[17]中提出的理想的 CSTR过程模型为研究对象。该过程代表等温伪一阶反应A+B→P反应过程，其中反应物A浓度过量。过程模型可表示为

约束条件为

参数取自文献[18]

该过程为典型的双输入双输出系统，两个输入为u1和u2，两个输出为y1和y2，是一个有上下界约束的非线性多输入多输出系统。取输入向量为

图4 预测模型输出和实际系统输出比较Fig.4 Comparison between predicted outputs and actual outputs

图5 预测控制输出及控制量变化Fig.5 Predicted outputs and control actions

输出为y1和y2，u2为调度变量。为充分激发系统非线性，u1和u2采用零阶保持信号，并分别按照正弦和余弦函数变化。单个信号持续作用时间为300 s，采样周期为 2 s。共产生数据 7500组，其中 5000组用于辨识模型，2500组用于验证模型效果。在无噪声情况下进行辨识，通过最大化BFR，得到待整定参数为σ1=0.1，σ2= 0 .1，γ1=1，γ2=1 。辨识所得两个MISO模型，仿真效果如图4所示，可见模型能很好地逼近系统的非线性。

5 预测控制研究

针对式(27)和式(28)代表的非线性过程，利用已经辨识得到的MIMO-LSSVM-LPV模型作为预测模型，开展系统预测控制研究。设定系统初值为y1=0，y2=0。GA 使用二进制编码，初始种群大小为 30，最大迭代次数 200，交叉概率 0.7，变异概率 0.1，适应度函数为预测控制算法性能指标[式(25)]的倒数。预测控制算法的预测时域和控制时域都为2。为了测试算法在不同工作点间切换性能,令调度变量在时刻50及100时分别从0.8变化到0.9再变到1.0，系统的输出及控制作用如图5所示。由图5可知，当工作点发生切换时，该控制算法能很快使系统输出达到并稳定在设定值附近。同时，基于GA的预测控制计算单步最优控制量的时间仅为0.75 s，完全能够实现在线计算。

6 结 论

本文结合针对多输入多输出系统的最小二乘支持向量机线性参数变化模型的辨识算法及基于遗传算法的预测控制算法，提出了MIMO-LSSVMLPV+GA-MPC辨识及控制一体化架构。MIMOLSSVM-LPV辨识算法能自动判断模型结构，避免了因基函数选择不当带来的模型失配。两个仿真实例表明，该算法能逼近复杂非线性系统，且计算量低。结合遗传算法的预测控制可以使系统在不同工作点间切换时快速达到控制目标。但是该辨识算法对噪声比较敏感，通过网格法选取最优整定参数费时过长，未来研究可着重针对这两方面。

[1]Yu Zhao, Huang Biao, Su Hongye, Chu Jian. Prediction error method for identification of LPV models [J].Journal of Process Control,2012, 22 (1): 180-193

[2]Shamma Jeff S, Michael Athans. Analysis of gain scheduled control for nonlinear plants [J].Automatic Control, IEEE Transactions on,1990, 35 (8): 898-907

[3]Previdi F, Lovera M. Identification of a class of non-linear parametrically varying models [J].International Journal of Adaptive Control and Signal Processing, 2003, 17 (1): 33-50

[4]Verdult Vincent, Michel Verhaegen. Subspace identification of multivariable linear parameter-varying systems [J].Automatica, 2002,38 (5): 805-814

[5]Tóth Roland, Peter S C Heuberger, Paul M J Van den Hof.Asymptotically optimal orthonormal basis functions for LPV system identification [J].Automatica, 2009, 45 (6): 1359-1370

[6]Zhu Y C, Xu Z H. A method of LPV model identification for control//Proceedings of 17th IFAC World Congress [C]. Seoul, Korea,2008

[7]Tóth Roland, Vincent Laurain, Wei Xing Zheng, Kameshwar Poolla.Model structure learning: a support vector machine approach for LPV linear-regression models//50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC)[C]. 2011:3192-3197

[8]Suykens Johan A K, Joos Vandewalle. Least squares support vector machine classifiers [J].Neural Processing Letters, 1999, 9 (3):293-300

[9]Wang Haifeng, Hu Dejin. Comparison of SVM and LS-SVM for regression//International Conference on Neural Networks and Brain.ICNN&B’05 [C]. 2005: 279-283

[10]Li Ping (李平), Ren Penghui (任朋辉). Multiple constrained generalized predictive control for cascade industrial systems [J].CIESCJournal(化工学报), 2010, 61 (8): 2159-2164

[11]Davis Lawrence. Handbook of Genetic Algorithms[M]. New York:Van Nostrand Reinhold, 1991

[12]Whitley Darrell. A genetic algorithm tutorial [J].Statistics and Computing, 1994, 4 (2): 65-85

[13]Qian Jixin (钱积新), Zhao Jun (赵均), Xu Zuhua (徐祖华).Predictive Control (预测控制)[M]. Beijing: Chemical Industry Press,2007

[14]Luo Xionglin (罗雄麟), Yu Yang (于洋), Xu Jun (许鋆). Online optimization implementation on model predictive control in chemical process [J].CIESC Journal(化工学报), 2014, 65 (10): 3984-3992

[15]Jie You, Yang Qinmin, Lu Jiangang, Sun Youxian. Identification of LPV models with non-uniformly spaced operating points by using asymmetric gaussian weights [J].Chinese Journal of Chemical Engineering, 2014, 22 (7): 795-798

[16]Ge Zhiqiang (葛志强), Song Zhihuan (宋执环). New online monitoring method for multiple operating modes process [J].Journal of Chemical Industry and Engineering(China)(化工学报), 2008, 59(1): 135-141

[17]Oliveira N M C. Newton-type algorithms for nonlinear constrained chemical process control [D]. Pittsburgh: Carnegie Mellon University,1994

[18]Martinsen F, Biegler L T, Foss B A. A new optimization algorithm with application to nonlinear MPC [J].Modeling Identification and Control, 2005, 26 (1): 3-22