水泥生料立磨粉磨生产过程的ELM模型

林小峰 梁金波

(广西大学电气工程学院，广西 南宁 530004)

水泥生料立磨粉磨生产过程的ELM模型

林小峰 梁金波

(广西大学电气工程学院，广西 南宁 530004)

为了降低水泥生料立磨粉磨生产过程的能耗，提高系统的稳定性和生产效率，提出了采用极限学习机网络建立水泥生料立磨粉磨生产过程的生产指标预测模型。结合某水泥厂水泥生料立磨粉磨生产过程的实测参数数据，对模型进行了训练和测试。试验结果表明，该建模方法实现了立磨粉磨过程关键指标参数的在线预估，对立磨生料粉磨生产过程中相关参数的优化设定和降低生产过程的能耗具有一定的参考意义。

立磨 粉磨 极限学习机 数据处理 预测

0 引言

立磨作为现代新型干法水泥生料粉磨生产过程的首选设备，集破碎、烘干、粉磨、选粉、输送功能于一体[1]。水泥生料立磨粉磨是水泥生产过程的重要生产环节和典型耗能环节。据统计，其粉磨生产过程的电耗占整个水泥生产电耗的75%[2-3]。水泥生料立磨粉磨生产过程具有多变量、非线性、强耦合等特点，难以建立精确的数学模型[4]，且关键参数指标无法在线测量，参数的设定值主要依靠操作人员的人工经验手动调节，使水泥生料立磨粉磨生产过程具有很大的主观性与滞后性。

客观及时地自动调节各工艺指标参数，降低水泥生料立磨粉磨生产过程的能耗，提高生产过程的稳定性和生产效率，实现水泥生料粉磨生产过程的最优控制是目前亟待解决的问题。

随着智能控制的发展以及一些复杂生产过程的实际控制要求，神经网络技术也得到不断发展，其研究领域涉及石油、化工和环保等诸多领域。由于前向神经网络的种种优良特性，使得它在软测量建模领域中有着非常广泛的应用[5]。然而，传统的学习算法存在速度较慢、求解过程易陷入局部极小问题等。

极限学习机(extreme learning machine，ELM)是Huang等人在2006年首次提出的一种新型单隐藏层前馈神经网络的学习方法。该方法避免了基于梯度下降学习方法存在的一些问题，如落入局部最小点、迭代次数多以及学习率的设定问题等，在保证网络具有良好的泛化性能的同时，极大地提高了前向神经网络的学习速度。

本文通过分析水泥生料立磨粉磨生产过程中各变量之间的耦合关系，利用极限学习机建立其粉磨生产过程的关键指标的预测模型。结合某水泥厂水泥生料立磨粉磨工艺过程的实测参数数据，对该模型进行训练和测试，使网络模型能够根据某时刻的输入信息直接计算出下一时刻需要测量的指标值。

1 生料立磨粉磨工艺流程

水泥生料立磨粉磨流程主要分为粉磨和选粉两个阶段。在粉磨阶段，通过喂料皮带机将混合原料输送到磨机的喂料口，物料沿喂料管道进入立磨机内部，落入旋转磨盘平面中心；然后，在物料间的推力作用和离心力作用下，移动到磨辊和磨盘之间的研磨层粉磨。在选粉阶段，物料经磨辊研磨后，继续运动直到离开磨盘边缘遇到通过风环进入磨机内的热气体；粗粉落入磨机底部，通过外循环再次进入磨机粉磨；细粉被风环处高速气流吹起，经过分离器选粉，不合格的细粉落到磨盘继续粉磨，合格的细粉随气流排出立磨机，再经过旋风分离器细选，达到要求的细粉由收尘器收集为成品[6]。

生料立磨粉磨工艺流程如图1所示。

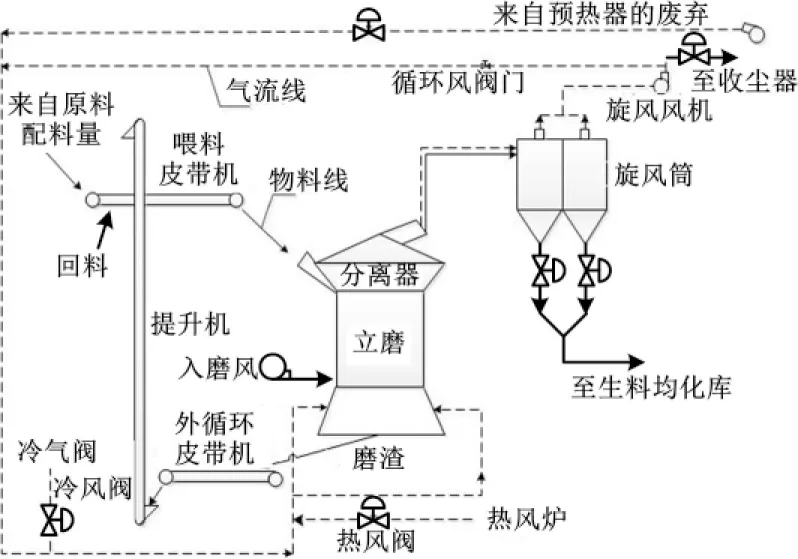
图1 生料立磨粉磨工艺流程图

在生料粉磨生产过程中，针对物料和设备运行参数的变化适时进行调节控制，是确保系统稳定运行的关键环节。影响系统稳定运行的主要因素[7-8]如下。

① 喂料量。稳定的喂料量是确保磨机内压差的前提条件，并且是一个非常重要的调节变量。当喂料量不足时，磨盘上的料层变得不稳定，如果风量一定，那么磨机内压差会降低。当喂料量过少，容易导致立磨机的振动跳停；当喂料量过大时，磨盘上会出现“犁料”现象。料层同样难以稳定，过多的物料，不仅容易导致“饱磨”，而且会使磨机内压差升高。

② 入磨机风温。入磨机风温会对磨机内风量和压差造成一定影响。入磨机风温度高，会使物料变得松散，使料层变薄，回料量上升，磨机内压差也相应增大；入磨机风温度过低，物料含水量大，粉磨和选粉效率都会降低，磨机内压差也相应降低，使产量受到影响。

③ 研磨压力。过小的研磨压力不能充分细磨物料，使吐渣量增多、压力增大；粉磨效率虽高，但功率消耗也增大，易引起振动。

④ 分离器转速。分离器的转速将直接影响生料细度指标，而生料细度指标是选粉阶段非常重要的监测指标。选粉机转速过大或过小都会直接影响最终收集的生料粉磨颗粒的质量。

⑤ 循环风阀门开度。风量的大小也将直接影响生料细度指标。磨内风量的调节一般是通过控制循环风阀门开度来实现的。如果在风压不变的条件下，磨机内风量较大，会使磨内粉尘浓度变小，降低磨机内压差。风量大、风速快会使更多的粉尘通过选粉机，造成生料细度值增大。

综上可知，整个生产过程中的多种变量相互影响，主要参数之间带有很强的耦合性。对立磨生料粉磨生产过程来讲，反映其过程好坏的两个最主要评价指标是磨机内压差和生料细度。在实际生产中，磨机内压差是磨机运行状态好坏的核心判断指标，而生料细度的大小将直接影响后续水泥的煅烧。影响水泥生料细度和磨机内部压差这两个关键指标的因素主要是喂料量、入磨机风温度、研磨压力、分离器转速和循环风阀门开度。

2 模型建立

2.1 极限学习机

极限学习机(ELM)的网络拓扑结构如图2所示。

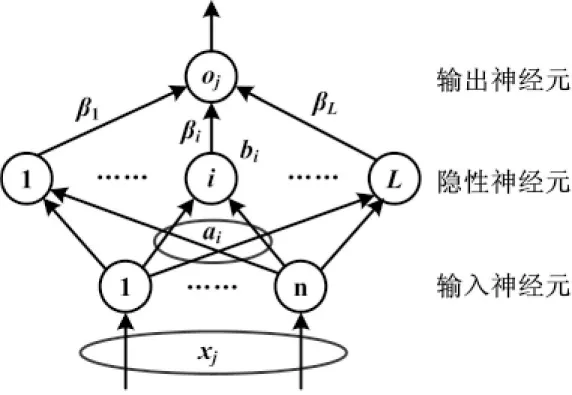
图2 ELM神经网络结构图

图2中，ai、bi为隐藏层神经元节点参数；β1、βi、βL为隐藏层神经元输出权值，L为隐藏层神经元个数；xj(j∈1,...，n)为输入神经元个数；oj(j∈1,...，n)为输出神经元个数[9]。

ELM的核心学习方法如下。

② 随机选取输入权值向量和隐藏层神经元节点阈值ai,bi,i=1,…,L；

③ 计算隐藏层节点输出矩阵H=g(a,b,x)；

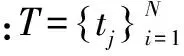
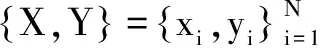
一般来说，ELM模型的训练过程包括两部分。第一部分是确定隐藏层节点的数量，第二部分是计算隐藏层输出权值。其传递函数可以是任意非线性分段连续的函数，例如下面的S函数和高斯函数等。

① S型函数：

(1)

② 高斯函数：

g(x;θ)=exp(-b‖x-a‖)

(2)

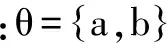
ELM方法的一个重要特点是隐藏层映射函数的参数可以根据在区间(-1,1)之间的连续概率分布自由选择。人工给定模型网络的隐藏层节点个数，模型唯一需要确定的是隐藏层神经元到输出神经元之间的权值。那么，ELM的训练过程就转换为解决一个最小二乘的问题。

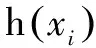
(3)

然后，通过最小化预测误差的平方误差之和得到输出权值，公式为：

(4)

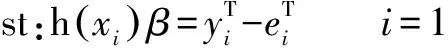
式中：ei∈Rno为第i个训练样本的误差向量；C为对训练误差的一个影响因子。

通过取代目标函数的约束，得到以下无约束的求最优解问题：

(5)

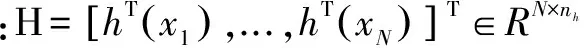
以上问题就是我们熟知的正则化最小二乘法。通过设置LELM从β到0的梯度，得到以下公式：

(6)

如果H的行数大于列数并且是列满秩，即训练样本的个数大于隐层神经元个数，那么:

(7)

式中：Inh为nh维单位矩阵。

需要注意的是，在式(7)的实际计算过程中，可以用高斯消元法简化求矩阵的逆阵，这样可以使解线性方程的过程更高效、更稳定。

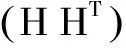
(8)

(9)

式中：IN为一个N维的单位矩阵。

因此，在训练样本大于隐藏层神经元个数时，用式(7)来得到输出权值，否则用式(9)计算。

2.2 数据预处理

根据某水泥厂5 000t/d生产线中生料生产过程采集数据并记录，这些数据包含在线记录和离线化验数据。在线数据是控制站监控软件实时记录的数据，包括操作变量、工况等实时数据；离线数据是化验室人员通过现场采集样本化验分析的结果，主要是生料细度指标。从实际粉磨生产过程中采集到的原始数据不能直接使用，必须进行预处理。这是因为，一方面，数据需要按时间进行匹配。由于在线和离线数据采样时间不同，离线参数指标生料细度的抽样化验周期为1h，而在线数据采集周期为1min，因此需要对采集到的数据进行时间匹配。以离线数据的记录时间作为标准，找出时间匹配的在线数据进行组合。另一方面，这些原始数据含有人为因素造成的主观误差，以及因测量信号受噪声污染产生的随机误差。这些都会使所建模型与实际过程不符导致生产指标预测不准确。

在数据预处理过程中，首先应消除主观误差，根据实际生产中变量的操作范围，采用限幅的方法剔除不在范围内的数据，当数据样本与总体平均值的偏差大于3倍标准差时就剔除该组数据。其次，降低随机误差。采用七点线性平滑法对数据进行平滑处理，消除随机噪声。这种方法作为一种数据补救措施是对原始数据进行填充和平滑。最后，采用主成分分析法对数据进行压缩和降维。算法如下。

① 对于n维随机向量x=(x1,x2,…,xn)T，原始数据标准化如下。

(10)

(11)

(12)

② 计算相关矩阵R：

(13)

式中：X*为标准化后的数据矩阵；X*T为X*的转置矩阵。

③ 计算相关矩阵R的特征值λi和相应的正交单位特征向量，主成分的方差贡献率即为：

(14)

方差积累贡献率如下：

(15)

④ 最后，根据方差积累贡献率大于85%的原则，确定选择的主成分个数。

经过预处理，获得450组有效数据，部分数据如表1所示。其中，在线指标包括喂料量、选粉机转速、循环风阀门开度、入磨风温和磨机内压差，离线数据是生料细度指标。

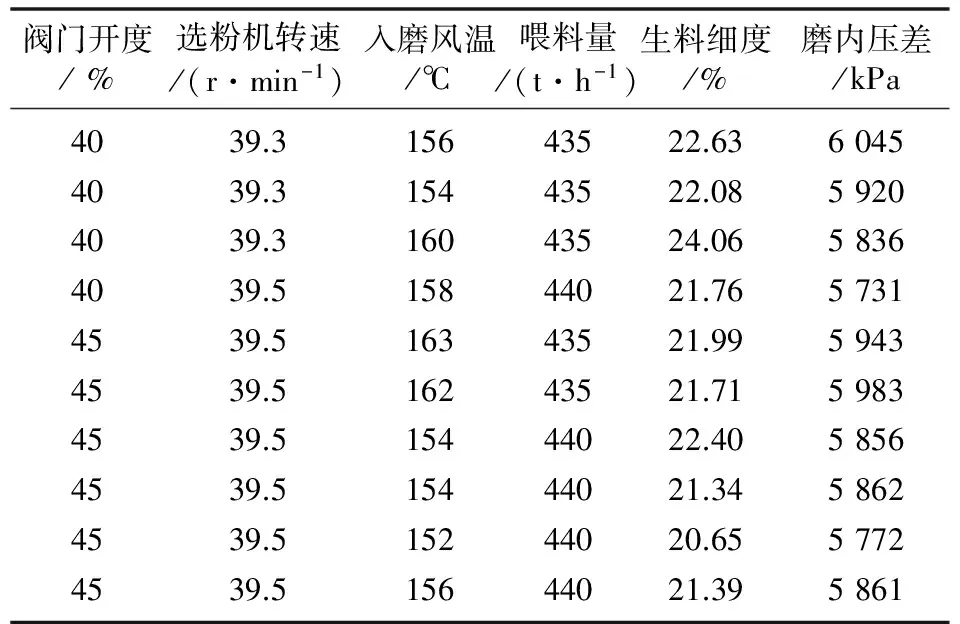
表1 水泥厂生料生产过程部分数据

3 模型仿真及结果分析

将450组数据按8∶1的比例分为训练数据集和测试数据集,其中训练数据400组，测试数据50组。每组数据集包含6个数据。前面4个数据作为网络模型的输入变量，它们代表的物理意义分别为循环风阀门的开度x1、分离器的转速x2、入磨机风的温度x3和磨机的喂料量x4；后面2个数据作为网络模型的输出，它们代表的物理意义分别为生料细度y1和立磨机内的压差y2。

采用基于ELM方法的立磨粉磨生产过程的神经网络预测模型，模型基本结构为单隐藏层结构。网络初始化后设置的相关参数如下：模型的输入为4个节点，输出为2个节点，网络模型的隐藏层节点参数为50个，循环次数为1次。将400组训练数据代入ELM模型进行训练，训练完成后再将50组测试数据代入模型进行测试，得到模型输出的2个指标泛化曲线分别如图3、图4所示。

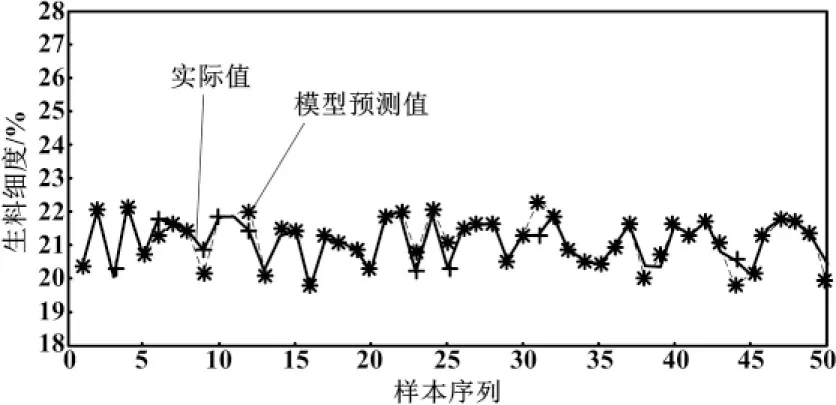
图3 基于ELM的生料细度预测曲线

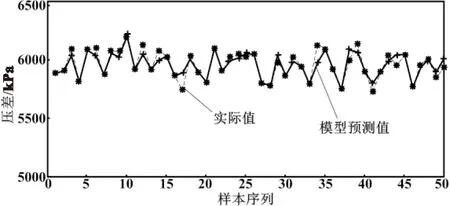
图4 基于ELM的磨内压差预测曲线

采用相同方法，建立BP神经网络预测模型，该模型为单隐藏层结构。网络初始化后，设置网络的相关参数如下：网络的隐藏层节点个数为50，输入神经元为4个，输出神经元为2个，网络的学习速率为0.01，误差精度为0.05，最大训练次数为2 000次。BP神经网络预测模型与ELM模型仿真结果的比较如表2所示。

表2 ELM与BP的模型性能比较

从表2可以看出，在保证网络模型具有一定的预测误差前提下，基于ELM方法的指标预测模型相比BP模型的学习速度快，经过的迭代次数少，训练时间短。

4 结束语

本文针对水泥生料立磨粉磨生产过程的高能耗、难以在线监测生料细度指标以及人工设定参数存在的问题，提出了基于极限学习机学习方法，建立了生料立磨粉磨生产过程的指标预测模型。结合模型，利用某水泥厂水泥生料立磨粉磨生产过程各变量的在线记录和离线化验所得的数据对模型训练和测试。实验结果验证了该方法是有效的， ELM模型能够反映水泥生料立磨粉磨生产过程的关键工艺指标之间的映射关系。该方法在保证较小误差的情况下，具有更快的在线预估速度，对降低立磨粉磨生产过程的电耗具有一定的参考意义。

[1] 肖争鸣，李坚利.水泥工艺技术[M].北京:化学工业出版社，2006:65-76.

[2] Ajaya K P,Hare K M.A hybrid soft sensing approach of a cement mill using principal component analysis and artificial neural networks[C]//2013 IEEE International Advance Computing Conference,2013：713-718.

[3] Ajaya K P,Hare K M.Soft sensing of particle size in a grinding process:application of support vector regression,fuzzy inference and adaptive neuro fuzzy inference techniques for online monitoring of cement fineness[J].Powder Technology,2014(264):484-497.

[4] 秦伟，颜文俊.水泥立磨流程的建模和控制优化[J].控制工程，2012,19(6):929-943.

[5] 刘晴，张正则，丁维明.神经网络预测PID控制在气化炉中的应用[J].自动化仪表，2014,35(5):60-62.

[6] 贾华平.水泥粉磨新型节能工艺的发展现状[J].四川水泥，2014(3)：106-112.

[7] 周正立，周君玉.水泥粉磨工艺与设备问答[M].北京：化学工业出版社，2009:70-77.

[8] 苑明哲，王卓，宁艳艳.水泥生料立磨压差广义预测PID控制[J].信息与控制，2012,41(3):378-390.

[9] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006，70(3):489-501.

[10]Huang G,Jatinder N D,Song S J.Semi-supervised and unsupervised extreme learning machines[C]//2014 IEEE Transactions on Cybernetics,2014:2405-2417.

ELM Model of Cement Raw Material Vertical Mill Grinding Production Process

In order to reduce the energy consumption in cement raw material vertical mill grinding production process, and enhance the stability of the system and the production efficiency, it is proposed that by adopting extreme learning machine (ELM) network to establish the prediction model of production quotas for such process. Combining with the measured parameteric data of the process in certain cement plant, the model is trained and tested. The experimental results show that the modeling method proposed is effective for implementing online preditive estimation of critical parameters for vertical mill grinding process, in addition, it posseses certain reference significance for optimizing the parameters for raw material veritical mill grinding process and reducing energy consumption of the production process.

Vertical mill Powder grinding Extreme learning machine Data processing Prediction

国家自然科学基金重点资助项目(编号：61034002)；

国家自然科学基金资助项目(编号：61364007)。

林小峰(1955-)，男，1979年毕业于广西大学电气工程专业，获学士学位，教授；主要从事复杂系统智能控制与优化、过程控制、计算机控制、电工新技术、新能源转换与控制等方面的研究。

TH89;TP29

A

10.16086/j.cnki.issn1000-0380.201509002

修改稿收到日期：2015-01-14。